Bekanntschaft mit dem einfachsten neuronalen Netz und dessen schrittweise Implementierung

Einmal stieß ich auf ein Buch mit dem Titel "Create Your Neural Network" , das von Tarik Rashid verfasst wurde. Im Gegensatz zu vielen anderen Büchern über neuronale Netze wurde hier alles in einfacher Sprache mit einer ausreichenden Anzahl von Beispielen und Tipps präsentiert

Inspiriert von diesem Buch möchte ich es Schritt für Schritt durchgehen - nämlich seinen praktischen Teil - das Schreiben von Code für das einfachste neuronale Netzwerk .
Dieser Artikel richtet sich an diejenigen, die neuronale Netze und maschinelles Lernen betreiben möchten, aber bisher Schwierigkeiten haben, diesen erstaunlichen Bereich der Wissenschaft zu verstehen. Das einfachste Gerüst des Codes eines neuronalen Netzwerks wird nachstehend beschrieben, so dass viele das einfachste Prinzip der Konstruktion und Interaktion von allem verstehen, woraus dieses neuronale Netzwerk besteht.




Theorien zum maschinellen Lernen und zu neuronalen Netzen am Habré reichen aus. Aber wenn jemand es braucht, werde ich am Ende des Artikels einige Links hinterlassen. Und jetzt beginnen wir direkt mit dem Schreiben von Code und schreiben in Python . Ich empfehle die Verwendung von Jupyter-Notebook beim Schreiben von Code

Schritt 1. Netzwerkinitialisierung

Zunächst müssen wir natürlich alle aktiven Komponenten unseres Netzwerks initialisieren

# numpy —    Python,        import numpy #  scipy.special , -scipy    , ,  ,      ,       ,   - " " import scipy.special #,      import matplotlib.pyplot #     class neuralNetwork: #     def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #     ,   ,   ,  ) #     ,  ,   self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #    , wih -       ,    who-       self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) #   -  ,  ,  ,    ,     ,     ,  ,  ,   self.lr = learningrate #  -   self.activation_function = lambda x: scipy.special.expit(x) 

Sigmoid

Diese Funktion gehört zur Klasse der stetigen Funktionen, nimmt am Eingang eine beliebige reelle Zahl (d. H. Nicht unbedingt eine ganze Zahl) und gibt am Ausgang eine reelle Zahl im Bereich von 0 bis 1 an .

Insbesondere werden große (Modulo) negative Zahlen zu Null und große positive Zahlen zu Eins .

Seine Ausgabe wird gut als Grad der Neuronenaktivierung interpretiert: von der Abwesenheit der Aktivierung (0) bis zur vollständig gesättigten Aktivierung (1).

Das Sigmoid wird durch die Formel ausgedrückt:



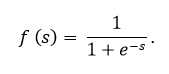
Das Diagramm der Sigmoidfunktion gemäß der folgenden Abbildung:



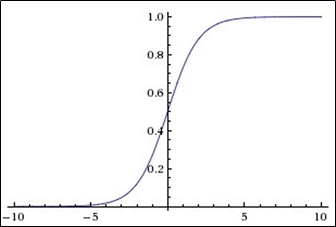
Die Sigmoidfunktion ist:

• kontinuierlich
• monoton ansteigend;
• differenzierbar.

In diesem Code ist das Sigmoid, wie Sie sehen können, unter dem Namen expit (x) vorhanden.

Ein bisschen darüber, wie ein Knoten in einem neuronalen Netzwerk aussieht

Das Bild zeigt am meisten diesen Knoten, nur wird er normalerweise in Form eines Kreises und nicht eines Rechtecks ​​dargestellt. Wie wir sehen, gibt es innerhalb eines Rechtecks ​​(Brunnen oder eines Kreises) - das ist alles abstrakt - zwei Funktionen:

Die 1. Funktion beschäftigt sich mit der Tatsache, dass sie alle Eingaben unter Berücksichtigung der Gewichte, Daten und manchmal sogar unter Berücksichtigung des Verschiebungsneurons empfängt (ein spezielles Neuron, das es den Graphen einfach ermöglicht, sich zu bewegen und sich nicht zu einem hässlichen Haufen zu vermischen, das ist alles).

Die 2. Funktion nimmt als Parameter denselben Wert an, den die erste Funktion summiert hat, und diese zweite Funktion wird als Aktivierungsfunktion bezeichnet. In unserem Fall ein Sigmoid

Wir fahren fort :

Teil 2. Neuronales Netzwerktraining

 def train(self, inputs_list, targets_list): #       inputs = numpy.array(inputs_list, ndmin=2).T #     input targets = numpy.array(targets_list, ndmin=2).T #  targets #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,       .    ,       hidden_inputs (1 ),        -   (2 ) hidden_outputs = self.activation_function(hidden_inputs) #    ()  final_inputs = numpy.dot(self.who, hidden_outputs) #  ,     final_outputs = self.activation_function(final_inputs) #   ( - ) output_errors = targets - final_outputs #      ,    <b>  </b>,   <b>       </b>(      ) hidden_errors = numpy.dot(self.who.T, output_errors) #        ( ,      ) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) #       (       ) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

Und jetzt nähern wir uns dem Ende

Teil 3. Abfrage eines neuronalen Netzes

 #  ,      def query(self, inputs_list): #         inputs = numpy.array(inputs_list, ndmin=2).T #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,     hidden_outputs = self.activation_function(hidden_inputs) #      final_inputs = numpy.dot(self.who, hidden_outputs) #     ,     final_outputs = self.activation_function(final_inputs) return final_outputs 

Wir bringen es zum Ende

 #     ,  ,  (  <b></b>-    , ,   input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #    -   , ... 0.3! learning_rate = 0.3 #   (n    neuralNetwork ,      __init__ ,        n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate) 

PS

Oben wurde ein rechnerisch einfachstes Modell eines neuronalen Netzwerks vorgestellt. Es wurde jedoch keine spezifische Anwendung gezeigt.

Wenn Sie möchten, können Sie noch weiter gehen, indem Sie die Fähigkeit hinzufügen, handgeschriebenen Text im MNIST- Code zu erkennen. Dazu können Sie mit dieser Jupyter-Datei vollständig herausfinden (und einfach Spaß haben). Meine Aufgabe war es, den Code zu demonstrieren und, wenn möglich, im Netzwerk und für zu kauen welche Antworten

PPS

Nachfolgend finden Sie nützliche Links:

1. Link zu Github Tarik ->
2. Sein Buch ->
3.Maschinelle Lerntheorie ->
4.Maschinelle Lerntheorie ->
5.Maschinelle Lerntheorie ->