Zero-Knowledge-Beweise / Argumente sind eine aufkommende kryptografische Technologie, die verspricht, uns dem Heiligen Gral der Blockchain näher zu bringen: Datenschutz und Überprüfbarkeit.
Mögliche Anwendungen für Nullwissen umfassen, sind aber nicht beschränkt auf:
Eine weitere Anwendung für wissensfreie Beweise ist die
Skalierung von Blockchains. ZKPs ermöglichen das „Komprimieren“ von Berechnungen für Blockchain-Transaktionen, ohne die Sicherheit zu beeinträchtigen.
In diesem Artikel beschreiben wir, wie Zero-Knowledge (insbesondere Bulletproofs ) angewendet werden kann, um mithilfe der Exonum-Plattform von Bitfury einen datenschutzorientierten Dienst aufzubauen.
Situationsanalyse
Mit dem „Walled Garden“ -Ansatz, bei dem die Daten ausgeblendet werden, weil der Zugriff auf sie mithilfe von Firewalls, rollenbasierter Zugriffskontrolle,
Wassergräben und anderen Perimeter-Sicherheitsmaßnahmen eingeschränkt wird, ist es möglich, ein
gewisses Maß an Datenschutz in Blockchain-Apps zu erreichen . Sensible Daten in der Blockchain können verschlüsselt (möglicherweise mit einem Verschlüsselungsschema mit öffentlichem Schlüssel, wobei die relevanten öffentlichen Schlüssel von derselben Blockchain verwaltet werden) und / oder außerhalb der Blockchain gespeichert werden (in diesem Fall speichert die Blockchain nur Hash-Fingerabdrücke von die Daten). Dieser Ansatz wird in vielen genehmigten Frameworks für verteilte Hauptbücher verwendet.
Die Nachteile des Ansatzes des „ummauerten Gartens“ werden jedoch immer deutlicher. Um es ganz klar auszudrücken, der Ansatz steht im Widerspruch zu einem der Hauptverkaufsargumente der Blockchain - der Überprüfbarkeit. Wenn die Daten in der Blockchain nicht durch Konsultieren der intelligenten Vertragslogik überprüft werden können, wird die Blockchain zu einem verherrlichten
verknüpften Zeitstempeldienst . Die Tatsache, dass sich einige Daten in der Blockchain befinden, bedeutet nicht mehr, dass diese Daten gemäß den Regeln für intelligente Verträge gültig sind. Der zweite große Nachteil des Ansatzes mit ummauerten Gärten besteht darin, dass er nicht skaliert. Richard Brown, CTO von R3, hat beispielsweise das Datenschutzmodell seiner Lösung treffend
mit Slack-Kanälen
verglichen. Es ist schwierig, Teilnehmer sicher zum Garten hinzuzufügen oder daraus zu entfernen, umso mehr, wenn keine vorherigen Erwartungen hinsichtlich der Anzahl und Identität dieser Kanäle bestehen Teilnehmer.
Hier kann Nullwissen wertvoll sein. Von Natur aus beweisen wissensfreie Beweise und Argumente¹ überzeugend eine Aussage über private Daten, ohne etwas über die Daten preiszugeben, außer die Aussage, die bewiesen wird. Es ist einfach, wissensfreie Beweise
universell überprüfbar zu machen, ohne dabei die Privatsphäre zu beeinträchtigen! ² Diese Funktion ist genau das, was erforderlich ist, um ein System zu erstellen, das sowohl die Privatsphäre schützt als auch gleichzeitig überprüfbar ist.
Unsere Forschung
Um die Verwendung von Proofs ohne Wissen zu demonstrieren, erstellen wir einen Kryptowährungsdienst mit ähnlichen Funktionen wie die Lernprogramme in der
Exonum-Dokumentation . Der Dienst ermöglicht die Registrierung von Benutzern und Geldbörsen (Bereitstellung eines anfänglichen Token-Guthabens als Belohnung) und die Übertragung von Token zwischen registrierten Parteien. Alle Transaktionen werden mithilfe eines Kryptosystems mit digitaler Signatur, Ed25519, authentifiziert, das in Exonum-Dienste integriert ist. Wir verbergen nicht die Identität von Transaktionspartnern (dh deren öffentlichen Schlüsseln), sondern die Anzahl der zu transaktionierenden Token und den Kontostand jedes Kontos im System. Wir diskutieren am Ende des Artikels auch, wie wir den Service verbessern können, um die Transaktionsentitäten auszublenden.
Der Service ist vollständig Open-Source und kann hier abgerufen
werden .
Kryptographie Hintergrund
Um zu verstehen, wie der Dienst funktioniert, müssen wir uns zunächst mit dem kryptografischen Grundelement von Bulletproofs vertraut machen - einem Konzept namens
Pedersen Commitments . Ein kryptografisches Commitment-Schema ähnelt einer Hash-Funktion: Jemand gibt geheime Daten ein (die Öffnung) und erhält die Ausgabe, die nicht erkennbar verschlüsselt ist (Commitment). Man kann dann die Öffnung aufdecken, um zu beweisen, dass der festgeschriebene Wert ihm entspricht.
Der Unterschied zu Hash-Funktionen besteht darin, dass nicht nur
verbindlich ist (niemand kann zwei verschiedene Öffnungen entwerfen, die dieselbe Verpflichtung erzeugen), sondern auch ein Verpflichtungsschema
verborgen bleibt (es ist unmöglich, das Schema umzukehren und eine Öffnung zu erzeugen, wenn eine Verpflichtung vorliegt). Eine Hash-Funktion wird ausgeblendet, wenn ihre Eingabe gleichmäßig über den gesamten Eingaberaum verteilt ist. Diese Annahme gilt jedoch am häufigsten nicht für Commitments (tatsächlich muss es möglich sein, einen Wert aus einer sehr kleinen Menge wie Boolean festzulegen). Als solches enthält die Öffnung neben der Nutzlast den
Verblindungsfaktor, der es (zumindest statistisch) unwahrscheinlich macht, die Nutzlast angesichts der Verpflichtung zu erraten.
Das Pedersen-Verpflichtungsschema verwendet eine
Gruppe erster Ordnung , in der das
Problem des
diskreten Logarithmus (DLP) zusammen mit zwei Generatoren,
G und
H , als schwierig angesehen wird.
G und
H müssen so gewählt werden, dass die diskrete logarithmische Beziehung zwischen ihnen unbekannt ist; Mit anderen Worten, niemand kennt
k so, dass
H = kG .³ Die Öffnung ist ein Paar
(x, r) , wobei
x der festgeschriebene Wert und
r der Verblindungsfaktor ist; Beide sind Gruppenskalare (im Wesentlichen Ganzzahlen mit „Überlauf“, die endlichen Ganzzahltypen ähneln, die in den meisten Programmiersprachen verwendet werden). Die Verpflichtung wird berechnet als
Comm (x; r) = xG + rH . Es kann bewiesen werden, dass das Pedersen-Engagement rechnerisch bindend ist und sich perfekt versteckt, wenn DLP in der Gruppe schwierig ist. “
Die entscheidende Eigenschaft für Pedersen-Verpflichtungen ist, dass sie additiv sind: Die Summe (oder Differenz) von 2 Verpflichtungen ist eine Verpflichtung zur Summe (oder Differenz) der zugesagten Werte. In der Tat,
C1 = x1 G + r1 H; C2 = x2 G + r2 H => C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
Wir geben hier keine Details dazu an, wie Kugelsicherungen erstellt und überprüft werden. Weitere Informationen finden Sie in den folgenden Ressourcen - [
1 ] und [
2 ]. Es genügt zu beachten, dass angenommen wird, dass die obere Bereichsgrenze
M die Form
2 ^ (2 ^ n) hat , was zu der effizientesten Beweiskonstruktion führt.
Aufbau eines Dienstes
Mit unserem Wissen können wir Kontoguthaben und Überweisungsbeträge mithilfe von Pedersen-Verpflichtungen sicher verbergen. Mithilfe von Entfernungsnachweisen können wir nachweisen / überprüfen, ob eine Übertragung korrekt ist:
- Der überwiesene Betrag ist positiv
- Der Absender hat genügend Guthaben auf seinem Konto.
Für den ersten Beweis nehmen wir die Verpflichtung zum Überweisungsbetrag
C_a (dieser ist direkt in der Überweisungstransaktion vorhanden) und überprüfen, ob der in
C_a-Comm (1; 0) festgeschriebene Wert im Bereich
[0, M] liegt. . Dies ist in der Tat gleichbedeutend mit dem Nachweis, dass
C_a einem Wert im Bereich
[1, M] entspricht . Der Absender kann diesen Nachweis erbringen, da er den überwiesenen Betrag
a kennt.
Für den zweiten Beweis müssen wir die Verpflichtung für den aktuellen Saldo des Absenders,
C_s , übernehmen und überprüfen, ob der in
C_s-C_a festgeschriebene Wert im Bereich
[0, M ] liegt. Wieder kann der Absender diesen Beweis vorlegen, da er die Öffnung sowohl für
C_s als auch für
C_a kennt .
Um die Übertragung auf den Blockchain-Status anzuwenden, subtrahieren wir die
Betragsverpflichtung C_a von der
Kontostandverpflichtung des Absenders (wie wir überprüft haben, kann dies nicht zu einem negativen Kontostand oder zur Erhöhung des Kontostands des Absenders führen) und addieren dann
C_a zum Empfänger Balance Engagement.
Wichtige Details
Es ist wichtig zu beachten, dass es einige Bedingungen gibt, die den implementierten Dienst komplexer machen können.
Der Empfänger einer Überweisung muss von irgendwo aus die Öffnung zu
C_a herausfinden ; Andernfalls kennt er die Öffnung zu seinem Gleichgewicht nicht mehr und kann mit seiner Brieftasche nichts mehr tun. Die Öffnung ist im Klartext der Übertragungstransaktion nicht vorhanden (das ist der gesamte Punkt). Wir
könnten annehmen, dass der Empfänger die Öffnung zuverlässig über einen Off-Chain-Kanal erhält (z. B. vom Absender per Telegramm gesendet), aber das ist kein veranschaulichendes Szenario. Stattdessen verschlüsseln wir die Öffnung mit einer Zwei-Parteien-Verschlüsselung mit öffentlichem Schlüssel basierend auf dem Diffie-Hellman-Schlüsselaustausch (libsodium nennt diese Art von Verschlüsselungsbox). Für den zusätzlichen Vorteil können Curve25519-Schlüssel, die für die
Box- Routine erforderlich sind, aus Ed25519-Schlüsseln konvertiert werden, sodass wir weiterhin ein einzelnes Schlüsselpaar für jeden Benutzer verwenden können, anstatt separate Verschlüsselungsschlüssel einzuführen

Sobald wir die Verschlüsselung eingeführt haben, können wir die Übertragung nicht mehr atomar anwenden. In der Tat kann der Absender böswillig oder unbeabsichtigt Müll anstelle der öffnenden Verschlüsselung bereitstellen, und die Blockchain-Logik kann nicht erkennen, dass dies der Fall ist. Daher bitten wir den Empfänger, die Übertragung explizit über eine separate Transaktion zu akzeptieren.
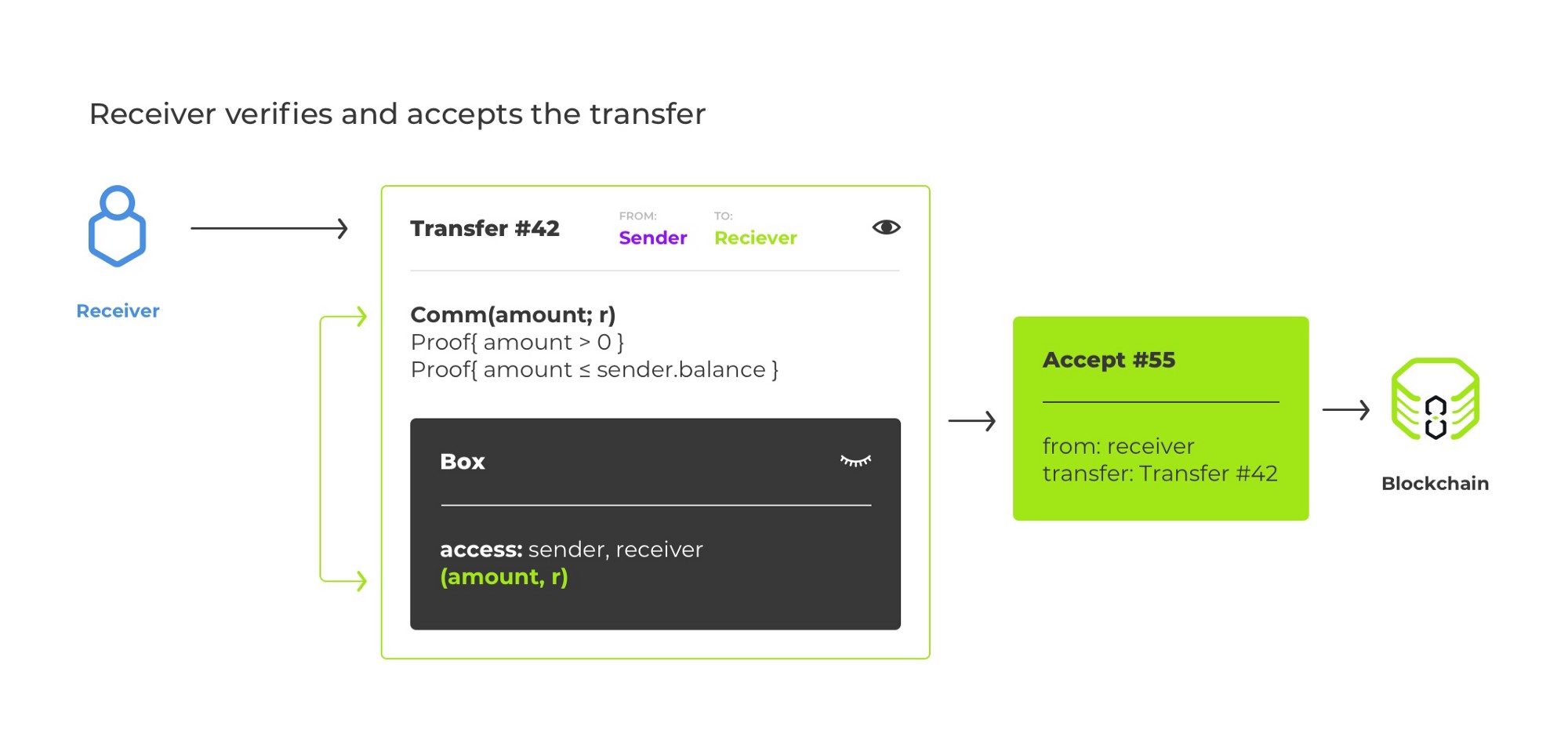
Bevor eine Überweisung akzeptiert wird, ändert sich die Kontostandverpflichtung des Absenders (andernfalls würden wir doppelte Ausgaben zulassen!), Nicht jedoch die des Empfängers.

Sobald die Annahme-Transaktion vom Blockchain-Netzwerk bestätigt wurde, wird der Kontostand des Empfängers aktualisiert und die Übertragung ist abgeschlossen.

Um Deadlocks zu vermeiden, gibt eine Übertragung eine Zeitsperrverzögerung (in relativer Blockchain-Höhe,
a la Bitcoin's
CSV ) an, damit der Empfänger die Akzeptanz signalisiert. Wenn die Zeitsperre abgelaufen ist, wird die Überweisung automatisch an den Absender zurückerstattet (Exonum ermöglicht dies über den Hook
Service :: beforeCommit () ).
Ein weiteres Problem ist komplizierter. Um den Nachweis eines ausreichenden Guthabens zu erbringen, muss der Absender sein aktuelles Guthaben kennen, was möglicherweise nicht immer der Fall ist. Eine streunende Annahme-Transaktion oder Rückerstattung kann das Guthaben des Absenders unabsichtlich erhöhen. In diesem Fall schlägt die Überprüfung fehl und der Absender ist einigermaßen frustriert.
Um dieses Problem zu lösen, erlauben wir Überweisungen, auf den aktuellen Status des Absenders zu verweisen (genauer gesagt, die Anzahl der Ereignisse, die den Kontostand ändern - Überweisungen und Rückerstattungen). Bei der Überprüfung des Nachweises eines ausreichenden Guthabens verwenden wir den angegebenen Status, um die Saldoverpflichtung des Absenders zu erhalten. Außerdem überprüfen wir, ob seit dem referenzierten Status keine ausgehenden Übertragungen mehr aufgetreten sind. Wenn dies der Fall ist, können wir sicher sein, dass wir einen nicht negativen Wert erhalten, wenn wir den Überweisungsbetrag vom
aktuellen Saldo des Absenders abziehen. In der Tat können die Ereignisse im Kontoverlauf nach dem Referenzpunkt (eingehende Überweisungen und Rückerstattungen) den Kontostand nur erhöhen! ⁷
Mit vorhandenen Referenzpunkten ist der Absender immer noch etwas eingeschränkt. Beim Erstellen einer neuen Übertragung dürfen keine ausstehenden Übertragungen vorliegen. Diese Einschränkung ist jedoch weitaus weniger einschränkend als die Anforderung, den Kontostatus zum Zeitpunkt der Übertragung zu kennen. Grundsätzlich machen wir den Absender von dem abhängig, was
er zuvor getan hat, aber nicht von den Handlungen anderer.
Implementierung
Wir verwenden eine in reinem
Rust geschriebene Bulletproofs-Bibliothek, die vor kurzem das
Pre-Release-Stadium erreicht hat . Da die Exonum-Plattform in Rust geschrieben ist, lässt sie sich nahtlos in die Bibliothek integrieren. Als Bonus basiert die von uns verwendete Bibliothek im Gegensatz zu der im Original-Whitepaper beschriebenen Version von Bulletproofs (die in
C entwickelt wird und die elliptische Kurve secp256k1 von Bitcoin verwendet) auf Curve25519, die bereits in Exonum als Hauptkomponente von verwendet wird Kryptosystem für digitale Signaturen Ed25519.
Die Implementierung des Dienstes basierend auf der obigen Beschreibung ist recht einfach. Der schwierigste Teil bestand darin, Merkle-Beweise zu erstellen, die die an den Benutzer zurückgegebenen Informationen authentifizieren, damit er den Exonum-Knoten, mit denen er kommuniziert, nicht blind vertrauen muss. Die Verbesserung der Erfahrung von Serviceentwicklern in dieser Hinsicht ist eines der Hauptziele der
Exonum 1.0-Version .
Nächste Schritte
Der von uns erstellte Dienst verbirgt nicht die Identität des Absenders und des Empfängers von Übertragungen, was eine wesentliche Einschränkung für reale Anwendungen darstellt. Glücklicherweise gibt es Möglichkeiten, dieses Problem zu lösen.
Die in
zCash verwendete generische Technik (die jedoch hauptsächlich auf andere Anwendungsfälle wie
Ethereum anwendbar ist) basiert auf der Erstellung eines
Merkle-Baums des Systemstatus. Beispielsweise erstellt zCash den Notizverpflichtungsbaum, der in etwa den jemals in Bitcoin erstellten Transaktionsausgaben entspricht. Zero-Knowledge-Proofs umfassen dann Authentifizierungspfade (auch Merkle-Zweige genannt) in diesem Baum und enthüllen etwas über ein Element des Baums, ohne zu enthüllen, auf welches Element verwiesen wird. Der Nachteil dieses Ansatzes ist, dass es schwierig ist, kryptografische Hash-Funktionen, die zum Erstellen von Merkle-Bäumen verwendet werden, in den Bereich ohne Wissen zu übertragen. Die resultierenden Proofs werden rechenintensiv - die Erstellung eines einzelnen Proofs kann Sekunden oder sogar Minuten dauern. Die Suche nach „ZKP-freundlicheren“ kryptografischen Hash-Funktionen ist das Gebiet der aktiven Forschung.
Wenn wir zusätzliche Einschränkungen zulassen, gibt es möglicherweise eine einfachere Lösung. Ein kürzlich veröffentlichtes Papier von
Narula et al . beschreibt ein System mit einer begrenzten, a priori bekannten Anzahl von Teilnehmern, die untereinander Transaktionen durchführen können, ohne Teilnehmer oder übertragene Beträge für eine Transaktion preiszugeben. (Denken Sie an ein datenschutzorientiertes Blockchain-Netzwerk für Überweisungen zwischen Banken.)
Prosaischer ausgedrückt gibt es wahrscheinlich viele technische Verbesserungen, die der entwickelte Dienst genießen kann: mehr Testabdeckung, Trennung von Signatur- und Verschlüsselungsschlüsseln, Benchmarking usw. Eine wesentliche Verbesserung des Service UX wäre die deterministische Reihenfolge von Transaktionen, die von demselben Benutzer stammen und die wir nicht lange nach der Veröffentlichung von Exonum 1.0 lösen möchten.
Fazit
Wir haben beschrieben, wie ein kontobasiertes Kryptotoken mit starker Privatsphäre erstellt wird, das durch wissensfreie Beweise (insbesondere kugelsichere Beweise) ermöglicht wird. Die Token-Logik wurde als Exonum-Dienst implementiert. Obwohl der Dienst derzeit nur ein Proof of Concept ist, zeigt er, wie die Exonum-Plattform verwendet werden kann, um auf komplexen kryptografischen Grundelementen mit sehr geringem Overhead aufzubauen, der durch die Ausführungsumgebung verursacht wird.
- Es gibt eine komplizierte Unterscheidung zwischen Beweisen und Argumenten, auf die wir hier nicht eingehen werden. Der Einfachheit halber werden wir in diesem Artikel alle Konstruktionen ohne Wissen als Beweise ohne Wissen bezeichnen, auch wenn dies vom theoretischen Standpunkt aus nicht immer korrekt ist.
- Dies kann durch eine sehr allgemeine Technik erreicht werden, die als Fiat-Shamir-Transformation bekannt ist und ein interaktives Beweisprotokoll in ein nicht interaktives, universell überprüfbares Protokoll umwandelt. Wenn wir die wissenschaftliche Strenge erneut opfern, werden wir nicht explizit klarstellen, dass von uns verwendete wissensfreie Beweise nicht interaktiv sind.
- Generatoren werden normalerweise mit der Methode „Nichts im Ärmel“ ausgewählt. Zum Beispiel kann G ein Teil der Gruppenspezifikation für seine Verwendung in der Kryptographie mit öffentlichem Schlüssel sein, und H wird von G über eine Hash-Funktion abgeleitet: H ~ Hash (G) .
- Letzteres bedeutet, dass selbst ein Gegner mit unendlicher Rechenleistung nicht ableiten kann, wozu sich die Verpflichtung verpflichtet; Wenn DLP in der Gruppe nicht funktioniert, kann jede Verpflichtung für einen beliebigen Wert geöffnet werden.
- Dies ist teilweise eine Proof-of-Concept-Entscheidung. Im Allgemeinen ist die Wiederverwendung von Schlüsseln für verschiedene Zwecke eine schlechte Idee.
- Es ist theoretisch möglich, einen wissensfreien Beweis dafür zu liefern, dass der verschlüsselte Wert dem festgeschriebenen Guthaben entspricht. Dies würde jedoch die Systemkomplexität in unzulässiger Weise erhöhen.
- Es ist zu erwähnen, dass einige Übertragungen, die gegen die Regel „Keine ausgehenden Übertragungen seit dem Status, auf den verwiesen wird“ verstoßen, immer noch korrekt sein können. Wir haben einfach keine Möglichkeit, dies zu überprüfen.