Wenn Sie meinen ersten Artikel zu diesem Thema nicht gelesen haben, empfehle ich Ihnen, damit zu beginnen.
Da ich eine gewisse, wenn auch sehr indirekte Haltung gegenüber Finanzmathematikern erwähnte, möchte ich das Thema auf der Grundlage seiner Entwicklung in der Risikoanalyse bis zur Absurdität entwickeln. Bei der Berechnung des Preises einer Option wird häufig die Empfindlichkeit dieses Preises gegenüber einer Reihe von Parametern berücksichtigt. Zum Beispiel, wie sich der Optionspreis ändert, wenn sich der Preis der Aktie, für die die Option ausgegeben wird, ändert oder wenn sich die Volatilität des Aktienkurses oder der Kurs der Zentralbank ändert usw.
Es könnte uns interessieren, wie sich die Wahrscheinlichkeit, ein Spiel zu gewinnen, ändert, wenn sich die Wahrscheinlichkeit, einen Punkt zu gewinnen, ändert. Tatsächlich wollen wir die Ableitung von der ersten zur zweiten berechnen. Der einfachste Ansatz besteht darin, ihn anhand des Diagramms mit dem Auge zu bewerten. Es ist ersichtlich, dass das Maximum in einer Situation von 50:50 erreicht wird. Wenn sich die Gewinnchancen eines Punktes von 0,45 auf 0,55 ändern, steigt die Wahrscheinlichkeit, Badminton zu gewinnen, von 0,26 auf 0,74, dh um 0,48. Eine grobe Schätzung ergibt eine Ableitung im Bereich von 5. Das heißt, wenn Sie bei gleichen Chancen auf 0,51 (das sind 51%) heranwachsen, steigt die Wahrscheinlichkeit, das Spiel zu gewinnen, um 0,05 (oder 5%). Ebenso können Sie die Ableitung an jedem anderen Punkt im Diagramm berechnen.
Im Finanzbereich wird normalerweise der „Bump and Run“ -Ansatz verwendet, dh sie ändern den Parameter um einen kleinen Betrag und berechnen den neuen Optionspreis und das neue Derivat. Nachdem ich auf ähnliche Weise gehandelt habe, zitiere ich die genauen Daten in der Grafik (ich habe die Änderung in Prozent angenommen, etwas unhöflich, aber in dieser Situation akzeptabel). Für mehr Klarheit fügte er Spiele mit bis zu 5 und 31 Punkten hinzu. Übrigens kann das Schießen im Biathlon als Party bis zu 5 Personen betrachtet werden. Dies ist keine absolute Analogie, da die Gesamtzahl der Schüsse festgelegt ist. Die Lösungsmethoden sind jedoch fast gleich.
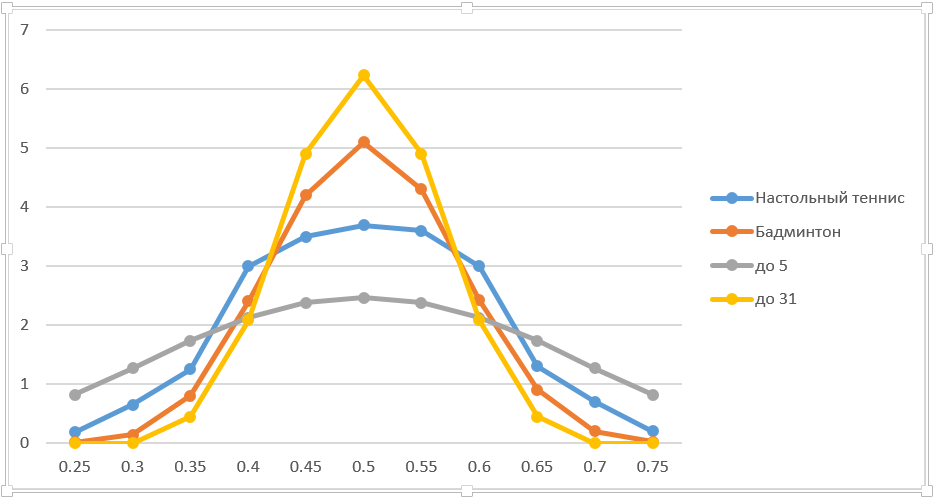
Je länger die Charge ist, desto höher ist natürlich die Ableitung bei 50:50. Wenn die Gruppenlänge gegen unendlich tendiert, ist der Sieg eines Spielers mit nur einem minimalen Vorteil praktisch garantiert. Die Breite der Kurve nimmt entsprechend ab. Im Allgemeinen liegen die Schlussfolgerungen auf der Hand.
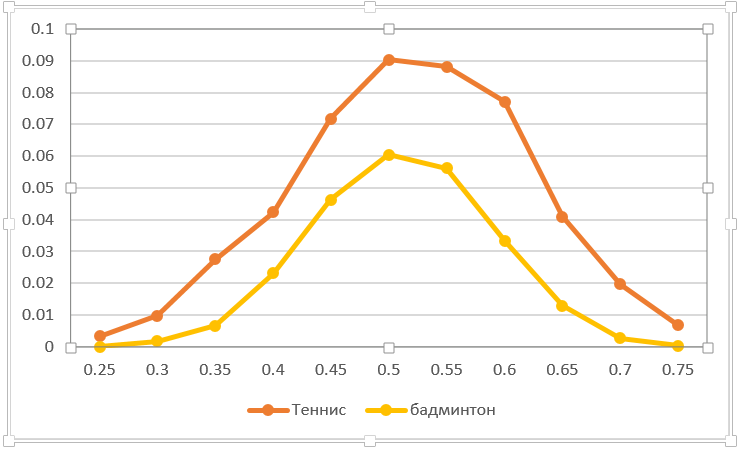
Sie können die Empfindlichkeit für die versehentliche Entladung eines Punktes berechnen. Zum Beispiel ins Netz einspeisen. Wie sehr beeinflusst ein Ausrutscher das Ergebnis des Spiels? In der Tat ist dies eine Verringerung der Gewinnpunktzahl für den Gegner um einen Punkt. Die folgende Grafik spiegelt diese Situation wider. Natürlich ist es beim Tischtennis wichtiger, einen Punkt zu verlieren als beim Badminton. Bei gleichen Kräften sinkt die Wahrscheinlichkeit des Spielergebnisses so weit wie möglich - von 0,5 auf 0,41. Achten Sie auf die Asymmetrie der Kurven (im Gegensatz zu den meisten anderen). Das ist kein Zufall. Tatsache ist, dass sich das Gleichgewicht von 50:50 zu einer höheren Wahrscheinlichkeit verschiebt, einen Punkt zu gewinnen, da ein verlorener Punkt die Chancen eines Spielers verschlechtert.
Lassen Sie uns eine weitere interessante Erfahrung machen. Stellen Sie sich vor, einer der Spieler kann sich konzentrieren und 3 Punkte über dem Durchschnitt spielen (p1 + Delta). Angenommen, danach kehrt die Ausrichtung zum Original zurück (auf den erwarteten Durchschnitt ohne Berücksichtigung des "Kraftanstiegs"). Es ist klar, dass die Gewinnwahrscheinlichkeit steigen wird. Die Frage ist, spielt es eine Rolle, wann man sich konzentrieren muss - zu Beginn oder am Ende des Spiels? Ich schlage vor, eine Annahme zu machen, bevor ich weiter lese.
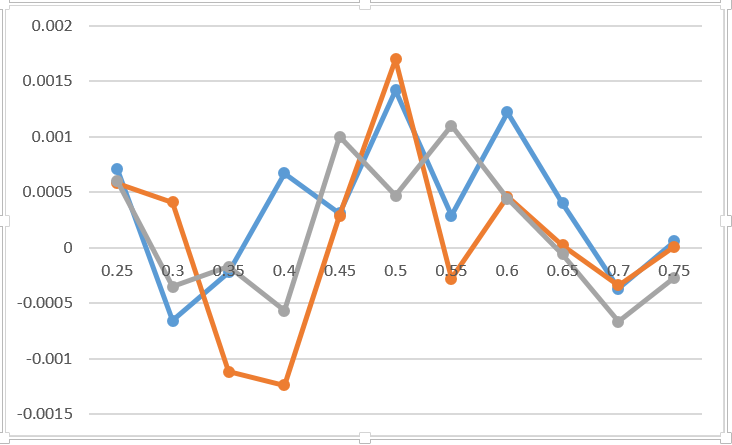
Wie das Experiment zeigt, gibt es absolut keinen Unterschied, wann genau konzentriert werden muss (Faktoren des moralischen Plans werden nicht berücksichtigt). Die Grafik zeigt den Unterschied zwischen der Wahrscheinlichkeit, das Spiel bei Konzentration an 3 verschiedenen Stellen des Spiels zu gewinnen, und der Konzentration auf die ersten 3 Punkte. Ich denke, diese Grafik spiegelt den Fehler von Monte Carlo wider und nichts weiter. Ich habe 0,2 zum Ergebnis der Punktziehung für den ersten Spieler für drei Ziehungen hinzugefügt. Ich gebe in der Tabelle nicht einmal an, welche Linie welcher Option entspricht. Es ändert definitiv nichts. Der einzige wertvolle Ratschlag zu diesem Thema ist, sich fertig zu machen, bevor es zu spät ist.
Lassen Sie uns nun überlegen, was passieren wird, wenn einer der Spieler Stabilität hat. Nerven sind Nerven, ein verantwortungsbewusstes Spiel passiert. Angenommen, er erhält im Durchschnitt den gleichen Prozentsatz an Punkten, aber wenn er einen bestimmten Punkt zieht, schwebt dieser Prozentsatz. Zum Beispiel wird die Hälfte der Punkte mit der Wahrscheinlichkeit p1 + Delta und die andere Hälfte mit p1-Delta gespielt. In diesem Fall bleibt der Durchschnitt p1 das Original, der Verlust von + Delta oder –Delta tritt zufällig mit einer Wahrscheinlichkeit von 0,5 auf. Wird es irgendwie das Ergebnis des Spiels beeinflussen? Wie meine Experimente mit Hilfe von Monte Carlo gezeigt haben, ist der Unterschied praktisch nicht nachvollziehbar. Wenn wir einen bestimmten Betrag addieren oder subtrahieren, bleiben wir bei der gleichen durchschnittlichen Wahrscheinlichkeit, einen Punkt zu gewinnen. Der Vorschlag legt nahe, dass die Verteilungskurve nicht das Ergebnis des Spiels beeinflusst, sondern nur den Durchschnitt, aber ich werde es nicht auf mich nehmen. Hier muss man nachdenken.
Ich möchte auch eine Differentialgleichung wie Black Scholes in Finance ableiten, um die Assoziation zu vervollständigen. Identifizieren Sie signifikante Ableitungen, setzen Sie die zufällige Komponente auf Null ... Wir müssen uns auch mit Diskretion befassen. Vielleicht überlasse ich das echten Finanzmathematikern.