🗒️ 🤳🏾 🤘🏿 Julia und Optimierung 👨🏼 📺 🙎🏿

Es ist Zeit, Pakete in Betracht zu ziehen, die Methoden zur Lösung von Optimierungsproblemen bieten. Viele Probleme können darauf reduziert werden, das Minimum einer Funktion zu finden. Sie sollten also ein paar oder zwei Löser im Arsenal haben, und noch mehr ein ganzes Paket.

Eintrag

Die Julia-Sprache wird immer beliebter . Unter https://juliacomputing.com können Sie sehen, warum Astronomen, Robotiker und Finanziers diese Sprache wählen, und unter https://academy.juliabox.com können Sie kostenlose Kurse starten, um die Sprache zu lernen und sie für jede Art von maschinellem Lernen zu verwenden. Für diejenigen, die ernsthaft beschlossen haben, mit dem Lernen zu beginnen, empfehle ich Ihnen, das Video anzusehen, Artikel zu lesen und auf Jupiter-Laptops unter https://julialang.org/learning/ zu klicken oder zumindest den Hub von unten nach oben zu durchlaufen : Es wird Installation, Funktionen und Anwendung für Unternehmen geben dringend. Kommen wir nun zu den Bibliotheken.

Blackboxoxptim

BlackBoxOptim - globales Optimierungspaket für Julia ( http://julialang.org/ ). Es unterstützt sowohl Mehrzweck- als auch Einzweck-Optimierungsprobleme und konzentriert sich auf (meta) heuristische / stochastische Algorithmen (DE, NES usw.), bei denen die optimierte Funktion im Gegensatz zu herkömmlichen deterministischen Algorithmen NICHT differenzierbar sein muss. die oft auf Gradienten / Differenzierbarkeit basieren. Es unterstützt auch paralleles Rechnen, um die Optimierung von Funktionen zu beschleunigen, die langsam ausgewertet werden.

Laden Sie die Bibliothek herunter und verbinden Sie sie

]add BlackBoxOptim using BlackBoxOptim

Stellen Sie die Rosenbrock-Funktion ein:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Wir suchen nach einem Minimum für das Intervall (-5; 5) für jede Koordinate für ein zweidimensionales Problem:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

Was die Antwort folgen wird:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

und viele unlesbare Daten, aber ein Minimum wurde gefunden. Da stochastisch verwendet wird, sind Funktionsaufrufe etwas umfangreich. Für mehrdimensionale Aufgaben ist es daher besser, die Auswahl der Methoden zu verwenden

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Konvex

Convex ist Julias Paket für disziplinierte konvexe Programmierung (disziplinäre konvexe Programmierung?). Convex.jl kann lineare Programme, gemischte ganzzahlige lineare Programme und DCP-kompatible konvexe Programme mit verschiedenen Lösern, einschließlich Mosek, Gurobi, ECOS, SCS und GLPK, über die MathProgBase-Schnittstelle lösen. Es unterstützt auch die Optimierung mit komplexen Variablen und Koeffizienten.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

Es gibt viele Beispiele auf der Website: Tomographie (der Prozess der Wiederherstellung der Dichteverteilung durch gegebene Integrale über die Verteilungsbereiche. Sie können beispielsweise mit Tomographie in Schwarzweißbildern arbeiten), Maximierung der Entropie, logistische Regression, lineare Programmierung usw.

Zum Beispiel müssen Sie die folgenden Bedingungen erfüllen:

\ begin {array} {ll} \ mbox {befriedige} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}

$\ begin {array} {ll} \ mbox {befriedige} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

Wird eine Antwort geben

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

Springe

JuMP ist eine domänenspezifische mathematische Optimierungssprache, die in Julia integriert ist. Derzeit unterstützt er eine Reihe offener und kommerzieller Löser (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).

JuMP macht es einfach, Optimierungsprobleme ohne Expertenwissen zu identifizieren und zu lösen, ermöglicht es Experten jedoch gleichzeitig, fortschrittliche algorithmische Methoden zu implementieren, z. B. die Verwendung effektiver „Hot“ -Starts in der linearen Programmierung oder die Verwendung von Rückrufen zur Interaktion mit Verzweigungs- und Grenzlösern. JuMP ist auch schnell - Benchmarking hat gezeigt, dass es Berechnungen mit ähnlichen Geschwindigkeiten wie spezielle kommerzielle Tools wie AMPL verarbeiten kann, während die Ausdruckskraft einer universellen Programmiersprache auf hohem Niveau erhalten bleibt. JuMP kann problemlos in komplexe Workflows wie Simulationen und Webserver integriert werden.

Mit diesem Tool können Sie Aufgaben wie:

LP = lineare Programmierung
QP = Quadratische Programmierung
SOCP = konische Programmierung zweiter Ordnung (einschließlich Probleme mit konvexen quadratischen Bedingungen und / oder Zweck)
MILP = Mixed Integer Linear Programming
NLP = Nichtlineare Programmierung
MINLP = gemischte ganzzahlige nichtlineare Programmierung
SDP = semi-definierte Programmierung
MISDP = Semidefinite-Programmierung mit gemischten Ganzzahlen

Die Analyse seiner Funktionen wird für mehrere Artikel ausreichen. Gehen wir daher zunächst zu folgenden Punkten über:

Optim

Optim Es gibt viele Löser, die sowohl aus kostenlosen als auch aus kommerziellen Quellen verfügbar sind, und viele sind bereits für die Verwendung in Julia verpackt. Nur wenige von ihnen sind in dieser Sprache geschrieben. In Bezug auf die Leistung ist dies selten ein Problem, da sie häufig entweder in Fortran oder C geschrieben sind. Löser, die direkt in Julia geschrieben sind, haben jedoch einige Vorteile.

Beim Schreiben von Julia-Software (Paketen), für die etwas optimiert werden muss, kann der Programmierer entweder sein eigenes Optimierungsverfahren schreiben oder einen der vielen verfügbaren Löser verwenden. Zum Beispiel könnte es etwas aus dem NLOpt-Set sein. Dies bedeutet, dass Sie eine Abhängigkeit hinzufügen, die nicht in Julia geschrieben ist, und dass Sie mehr Annahmen über die Umgebung treffen müssen, in der sich der Benutzer befindet. Hat der Benutzer die richtigen Compiler? Kann ich GPL-Code in einem Projekt verwenden?

Es ist auch richtig, dass die Verwendung eines in C oder Fortran geschriebenen Lösers es unmöglich macht, einen der Hauptvorteile von Julia zu nutzen: Mehrfachversand. Da Optim vollständig in Julia geschrieben ist, können wir derzeit ein Versandsystem verwenden, um die Verwendung benutzerdefinierter Voreinstellungen zu vereinfachen. Eine geplante Funktion in dieser Richtung besteht darin, eine benutzergesteuerte Auswahl von Lösern für die verschiedenen Stufen des Algorithmus zu ermöglichen, die ausschließlich auf dem Versand und nicht auf den von Optim-Entwicklern ausgewählten vordefinierten Funktionen basiert.

Ein Paket auf Julia bedeutet auch, dass Optim über Pakete in JuliaDiff Zugriff auf automatische Differenzierungsfunktionen hat .

Anleitung

Weiter:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

Wir erhalten eine Antwort mit einem praktischen Bericht:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

Und vergleiche mit meinem Nelder Mead!

Spoiler

Meins wird langsamer sein :(

Versteckt

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

Im Verlauf der Überprüfung stellte sich auch heraus, dass meine Implementierung nicht funktioniert, wenn Sie die anfängliche Näherung (0, 0) verwenden. Als Stoppkriterium können Sie das Volumen des Simplex verwenden , aber ich verwende die Norm einer Matrix, die aus Eckpunkten besteht. Hier können Sie über die geometrische Interpretation der Norm lesen . In beiden Fällen wird eine Matrix von Nullen erhalten - ein Sonderfall einer entarteten Matrix, daher führt das Verfahren keine Schritte aus. Sie können die Erstellung eines Start-Simplex konfigurieren, indem Sie beispielsweise den Abstand seiner Scheitelpunkte von der anfänglichen Näherung festlegen (und nicht wie bei mir - die halbe Länge des Vektors, fu, was für eine Schande ...). Dann ist die Methodeneinstellung flexibler oder stellen Sie sicher, dass nicht alle Scheitelpunkte vorhanden sind saß an einem Punkt:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

Nun ja, mein Simplex Goraaazdo ist langsamer:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

Jetzt mehr Grund, zum Studienpaket zurückzukehren

Sie können die verwendete Methode auswählen:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

und erhalten Sie detaillierte Dokumentation und Verweise darauf

 ?LBFGS()

Sie können jakobianische und hessische Funktionen einstellen

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

Wie Sie sehen können, hat er automatisch die Newton-Methode ausgearbeitet. So können Sie den Suchbereich einstellen und den Gradientenabstieg verwenden:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

Angenommen, Sie wollten die Gleichung lösen, oder ich weiß nicht

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

und er hat dir die Brent-Methode ausgesucht.
Wenn Sie experimentelle Daten haben, müssen Sie die Modellkoeffizienten optimieren

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0, 2

$p_1 = 1, p_2 = 0,2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

Bonus Erstellen Sie Ihre Testfunktion

Die Idee stammt aus dem Artikel von Chabrow . Sie können jedes lokale Minimum selbst konfigurieren:

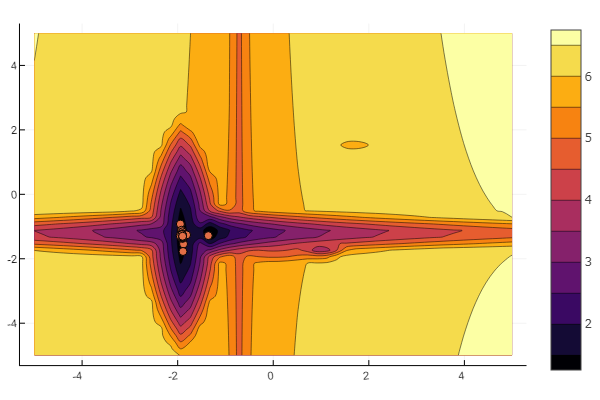
 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Und du kannst alles dem Willen des allmächtigen Zufalls überlassen

 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Aber wie Sie auf dem Startbild sehen können, ist ein Partikelschwarm mit einem solchen Relief nicht einschüchternd.

Dies sollte getan werden. Wie Sie sehen können, verfügt Julia über eine ziemlich leistungsfähige und moderne mathematische Umgebung, die komplexe numerische Studien ermöglicht, ohne sich auf Programmierabstraktionen auf niedriger Ebene zu beschränken. Und dies ist eine hervorragende Gelegenheit, diese Sprache weiter zu lernen.

Viel Glück an alle!