In diesem Artikel stelle ich eine neue quasi zufällige Sequenz mit geringer Divergenz vor, die eine signifikante Verbesserung gegenüber modernen Sequenzen wie Sable, Niederreiter usw. bietet.Figure 1. Vergleich verschiedener quasi-zufälliger Sequenzen mit geringer Divergenz. Beachten Sie, dass die von mir vorgeschlagenen R. -Sequenz erzeugt gleichmäßigere Punkte als alle anderen Methoden. Darüber hinaus erfordern alle anderen Methoden eine sorgfältige Auswahl der Grundparameter und führen bei falscher Auswahl zu einer Entartung (z. B. oben rechts).In diesem Artikel behandelte Themen- Sequenzen mit geringer Divergenz in einer Dimension
- Methoden mit geringer Divergenz in zwei Dimensionen
- Packabstand
- Multiklassen-Sets mit geringer Diskrepanz
- Quasi zufällige Sequenzen auf der Oberfläche einer Kugel
- Quasiperiodische Flugzeugkacheln
- Dithering-Masken in Computergrafiken
Vor einiger Zeit wurde dieser Beitrag auf der Hacker News Homepage veröffentlicht. Dort können Sie seine
Diskussion lesen.
Einleitung: zufällig versus quasi zufällig
In Abbildung 1 können Sie feststellen, dass bei einer einfachen einheitlichen Zufallsstichprobe eines Punktes innerhalb eines Einheitsquadrats eine Ansammlung von Punkten beobachtet wird und auch Bereiche ohne Punkte („weißes Rauschen“) entstehen. Eine quasi-zufällige
Sequenz mit geringer Divergenz ist eine Methode zur deterministischen Konstruktion (unendlicher) aufeinanderfolgender Punkte, die die Wahrscheinlichkeit einer Akkumulation (Divergenz) verringert und gleichzeitig eine gleichmäßige Abdeckung des gesamten Raums gewährleistet („blaues Rauschen“).
Quasi zufällige Sequenzen in einer Dimension
Die Methoden zur Erzeugung vollständig bestimmter Quasirandom-Sequenzen mit geringer Divergenz in einer Dimension sind sehr gut untersucht und allgemein gelöst. In diesem Beitrag werde ich hauptsächlich offene (unendliche) Sequenzen betrachten, zuerst in einer Dimension, und dann zu höheren Dimensionen übergehen. Der grundlegende Vorteil offener Sequenzen (d. H. Erweiterbar in
n ) liegt in der Tatsache, dass, wenn die Gesamtfehler basierend auf einer endlichen Anzahl von Elementen zu groß sind, die Sequenz erweitert werden kann, ohne alle zuvor berechneten Punkte zu verwerfen. Es gibt viele Möglichkeiten, offene Sequenzen zu erstellen. Sie können verschiedene Typen in Kategorien unterteilen, indem Sie ihre grundlegenden (Hyper-) Parameter erstellen:
- irrationale Fraktionen: Kronecker, Richtmayer, Ramshaw
- (gegenseitig) Primzahlen: Van der Corpute, Holton, Foret
- Irreduzible Polynome: Niederreiter
- Primitive Polynome: Sable
Der Kürze halber werde ich in diesem Beitrag hauptsächlich das neue
rekursive Additiv vergleichen
R. - eine Sequenz, die zur ersten Kategorie gehört, dh zu rekursiven Methoden, die auf irrationalen Zahlen basieren (oft als Kronecker-,
Weil- oder Richtmeier-Sequenzen bezeichnet), die Gitter vom Rang 1 sind, und eine Holton-Sequenz, die auf der kanonischen eindimensionalen Van-der-Corpute-Sequenz basiert. Die kanonische rekursive Folge von Kronecker ist definiert als:
R_1 (\ alpha): \; \; t_n = \ {s_0 + n \ alpha \}, \ quad n = 1,2,3, ...
wo
alpha - jede irrationale Zahl. Beachten Sie, dass der Eintrag
\ {x \} bezeichnet den Bruchteil
x . In Berechnungen wird diese Funktion häufig ausgedrückt als
R1( alpha):tn=s0+n alpha( textrmmod1); quadn=1,2,3,...
Bei
s0=0 erste Mitglieder der Sequenz
R( phi) gleich:
tn=0,618,0,236,0,854,0,472,0,090,0,708,0,327,0,944,0,562,0,180,798,416,0,034,0,652,0,271,0,888,...
Es ist wichtig zu beachten, dass die Bedeutung
s0 wirkt sich nicht auf die allgemeinen Eigenschaften der Sequenz aus und ist in fast allen Fällen gleich Null. Bei der Berechnung der Option
s neq0 bietet einen zusätzlichen Freiheitsgrad, der oft nützlich ist. Wenn
s neq0 dann wird die Sequenz oft als "verschobene Gittersequenz" bezeichnet. Trotz der Tatsache, dass standardmäßig
s=0 Ich glaube, dass es theoretische und praktische Überlegungen gibt, für die der Wert Standard sein sollte
s=1/2 . Wert
alpha Geben der kleinstmöglichen Diskrepanz, wenn
alpha=1/ phi wo
phi - Dies ist der goldene Schnitt. Also
phi equiv frac sqrt5+12 simeq1.61803398875...;
Es ist interessant festzustellen, dass es unendlich viele andere Werte gibt.
alpha , die es uns auch ermöglichen, die optimale Diskrepanz zu erhalten, und die alle durch die Mobius-Transformation miteinander verbunden sind
alpha′= fracp alpha+qr alpha+s quad textrmfüralleganzenZahlenp,q,r,s quad textrmsodass|ps−qr|=1
Nun vergleichen wir diese rekursive Methode mit den bekannten van der Korput-Sequenzen mit umgekehrter Reihenfolge der Entladungen [
van der Korput, 1935 ]. Van der Corpute-Sequenzen sind eigentlich eine Familie von Sequenzen, von denen jede durch einen eindeutigen Hyperparameter definiert ist
b . Die ersten Mitglieder der Sequenz mit b = 2 sind gleich:
t[2]n= frac12, frac14, frac34, frac18, frac58, frac38, frac78, frac116, frac916, frac516, frac1316, frac316, frac1116, frac716, frac1516,...
Im nächsten Abschnitt vergleichen wir die allgemeinen Eigenschaften und die Wirksamkeit jeder dieser Sequenzen. Betrachten Sie das Problem der Berechnung eines bestimmten Integrals
A= int10f(x) textrmdx
Wir können es approximieren als:
A simeqAn= frac1n sumni=1f(xi), quadxi in[0,1]
- Wenn \ {x_i \} sind gleich i/n Dies ist die Formel der Rechtecke .
- Wenn \ {x_i \} zufällig ausgewählt, dann ist dies die Monte-Carlo-Methode ; aber
- Wenn \ {x_i \} Sind Elemente einer Sequenz mit geringer Divergenz, so ist dies die Quasi-Monte-Carlo-Methode .
Die folgende Grafik zeigt typische Fehlerkurven.
sn=|A−An| um ein bestimmtes Integral zu approximieren, das mit dieser Funktion verbunden ist,
f(x)= textrmexp( frac−x22),x in[0,1] für: (i) quasi zufällige Punkte aus der additiven Rekursion, wobei
alpha=1/ phi (blau); (ii) quasi zufällige Punkte aus der Van-der-Corput-Sequenz (orange); (iii) zufällig ausgewählte Punkte (grün); (iv) Zobelsequenzen (rot).
Dies zeigt, dass für
n=106 Punktelösung mit Zufallsstichprobe führt zu einem Fehler
simeq10−4 Die Van-der-Corput-Sequenz führt zu einem Fehler
simeq10−6 , während
R( phi) - Die Reihenfolge führt zu einem Fehler
simeq10−7 das in
sim 10 mal besser als der Fehler von van der Corput und
sim 1000-mal besser als (einheitliche) Zufallsstichproben.
Figure 2. Vergleich der eindimensionalen numerischen Integration mit verschiedenen quasi-zufälligen Monte-Carlo-Methoden. Je niedriger der Wert, desto besser. Neu R2 - Die Sequenz (blau) und die Sable-Sequenz (rot) sind offensichtlich die besten.Folgendes ist hier erwähnenswert:
- dies entspricht dem Wissen, dass die Fehler für eine gleichmäßige Zufallsstichprobe asymptotisch auf abnehmen 1/ sqrtn und der Fehler für beide quasi zufälligen Sequenzen tendiert dazu 1/n .
- Ergebnisse für R1( phi) -Sequenzen (blau) und Sable-Sequenzen (rot) sind die besten.
- Die Grafik zeigt, dass die Van-der-Corpute-Sequenz gute, aber unglaublich konsistente Ergebnisse für Integrationsaufgaben liefert!
- Hier ist zu sehen, dass für alle Werte n Sequenz R1( phi) liefert bessere Ergebnisse als die Van-der-Corput-Sequenz.
Neue Sequenz R1 Dies ist eine Kronecker-Sequenz mit dem Goldenen Schnitt und eine der besten Optionen für eindimensionale quasirandomale Monte-Carlo-Integrationsmethoden (QMC).
Es ist auch erwähnenswert, dass obwohl
alpha= phi bietet theoretisch eine nachweislich optimale Option,
sqrt2 sehr nahe am Optimum und fast jeder andere irrationale Wert
alpha bietet überlegene Fehlerkurven für die eindimensionale Integration. Deshalb wird es sehr oft verwendet
alpha= sqrtp für jede Primzahl. Darüber hinaus ist aus Sicht der Berechnungen der ausgewählte Zufallswert im Intervall
alpha in[0,1] Es wird mit ziemlicher Sicherheit (innerhalb der Grenzen der Maschinengenauigkeit) eine irrationale Zahl sein und ist daher eine gute Wahl für eine Sequenz mit geringer Divergenz. Zur visuellen Lesbarkeit zeigt die obige Abbildung nicht die Ergebnisse der Niederreiter-Sequenz, da sie praktisch nicht von den Ergebnissen der Sobol-Sequenzen und zu unterscheiden sind
R . Die in diesem Beitrag verwendeten Niederreiter- und Sable-Sequenzen (zusammen mit ihrer optimierten Parameterauswahl) wurden in Mathematica unter Verwendung von "geschlossenen proprietären und vollständig optimierten Generatoren aus der Intel MKL-Bibliothek" in der Dokumentation berechnet.
Quasi zufällige Sequenzen in zwei Dimensionen
Die meisten modernen Methoden zur Konstruktion einer geringen Varianz in höheren Dimensionen werden einfach kombiniert (Komponente für Komponente).
d eindimensionale Sequenzen. Der Kürze halber werden wir in der Post hauptsächlich die Holton-Sequenz [
Holton, 1960 ], die Sable-Sequenz und
d -dimensionale Kronecker-Sequenz.
Die Holton-Sequenz wird mit einfachen erstellt
d verschiedene eindimensionale van der Corpute-Sequenzen, deren Basis für alle anderen einfach ist. Das heißt, es handelt sich um paarweise Coprime-Zahlen. Ohne Zweifel ist die häufigste Option aufgrund ihrer offensichtlichen Einfachheit und Logik die Wahl der ersten
d Primzahlen. Die Verteilung der ersten 625 Punkte, die durch die (2,3) Holton-Sequenz definiert sind, ist in Abbildung 1 dargestellt. Obwohl viele zweidimensionale Holton-Sequenzen ausgezeichnete Quellen für Sequenzen mit geringer Divergenz sind, ist bekannt, dass viele von ihnen sehr problematisch sind und keine geringe Divergenz aufweisen. Zum Beispiel zeigt 3, dass Holtons (11,13) -Sequenz sehr auffällige Linien erzeugt. Es wurden große Anstrengungen unternommen, um Methoden zur Auswahl von Modell- und Problempaaren zu entwickeln.
(p1,p2) . In höheren Dimensionen wird das Problem noch komplizierter.
Bei der Verallgemeinerung auf höhere Dimensionen haben rekursive Kronecker-Methoden noch größere Schwierigkeiten. Obwohl mit
alpha= sqrtp Wenn exzellente eindimensionale Sequenzen erstellt werden, ist es äußerst schwierig, Primzahlenpaare zu finden, die als Grundlage für einen unproblematischen zweidimensionalen Fall dienen können! Es wurde beispielsweise vorgeschlagen, andere bekannte irrationale Zahlen als Problemumgehung zu verwenden
phi, pi,e,... . Sie liefern mäßig akzeptable Ergebnisse, werden jedoch im Allgemeinen nicht verwendet, da sie normalerweise nicht so gut sind wie eine korrekt ausgewählte Holton-Sequenz. Es werden große Anstrengungen unternommen, um diese Degenerationsprobleme zu lösen.
Die vorgeschlagenen Lösungen verwenden Überspringen / Brennen, Springen / Ausdünnen. Und zum Codieren (Verwürfeln) der endgültigen Sequenzen wird eine andere Technik verwendet, die häufig verwendet wird, um dieses Problem zu überwinden. Scrambling kann nicht verwendet werden, um eine offene (unendliche) Sequenz mit geringer Divergenz zu erstellen.
Abbildung 3. Die (11,13) -Holton-Sequenz ist offensichtlich keine Sequenz mit geringer Divergenz (links). Es ist auch keine additive rekursive (11,13) Sequenz (in der Mitte). Einige zweidimensionale additive rekursive Sequenzen, die bekannte irrationale Zahlen verwenden, sind ziemlich gut (rechts).In ähnlicher Weise macht die Sable-Sequenz trotz der allgemein besseren Ergebnisse ihre Komplexität und, was noch wichtiger ist, die Notwendigkeit einer sehr sorgfältigen Auswahl von Hyperparametern nicht so freundlich.
Also nochmal in
d Messungen:
- Typische Kronecker-Sequenzen erfordern eine Auswahl d linear unabhängige irrationale Zahlen;
- Holton-Sequenz erfordert d Primzahl paarweise ganze Zahlen; aber
- Die Sable-Sequenz erfordert eine Auswahl d Leitnummern.
Neue Sequenz Rd - der einzige d -dimensionale quasi-zufällige Sequenz mit geringer Divergenz, ohne dass eine Auswahl grundlegender Parameter erforderlich ist.
Verallgemeinerung des Goldenen Schnitts
In diesem Teil werde ich darüber sprechen, wie man eine neue Klasse baut
d -dimensionale offene (unendliche) Sequenz mit geringer Divergenz, die keine Auswahl grundlegender Parameter erfordert, mit hervorragenden Eigenschaften geringer Divergenz.
Es gibt viele Möglichkeiten, die Fibonacci-Sequenz und / oder den Goldenen Schnitt zu verallgemeinern. Die unten vorgeschlagene Methode zur Verallgemeinerung des Goldenen
Schnitts ist nicht neu [
Krchadinac, 2005 ]. Darüber hinaus ist das charakteristische Polynom mit vielen Bereichen der Algebra verbunden, einschließlich
Perron-Zahlen und
Piso-Vijayaraghavan-Zahlen . Neu ist jedoch der explizite Zusammenhang zwischen dieser verallgemeinerten Form und der Konstruktion hochdimensionaler Sequenzen mit geringer Divergenz. Wir definieren eine verallgemeinerte Ansicht des Goldenen Schnitts
phid als einzigartige positive Wurzel
xd+1=x+1 . Also,
Für
d=1 ,
phi1=1.61803398874989484820458683436563... , das ist der kanonische goldene Schnitt.
Für
d=2 ,
phi2=1.32471795724474602596090885447809... . Dieser Wert wird oft als plastische Konstante bezeichnet und hat
schöne Eigenschaften (siehe auch
hier ). Es wird angenommen, dass dieser Wert für das entsprechende zweidimensionale Problem am wahrscheinlichsten optimal ist [
Hensley, 2002 ].
Für
d=3 ,
phi3=1.220744084605759475361685349108831...Für
d>3 Obwohl die Wurzeln dieser Gleichung keine geschlossene algebraische Form haben, können wir leicht eine numerische Näherung erhalten, entweder durch Standardmethoden, zum Beispiel Newtons Methode, oder indem wir dies für die folgende Sequenz notieren
Rd( phid) ::
t0=t1=...=td=1;
tn+d+1=tn+1+tn, quad textrmforn=1,2,3,..
Diese bestimmte Folge von Konstanten
phid wurde 1928 vom Architekten und Mönch Hans van de Laan als "
harmonische Zahlen " bezeichnet. Diese besonderen Bedeutungen können sehr elegant wie folgt ausgedrückt werden:
\ phi_1 = \ sqrt {1+ \ sqrt {1+ \ sqrt {1+ \ sqrt {1+ \ sqrt {1 + ...}}}}
\ phi_2 = \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1 + ...}}}}
\ phi_3 = \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1 + ...}}}}
Wir haben auch die folgende sehr elegante Eigenschaft:
phid= limn to infty fractn+1tn
Diese Sequenz, die manchmal als verallgemeinerte oder verzögerte Fibonacci-Sequenz bezeichnet wird, wurde ziemlich gründlich untersucht [
As, 2004 ,
Wilson, 1993 ] und die Sequenz für
d=2 oft als Padovan-Sequenz bezeichnet [
Stuart, 1996 ,
OEIS A000931 ], und die Sequenz
d=3 aufgeführt in [
OEIS A079398 ]. Wie oben erwähnt, besteht die Hauptaufgabe dieses Beitrags darin, den expliziten Zusammenhang zwischen dieser verallgemeinerten Sequenz und der Konstruktion zu beschreiben
d -dimensionale Sequenzen mit geringer Divergenz.
Hauptergebnis: die folgenden nichtparametrischen d -dimensionale offene (unendliche) Sequenz Rd( phid) weist im Vergleich zu anderen existierenden Verfahren ausgezeichnete Eigenschaften mit geringer Diskrepanz auf.
\ mathbf {t} _n = \ {n \ pmb {\ alpha} \}, \ quad n = 1,2,3, ...
textrmwhere quad pmb alpha=( frac1 phid, frac1 phi2d, frac1 phi3d,... frac1 phidd)
textrmund phid textrmisteineeindeutigepositiveWurzelxd+1=x+1
Für zwei Dimensionen gilt diese verallgemeinerte Reihenfolge für
n=150 Die Punkte sind offensichtlich viel gleichmäßiger verteilt
R2 -Sequenzen als in (2, 3) -Holton-Sequenzen, Kronecker-Sequenzen basierend auf
( sqrt3, sqrt7) , Niederreiter und Sable Sequenzen. (Aufgrund der Komplexität der Niederreiter- und Sable-Sequenzen wurden sie in Mathematica unter Verwendung eines von Intel bereitgestellten proprietären Codes berechnet.) Dies ist die Art der Sequenz, in der der Basisvektor verwendet wird
pmb alpha ist eine Funktion eines einzelnen materiellen Wertes, der oft als Korobov-Sequenz bezeichnet wird [Korobov, 1959]
Schauen Sie sich noch einmal Abbildung 1 an, um verschiedene zweidimensionale quasi zufällige Sequenzen mit geringer Divergenz zu vergleichen.Code und Demos
In einer Dimension Pseudocode für
n Mitglied (
n = 1,2,3, ....) ist definiert als
g = 1.6180339887498948482 a1 = 1.0/g x[n] = (0.5+a1*n) %1
In zwei Dimensionen der Pseudocode für die Koordinaten
x und
yn Mitglied (
n = 1,2,3, ....) sind definiert als
g = 1.32471795724474602596 a1 = 1.0/g a2 = 1.0/(g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1
Pseudocode in drei Dimensionen für Koordinaten
x ,
y und
zn Mitglied (
n = 1,2,3, ....) ist definiert als
g = 1.22074408460575947536 a1 = 1.0/g a2 = 1.0/(g*g) a3 = 1.0/(g*g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1 z[n] = (0.5+a3*n) %1
Python-Code-Vorlage. (Beachten Sie, dass Python-Arrays und -Schleifen von vorne beginnen!)
import numpy as np
Ich habe den Code so geschrieben, dass er der in diesem Beitrag verwendeten mathematischen Notation entspricht. Aus Gründen der Programmierkonventionen und / oder der Effizienz sind jedoch einige Änderungen erwähnenswert. Erstens seit
R2 ist eine additive
rekursive Sequenz, alternative Formulierung
z Dies erfordert keine Gleitkomma-Multiplikation und behält eine hohe Genauigkeit für sehr große Werte bei
n hat die Form
z[i+1] = (z[i]+alpha) %1
Zweitens kann in Sprachen, die vektorisieren können, der Code einer Bruchfunktion wie folgt vektorisiert werden:
for i in range(n): z[i] = seed + alpha*(i+1) z = z %1
Schließlich können wir diese Additionen von Gleitkomma- und Ganzzahlzahlen ersetzen, indem wir alle Konstanten mit multiplizieren
232 und dann die frac (.) Funktion entsprechend ändern. Hier sind die Quellcode-Demos, die von anderen Personen basierend auf dieser Sequenz erstellt wurden:
Mindestverpackungsabstand
Neu R2 -Sequenz ist die einzige zweidimensionale quasi-zufällige Sequenz mit einer geringen Divergenz, bei der der minimale Packungsabstand nur auf reduziert wird 1/ sqrtn .
Obwohl die technische Standardanalyse der Diskrepanzberechnung zu
d∗ - Diskrepanzen, wir werden zunächst einige andere geometrische (und vielleicht viel intuitivere!) Möglichkeiten erwähnen, um zu demonstrieren, wie sehr die neue Sequenz anderen Standardmethoden vorzuziehen ist. Wenn wir den Abstand zwischen Punkten bezeichnen
i und
j für
dij und
d0= textrminfdij dann zeigt die folgende Tabelle, wie es variiert
d0(n) für
R -Sequenzen, (2,3) - Holton-, Sable-, Niederreiter-Sequenzen und Zufallssequenzen. Dies ist in Abbildung 6 zu sehen.
Wie in der vorherigen Abbildung wird der Mindestabstandswert durch den Koeffizienten normalisiert
1/ sqrtn . Sie können das nach bemerken
n=300 Punkte in zufälliger Reihenfolge (grün) erscheinen mit ziemlicher Sicherheit zwei Punkte, die extrem nahe beieinander liegen. Es ist auch zu sehen, dass Holtons (2,3) -Sequenz zwar viel besser ist als die Zufallsstichprobe, aber leider auch asymptotisch auf Null abfällt. Für die Sable-Sequenz sinkt der Grund für die Normalisierung auf Null
d0 liegt in der Tatsache, dass
Sable selbst gezeigt hat, dass
die Sable- Sequenz mit einer Geschwindigkeit abfällt
/n - was gut ist, aber offensichtlich viel schlimmer als
R2 was nur um abnimmt
1/ sqrtn .
Für die Reihenfolge
R( phi2) (blau) Der Mindestabstand zwischen zwei Punkten fällt ständig in das Intervall von
0.549/ sqrtn vorher
0.868/ sqrtn . Beachten Sie, dass der optimale Durchmesser von 0,868 einem Packungsfaktor von 59,2% entspricht. Vergleichen Sie dies mit anderen
Packungen von Kreisen .
Beachten Sie auch, dass
Bridson Poisson Disc Sampling , das
nicht erweiterbar ist
n und wird normalerweise standardmäßig empfohlen, es entsteht immer noch ein Verpackungsfaktor von 49,4%. Es ist erwägenswert, dass das Konzept
d0 bindet Sequenzen fest
phid geringe Diskrepanz mit schlecht approximierbaren Zahlen / Vektoren in
d Messungen [
Hensley, 2001 ]. Obwohl wir wenig über schlecht approximierbare Zahlen in zwei Dimensionen wissen, ist die Konstruktion
phid kann uns einen neuen Blick auf schlecht annähernde Zahlen in höheren Dimensionen geben.
Abbildung 4. Minimaler paarweiser Abstand für verschiedene Sequenzen mit geringer Divergenz. Beachten Sie das R2 - Die Reihenfolge (blau) ist immer die beste Option. Darüber hinaus ist dies die einzige Sequenz, in der der normalisierte Abstand bei nicht gegen Null tendiert n rightarrow infty . Holtons Sequenz (orange) nimmt den zweiten Platz ein, und die Sequenzen Sable (grün) und Niederreiter (rot) sind nicht so gut, aber immer noch viel besser als zufällig (lila). Je größer, desto besser, denn dies entspricht einem längeren Verpackungsabstand.Voronoi-Diagramme
Eine andere Möglichkeit, die gleichmäßige Verteilung von Punkten zu visualisieren, besteht darin, von Anfang an ein Voronoi-Diagramm zu erstellen
n Punkte einer zweidimensionalen Sequenz mit anschließender Färbung jedes Bereichs in Abhängigkeit von seinem
Bereich . Die folgende Abbildung zeigt die Voronoi-Farbkarten für (i)
R2 -folgen; (ii) (2,3) Holton-Sequenzen, (iii) Primrekursion; und (iv) einfache Zufallsstichprobe. Für alle verwendeten Figuren die gleiche Farbskala. Auch hier ist es offensichtlich, dass
R2 Die Sequenz bietet eine viel gleichmäßigere Verteilung als die Holton-Sequenz oder einfache Zufallsstichproben. Das Bild ist das gleiche wie oben, nur entsprechend der Anzahl der Eckpunkte in jeder Voronoi-Zelle gefärbt. Das ist hier nicht nur offensichtlich
R - Die Sequenz bietet eine gleichmäßigere Verteilung als Holton oder einfache Zufallsstichproben, aber die Tatsache, dass Schlüsselwerte deutlicher erkennbar sind
n bestehen nur aus Sechsecken! Wenn wir die verallgemeinerte Fibonacci-Sequenz betrachten, dann
A1=A2=A3=1; quadAn+3=An+1+An . Also
An ::
$$ display $$ \ begin {array} {r} 1 & 1 & 1 & 2 & 2 & 3 & 4 & 5 & 7 \\ 9 & \ textbf {12} & 16 & 21 & 28 & 37 & \ textbf {49} & 65 & 86 \\ 114 & \ textbf {151 } & 200 & 265 & 351 & 465 & \ textbf {616} & 816 & 1081 \\ 1432 & \ textbf {1897} & 2513 & 3329 & 4410 & 5842 & \ textbf {7739} & 10252 & 13581 \\ 17991 & \ textbf {23833} & 31572 & 41824 & 55405 & 7 {97229} & 128801 & 170625 \\ 226030 & \ textbf {299426} & 396655 & 525456 & 696081 & 922111 & \ textbf {1221537} & 1618192 & 2143648 \\ \ end {array} $$ display $$
Alle Werte in denen
n=A9k−2 oder
n=A9k+2 bestehen nur aus Sechsecken.
Abbildung 4. Visualisierung der Form von Voronoi-Diagrammen basierend auf der Fläche jedes Voronoi-Polygons für (i) R2 -folgen; (ii) (2,3) -Sequenzen basierend auf Primzahlen; (iii) die (2,3) -Sequenz von Holton, (iv) Niederraiter; (v) Zobel; und (iv) einfache Zufallsstichprobe. Farben geben die Anzahl der Seiten jedes Voronoi-Polygons an. Ich wiederhole: Es ist offensichtlich, dass R( phi) -Sequenz bietet eine viel gleichmäßigere Verteilung als jede andere Sequenz mit geringer Divergenz.Bei bestimmten Werten n Voronoi Gitter für R2 -Sequenz besteht nur aus Sechsecken.
Abbildung 5. Visualisierung der Form von Voronoi-Diagrammen basierend auf der Anzahl der Seiten jedes Voronoi-Polygons für (i) R2 -folgen; (ii) (2,3) -Sequenzen basierend auf Primzahlen; (iii) die (2,3) -Sequenz von Holton, (iv) Niederraiter; (v) Zobel; und (iv) einfache Zufallsstichprobe. Farben geben die Anzahl der Seiten jedes Voronoi-Polygons an. Ich wiederhole: Es ist offensichtlich, dass R( phi) -Sequenz bietet eine viel gleichmäßigere Verteilung als jede andere Sequenz mit geringer Divergenz.Delaunay quasi zufällige Kacheln für ein Flugzeug
R -sequence ist die einzige quasi zufällige Sequenz mit geringer Divergenz, die zum Erstellen verwendet werden kann d -dimensionale quasiperiodische Fliesen mit seinem Delaunay-Netz.
Die Delaunay-Triangulation, die Graf Voronoi ähnelt, bietet die Möglichkeit, diese Verteilungen unterschiedlich zu betrachten. Noch wichtiger ist jedoch, dass die Delaunay-Triangulation eine neue Methode zum Erstellen einer quasiperiodischen Kachelung (Mosaikkachelung) einer Ebene bietet. Delaunay-Triangulation
R2 -Sequenzen liefert ein viel einheitlicheres Muster als eine Holton-Sequenz oder eine Zufallsstichprobe. Insbesondere wenn eine Delaunay-Triangulation von Punktverteilungen durchgeführt wird, wobei
n gleich einer der verallgemeinerten Fibonacci-Sequenzen:
AN=$1,1,1,2,3,4,5,7,9,12,16,21,28,37,... dann besteht die Delaunay-Triangulation nur aus drei identisch gepaarten Dreiecken, dh aus Parallelogrammen (Rhomboiden)! (Mit Ausnahme von Dreiecken, die einen gemeinsamen Scheitelpunkt mit einer konvexen Hülle haben.)
Bei Werten n=Ak Delaunay-Triangulation R2 -Sequenzen bilden quasiperiodische Kacheln, von denen jedes nur aus drei Grunddreiecken (rot, gelb, blau) besteht, die immer paarweise verbunden sind und mit drei Parallelogrammen (Rhomboiden) eine genau definierte quasiperiodische Kachelung (Kachelung) der Ebene bilden.
Abbildung 6. Visualisierung der Delaunay-Triangulation für (i) R( phi2) -folgen; (ii) (2,3) Holton-Sequenzen, (iii) Primrekursion; und (iv) einfache Zufallsstichprobe. Farben geben die Fläche jedes Dreiecks an. Alle vier Diagramme verwenden denselben Maßstab. Und auch hier ist es offensichtlich, dass R( phi2) -Sequenz bietet eine viel gleichmäßigere Verteilung als jede andere Sequenz mit geringer Divergenz.Beachten Sie das
R2 basierend auf
phi2=1.32471795724474602596 die kleinste Anzahl von Piso sein, (a
phi=1.61803... Ist die größte Anzahl von Pisos). Die Verbindung von quasiperiodischen Kacheln mit quadratischen und kubischen Zahlen von Piso ist nicht neu [
Elkharrat und Masakova], aber ich glaube, dass zum ersten Mal quasiperiodische Kacheln auf der Grundlage von erstellt wurden
phi2=1.324719... .
Die folgende Animation zeigt, wie das Delaunay-Netz für die Sequenz ineinander greift
R2 ändert sich mit der schrittweisen Hinzufügung von Punkten. Beachten Sie, dass, wenn die Anzahl der Punkte einem Mitglied der verallgemeinerten Fibonacci-Sequenz entspricht, das gesamte Delaunay-Gitter nur aus roten, blauen und gelben Parallelogrammen (Rhomboiden) besteht, die in einer doppelten quasiperiodischen Form angeordnet sind.
Obwohl die Anordnung der roten Parallelogramme eine beträchtliche Regelmäßigkeit zeigt, kann man deutlich sehen, dass die blauen und gelben Parallelogramme in einer quasiperiodischen Form vorliegen. Das Fourier-Spektrum dieses Gitters ist in Abbildung 11 zu sehen und repräsentiert die klassischen Punktspektren. (Beachten Sie, dass eine auf Primzahlen basierende rekursive Sequenz auch in dem Sinne quasiperiodisch erscheint, dass es sich um ein geordnetes, sich nicht wiederholendes Muster handelt. Ihr Muster jedoch im Intervall
n nicht so konstant und hängt auch entscheidend von der Wahl der Grundparameter ab. Daher werden wir unser Interesse an quasiperiodischen Fliesen nur nach der Reihenfolge konzentrieren
R2 .) Es besteht nur aus drei Dreiecken: rot, gelb, blau. Beachten Sie dies in dieser Reihenfolge
R( phi2) Alle Parallelogramme jeder Farbe haben die gleiche Größe und Form. Das Seitenverhältnis dieser einzelnen Dreiecke ist unglaublich elegant. Nämlich
textrmFläche(rot):Fläche(gelb):Fläche(blau)=1: phi2: phi22
Gleiches gilt für die relative Häufigkeit von Dreiecken:
f( textrmrot):f( textrmgelb):f( textrmblau)=1: phi2:1
Daraus folgt, dass die gesamte relative Fläche, die von diesen drei Dreiecken im Raum abgedeckt wird, ist:
f( textrmrot):f( textrmgelb):f( textrmblau)=1: phi22: phi22
Es kann auch angenommen werden, dass wir diese quasiperiodische Kachelung durch Substitution basierend auf der Sequenz A erzeugen können
A rightarrowB; quadB rightarrowC; quadC rightarrowBA
Wenn wir für drei Dimensionen die verallgemeinerte Fibonacci-Sequenz betrachten, dann
B1=B2=B3=B4=1; quadBn+4=Bn+1+Bn . Also
B_n = \ {1,1,1,1,2,2,2,3,4,4,5,7,8,9,12,15,17,21,27,32,38,48,59 , 70,86,107,129, ...
Bei bestimmten Werten n=Bk 3D-Delaunay-Netz, das einer Sequenz zugeordnet ist R3 definiert ein quasiperiodisches Kristallgitter.
Diskretisierte Verpackung, Teil 2
Die folgende Abbildung zeigt die erste
n=2500 Punkte für jede zweidimensionale Sequenz mit geringer Divergenz. Darüber hinaus ist jede der Zellen 50 × 50 = 2500 nur dann grün gefärbt, wenn sie
genau 1 Punkt enthält. Das heißt, je mehr grüne Quadrate vorhanden sind, desto gleichmäßiger ist die Verteilung von 2500 Punkten in 2500 Zellen. Der Prozentsatz an grünen Zellen für jede der Figuren ist wie folgt:
R2 (75%), Holton (54%), Kronecker (48%), Niederreiter (54%), Sable (49%) und zufällig (38%).
Schallwellen
Nur zum Spaß habe ich auf Wunsch
eines News Hacker-Lesers modelliert, wie all diese quasi zufälligen Punktverteilungen
klingen können ! Ich habe die Listplay-Funktion von Mathematica verwendet: "
ListPlay [{a1, a2, ...}] erstellt ein Objekt, das sich selbst als Klang reproduziert und dessen Amplitude als Folge von Pegeln angegeben wird." Daher werde ich Sie ohne Kommentare selbst entscheiden lassen, welche Ihnen unter den eindimensionalen Quasi-Zufallsverteilungen (Mono) und zweidimensionalen Quasi-Zufallsverteilungen (Stereo) am besten gefällt.
| Mono | Stereo |
|---|
| Zufällig | | |
| Sable | | |
| Niederreiter | | |
| Holton | | |
| Kronecker | | |
| R. | | |
Multiklassen-Sets mit geringer Diskrepanz
Einige Sequenzen mit geringer Divergenz zeigen, was als "Mehrklassen-Divergenz mit geringer Divergenz" bezeichnet wird. Bis zu diesem Moment gingen wir davon aus, dass wir uns so gleichmäßig wie möglich verteilen müssen
n Punkte, dann sind alle Punkte gleich und nicht voneinander zu unterscheiden. In vielen Situationen gibt es jedoch verschiedene Arten von Punkten. Wir betrachten das Problem der gleichmäßigen Verteilung
n so dass nicht nur alle Punkte gleichmäßig verteilt sind, sondern auch Punkte derselben Klasse. Nehmen wir insbesondere an, dass es solche gibt
nk Punkte eingeben
k , (wo
n1+n2+n3+...+nk=n ), dann ist die Verteilung des Multisets mit einer niedrigen Verteilung eine Verteilung, in der jeder
nk Punkte gleichmäßig verteilt. In unserem Fall haben wir das gefunden
R -Die Holton-Sequenz und -Sequenz lässt sich leicht an Sequenzen von Multisets mit geringer Divergenz anpassen, indem einfach abwechselnd Punkte jedes Typs platziert werden.
Die folgende Abbildung zeigt, wie sie verteilt sind
n=150 Punkte, während 75 blau, 40 pfefferig, 25 grün und 10 rot sind. Für eine additive rekursive Sequenz ist dies trivial gelöst: Die ersten 75 Mitglieder entsprechen einfach Blau, die nächsten 40 Orange, die nächsten 25 Grün und die letzten 10 Rotpunkte. Diese Technik funktioniert fast für Holton- und Kronecker-Sequenzen, ist jedoch in den Niederreiter- und Sable-Sequenzen sehr schlecht. Darüber hinaus sind keine Techniken zur kontinuierlichen Erzeugung von Punktverteilungen mit mehreren Skalen in den Niederreiter- und Sable-Sequenzen bekannt. Dies zeigt, dass
Verteilungen von Mehrklassenpunkten , wie beispielsweise den
Augen von Hühnern , nun direkt unter Verwendung von Sequenzen mit geringer Divergenz beschrieben und konstruiert werden können.
Sequenz R2 Ist eine quasi zufällige Sequenz mit geringer Divergenz, die eine einfache Konstruktion einer Mehrfachdivergenz mit geringer Divergenz ermöglicht.
Abbildung 9. Multiskalensequenzen mit geringer Divergenz. Nacheinander R Nicht nur alle Punkte sind gleichmäßig verteilt, sondern auch die Punkte jeder einzelnen Farbe.Quasi zufällige Punkte auf einer Kugel
In den Bereichen Computergrafik und Physik ist es häufig erforderlich, Punkte auf der Oberfläche einer dreidimensionalen Kugel so gleichmäßig wie möglich zu verteilen. Bei Verwendung offener (unendlicher) quasi-zufälliger Sequenzen wird dieses Problem nur dadurch reduziert, dass quasi-zufällige Punkte unter Verwendung der Lambert-Gleichprojektion gleichmäßig in einem Einheitsquadrat auf der Oberfläche der Kugel verteilt werden. Lambert Standardprojektionstransformation Platzieren eines Punktes
(u,v) inU[0,1] bis(x,y,z) inS2 hat die Form:
(x,y,z)=( cos lambda cos phi, cos lambda sin phi, sin lambda)
textrmwhere quad cos( lambda− pi/2)=(2u−1); quad phi=2 piv
Seitdem
phi2 -Die Sequenz ist vollständig geöffnet und ermöglicht es Ihnen, eine unendliche Folge von Punkten Punkt für Punkt auf der Oberfläche der Kugel zu fangen. Dies steht im Gegensatz zu anderen Methoden wie dem
Gitter der Fibonacci-Spirale , bei denen die Anzahl der Punkte im Voraus bekannt sein muss. Bei der Sichtprüfung können wir das wieder deutlich erkennen
n=1200 neu
R( phi2) - Die Sequenz ist viel besser verteilt als die Holton-Überlagerung oder die Kronecker-Stichprobe, die wiederum viel gleichmäßiger ist als die Zufallsstichprobe.
Abbildung 10Computergrafik-Dithering
Die meisten modernen Dithering-Techniken (z. B. Floyd-Steinberg-Dithering) basieren auf der Fehlerverteilung, die für die parallele Verarbeitung und / oder direkte Optimierung in der GPU nicht sehr geeignet ist. In solchen Fällen zeigt das Punktdithering mit statischen Dithermasken (d. H. Vollständig abhängig vom Zielbild) ausgezeichnete Leistungseigenschaften. Die wahrscheinlich bekanntesten und am weitesten verbreiteten Dithering-Masken basieren auf
Bayer- Matrizen, aber neuere versuchen, die Eigenschaften des blauen Rauschens näher zu simulieren. Die nicht triviale Schwierigkeit beim Erstellen von Dither-Masken basierend auf Sequenzen mit geringer Divergenz und / oder blauem Rauschen besteht darin, dass diese Sequenzen mit geringer Divergenz eine Ganzzahl projizieren
Z zu einem zweidimensionalen Punkt im Intervall
[0,1)2 .
Für eine Dithering-Maske ist jedoch eine Funktion erforderlich, die die zweidimensionalen Ganzzahlkoordinaten der gerasterten Maske in den tatsächlichen Helligkeits- / Schwellenwert im Intervall projiziert [0,1) .
Ich schlage den folgenden Ansatz vor, der auf basiert RFolgen. Für jedes Pixel (x, y) in der Maske weisen wir seinen Helligkeitswert zuI(x,y) wo:I(x,y)=α1x+α2y(mod1);
αα=(α1,α2)=(1ϕ2,1ϕ22)
ϕ2 - x3=x+1
Also x=1.32471795724474602596… was bedeutetα1=0.75487766624669276;α2=0.569840290998
Wenn außerdem eine Dreieckswellenfunktion hinzugefügt wird, um die durch die frac (.) -Funktion verursachte Diskontinuität an jeder ganzzahligen Grenze zu beseitigen:T(z)={2z,if 0≤z<1/22−2z,if1/2≤z<1
I(x,y)=T[α1x+α2y(mod1)];
dann werden die Maske und ihr Fourier / Frequenz-Diagramm weiter verbessert. Wir stellen auch fest, dass seitdemlimn→∞AnAn+1=0.754878;limn→∞AnAn+2=0.56984
dann bezieht sich die Form des obigen Ausdrucks auf die folgende kongruente GleichungDithering-R-Masken erzeugen Ergebnisse, die mit modernen Methoden auf der Basis von Blue-Noise-Masken konkurrieren. Im Gegensatz zu Masken mit blauem Rauschen müssen sie jedoch nicht im Voraus berechnet werden, da sie in Echtzeit berechnet werden können.
Es ist erwähnenswert, dass diese Struktur auch von Mittring vorgeschlagen wurde , er jedoch die Koeffizienten empirisch findet (und die Endwerte nicht reproduziert). Darüber hinaus hilft es zu verstehen, warum die empirische Formel von Jorge Jimenez , mit der „Call of Duty“ (oft als „Interleaved Gradient Noise“ bezeichnet) erstellt wurde, so gut funktioniert .Es sind jedoch 3 Gleitkomma-Multiplikationen und zwei% 1-Operatoren erforderlich, und die vorherige Formel zeigt, dass dies mit nur zwei Gleitkomma-Multiplikationen und einer% 1-Operation möglich ist. Noch wichtiger ist jedoch, dass dieser Beitrag ein klareres mathematisches Verständnis dafür liefert, warum eine Dither-Maske in dieser Form so effektiv, wenn nicht sogar optimal ist. Die Ergebnisse dieser Dithering-Matrix werden unten am Beispiel des klassischen Lena 256 × 256-Testbilds sowie eines Schachtestmusters gezeigt. Es zeigt auch die Ergebnisse der Verwendung von Standard-Bayer-Dithering-Masken sowie ein Beispiel mit blauem Rauschen. Die beiden häufigsten Methoden für blaues Rauschen sind Void-and-Cluster- und Poisson-Disc-Sampling. Der Kürze halber habe ich nur die Ergebnisse der Void- und Cluster-Methode gezeigt. [ Peters]. Interleaved Gradient Noise funktioniert besser als Bayer und Blue Noise, aber nicht so gut wieZittern. Sie können sehen, dass das Bayer-Dithering in hellgrauen Bereichen eine merkliche Dissonanz von Weiß zeigt. Zittern- Sequenz und blaues Rauschen sind im Allgemeinen vergleichbar, obwohl geringfügige Unterschiede erkennbar sind. Es ist erwähnenswert, einige Aspekte des R-Dithering zu beachten:- Er ist nicht isotrop! Fourierspektren zeigen nur einzelne und diskrete Punkte. Dies ist ein klassisches Merkmal von quasiperiodischen Fliesen und Beugungsspektren von Quasikristallen. Insbesondere die Fourier-Spektren für -Masken entsprechen der Tatsache, dass die Delaunay-Triangulation für die kanonische R-Sequenz aus einer quasiperiodischen Kachelung von drei Parallelogrammen besteht.
- R-Dithering in Kombination mit einer Dreieckswelle ergibt eine unglaublich gleichmäßige Maske!
- R- , .
- , , R- , .
- , .
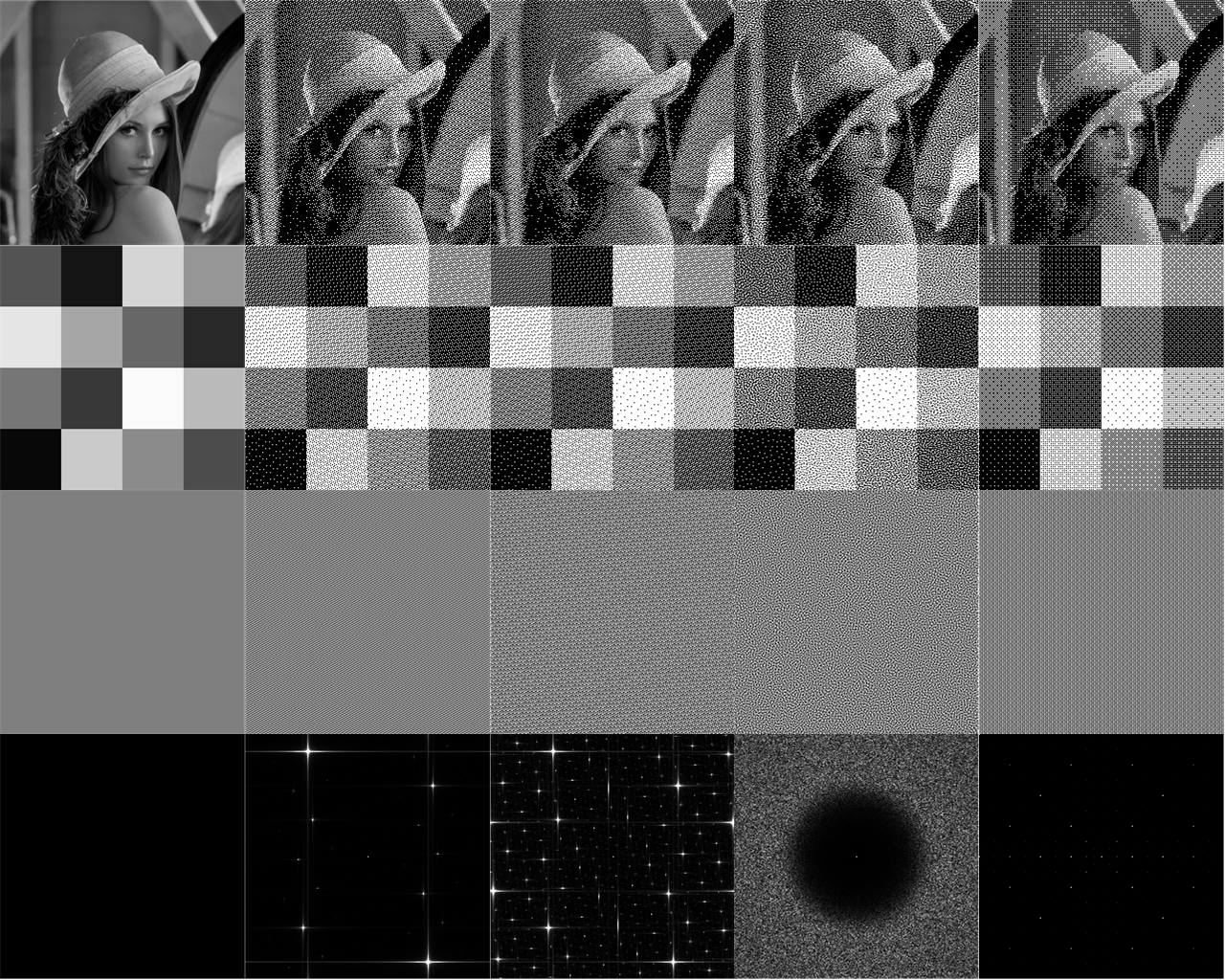
Höhere Dimensionen
Ähnlich wie im vorherigen Abschnitt, jedoch für fünf (5) Messungen, zeigt die folgende Grafik den (globalen) Mindestabstand zwischen zwei beliebigen Punkten für -Sequenzen, (2,3,5,7,11) -Holtonsequenzen und Zufallssequenzen. Diesmal wird der normalisierte Wert des Mindestabstands um einen Faktor normalisiert .
Sie können sehen, dass die Zufallsverteilung aufgrund des „Fluches der Dimensionen“ besser ist als alle Sequenzen mit geringer Divergenz - mit Ausnahme von Folgen. In
-folgen auch mit Punkte ist der Mindestabstand zwischen zwei Punkten immer noch nahe und immer höher .
Sequenz - der einzige -dimensionale Sequenz mit geringer Divergenz, bei der der Verpackungsabstand nur mit der Geschwindigkeit zu sinken beginnt .
Abbildung 12. Dies zeigt, dass die R-Sequenz (blau) durchweg besser ist als Holton (orange). Sable (grün); Niederreiter (rot); und zufällig (lila). Beachten Sie, dass je größer desto besser, da dies einem längeren Verpackungsabstand entspricht.Numerische Integration
Die folgende Grafik zeigt typische Fehlerkurven. ein bestimmtes Integral zu approximieren, das einer Gaußschen Funktion halber Breite zugeordnet ist ,
während: (i) (blau); (ii) Holton-Sequenz (orange); (iii) zufällig (grün); (iv) Zobel (rot). Die Grafik zeigt, dass fürEs gibt jetzt weniger Unterschiede zwischen der Zufallsstichprobe und der Holton-Sequenz. Wie jedoch im eindimensionalen Fall gezeigt wurde,- Sequenz und Sable sind immer besser als Holtons Sequenz. Es lässt uns auch wissen, dass die Sequenz von Sable etwas besser ist. Folgen.Figure 13. Monte-Carlo-Quasi-Zufallsmethoden für die 8-dimensionale Integration. Je niedriger der Wert, desto besser. Die neue R-Sequenz und Sable-Sequenz zeigen sich viel besser als die Holton-Sequenz.