Relationale Programmierung: Schmerz, Interesse und wieder Schmerz

Im vorherigen Beitrag haben wir ausführlich erklärt, was wir Studenten im Bereich "Industrielle Programmierung" beibringen. Für diejenigen, deren Interessengebiet in einem eher theoretischen Bereich liegt, beispielsweise durch neue Programmierparadigmen oder abstrakte Mathematik, die in der theoretischen Programmierforschung verwendet werden, gibt es eine weitere Spezialisierung - „Programmiersprachen“.

Heute werde ich über meine Forschung auf dem Gebiet der relationalen Programmierung sprechen, die ich an der Universität und als studentischer Forscher im Labor für Sprachwerkzeuge JetBrains Research mache.

Was ist relationale Programmierung? Normalerweise führen wir eine Funktion mit Argumenten aus und erhalten das Ergebnis. Und im relationalen Fall können Sie das Gegenteil tun: Korrigieren Sie das Ergebnis und ein Argument und erhalten Sie das zweite Argument. Die Hauptsache ist, den Code richtig zu schreiben, geduldig zu sein und einen guten Cluster zu haben.

Über mich

Mein Name ist Dmitry Rozplokhas, ich bin ein Erstsemester der HSE in St. Petersburg und habe letztes Jahr das Bachelor-Programm der Akademischen Universität im Bereich „Programmiersprachen“ abgeschlossen. Seit dem dritten Studienjahr bin ich auch Forschungsstudent im JetBrains Research-Labor für Sprachwerkzeuge.

Relationale Programmierung

Allgemeine Fakten

Relationale Programmierung ist, wenn Sie anstelle von Funktionen die Beziehung zwischen Argumenten und dem Ergebnis beschreiben. Wenn die Sprache dafür geschärft ist, können Sie bestimmte Boni erhalten, z. B. die Möglichkeit, die Funktion in die entgegengesetzte Richtung auszuführen (stellen Sie dadurch die möglichen Werte der Argumente wieder her).

Im Allgemeinen kann dies in jeder logischen Sprache erfolgen, aber das Interesse an relationaler Programmierung entstand gleichzeitig mit dem Aufkommen einer minimalistischen rein logischen Sprache miniKanren vor etwa zehn Jahren, die es ermöglichte, solche Beziehungen bequem zu beschreiben und zu verwenden.

Hier sind einige der fortschrittlichsten Anwendungsfälle: Sie können einen Proof Checker schreiben und ihn verwenden, um Beweise zu finden ( Near et al., 2008 ) oder einen Interpreter für eine bestimmte Sprache erstellen und damit Testsuite-Programme generieren ( Byrd et al., 2017 ).

Syntax- und Spielzeugbeispiel

miniKanren ist eine kleine Sprache, zur Beschreibung von Beziehungen werden nur grundlegende mathematische Konstruktionen verwendet. Dies ist eine eingebettete Sprache, ihre Grundelemente sind eine Bibliothek für eine externe Sprache, und kleine miniKanren-Programme können innerhalb eines Programms in einer anderen Sprache verwendet werden.

Fremdsprachen geeignet für miniKanren, eine ganze Reihe. Ursprünglich gab es Schema, wir arbeiten mit der Version für Ocaml ( OCanren ), und die vollständige Liste kann auf minikanren.org eingesehen werden . Beispiele in diesem Artikel beziehen sich auch auf OCanren. Viele Implementierungen fügen Hilfsfunktionen hinzu, aber wir werden uns nur auf die Kernsprache konzentrieren.

Beginnen wir mit den Datentypen. Herkömmlicherweise können sie in zwei Typen unterteilt werden:

• Konstanten sind einige Daten aus der Sprache, in die wir eingebettet sind. Zeichenfolgen, Zahlen, sogar Arrays. Für die grundlegenden miniKanren ist dies jedoch alles eine Blackbox. Konstanten können nur auf Gleichheit überprüft werden.
  
• Ein "Begriff" ist ein Tupel aus mehreren Elementen. Wird häufig wie Datenkonstruktoren in Haskell verwendet: Datenkonstruktor (Zeichenfolge) plus null oder mehr Parameter. OCanren verwendet reguläre Datenkonstruktoren von OCaml.
  

Wenn wir beispielsweise mit Arrays in miniKanren selbst arbeiten möchten, muss dies in Begriffen beschrieben werden, die funktionalen Sprachen ähnlich sind - als einfach verknüpfte Liste. Eine Liste ist entweder eine leere Liste (angezeigt durch einen einfachen Begriff) oder ein Paar aus dem ersten Element der Liste („Kopf“) und den verbleibenden Elementen („Schwanz“).

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil))) 

Ein miniKanren-Programm ist die Beziehung zwischen einigen Variablen. Beim Start gibt das Programm alle möglichen Werte der Variablen in allgemeiner Form an. Bei Implementierungen können Sie häufig die Anzahl der Antworten in der Ausgabe begrenzen, z. B. nur die erste finden. Die Suche wird nicht immer beendet, nachdem alle Lösungen gefunden wurden.

Sie können mehrere Beziehungen schreiben, die durch einander definiert und sogar rekursiv als Funktionen aufgerufen werden. Zum Beispiel unten wir statt Funktion $$$append (a, b) → mit$Definieren Sie die Beziehung $$$appendo (a, b, c)$: Liste $$$c$ist eine Verkettung von Listen $$$a$und $$$b$. Funktionen, die Beziehungen zurückgeben, enden traditionell mit einem „o“, um sie von normalen Funktionen zu unterscheiden.

Eine Beziehung wird als eine Aussage bezüglich ihrer Argumente geschrieben. Wir haben vier grundlegende Operationen :

• Vereinheitlichung oder Gleichheit (===) zweier Begriffe, Begriffe können Variablen enthalten. Sie können beispielsweise die Relationsliste schreiben $$$l$besteht aus einem Element $$$x$":
  
  

   let isSingletono xl = l === Cons (x, Nil) 

• Konjunktion (logisches „und“) und Disjunktion (logisches „oder“) - wie in der normalen Logik. OCanren werden als &&& und ||| bezeichnet. Grundsätzlich gibt es in MiniKanren keine logische Ablehnung.
  
• Neue Variablen hinzufügen. In der Logik ist es ein Quantifizierer der Existenz. Um beispielsweise die Liste auf Nicht-Leere zu überprüfen, müssen Sie überprüfen, ob die Liste aus einem Kopf und einem Schwanz besteht. Sie sind keine Argumente der Beziehung, daher müssen Sie neue Variablen erstellen:
  
  

   let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 

Eine Beziehung kann sich rekursiv aufrufen. Beispielsweise müssen Sie das Element "Beziehung" definieren $$$x$liegt auf der Liste. " Wir werden dieses Problem lösen, indem wir triviale Fälle wie in funktionalen Sprachen analysieren:

1. Oder der Kopf der Liste ist $$$x$
   
2. Entweder $$$x$liegt im Schwanz
   

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) ) 

Die Basisversion der Sprache basiert auf diesen vier Operationen. Es gibt auch Erweiterungen, mit denen Sie andere Vorgänge verwenden können. Am nützlichsten ist die Ungleichheitsbeschränkung zum Festlegen der Ungleichung zweier Terme (= / =).

Trotz des Minimalismus ist miniKanren eine sehr ausdrucksstarke Sprache. Betrachten Sie beispielsweise die relationale Verkettung zweier Listen. Die Funktion zweier Argumente wird zu einer dreifachen Beziehung " $$$ab$ist eine Verkettung von Listen $$$a$und $$$b$".

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb))) 

Die Lösung unterscheidet sich strukturell nicht davon, wie wir sie in einer funktionalen Sprache schreiben würden. Wir analysieren zwei Fälle, die durch eine Klausel vereint sind:

1. Wenn die erste Liste leer ist, sind die zweite Liste und das Ergebnis der Verkettung gleich.
   
2. Wenn die erste Liste nicht leer ist, analysieren wir sie in Kopf und Schwanz und konstruieren das Ergebnis mithilfe eines rekursiven Aufrufs der Beziehung.
   

Wir können eine Anfrage zu dieser Beziehung stellen und das erste und zweite Argument korrigieren - wir erhalten die Verkettung von Listen:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q) 

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil)))) 

Wir können das letzte Argument beheben - wir teilen alle Partitionen dieser Liste in zwei Teile.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil))))) 

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil 

Sie können alles andere tun. Ein etwas ungewöhnlicheres Beispiel, in dem wir nur einen Teil der Argumente korrigieren:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil)))))) 

⇒

 q = 2, r = Cons (3, Cons (4, Nil)) 

Wie funktioniert es?

Aus theoretischer Sicht gibt es hier nichts Beeindruckendes: Sie können jederzeit alle möglichen Optionen nach allen Argumenten durchsuchen und für jede Menge prüfen, ob sie sich in Bezug auf eine bestimmte Funktion / Beziehung so verhalten, wie wir es möchten (siehe "Der Algorithmus des British Museum" ). . Von Interesse ist die Tatsache, dass hier die Suche (mit anderen Worten die Suche nach einer Lösung) nur die Struktur der beschriebenen Beziehung verwendet, wodurch sie in der Praxis relativ effektiv sein kann.

Die Suche bezieht sich auf das Sammeln von Informationen über verschiedene Variablen im aktuellen Zustand. Wir wissen entweder nichts über jede Variable oder wir wissen, wie sie in Begriffen, Werten und anderen Variablen ausgedrückt wird. Zum Beispiel:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

Während der Vereinheitlichung betrachten wir zwei Begriffe unter Berücksichtigung dieser Informationen und aktualisieren entweder den Status oder beenden die Suche, wenn zwei Begriffe nicht vereinheitlicht werden können. Wenn Sie beispielsweise die Vereinigung b = c abschließen, erhalten Sie neue Informationen: x = 10, y = z. Aber die Vereinigung b = Nil wird einen Widerspruch verursachen.

Wir suchen nacheinander in Konjunktionen (so dass sich Informationen ansammeln), und in einer Disjunktion teilen wir die Suche in zwei parallele Zweige auf und gehen abwechselnd in diesen Schritten weiter - dies ist die sogenannte Interleaving-Suche. Dank dieser Abwechslung ist die Suche abgeschlossen - jede geeignete Lösung wird nach einer begrenzten Zeit gefunden. In der Prolog-Sprache ist dies beispielsweise nicht der Fall. Es macht so etwas wie ein tiefes Crawlen (das an einem unendlichen Zweig hängen kann), und das Verschachteln der Suche ist im Wesentlichen eine knifflige Modifikation des breiten Crawls.

Lassen Sie uns nun sehen, wie die erste Abfrage aus dem vorherigen Abschnitt funktioniert. Da Appendo rekursive Aufrufe hat, fügen wir Variablen Indizes hinzu, um sie zu unterscheiden. Die folgende Abbildung zeigt den Aufzählungsbaum. Pfeile geben die Richtung der Verbreitung von Informationen an (mit Ausnahme der Rückkehr von der Rekursion). Zwischen Disjunktionen werden Informationen nicht verteilt, und zwischen Konjunktionen wird von links nach rechts verteilt.

1. Wir beginnen mit einem externen Anruf bei Appendo. Der linke Zweig der Disjunktion stirbt aufgrund von Kontroversen: Liste $$$a$nicht leer.
   
2. Im rechten Zweig werden Hilfsvariablen eingeführt, die dann zum „Parsen“ der Liste verwendet werden $$$a_1$an Kopf und Schwanz.
   
3. Danach erfolgt der Appendo-Rekursionsaufruf für a = [2], b = [3, 4], ab =?, In denen ähnliche Operationen auftreten.
   
4. Aber im dritten Appendo-Aufruf haben wir bereits a = [], b = [3,4], ab =?, Und dann funktioniert die linke Disjunktion einfach, wonach wir die Informationen ab = b erhalten. Aber im rechten Zweig gibt es einen Widerspruch.
   
5. Jetzt können wir alle verfügbaren Informationen aufschreiben und die Antwort wiederherstellen, indem wir die Werte der Variablen ersetzen:
   
   a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4]

   
6. Daraus folgt $$$ab_1$= Nachteile (1, Nachteile (2, [3, 4])) = [1, 2, 3, 4] nach Bedarf.
   

Was ich im Grundstudium gemacht habe

Alles verlangsamt sich

Wie immer: Sie versprechen Ihnen, dass alles sehr aussagekräftig sein wird, aber in Wirklichkeit müssen Sie sich an die Sprache anpassen und alles auf besondere Weise schreiben (unter Berücksichtigung der Art und Weise, wie alles ausgeführt wird), damit zumindest etwas funktioniert, mit Ausnahme der einfachsten Beispiele. Das ist enttäuschend.

Eines der ersten Probleme, mit denen ein unerfahrener miniKanren-Programmierer konfrontiert ist, besteht darin, dass es sehr stark von der Reihenfolge abhängt, in der Sie die Bedingungen (Konjunktionen) im Programm beschreiben. Mit einer Bestellung ist alles in Ordnung, aber zwei Konjunktionen wurden getauscht und alles begann sehr langsam zu arbeiten oder endete überhaupt nicht. Das ist unerwartet.

Selbst im Beispiel mit Appendo endet das Starten in die entgegengesetzte Richtung (Generieren der Aufteilung der Liste in zwei) nur, wenn Sie explizit angeben, wie viele Antworten Sie möchten (die Suche wird beendet, nachdem die erforderliche Anzahl gefunden wurde).

Angenommen, wir fixieren die ursprünglichen Variablen wie folgt: a =?, B =?, Ab = [1, 2, 3] (siehe Abbildung unten). Im zweiten Zweig werden diese Informationen während des rekursiven Aufrufs in keiner Weise verwendet (die Variable ab und Einschränkungen für $$$h_1$und $$$tb_1$erscheinen erst nach diesem Aufruf). Daher sind beim ersten rekursiven Aufruf alle Argumente freie Variablen. Dieser Aufruf generiert alle Arten von Tripeln aus zwei Listen und deren Verkettung (und diese Generation wird niemals enden), und dann werden unter ihnen diejenigen ausgewählt, für die das dritte Element genau so ausfiel, wie wir es brauchen.



Alles ist nicht so schlimm, wie es auf den ersten Blick scheinen mag, weil wir diese Dreiergruppen in großen Gruppen sortieren werden. Listen mit der gleichen Länge, aber unterschiedlichen Elementen unterscheiden sich nicht vom Standpunkt der Funktion, daher fallen sie in eine Lösung - anstelle der Elemente gibt es freie Variablen. Trotzdem werden wir weiterhin alle möglichen Listenlängen sortieren, obwohl wir nur eine benötigen und wissen, welche. Dies ist eine sehr irrationale Verwendung (Nichtverwendung) von Informationen bei der Suche.

Dieses spezielle Beispiel lässt sich leicht beheben: Sie müssen nur den rekursiven Aufruf an das Ende verschieben, und alles funktioniert ordnungsgemäß. Vor dem rekursiven Aufruf findet eine Vereinigung mit der Variablen ab statt, und der rekursive Aufruf erfolgt vom Ende der angegebenen Liste aus (als normale rekursive Funktion). Diese Definition mit einem rekursiven Aufruf am Ende funktioniert in alle Richtungen: Für den rekursiven Aufruf schaffen wir es, alle möglichen Informationen über die Argumente zu sammeln.

In einem etwas komplexeren Beispiel existiert jedoch bei mehreren sinnvollen Aufrufen nicht eine bestimmte Reihenfolge, für die alles in Ordnung ist. Das einfachste Beispiel: Erweitern einer Liste mithilfe von Verkettung. Wir korrigieren das erste Argument - wir brauchen diese bestimmte Reihenfolge, wir korrigieren das zweite - wir müssen die Anrufe tauschen. Andernfalls wird lange gesucht und die Suche wird nicht beendet.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr)) 

Dies liegt daran, dass sich verschachtelte Suchprozesse nacheinander verbinden und niemand darüber nachdenken kann, wie dies anders gemacht werden kann, ohne die akzeptable Effizienz zu verlieren, obwohl sie es versucht haben. Natürlich werden eines Tages alle Lösungen gefunden, aber mit der falschen Reihenfolge werden sie so unrealistisch lange gesucht, dass dies keinen praktischen Sinn hat.

Es gibt Techniken zum Schreiben von Programmen, um dieses Problem zu vermeiden. Viele von ihnen erfordern jedoch besondere Fähigkeiten und Vorstellungskraft, und das Ergebnis sind sehr große Programme. Ein Beispiel ist der Begriff Größenbegrenzungstechnik und die Definition der binären Division mit Rest durch Multiplikation mit ihrer Hilfe. Anstatt dumm eine mathematische Definition zu schreiben

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm)) 

Ich muss eine rekursive Definition von 20 Zeilen + eine große Hilfsfunktion schreiben, deren Lesen unrealistisch ist (ich verstehe immer noch nicht, was dort getan wird). Es ist in Will Birds Dissertation im Abschnitt Pure Binary Arithmetic zu finden.

In Anbetracht des Vorstehenden möchte ich eine Art Suchmodifikation entwickeln, damit auch einfache und natürlich geschriebene Programme funktionieren.

Optimieren

Wir haben festgestellt, dass die Suche nicht beendet wird, wenn alles schlecht ist, es sei denn, Sie geben explizit die Anzahl der Antworten an und brechen sie ab. Deshalb haben sie beschlossen, genau mit der Unvollständigkeit der Suche zu kämpfen - es ist viel einfacher zu konkretisieren als „es funktioniert lange“. Im Allgemeinen möchte ich natürlich nur die Suche beschleunigen, aber die Formalisierung ist viel schwieriger, daher haben wir mit einer weniger ehrgeizigen Aufgabe begonnen.

In den meisten Fällen tritt bei divergierenden Suchvorgängen eine Situation auf, die leicht zu verfolgen ist. Wenn eine Funktion rekursiv aufgerufen wird und bei einem rekursiven Aufruf die Argumente gleich oder weniger spezifisch sind, wird beim rekursiven Aufruf erneut eine solche Unteraufgabe generiert und es tritt eine unendliche Rekursion auf. Formal klingt es so: Es gibt eine Substitution, bei der auf die neuen Argumente die alten angewendet werden. In der folgenden Abbildung ist ein rekursiver Aufruf beispielsweise eine Verallgemeinerung des Originals: Sie können ihn ersetzen $$$c_2$= [x, 3], $$$d_2$= x und erhalte den ursprünglichen Aufruf.



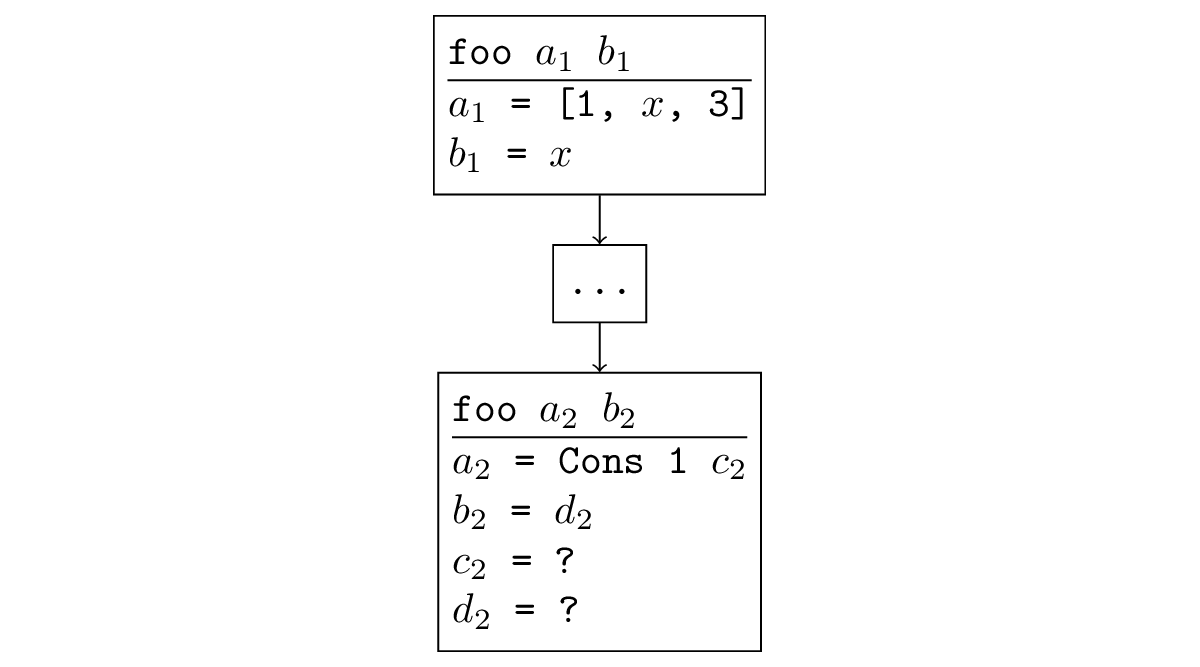
Es kann festgestellt werden, dass diese Situation auch in den Divergenzbeispielen auftritt, die wir bereits getroffen haben. Wie ich bereits geschrieben habe, wird beim Ausführen von Appendo in die entgegengesetzte Richtung ein rekursiver Aufruf mit freien Variablen anstelle aller Variablen ausgeführt, was natürlich weniger spezifisch ist als der ursprüngliche Aufruf, in dem das dritte Argument festgelegt wurde.

Wenn wir mit x =? und xr = [1, 2, 3] ist ersichtlich, dass der erste rekursive Aufruf erneut mit zwei freien Variablen erfolgt, so dass offensichtlich wieder neue Argumente auf die vorherigen übertragen werden können.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *) 

Anhand dieses Kriteriums können wir Abweichungen im Prozess der Programmausführung erkennen, verstehen, dass bei dieser Reihenfolge alles schlecht ist, und sie dynamisch in eine andere ändern. Dadurch wird im Idealfall für jeden Anruf genau die richtige Reihenfolge ausgewählt.
Sie können es naiv tun: Wenn im Konjunkt Divergenz festgestellt wird, hämmern wir alle Antworten ein, die er bereits gefunden hat, und verschieben die Ausführung auf später, wobei wir den nächsten Konjunkt „überspringen“. Wenn wir es dann weiter ausführen, sind möglicherweise bereits mehr Informationen bekannt, und es treten keine Abweichungen auf. In unseren Beispielen führt dies zu den gewünschten Swap-Konjunktionen.

Es gibt weniger naive Möglichkeiten, um beispielsweise die bereits geleistete Arbeit nicht zu verlieren und die Leistung zu verschieben. Bereits mit der dümmsten Variante der Änderung der Reihenfolge ist die Divergenz in allen einfachen Beispielen verschwunden, die unter der Nichtkommutativität der Konjunktion leiden, die wir kennen, einschließlich:

• Sortieren der Liste der Zahlen (es ist auch die Erzeugung aller Permutationen der Liste),
  
• Peano-Arithmetik und binäre Arithmetik,
  
• Erzeugung von Binärbäumen einer bestimmten Größe.
  

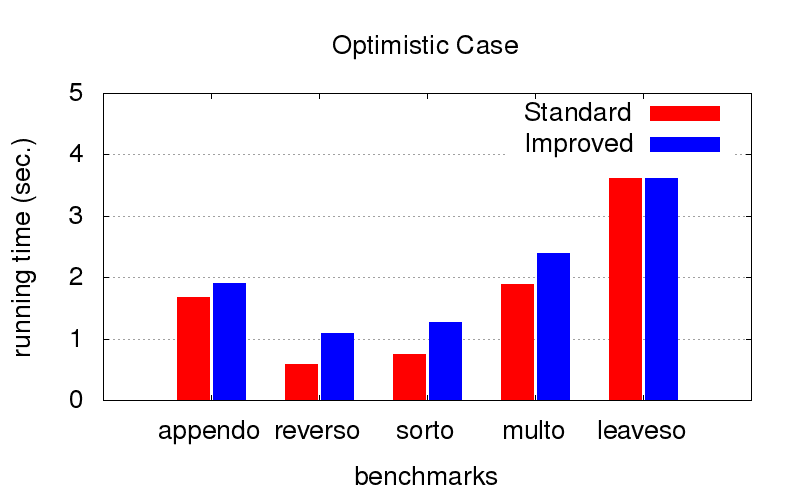
Dies war eine unerwartete Überraschung für uns. Neben der Divergenz kämpft die Optimierung auch gegen Programmverlangsamungen. Die folgenden Diagramme zeigen die Ausführungszeit von Programmen mit zwei unterschiedlichen Ordnungen in Konjunktionen (relativ gesehen eine der besten und eine von vielen schlechten). Es wurde auf einem Computer mit der Konfiguration von Intel Core i7 CPU M 620, 2,67 GHz x 4, 8 GB RAM mit dem Betriebssystem Ubuntu 16.04 gestartet.

Wenn die Reihenfolge bereits optimal ist (wir wählen sie von Hand aus), verlangsamt die Optimierung die Ausführung ein wenig, ist jedoch nicht kritisch


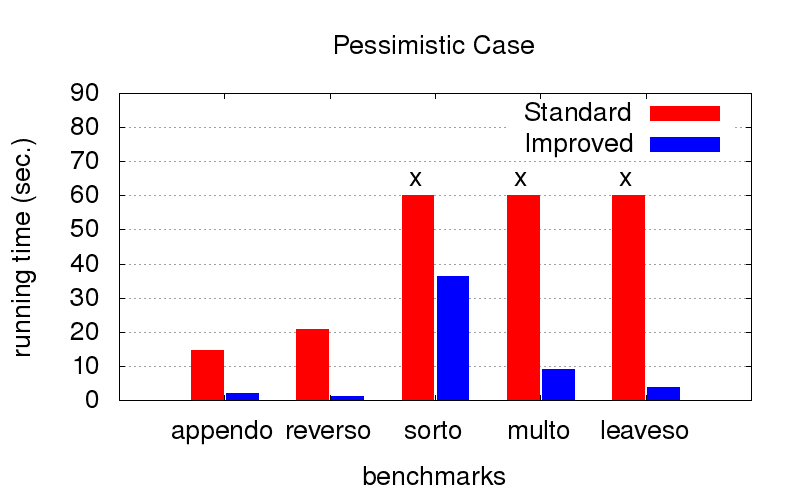
Wenn die Reihenfolge jedoch nicht optimal ist (z. B. nur zum Starten in die entgegengesetzte Richtung geeignet), wird sie bei der Optimierung viel schneller ausgeführt. Die Kreuze bedeuten, dass wir einfach nicht auf das Ende warten konnten, es funktioniert viel länger

Wie man nichts kaputt macht

All dies beruhte ausschließlich auf Intuition und wir wollten es streng beweisen. Theorie doch.

Um etwas zu beweisen, brauchen wir eine formale Semantik der Sprache. Wir haben die operative Semantik für miniKanren beschrieben. Dies ist eine vereinfachte und mathematisierte Version einer realen Sprachimplementierung. Es wird eine sehr eingeschränkte (daher einfach zu verwendende) Version verwendet, in der Sie nur die endgültige Ausführung von Programmen angeben können (die Suche sollte endgültig sein). Für unsere Zwecke ist dies genau das, was benötigt wird.

Um das Kriterium zu beweisen, wird zunächst das Lemma formuliert: Die Programmausführung aus einem allgemeineren Zustand wird länger funktionieren. Formal: Der Ausgabebaum in der Semantik hat eine große Höhe. Dies wird durch Induktion bewiesen, aber die Aussage muss sehr sorgfältig verallgemeinert werden, sonst ist die induktive Hypothese nicht stark genug. Aus diesem Lemma folgt, dass der Ausgabebaum einen eigenen Teilbaum mit größerer oder gleicher Höhe hat, wenn ein Kriterium während der Programmausführung funktioniert hat. Dies ergibt einen Widerspruch, da für eine induktiv gegebene Semantik alle Bäume endlich sind. Dies bedeutet, dass in unserer Semantik die Ausführung dieses Programms unaussprechlich ist, was bedeutet, dass die Suche darin nicht endet.

Die vorgeschlagene Methode ist konservativ: Wir ändern etwas nur, wenn wir davon überzeugt sind, dass alles bereits völlig schlecht und unmöglich schlechter zu machen ist, und brechen daher nichts in Bezug auf den Programmabschluss.

Der Hauptbeweis enthält viele Details, daher wollten wir ihn formell überprüfen, indem wir an Coq schreiben. Es stellte sich jedoch als technisch ziemlich schwierig heraus, so dass wir unsere Begeisterung abkühlten und uns ernsthaft mit der automatischen Überprüfung nur in der Magistratur befassten.

Posting

In der Mitte der Arbeit präsentierten wir diese Studie auf der Postersitzung des ICFP-2017 beim Studentenforschungswettbewerb . Dort haben wir uns mit den Machern der Sprache getroffen - Will Bird und Daniel Friedman - und sie sagten, dass es sinnvoll ist und wir es uns genauer ansehen müssen. Will ist übrigens generell mit unserem Labor bei JetBrains Research befreundet. Alle unsere Forschungen zu miniKanren begannen, als Will 2015 in St. Petersburg eine Sommerschule für relationale Programmierung abhielt.

Ein Jahr später brachten wir unsere Arbeit in eine mehr oder weniger vollständige Form und präsentierten den Artikel in den Grundsätzen und der Praxis der deklarativen Programmierung 2018.

Was mache ich in der Graduiertenschule?

Wir wollten uns weiterhin mit formaler Semantik für miniKanren und dem strengen Nachweis aller seiner Eigenschaften befassen. In der Literatur werden Eigenschaften (oft alles andere als offensichtlich) einfach postuliert und anhand von Beispielen demonstriert, aber niemand beweist etwas. Zum Beispiel ist das Hauptbuch über relationale Programmierung eine Liste von Fragen und Antworten, von denen jede einem bestimmten Code gewidmet ist. Selbst für die Vollständigkeit der Interleaving-Suche (und dies ist einer der wichtigsten Vorteile von miniKanren gegenüber Standard-Prolog) ist es unmöglich, einen strengen Wortlaut zu finden. Du kannst nicht so leben, beschlossen wir, und nachdem wir einen Segen von Will erhalten hatten, machten wir uns an die Arbeit.

Ich möchte Sie daran erinnern, dass die Semantik, die wir in der vorherigen Phase entwickelt haben, eine erhebliche Einschränkung aufwies: Es wurden nur Programme mit endlicher Suche beschrieben. In miniKanren sind laufende Programme auch deshalb interessant, weil sie unendlich viele Antworten auflisten können. Deshalb brauchten wir mehr coole Semantik.

Es gibt viele verschiedene Standardmethoden, um die Semantik einer Programmiersprache zu definieren. Wir mussten nur eine davon auswählen und an einen bestimmten Fall anpassen. Wir haben die Semantik als ein gekennzeichnetes Übergangssystem beschrieben - eine Reihe möglicher Zustände im Suchprozess und Übergänge zwischen diesen Zuständen, von denen einige markiert sind, was bedeutet, dass in dieser Phase der Suche eine andere Antwort gefunden wurde. Die Ausführung eines bestimmten Programms wird somit durch die Reihenfolge solcher Übergänge bestimmt. Diese Sequenzen können endlich (in einen Endzustand) oder endlos sein und gleichzeitig das Beenden und Nichtabschließen von Programmen beschreiben. Um ein solches Objekt mathematisch vollständig zu spezifizieren, muss eine koinduktive Definition verwendet werden.

— . , (, , — ..). , miniKanren' ( ).

, , — . . ( ), , .
( ): , , , .

, , / .

Coq'a. , , «. Qed». .