😈 📛 🥌 Wolfensteiny 3D - Reverse Engineering 251 Bytes JavaScript 🎖️ 🌶️ 🏉

Beim Schreiben von Code denken viele an nichts anderes als an die Logik des Programms selbst. Weniger Menschen denken darüber nach, den Code im Laufe der Zeit aus dem Speicher heraus zu optimieren. Aber nur wenige erreichen die letzte Stufe - das Programm wird auf eine kleine Rekordgröße komprimiert.

Schauen Sie sich zum Beispiel das Ergebnis von nur 251 Byte JavaScript an:

Nun, lassen Sie uns herausfinden, wie es funktioniert!

Woher kommt es?

Dieser Code sowie vieles, worauf ich in diesem Artikel eingegangen bin, befinden sich auf der Website p01.org des großartigen Mathieu 'p01' Henri, einem JavaScript-Entwickler, der nicht nur häufig daran beteiligt ist, den Code auf unmögliche Größen zu komprimieren. Das Quellmaterial dieses Artikels finden Sie hier .

Also, bevor Sie die 251 Bytes des Quellcodes sind.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

Es ist klar, dass nichts klar ist.

Den Code lesbar machen

Zunächst habe ich den gesamten JavaScript-Code der Einfachheit halber in einem separaten Tag ausgegeben.

Es ist ersichtlich, dass die Variablen E , h , Q , F und andere Konstanten sind, die durch ihre Werte / Objekte selbst ersetzt werden können, sowie die Namen ändern können.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

Hier wurde der Code aus der Zeichenfolge bereits in die Funktion übernommen, und die Zeichenfolge selbst bleibt unberührt. Wir werden ihn in Zukunft benötigen.

Konvertieren Sie nun die beiden äußeren Schleifen in while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

Wie sehen wir das?

Lassen Sie uns verstehen, warum wir es überhaupt sehen. Wenn Sie sich das Bild noch einmal ansehen, können Sie viel verstehen.

Klickbares Bild

Folgendes sehen wir:

Je weiter das Motiv entfernt ist, desto dunkler ist es
Der schräge Teil der angetroffenen Hindernisse ist unterschiedlich mit Linien und nicht mit Punkten überflutet.

Im Code wird die Zeichnung folgendermaßen wiedergegeben:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

Warum sehen wir in dieser Flut schwarzer Punkte volumetrische Objekte? Schließlich müssen wir uns nur mit verschiedenen Schwarztönen zufrieden geben - der Größe der schwarzen Punkte (wir können die Farbe nicht ändern, E.fillStyle ist zu lang!). Tatsächlich funktioniert es einfach, weil in einem zweidimensionalen Bild unser Auge hauptsächlich auf den Schatten und die Helligkeit des Lichts angewiesen ist.

Stellen Sie sich vor, Sie gehen mit nur einer Taschenlampe in den Händen einen dunklen Korridor entlang. Sie leuchten vor sich und sehen, dass einige Objekte näher und heller sind (eine Taschenlampe leuchtet, ein Hindernis ist hell, es gibt keine Schatten), während andere weiter und dunkler sind (Licht ist gestreut, schwach und wir sehen Dunkelheit - und wir spüren die Entfernung). Also hier - je weiter das Objekt (größer D ), desto größer wird ein schwarzes Quadrat auf dem Bildschirm.
Aber woher wissen wir, was hell sein muss und was nicht?

Zähle das Pixel

Nun beschäftigen wir uns mit diesem Monster:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

Also. All dieser Ausdruck ist ein Raymarching-Algorithmus mit festem Schritt , mit dem Sie den Schnittpunkt des Strahls mit den Blöcken finden können. Für jedes Pixel des Bildschirms starten wir einen Strahl und folgen ihm mit einem festen Schritt von 0.1 . Sobald wir auf ein Hindernis stoßen, beenden wir den Algorithmus und zeichnen ein Pixel auf den Bildschirm, wobei wir den Abstand zum Hindernis kennen.

Beginnen wir mit dem Lesen dieses Codes in Teilen.

Bedingung D * y / size - D / 2 | 0 D * y / size - D / 2 | 0 kann dargestellt werden als

ö ß ö ß ö ß

$D * (\ frac {y} {Größe} - \ frac {1} {2}) = D * (\ frac {y - Größe / 2} {Größe}) <1$ Dann zeigt der Ausdruck in Klammern die „Abweichung“ y von der Bildschirmmitte (in Bruchteilen des Bildschirms). Wir versuchen also zu verstehen, ob sich der Balken zwischen Boden und Decke befindet oder nicht. Wenn wir also den Boden (oder die Decke) berühren, verlassen wir die Schleife weiter, um ein Pixel zu zeichnen und zu zeichnen.
Und wenn wir uns nicht berühren, setzen wir die Berechnungen fort: Wir suchen nach den aktuellen Koordinaten des Strahls.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

Warum cos (T - 8)?

Es stellt sich also heraus, dass

$cos (x-8) \ ca. sin (x)$ mit einer Genauigkeit von 0,15 Radiant. Alles weil

$\ frac {5 \ pi} {2} \ ca. 8,15 \ ca. 8$

und dann

$cos (\ alpha-8) \ ca. cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

Es lohnt sich darüber zu sprechen, wie ein Punkt im Raum im Allgemeinen auf einen Block überprüft wird. Die Karte selbst stammt aus dem Quellcode ( F ) und sieht folgendermaßen aus:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

Es sieht also wie in Bewegung aus, hier wird das Sichtfeld der Kamera angezeigt.

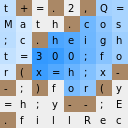
Die Zellen, deren Symbolcode kleiner als der Punktcode - "." Ist, sind dunkel markiert "." - das heißt, die Zeichen !"#$%&'()*+,-. Nun runden wir die Koordinaten des Strahls und versuchen herauszufinden, ob der Buchstabe im angegebenen" Koordinaten "-Index dunkel ist (Hindernis) oder nicht (den Strahl weiter fliegen).

Da der Index eins ist und die Koordinaten zwei sind, verwenden wir den Hack:

 var boxIndex = xcoord & 7 | ycoord << 3;

Als Ergebnis erhalten wir eine Nummer, die die Blocknummer widerspiegelt (gut oder Hohlräume).

Kehren wir zum Code zurück. Jetzt sieht er anständig aus.

Der Code ist etwas fett

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

Zurück zum Zeichnen

Warum brauchten wir das alles? Nachdem wir diesen Algorithmus ausgeführt haben, kennen wir die Entfernung zum Objekt und können sie zeichnen. Eine Frage blieb jedoch unbeantwortet: Wie kann die Decke von einer separaten Einheit unterschieden werden? Immerhin sind der Abstand zur Decke und zum Block Zahlen, die nicht anders sind! Tatsächlich haben wir diese Frage bereits beantwortet.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

Es gibt eine Bedingung im Code, die sich auf die Variable b bezieht und die Breite des "großen schwarzen Pixels" beeinflusst: b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . Lassen Sie uns diesen Zustand entfernen und sehen, was ohne ihn passiert:

Es gibt keine Grenzen zwischen den Blöcken und der Decke! (anklickbar)

Bedingung b - xcoord gibt uns eine konstante Breite, wenn die Koordinatenänderung 0 ist. Und wann kann dies nicht passieren? Dies geschieht nicht nur, wenn wir nicht zur (2) -Zeile im Code gelangen:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

Dies bedeutet, dass das Programm den Zyklus in Zeile (3) früher verlässt, wenn der Strahl in einer Richtung fast senkrecht zu seiner Wand in einen undurchsichtigen Block geht, dh in die "Fläche" des Blocks fällt. Somit unterscheiden sich alle Blöcke vom Boden und der Decke.

So entsteht dieses wunderschöne 3D-Bild, das nicht nur das Auge erfreut, sondern Sie auch darüber nachdenken lässt, wie und warum es funktioniert. Sie können diesen Code hier in Aktion sehen (off. Site des Entwicklers dieses Wunders).

Wolfensteiny 3D - Reverse Engineering 251 Bytes JavaScript

Den Code lesbar machen

Wie sehen wir das?

Zähle das Pixel

Zurück zum Zeichnen

More articles: