Unmögliche Pfanne und andere Penrose-Kacheln gewinnen

1974 schuf der britische Mathematiker Roger Penrose einen revolutionären Satz von Kacheln, mit denen eine unendliche Ebene mit einem sich nie wiederholenden Muster gefüllt werden kann. 1982 entdeckte der israelische Kristallograph Daniel Shekhtman eine Metalllegierung, deren Atome in einer Reihenfolge angeordnet waren, wie sie in der Materialwissenschaft noch nie zuvor vorgekommen war. Penrose erreichte eine massive öffentliche Anerkennung, die Mathematikern selten zuteil wurde. Shekhtman erhielt den Nobelpreis. Beide Wissenschaftler stellten die menschliche Intuition in Frage und veränderten die Grundlagen des Verständnisses der Struktur der Natur. Sie stellten fest, dass unendliche Variabilität auch in einer hochgeordneten Umgebung auftreten kann.

Im Zentrum ihrer Entdeckungen steht eine „verbotene Symmetrie“, die so genannt wird, weil sie der tief verwurzelten Verbindung zwischen Symmetrie und Wiederholbarkeit widerspricht. Die Symmetrie basiert auf den Reflexionsachsen - alles, was sich auf einer Seite der Linie befindet, wird auf der anderen Seite dupliziert. In der Mathematik wird diese Verbindung durch Muster des Kachelraums ausgedrückt. Symmetrische Formen wie Rechtecke und Dreiecke können die Ebene ohne Lücken und Überlagerungen füllen und ein sich ständig wiederholendes Muster erzeugen. Wiederholte Muster werden als "periodisch" bezeichnet und sollen "Übertragungssymmetrie" aufweisen. Wenn Sie das Muster (Muster) von Ort zu Ort verschieben, sieht es gleich aus.

Als mutiger und ehrgeiziger Wissenschaftler interessierte sich Penrose mehr nicht für dieselben Muster und Wiederholbarkeit, sondern für unendliche Variabilität. Insbesondere interessierte er sich für „aperiodische“ Kacheln, dh für Zahlenreihen, die eine unendliche Ebene ohne Lücken und Überlagerungen füllen können, und das Kachelmuster wird nie wiederholt. Dies war eine schwierige Aufgabe, da er keine Figuren (Kacheln) mit zwei, drei, vier oder sechs Symmetrieachsen verwenden konnte - Rechtecke, Dreiecke, Quadrate oder Sechsecke -, weil sie auf einer unendlichen Ebene periodische oder sich wiederholende Muster erzeugen würden. Das heißt, er musste Figuren verwenden, von denen angenommen wurde, dass sie beim Füllen des Flugzeugs Lücken hinterlassen - Figuren, die Symmetrie verboten haben.

Um seine eigene Ebene nicht wiederholter Muster zu erzeugen, wandte sich Penrose der fünfachsigen Symmetrie zu - Pentagonen, insbesondere, weil es seiner Meinung nach „einfach schön ist, Pentagone zu betrachten“. Das Bemerkenswerte an Penrose 'Figuren war, dass diese Figuren zwar aus den Linien und Ecken der Rechtecke stammten, aber keine hässlichen Lücken hinterließen. Sie passen eng aneinander, biegen und drehen sich im Flugzeug, sind immer nahe an der Wiederholbarkeit, erreichen es aber nie.

Das Mosaik von Penrose hat aus zwei Hauptgründen die Aufmerksamkeit der Öffentlichkeit auf sich gezogen. Zunächst fand er einen Weg, aus nur zwei Arten von Formen unendlich wechselnde Muster zu erzeugen. Zweitens waren seine Fliesen einfache, symmetrische Figuren, die an sich keine Anzeichen ungewöhnlicher Eigenschaften zeigten.


Penrose schuf verschiedene Varianten seiner aperiodischen Figurenreihen. Eine der bekanntesten heißt "Schlange" und "Pfeil". Der „Drachen“ sieht aus wie ein Kinderdrachen, und der „Pfeil“ sieht aus wie ein vereinfachter Umriss eines Stealth-Bombers. Beide sind entlang der Symmetrieachsen klar unterteilt und haben jeweils einfache symmetrische Bögen auf der Oberfläche. Penrose definierte eine Regel für das Platzieren von Formen: Für das "richtige" Platzieren von Kacheln müssen diese Bögen übereinstimmen, wodurch untrennbare Kurven entstehen. Ohne diese Regel können „Schlangen“ und „Pfeile“ in sich wiederholenden Mustern angeordnet werden. Wenn Sie diese Regel befolgen, kommt es nie zu Wiederholungen. "Schlange" und "Pfeil" füllen das Flugzeug unendlich, tanzen um ihre fünf Achsen und erzeugen Sterne und Zehnecke, geschwungene Kurven, Schmetterlinge und Blumen. Die Figuren werden wiederholt, aber neue Variationen erscheinen in ihnen.

Einen klinischen Vergleich bietet der klinische Professor für Mathematik Edmund Harriss von der University of Arkansas, der über Penrose-Fliesen promoviert hat. „Stellen Sie sich vor, Sie leben in einer Welt voller Quadrate. Du fängst an zu laufen, und wenn du am Ende des Platzes angekommen bist, ist der nächste genau der gleiche und du weißt, was du sehen wirst, wenn du dich endlos weiter bewegst. " Penrose Fliesen haben genau das Gegenteil. „Unabhängig davon, welche Informationen Sie haben, welchen Teil des Musters Sie auch sehen, Sie können niemals vorhersagen, was als nächstes passieren wird. Es wird immer etwas geben, das du noch nie gesehen hast. “

Einer der merkwürdigen Aspekte der aperiodischen Aufteilung einer Ebene besteht darin, dass Positionsinformationen auf irgendeine Weise über große Entfernungen übertragen werden. Die an einer Stelle verlegte Penrose-Kachel verhindert die Platzierung anderer Kacheln in Hunderten (und auch Tausenden und Millionen) Kacheln. "Eine lokale Einschränkung schafft irgendwie eine globale Einschränkung", sagt Harriss. "Dies deutet darauf hin, dass diese Kacheln in keinem Maßstab periodisch etwas erzeugen." Möglicherweise haben Sie die Wahl, beispielsweise eine „Schlange“ in einem Bereich oder einen „Pfeil“ an einem entfernten Ort zu platzieren. Alle Kacheln reichen aus, aber nicht beide.


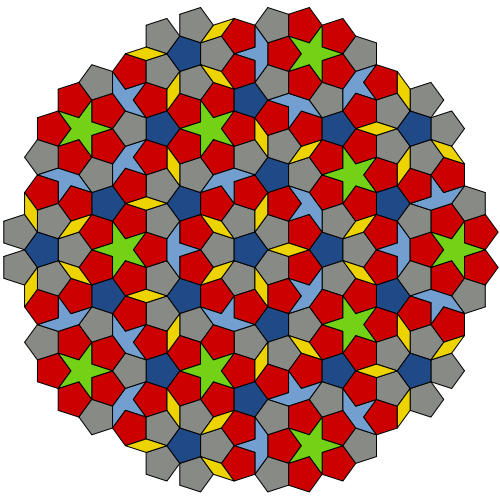
Diese Kacheln, die ein endloses, sich nicht wiederholendes Muster bilden, drücken das Fibonacci-Verhältnis aus, das auch als "goldener Schnitt" bekannt ist. Zwei Zahlen haben einen goldenen Schnitt, wenn das Verhältnis einer kleineren zu einer größeren Zahl dem Verhältnis einer größeren Zahl zur Summe zweier Zahlen entspricht. In diesem Fall ist das Verhältnis der Fläche der "Schlange" zur Fläche des "Pfeils" der goldene Schnitt. Das Verhältnis der langen Seite der "Schlange" zu ihrer kurzen Seite ist auch der goldene Schnitt.

Penrose-Fliesen können auch in kleinere Versionen von sich selbst unterteilt werden. Eine "Schlange" besteht aus zwei kleineren "Schlangen" und zwei Hälften eines "Pfeils". Der "Pfeil" besteht aus einer kleineren "Schlange" und zwei "Pfeil" Teppichen. (Bei jeder korrekten Kachelung von Penrose sind diese Hälften der „Pfeile“ miteinander ausgerichtet. Aus mathematischer Sicht können sie als ganze „Pfeile“ betrachtet werden.) „Angenommen, wir haben ein Stück des Penrose-Mosaiks, das aus A- „ Schlangen “und B- „ Pfeilen “besteht. "" Sagt Harriss. "Wenn ich sie unterteile, bekomme ich 2 A + B " Schlangen "und A + B " Pfeile ".

Wenn Sie diese Ersetzung unendlich oft durchführen, können Sie den Gesamtanteil jedes Kacheltyps so berechnen, als ob er auf einer unendlichen Ebene angeordnet wäre. Bei solchen Berechnungen führt ein sich wiederholendes Muster immer zu einer rationalen Zahl. Wenn der Anteil eine irrationale Zahl ist, bedeutet dies, dass sich das Muster niemals vollständig wiederholt. Bei den Berechnungen für Penrose-Kacheln wird nicht nur die irrationale Zahl erhalten, sondern auch das Fibonacci-Verhältnis. Das Verhältnis von „Pfeilen“ zu „Schlangen“ entspricht dem Verhältnis von „Schlangen“ zur Gesamtzahl der Kacheln.

Angesichts der Tatsache, dass der Fibonacci-Anteil in der Natur allgegenwärtig ist - von Ananas bis zu Kaninchenpopulationen - ist es noch seltsamer, dass dieser Anteil für das Kachelsystem von grundlegender Bedeutung ist, was anscheinend nichts mit der physischen Welt zu tun hat. Penrose schuf etwas Neues in der Wissenschaft und faszinierte genau dort, dass es nicht so funktionieren sollte wie die Natur. Es war, als hätte Penrose eine Science-Fiction-Geschichte über eine neue Tierart geschrieben, und dann entdeckte der Zoologe diese auf der Erde lebende Art. In der Tat sind Penrose-Kacheln mit dem Goldenen Schnitt, der von uns erfundenen Mathematik und der Mathematik der Welt um uns herum verbunden.


Penrose nahm das Studium der verbotenen Symmetrie auf und konnte nicht ahnen, dass er Teil des Denkwandels geworden war, der zur Entdeckung eines neuen Feldes der Mathematik führte. Schließlich ist Symmetrie sowohl für die reine Mathematik als auch für die natürliche Welt von grundlegender Bedeutung. Der Astrophysiker Mario Livio bezeichnete die Symmetrie als "eines der notwendigsten Werkzeuge zur Entschlüsselung der Naturstruktur". Die Natur verwendet Quadrate und Sechsecke aus demselben Grund wie der Mensch: Sie sind einfach, effizient und geordnet. Wenn Pentagone selbst für eine so einfache Aufgabe wie das Füllen von Bodenfliesen in der Innenarchitektur unpraktisch erschienen, wurde natürlich angenommen, dass sie nicht zur Erzeugung von Atomen in festen Materialien wie Kristallen verwendet werden könnten.

Kristalle bestehen aus dreidimensionalen Atomgittern. Kristalle wachsen durch Hinzufügen neuer Atome und Erweitern der Gitter. Dies geschieht am effizientesten, wenn sich Atome in sich wiederholenden Mustern aneinanderreihen. Dort endete jahrzehntelang die Geschichte: Kristalle wiederholten Strukturen. Der Punkt.

Aber dann, 1982, ging Shekhtman von der Technion University in Haifa in den Kreativurlaub und begann beim National Bureau of Standards zu arbeiten. Er fummelte in einem Labor aus Aluminium-Mangan-Legierung herum. Die durch seine kristallinen Strukturen erzeugten Beugungsmuster schienen keiner der den Kristallographen bekannten Standardsymmetrien zu ähneln. Tatsächlich reihten sich die Atome in den Pentagonen, Rauten, „Schlangen“ und „Pfeilen“ an, die Penrose in der Welt der Mathematik entdeckt hatte.

„Natürlich war ich mit Penrose-Fliesen vertraut“, sagt Schechtman. Aber er hatte keinen Grund, ihre Verbindung mit dieser Legierung zu vermuten. „Ich habe nicht verstanden, was es ist. In den nächsten Monaten wiederholte ich meine Experimente immer wieder. Am Ende meines kreativen Urlaubs wusste ich genau, was es nicht war, aber ich hatte immer noch keine Ahnung, was es war. “

Um zu verstehen, was er entdeckte, musste Schechtman wie Penrose seine üblichen intuitiven Ideen hinterfragen. Er musste die verbotene Symmetrie und ihre fünfeckige Verwirrung mit mangelnder Wiederholbarkeit akzeptieren. Während seines Aufenthalts in Israel wollte er nur ungern erkennen, dass er eine sich nicht wiederholende kristalline Atomstruktur entdeckt hatte. Niemand in der Welt der Materialwissenschaften konnte diese Entdeckung jedoch zunächst Kristallen zuschreiben. Daher wurden sie "Quasikristalle" genannt.

Penrose 'bizarre Mathematik schien in die natürliche Welt ausgebrochen zu sein. „Seit 80 Jahren werden Kristalle als„ geordnete und periodische “Strukturen definiert, da alle Kristalle, die wir seit 1912 untersucht haben, periodisch waren“, erklärt Schechtman. „Erst 1992 organisierte die International Union of Crystallographers ein Komitee, um eine neue Definition für das Wort Kristall auszuwählen. Diese neue Definition ist ein Paradigmenwechsel für die Kristallographie. “

Es war nicht nur die einfache Trägheit des Denkens, die Shekhtmans Verständnis und Akzeptanz der Entdeckung verhinderte. Aperiodische kristalline Strukturen waren nicht nur unbekannt - sie wurden als unnatürlich angesehen. Denken Sie daran, dass die Position einer Penrose-Kachel die Formen in Tausenden von Kacheln beeinflussen kann - lokale Einschränkungen schaffen globale. Wenn jedoch ein Kristall Atom für Atom gebildet wird, sollte es kein Naturgesetz geben, das die Beschränkungen schafft, die Penrose-Fliesen innewohnen.

Es stellte sich heraus, dass Kristalle nicht immer Atom für Atom bilden. „In sehr komplexen intermetallischen Verbindungen sind die Elemente riesig. Sie sind nicht lokal “, sagt Schechtman. Wenn gleichzeitig große Kristallfragmente gebildet werden und nicht durch allmähliches Wachstum von Atomen, können Atome, die sehr weit voneinander entfernt sind, die gegenseitige Position beeinflussen, genau wie bei Penrose-Kacheln.

Wie bei vielen Tabus wurde die verbotene Symmetrie als eine der akzeptablen Existenzformen in der Natur anerkannt. Quasikristalle wurden nicht nur Gegenstand von Studien auf einem neuen Gebiet der wissenschaftlichen Forschung: Es stellte sich heraus, dass sie viele nützliche Eigenschaften haben, die sich aufgrund ihrer ungewöhnlichen Struktur ergeben. Zum Beispiel liefert ihre asymmetrische Konfiguration von Atomen ihnen eine niedrige Oberflächenenergie, das heißt, wenig kann an ihnen haften bleiben. So wurden quasikristalline Beschichtungen in antihaftbeschichteten Küchenutensilien verwendet. (Als Penrose seine neuen Fliesen herstellte, konnte er sich nicht vorstellen, dass sie in der Kristallographie verwendet werden würden, ganz zu schweigen vom Braten von Eiern.) Darüber hinaus weisen Quasikristalle normalerweise eine geringe Reibung und Abnutzung auf, sodass sie ideale Beschichtungen für Rasierer und chirurgische Eingriffe sind Instrumente oder andere scharfe Instrumente, die sich auf den menschlichen Körper beziehen.


Da sich Quasikristallstrukturen niemals wiederholen, erzeugen sie einzigartige Beugungsmuster elektromagnetischer Strahlung. Photonikforscher interessieren sich dafür, wie sie Lichtdurchlässigkeit, Reflexionsvermögen und Photolumineszenz beeinflussen. Wenn sie gekühlt werden, fällt ihr elektrischer Widerstand auf nahezu Null ab. Sie absorbieren aber auch Infrarotstrahlung und erwärmen sich daher sehr schnell auf hohe Temperaturen. Aus diesem Grund erweisen sie sich als sehr nützliche Ergänzung zu 3D-Druckern, bei denen Kunststoffpulver als Ausgangsmaterial verwendet wird. Shekhtman erklärt: Wenn ein quasiperiodisches Pulver damit gemischt und Infrarotstrahlung ausgesetzt wird, erwärmt sich das quasiperiodische Pulver „extrem schnell und schmilzt die umgebenden Kunststoffpartikel, wodurch sie zusammenkleben“.

Niemand weiß, wie die Geschichte der verbotenen Symmetrie endet. Mathematiker erforschen weiterhin die Eigenschaften von Penrose-Fliesen. Quasikristalle bleiben sowohl in der Grundlagenforschung als auch in der angewandten Forschung Gegenstand des Studiums. Aber bisher war diese Reise unglaublich. In den letzten 40 Jahren hat sich die fünfachsige Symmetrie von unpraktisch zu wertvoll, von unnatürlich zu völlig natürlich, von verboten zu dominant gewandelt. Und für diese Transformation müssen wir uns bei zwei Wissenschaftlern bedanken, die ihre üblichen Ideen aufgegeben haben, um eine bemerkenswerte neue Form endloser Variationen in der Natur zu entdecken.

Über den Autor: Patchen Bars ist eine in Toronto ansässige Journalistin und Autorin. Derzeit arbeitet er an einem Buch über die Beziehung zwischen reiner Mathematik und der natürlichen Welt.