Fraktale in irrationalen Zahlen

Dieser Artikel ist eine Fortsetzung meines ersten Artikels , Fraktale in Primzahlen .

Nächster Artikel: Fraktale in irrationalen Zahlen. Teil 2



In einem früheren Artikel haben wir gelernt, wie man selbstähnliche Muster unter Verwendung von Primzahlen zeichnet. In diesem Artikel werde ich die fraktale Natur der Zahl zeigen $$$\ sqrt {2}$ .
Ohne Vorwort. Unter Katze.

Wir werden Terminologie und Notation definieren. In der Mathematik werden die nachfolgend beschriebenen Systeme als Billard bezeichnet . Weiter werden wir diesen Begriff verwenden. Die Abmessungen des rechteckigen Billards werden mit bezeichnet $$$M$ (Breite) und $$$N$ (Höhe).

Binäres Billard

Im vorherigen Artikel haben wir ein rechteckiges Billard mit Seiten genommen $$$M$ und $$$N$ , warf einen Ball hinein und markierte die Flugbahn mit einer gestrichelten Linie durch die Zelle:



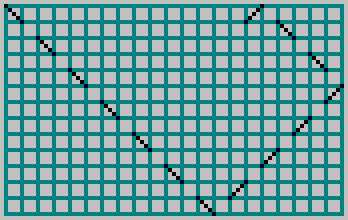
Für beide einfach $$$M$ und $$$N$ wir bekommen das Muster:



In der Binärversion markieren wir die Flugbahn nicht mit einer gestrichelten Linie, sondern malen die Zellen abwechselnd mit Schwarzweiß (wir bilden ein Binärarray, setzen 0 für Schwarz und 1 für Weiß in die entsprechende Zelle):



Grenzreflexionsregeln:



Für beide einfach $$$M$ und $$$N$ Die Flugbahn verläuft durch jede Zelle:




Wenn die Parteien einen gemeinsamen Teiler haben, betritt der Ball die Ecke, bevor er durch jede Zelle geht:



Es ist zweckmäßig, diesen Fall als Billard in einem Rechteck mit Seiten zu betrachten $$$\ frac {M} {GCD}$ und $$$\ frac {N} {GCD}$ (GCD ist der größte gemeinsame Faktor):



Bevor Sie fortfahren, füllen Sie die Tabelle aus, die der Benutzer Captain1312 in seinem Artikel vorgeschlagen hat (wir werden die Seiten des Billards in GCD unterteilen).

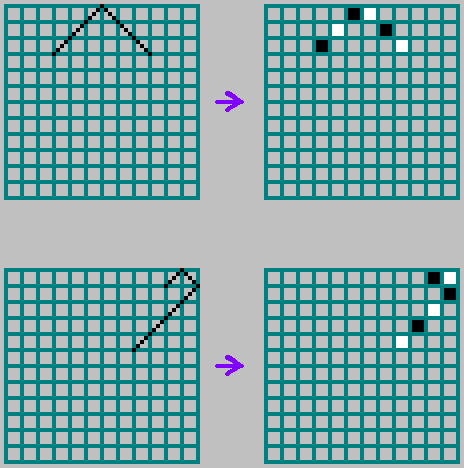
$$$(1, 0)$ ein bisschen

Für jeden Billardtisch $$$M$ und $$$N$ nimm ein bisschen mit Koordinaten $$$(1, 0)$ .



Wenn $$$M$ ist ein Teiler $$$N$ - dann ein bisschen mit Koordinaten $$$(1, 0)$ fehlt ( $$$\ frac {M} {GCD} = 1$ ) In diesem Fall nehmen wir das invertierte Bit mit den Koordinaten $$$(0, 1)$ .

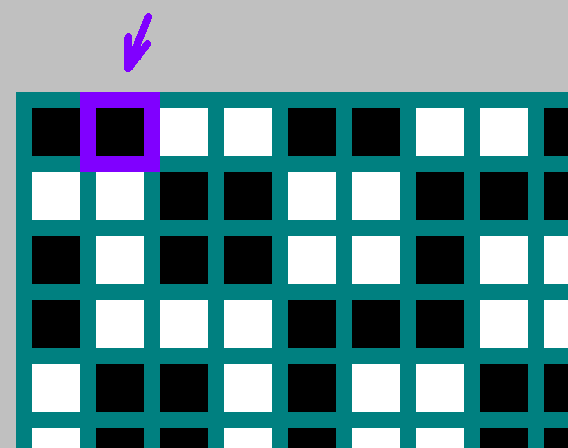
Füllen Sie die Tabelle aus. Der Ursprung ist die obere linke Ecke. Von $$$x$ - Breite des Billards $$$M$ von $$$y$ - Höhe $$$N$ . Für jedes Billard markieren wir ein bisschen $$$(1, 0)$ oder invertiertes Bit $$$(0, 1)$ (Wir werden unten auf dieses Thema zurückkommen).

Binäre Sequenz

Warum haben wir das Bit umgedreht, als die Breite des Billards $$$M = 1$ ? Für beide einfach $$$M$ und $$$N$ Die Flugbahn des Balls verläuft durch jede Zelle. Zwischen der oberen und linken Wand des Billards passiert der Ball jedes Mal eine gerade Anzahl von Zellen.





Die Bits in der linken Spalte sind die invertierten Bits aus der oberen Zeile. Wir nehmen nicht das Nullbit - die Flugbahn beginnt damit:



Außerdem können wir sicher jedes zweite Bit aus dieser Sequenz (Bit) werfen $$$2_ {n-1}$ - invertiertes Bit $$$2_ {n}$ ):



Habe die Sequenz $$$10 100 110 110$ für Billard $$$(21,13)$ . Die Sequenz ist für jeden einzigartig. $$$M$ und $$$N$ .

Egal wie hoch $$$N$ wir haben nicht genommen - der Ball geht immer entlang der Flugbahn $$$2N$ zwischen zwei Reflexionen von der oberen Wand. Von der oberen Wand aus beginnt die Bewegung immer mit einem „0“ -Bit (schwarze Zelle) und endet mit einem „1“ -Bit (weiße Zelle):



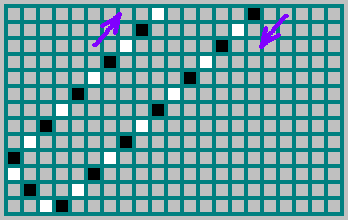
In der Tat die Sequenz (die wir oben hervorgehoben haben - $$$10 100 110 110$ ) zeigt an, auf welcher Seite der Ball eingeflogen ist: 1 - wenn der Ball eingeflogen ist, reflektiert von der rechten Wand und 0 - wenn der Ball eingeflogen ist, reflektiert von der linken Wand. Auf dem Bild ist die Flugbahn des Balls schwarz markiert, wenn sich der Ball nach rechts bewegt, und weiß, wenn er sich nach links bewegt:




Diese Sequenz ( $$$10 100 110 110$ ) enthält alle notwendigen Informationen zum Muster. Damit können wir das ursprüngliche Muster wiederherstellen (und sogar über den unteren Rand des Musters hinausblicken). Nimm ein Quadrat mit Seiten $$$M$ . Wir ordnen die Teile unserer Sequenz an den Stellen an, an denen der Ball die obere Wand berührt (der Abstand zwischen den benachbarten Berührungen des Balls beträgt 2 Zellen).



Wenn das entsprechende Bit = 1 ist, bewegen wir uns nach links und markieren die Flugbahn durch die Zelle. Wenn Bit = 0 - nach rechts bewegen.



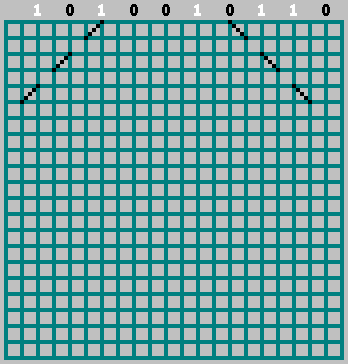
Vergessen Sie in diesem Fall nicht das Nullbit:



Gif:



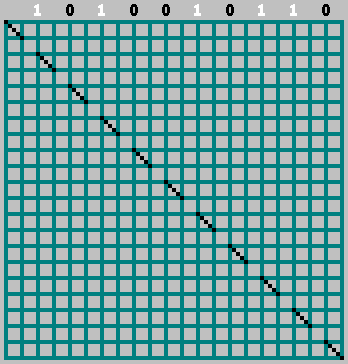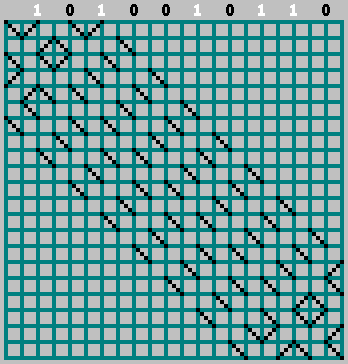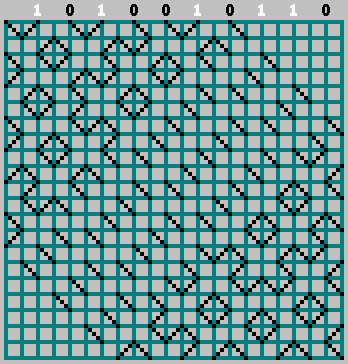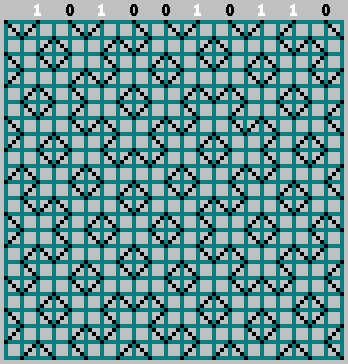
Wir haben das ursprüngliche Muster erhalten (und etwas über den unteren Rand hinausgeschaut):



Skript zur Visualisierung von Binärsequenzen

Wir können diese Sequenz mit dem Rest der Division erstellen.

Eindimensionales Billard

Auf der numerischen Achse $$$X$ nimm zwei Punkte: $$$0$ und $$$M$ .



Wenn Sie sich von einem Punkt zum anderen bewegen, messen Sie die Entfernung $$$N$ ::



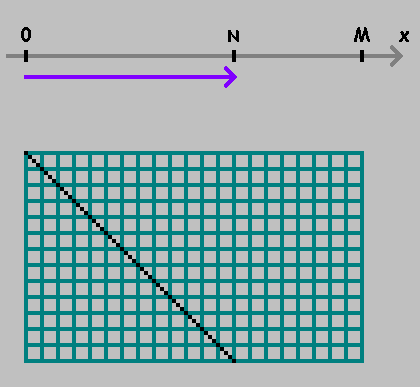
Markierte den Punkt. Wir messen weiterhin den Abstand von diesem Punkt und halten dabei die Richtung ein. Wenn Sie den Punkt erreicht haben $$$0$ oder $$$M$ - Richtung ändern:



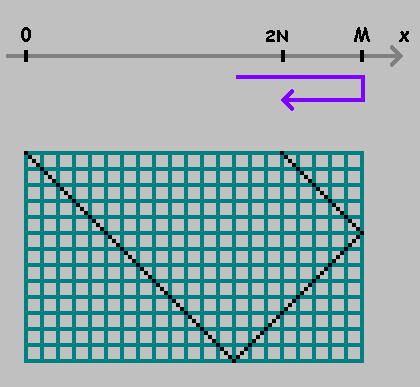
Wie in den obigen Abbildungen zu sehen ist, zeigt der erste Punkt die Stelle, an der der Ball die Bodenwand des Billards berührt. Dieser Punkt interessiert uns nicht. Wir werden nur Punkte fixieren $$$2kN$ für $$$k = 0,1,2, ...$ .

Wie markiere ich diese Punkte? Drehen Sie unser Billard um die Achse $$$X$ . Markieren Sie die Punkte $$$0, M, 2M, 3M, ...$ . Jetzt den Punkt erreichen $$$M$ Wir ändern nicht die Bewegungsrichtung, sondern bewegen uns weiter zum Punkt $$$2M$ .



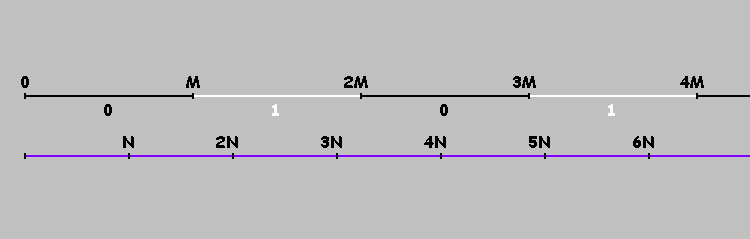
Vielfache $$$M$ Teilen Sie unsere Achse in Segmente. Wir markieren diese Segmente bedingt mit Einsen und Nullen (abwechselnd). Bei mit Nullen markierten Segmenten bewegt sich die Kugel (in einem rechteckigen Billard) von links nach rechts. Auf den mit Einheiten gekennzeichneten Segmenten - von rechts nach links. Oder einfacher: Der Ball bewegt sich von links nach rechts, wenn $$$Q_k = 0$ für

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

(Besondere Aufmerksamkeit sollte dieser Formel gewidmet werden. Als nächstes werden wir darauf zurückkommen.)

Es ist leicht zu erkennen, dass der Punkt, an dem der Ball die obere Wand des Billards berührte, der Rest der Division ist $$$2kN$ auf $$$M$ . In diesem Fall können wir die Bewegung des Balls nicht in die entgegengesetzte Richtung fixieren. Wir übernehmen den gesamten Teil der Division $$$2kN$ auf $$$M$ Wenn es gerade ist, betrachten wir den Rest der Teilung $$$2kN$ auf $$$M$ . Teilen Sie den resultierenden Rest durch 2 (der Abstand zwischen benachbarten Kontaktpunkten beträgt zwei Zellen). Erhielt die Indizes der Elemente des Arrays, die wir mit Nullen füllen müssen. Die restlichen Elemente sind mit Einheiten gefüllt (der Ball bewegt sich von der rechten Wand nach links).

Sequenzlänge = $$$\ frac {M} {2}$ .

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

Jetzt können wir eine binäre Sequenz für Billard mit beliebigen Seiten erstellen $$$M$ und $$$N$ (durch natürliche Zahlen).
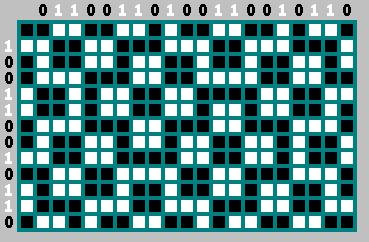
Einige Beispiele:
144 x 89 (Fibonacci-Zahlen):
010100101101001011010110100101101001010010110100101101011010010110100101

169 x 70 (Pell-Nummern):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55 (ungerade Fibonacci-Zahlen $$$F_n$ und $$$F_ {n-3}$ ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


Wir haben Sequenzen. Wie sonst können Sie Binärsequenzen visualisieren? Verwenden von Turtle-Grafiken .

Schildkrötengrafiken

Zeichne eine Linie. Als nächstes nehmen wir abwechselnd die Bits aus unserer Sequenz. Wenn bit = 1 - drehen Sie das Segment relativ zum vorherigen $$$60 ^ {\ circ}$ (im Uhrzeigersinn). Wenn bit = 0 - drehen Sie das Segment um $$$-60 ^ {\ circ}$ . Der Anfang des nächsten Segments ist das Ende des vorherigen.



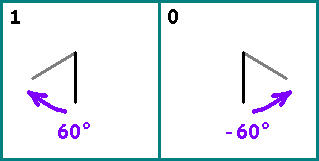
Nehmen Sie zwei ausreichend große Fibonacci-Zahlen: $$$F_ {29} = 514229$ und $$$F_ {28} = 317811$ .

Erstellte die Sequenz:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 Zeichen plus Nullbit).

Wir visualisieren mit Schildkrötengrafiken. Die Größe des Anfangssegments beträgt 10 Pixel (das Anfangssegment in der unteren rechten Ecke):



Die Größe des Anfangssegments beträgt 5 Pixel:



Die Größe des Anfangssegments beträgt 1 Pixel:



Das nächste Beispiel sind Pell-Zahlen.

$$

$$P_n = \ begin {Fälle} 0, n = 0; \\ 1, n = 1 \\ 2P_ {n-1} + P_ {n-2}, n> 1 \ end {Fälle}$$

Nimm $$$P_ {16} = 470832$ und $$$P_ {15} = 195025$ .

Sequenz:
0010100101011010100101011010100101001010110101001010110101000010101101 (235415 Zeichen plus Nullbit).

Die Größe des Anfangssegments beträgt 1 Pixel:



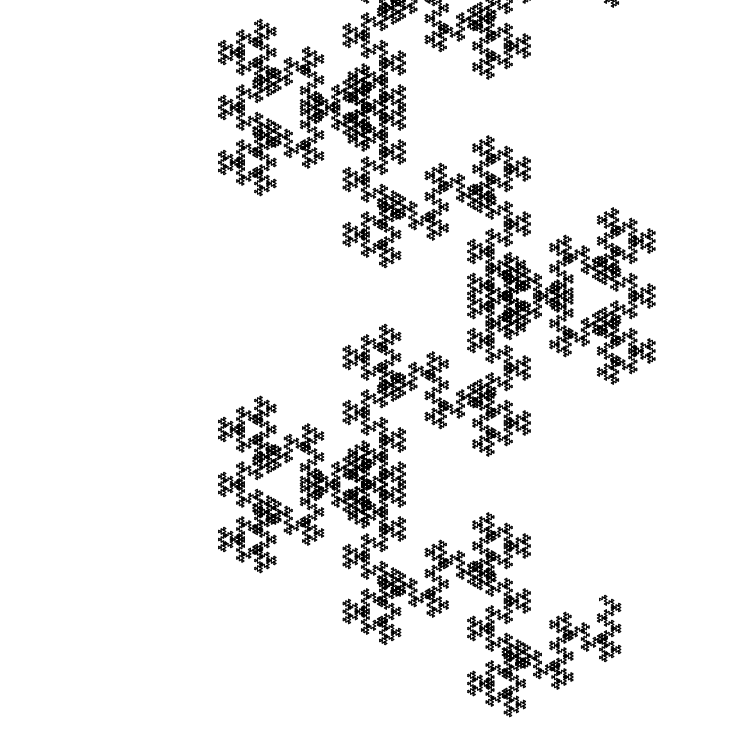
Ein anderes Beispiel sind ungerade Fibonacci-Zahlen $$$F_n$ und $$$F_ {n-3}$ .
Nimm $$$F_ {28} = 317811$ und $$$F_ {25} = 75025$ .
Sequenz:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 plus Nullbit).
Anstelle von Ecken $$$60 ^ {\ circ}$ und $$$-60 ^ {\ circ}$ Wir werden die Ecken benutzen $$$90 ^ {\ circ}$ und $$$-90 ^ {\ circ}$ .
Die Größe des Anfangssegments beträgt 5 Pixel:



Die Größe des Anfangssegments beträgt 0,4 Pixel:



Diese Kurve hat einen Namen - " Fibonacci Wort Fraktal ". Die Hausdorff-Dimension für diese Kurve ist bekannt:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}})}} = 1,6379; \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

Skript zur Visualisierung von Binärsequenzen mit Turtle Graphics

Das Problem

Ist es möglich, ein Muster für Billard zu zeichnen, dessen Seiten nicht vergleichbar sind (eine der Seiten ist eine irrationale Zahl)? Die Aufgabe ist nicht trivial. Bei dem Versuch, dieses Problem zu lösen, werden wir vor einer Reihe von Fragen stehen:

1. Wenn die Parteien nicht miteinander vereinbar sind, können wir das Billard nicht mit Zellen gleicher Größe pflastern.
2. Wenn die Seiten nicht vergleichbar sind, wird der Ball unendlich reflektiert und trifft niemals die Ecke.
3. Sequenzen in Billard werden nicht in der richtigen Reihenfolge, sondern zufällig gefüllt.



Die ersten beiden Fragen haben offensichtlich keine Lösung. Wenn es jedoch eine Möglichkeit gäbe, die Sequenz in der richtigen Reihenfolge zu füllen, könnten wir das Muster auf die oben verwendete Weise wiederherstellen, indem wir uns in der Sequenz von links nach rechts bewegen. Und damit zu sehen, wie das Muster in der oberen linken Ecke des Billard aussieht, dessen Seiten nicht vergleichbar sind.

Schwarze Magie

Nehmen Sie Billard, dessen Seiten den Fibonacci-Zahlen entsprechen (bei anderen Zahlen funktioniert ein solcher Trick möglicherweise nicht). Führen Sie den Ball hinein und fixieren Sie die Nummer des Balls, der die obere Wand berührt. Malen Sie die Zahlen mit weißer Farbe - wenn sich der Ball von rechts nach links und schwarz bewegte - wenn sich der Ball von links nach rechts bewegte:



Die weiße Farbe entspricht eins in der Sequenz, schwarz - null. Ordnen wir nun die Zahlen der Reihe nach an:



Wir haben genau die gleiche Folge von Einsen und Nullen.


In einigen Fällen müssen wir den Rest der Division nicht übernehmen. Für Fibonacci-Zahlen reicht es aus, die Parität des ganzzahligen Teils der Division zu überprüfen $$$2kN$ auf $$$M$ ::

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Im Zähler haben wir $$$F_ {n}$ . Im Nenner - $$$F_ {n + 1}$ .

Wie bekannt:

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$ - Der goldene Schnitt. Irrationale Zahl. Jetzt können wir unsere Formel schreiben als:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Wir haben eine Formel, mit der wir die Reihenfolge für Billard füllen können, deren Breite gleich ist $$$\ Phi$ und Höhe $$$1$ . Sequenzlänge = $$$\ infty$ Aber wir können einen Teil des Musters wiederherstellen, indem wir uns nacheinander von links nach rechts bewegen und in die obere linke Ecke des Billards schauen. Es bleibt abzuwarten, wie man zählt $$$\ Phi$

Die durch den goldenen Schnitt geteilte Einheit kann wie folgt umgeschrieben werden:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

Wir können zwei loswerden:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}})} {2} = k \ sqrt {5} -k$$

Unsere Formel hat die Form:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Aus Gründen der Klarheit habe ich einen Tisch gezeichnet. In der dritten Spalte verwerfen wir den Bruchteil und verlassen das Ganze. In der vierten Spalte überprüfen wir die Parität des ganzzahligen Teils:



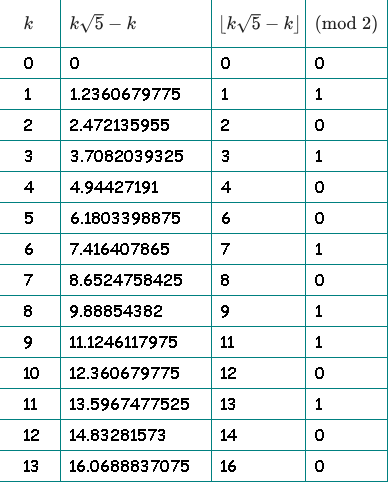
In der vierten Spalte haben wir unsere Sequenz bekommen: 01010010110100 ...

Wir berechnen weiterhin die Bits für den Rest $$$k$ . Restaurierung eines Teils des Billardmusters mit Seiten $$$1$ und $$$\ Phi$ ::



Wenn Sie nicht jedes Mal mitnehmen $$$k$ - dann wird jedes zweite Bit in der Sequenz invertiert. Wir erhalten die allgemeine Formel:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Was hindert uns daran, die Quadratwurzel von drei oder beispielsweise von zwei anstelle der Quadratwurzel von fünf zu verwenden? Nichts.

Wir konstruieren eine Sequenz für $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

Die ersten Bits der Sequenz:
00100101101001001011010010110110100101101001001011010010010110100101 ...

Wir werden mit Schildkrötengrafiken visualisieren. Winkel von 90 und -90 Grad. Die anfängliche Segmentgröße beträgt 5 Pixel:



Die Größe des Anfangssegments beträgt 0,5 Pixel:



Wir konstruieren eine Sequenz für $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

Die ersten Bits der Sequenz ( A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...

Winkel von 90 und -90 Grad. Die anfängliche Segmentgröße beträgt 5 Pixel:



Die Größe des Anfangssegments beträgt 0,5 Pixel:





Winkel von 60 und -60 Grad. Die anfängliche Segmentgröße beträgt 5 Pixel:



Visualisierungsskript

Jemand kann bezweifeln, dass die Parität des ganzzahligen Teils von $$$k \ sqrt {2}$ gibt eine fraktale Sequenz. Wir visualisieren einen Teil dieser Sequenz auf die zweite Weise:



Aus Gründen der Klarheit habe ich die längste Kurve im resultierenden Muster übermalt:



Diese Kurve hat einen Namen - "Fibonacci Wort Fraktal".

Wie bekomme ich diese Sequenz mit Billard? Wir nehmen Billard, dessen Breite = 1 und Höhe = $$$\ sqrt {2}$ . An den oberen und unteren Grenzen legen wir die Bewegungsrichtung des Balls fest. Wenn sich der Ball von links nach rechts bewegt hat - schreiben Sie 0, wenn von rechts nach links - schreiben Sie 1.



Zwei Grafiken:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2)$$

Sie können sehr lange in dieser Richtung weitermachen - Muster haben viele interessante Eigenschaften. Aber der Artikel war schon zu umständlich. Ich werde am Ende über eine der interessanten Eigenschaften berichten.