
Während der Entwicklung des
Meshoptimizers stellt sich häufig die Frage: "Kann dieser Algorithmus SIMD verwenden?"
Die Bibliothek ist leistungsorientiert, aber SIMD bietet nicht immer signifikante Geschwindigkeitsvorteile. Leider kann SIMD den Code weniger portabel und weniger wartbar machen. Daher ist es in jedem Fall notwendig, einen Kompromiss zu suchen. Wenn die Leistung von größter Bedeutung ist, müssen Sie separate SIMD-Implementierungen für die SSE- und NEON-Befehlssätze entwickeln und warten. In anderen Fällen müssen Sie wissen, wie sich die Verwendung von SIMD auswirkt. Heute werden wir versuchen, den Sloppy Mesh Simplifier, einen neuen Algorithmus, der kürzlich zur Bibliothek hinzugefügt wurde, mithilfe der SSEn / AVXn-Befehlssätze zu beschleunigen.
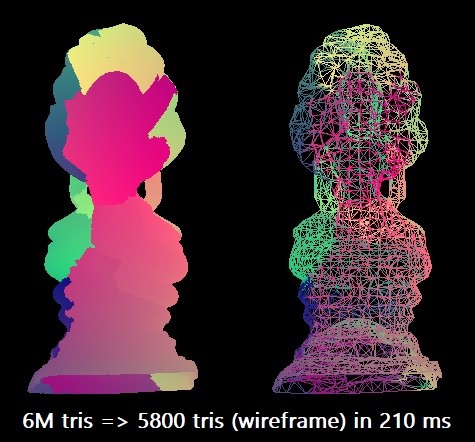
Für unseren Benchmark vereinfachen wir das thailändische Buddha-Modell von 6 Millionen Dreiecken auf 0,1% dieser Zahl. Wir verwenden den Microsoft Visual Studio 2019-Compiler für die x64-Zielarchitektur. Der Skalaralgorithmus kann eine solche Rationalisierung in etwa 210 ms in einem einzelnen Intel Core i7-8700K-Thread (bei ~ 4,4 GHz) durchführen. Dies entspricht ungefähr 28,5 Millionen Dreiecken pro Sekunde. Vielleicht reicht dies in der Praxis aus, aber ich war neugierig, die maximalen Fähigkeiten der Ausrüstung zu erkunden.
In einigen Fällen kann das Verfahren parallelisiert werden, indem das Raster in Teile geteilt wird. Dazu ist jedoch eine zusätzliche Analyse der Konnektivität erforderlich, um die Grenzen beizubehalten. Daher beschränken wir uns vorerst auf reine SIMD-Optimierungen.
Sieben Messungen
Um die Optimierungsmöglichkeiten zu verstehen, führen wir eine Profilerstellung mit Intel VTune durch. Führen Sie die Prozedur 100 Mal aus, um sicherzustellen, dass genügend Daten vorhanden sind.

Hier habe ich den Mikroarchitekturmodus aktiviert, um die Ausführungszeit jeder Funktion zu korrigieren und Engpässe zu finden. Wir sehen, dass die Rationalisierung unter Verwendung einer Reihe von Funktionen durchgeführt wird, von denen jede eine bestimmte Anzahl von Zyklen erfordert. Die Liste der Funktionen ist nach Zeit sortiert. Hier sind sie in der Reihenfolge ihrer Ausführung angeordnet, um das Verständnis des Algorithmus zu erleichtern:
rescalePositions normalisiert die Positionen aller Scheitelpunkte in einem einzigen Würfel, um die Quantisierung mit computeVertexIdscomputeVertexIds berechnet einen quantisierten 30-Bit-Bezeichner für jeden Scheitelpunkt in einem einheitlichen Raster einer bestimmten Größe, wobei jede Achse in einem Raster quantisiert wird (Rastergröße 10 Bit, der Bezeichner ist also 30).countTriangles berechnet die ungefähre Anzahl von Dreiecken, die der Innovator für eine bestimmte Gittergröße erstellt, unter der Annahme, dass alle Eckpunkte in einer Gitterzelle vereint sindfillVertexCells füllt eine Tabelle, in der alle Scheitelpunkte den entsprechenden Zellen zugeordnet sind. Alle Eckpunkte mit derselben ID entsprechen einer ZellefillCellQuadrics füllt die Quadric Struktur (symmetrische Quadric Matrix) für jede Zelle, um aggregierte Informationen über die entsprechende Geometrie QuadricfillCellRemap berechnet den Scheitelpunktindex für jede Zelle, wählt einen der Scheitelpunkte in dieser Zelle aus und minimiert die geometrische VerzerrungfilterTriangles zeigt den endgültigen Satz von Dreiecken gemäß den zuvor erstellten Vertex-Cell-Vertex-Tabellen an. Eine naive Übersetzung kann durchschnittlich ~ 5% doppelte Dreiecke erzeugen, daher filtert die Funktion doppelte.
computeVertexIds und
countTriangles werden mehrmals ausgeführt: Der Algorithmus ermittelt die Maschengröße für das Zusammenführen von Scheitelpunkten, führt eine beschleunigte binäre Suche durch, um die Zielanzahl von Dreiecken (in unserem Fall 6000) zu erreichen, und berechnet die Anzahl der Dreiecke, die jede Maschengröße bei jeder Iteration generiert. Andere Funktionen werden einmal gestartet. In unserer Datei ergeben fünf Suchdurchläufe eine Zielmaschengröße von 40
3 .
VTune berichtet hilfreich, dass die ressourcenintensivste Funktion diejenige ist, die Quadriken berechnet: Sie dauert fast die Hälfte der gesamten Ausführungszeit von 21 s. Dies ist das erste Ziel zur Optimierung von SIMD.
SIMD Stück für Stück
Schauen wir uns den Quellcode von
fillCellQuadrics an, um besser zu verstehen, was genau berechnet wird:
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } }
Die Funktion durchläuft alle Dreiecke, berechnet für jedes Dreieck ein Quadrat und fügt es den Quadriken jeder Zelle hinzu. Quadrisch - eine symmetrische 4 × 4-Matrix, dargestellt als 10 Gleitkommazahlen:
struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; };
Die Berechnung eines Quadrats erfordert das Lösen der Ebenengleichung für ein Dreieck, das Erstellen einer quadratischen Matrix und das Wiegen unter Verwendung der Fläche des Dreiecks:
static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); }
Es sieht so aus, als gäbe es viele Gleitkommaoperationen, sodass sie mit SIMD parallelisiert werden können. Zunächst stellen wir jeden Vektor als 4-breiten SIMD-Vektor dar und ändern die
Quadric in 12 Gleitkommazahlen anstelle von 10, sodass sie genau in drei SIMD-Register passt (eine Vergrößerung wirkt sich nicht auf die Leistung aus), und ändern die Reihenfolge der Felder, sodass die Berechnungen durchgeführt werden
quadricFromPlane wurde einheitlicher:
struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; };
Hier stimmen einige Berechnungen, insbesondere das Skalarprodukt, nicht sehr gut mit früheren Versionen von SSE überein. Glücklicherweise wurde in SSE4.1 eine Anweisung für ein Skalarprodukt veröffentlicht, die für uns sehr nützlich ist.
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz);
Dieser Code enthält nichts besonders Interessantes. Wir verwenden häufig nicht ausgerichtete Lade- / Speicheranweisungen. Obwohl die Eingabe von Vector3 ausgerichtet werden kann, scheint es keine merkliche Strafe für nicht ausgerichtete Lesevorgänge zu geben. Bitte beachten Sie, dass in der ersten Hälfte der Funktion keine Vektoren verwendet werden, was gut ist - unsere Vektoren haben drei Komponenten und in einigen Fällen nur eine (siehe Berechnung von Flächenq / Fläche / Entfernung), während der Prozessor 4 Operationen parallel ausführt. Lassen Sie uns auf jeden Fall sehen, wie die Parallelisierung geholfen hat.

Hundert Starts von
fillCellQuadrics jetzt in 5,3 s statt in 9,8 s, was bei jeder Operation etwa 45 ms spart - nicht schlecht, aber nicht sehr beeindruckend. In vielen Anweisungen verwenden wir drei statt vier Komponenten sowie eine präzise Multiplikation, was zu einer ziemlich signifikanten Verzögerung führt. Wenn Sie zuvor Anweisungen für SIMD geschrieben haben, wissen Sie, wie Sie das Skalarprodukt richtig ausführen.
Dazu müssen Sie vier Vektoren gleichzeitig ausführen. Anstatt einen vollständigen Vektor in einem SIMD-Register zu speichern, verwenden wir drei Register - in einem speichern wir vier Komponenten von
x , in dem anderen speichern wir
und im dritten
z . Hier werden vier Vektoren gleichzeitig für die Arbeit benötigt: Dies bedeutet, dass wir vier Dreiecke gleichzeitig verarbeiten.
Wir haben viele Arrays mit dynamischer Indizierung. Normalerweise hilft es, Daten an vorbereitete Arrays von
x /
y /
z Komponenten zu übertragen (oder vielmehr werden normalerweise kleine SIMD-Register verwendet, z. B.
float x[8], y[8], z[8] für jeden der 8 Eckpunkte in der Eingabe Daten: Dies wird als AoSoA (Arrays von Array-Strukturen) bezeichnet und bietet ein ausgewogenes Verhältnis zwischen Cache-Lokalität und einfachem Laden in SIMD-Register. Hier funktioniert die dynamische Indizierung jedoch nicht sehr gut. Laden Sie daher die Daten für vier Dreiecke wie gewohnt und transponieren Sie die Vektoren mit einem praktischen Code Makro
_MM_TRANSPOSE .
Theoretisch müssen Sie jede Komponente von vier endlichen Quadriken in einem eigenen SIMD-Register berechnen (zum Beispiel haben wir
__m128 Q_a00 mit vier Komponenten von
a00 endlichen Quadriken). In diesem Fall passen die Operationen auf den Quadriken recht gut in die 4-breiten SIMD-Anweisungen, und die Konvertierung verlangsamt den Code tatsächlich. Daher transponieren wir nur die Anfangsvektoren und transponieren dann die Ebenengleichungen zurück und führen denselben Code aus, den wir zur Berechnung der Quadriken verwendet haben, wiederholen ihn jedoch viermal. Hier ist der Code, der dann die Gleichungen der Ebene berechnet (die übrigen Teile sind der Kürze halber weggelassen):
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2];
Der Code ist etwas länger geworden: Jetzt verarbeiten wir vier Dreiecke in jeder Iteration und benötigen dafür keine SSE4.1-Anweisungen mehr. Theoretisch sollten SIMD-Einheiten effizienter eingesetzt werden. Mal sehen, wie es geholfen hat.

Okay, das ist okay. Der Code hat sich geringfügig beschleunigt, obwohl die Funktion
fillCellQuadrics jetzt fast doppelt so schnell ausgeführt wird wie die ursprüngliche Funktion ohne SIMD. Es ist jedoch unklar, ob dies eine signifikante Erhöhung der Komplexität rechtfertigt. Theoretisch können Sie AVX2 verwenden und 8 Dreiecke pro Iteration verarbeiten, aber hier müssen Sie die Schleife manuell weiter drehen (idealerweise wird der gesamte Code mit ISPC generiert, aber meine naiven Versuche, ihn zum Generieren von gutem Code zu bewegen, waren nicht erfolgreich: anstelle von Lade- / Speichersequenzen er gab beharrlich eine Sammlung / Streuung heraus, die die Ausführung erheblich verlangsamt). Versuchen wir etwas anderes.
AVX2 = SSE2 + SSE2
Der AVX2 ist ein leicht eigenwilliger Befehlssatz. Es verfügt über 8-Gleitkommaregister, und ein Befehl kann 8 Operationen ausführen. Tatsächlich unterscheidet sich ein solcher Befehl jedoch nicht von zwei SSE2-Befehlen, die auf zwei Hälften des Registers ausgeführt werden (soweit ich weiß, haben die ersten Prozessoren mit Unterstützung für AVX2 jeden Befehl in zwei oder mehr Mikrooperationen dekodiert, sodass der Leistungsgewinn durch die Phase des Extrahierens von Befehlen begrenzt war). Beispielsweise führt
_mm_dp_ps ein Skalarprodukt zwischen zwei SSE2-Registern aus, und
_mm256_dp_ps erzeugt zwei Skalarprodukte zwischen zwei Hälften von zwei AVX2-Registern, daher ist es für jede Hälfte auf 4 Breite begrenzt.
Aus diesem Grund unterscheidet sich der AVX2-Code häufig vom universellen „8-Wide-SIMD“, aber hier funktioniert er zu unseren Gunsten: Anstatt zu versuchen, die Vektorisierung durch Transponieren von 4-Wide-Vektoren zu verbessern, kehren wir zur ersten Version von SIMD zurück und verdoppeln die Schleife mithilfe von AVX2-Anweisungen anstelle von SSE2 / SSE4. Wir müssen noch 4-breite Vektoren laden und speichern, aber im Allgemeinen ändern wir nur
__m128 in
__m256 und
_mm_ in
_mm256 im
_mm256 mit mehreren Einstellungen:
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);
Hier können Sie jede 128-Bit-Hälfte der empfangenen
Qx /
Qz /
Qz und denselben Code ausführen, den wir zum Hinzufügen der Quadriken verwendet haben. Stattdessen nehmen wir an, dass wenn das Dreieck drei Eckpunkte in einer Zelle hat (
single_cell == true ), es sehr wahrscheinlich ist, dass das andere Dreieck drei Eckpunkte in einer anderen Zelle hat, und wir führen die endgültige Aggregation der Quadriken auch mit AVX2 durch:
unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else {
Der resultierende Code ist einfacher, prägnanter und schneller als unser erfolgloser SSE2-Ansatz:

Natürlich haben wir keine 8-fache Beschleunigung erreicht, sondern nur 2,45-fache. Die Lade- und Speicheroperationen sind immer noch 4-fach, da wir aufgrund der dynamischen Indizierung gezwungen sind, mit einem unangenehmen Speicherlayout zu arbeiten, und die Berechnungen für SIMD nicht optimal sind. Jetzt ist
fillCellQuadrics nicht mehr der Engpass in unserer Profil-Pipeline, und Sie können sich auf andere Funktionen konzentrieren.
Versammelt euch, Kinder
Wir haben beim Testlauf 4,8 Sekunden gespart (48 ms bei jedem Lauf), und jetzt ist unser Haupteinbruch Eindringling
countTriangles . Es scheint eine einfache Funktion zu sein, wird aber nicht einmal, sondern fünfmal ausgeführt:
static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; }
Die Funktion durchläuft alle Quelldreiecke und berechnet die Anzahl der nicht entarteten Dreiecke durch Vergleichen der Bezeichner der Scheitelpunkte. Es ist nicht sofort klar, wie es mit SIMD parallelisiert werden soll ... es sei denn, Sie verwenden die Anweisungen zum Sammeln.
Der AVX2-Befehlssatz hat die x64-SIMD um die Gather / Scatter-Befehlsfamilie erweitert. Jeder von ihnen nimmt ein Vektorregister mit 4 oder 8 Werten auf - und führt gleichzeitig 4 oder 8 Lade- oder Speicheroperationen durch. Wenn Sie hier sammeln verwenden, können Sie drei Indizes herunterladen, sammeln für alle gleichzeitig (oder in Gruppen von 4 oder 8) ausführen und die Ergebnisse vergleichen. Das Sammeln auf Intel-Prozessoren war in der Vergangenheit ziemlich langsam, aber versuchen wir es. Der Einfachheit halber laden wir Daten für 8 Dreiecke hoch, transponieren Vektoren ähnlich wie bei unserem vorherigen Versuch und vergleichen die entsprechenden Elemente jedes Vektors:
for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; }
Das Makro
_MM_TRANSPOSE8_LANE4_PS in AVX2 entspricht
_MM_TRANSPOSE4_PS , das nicht im Standardheader enthalten ist, aber einfach angezeigt werden kann. Es benötigt vier AVX2-Vektoren und transponiert zwei 4 × 4-Matrizen unabhängig voneinander:
#define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0)
Aufgrund einiger Funktionen in den SSE2 / AVX2-Befehlssätzen müssen wir beim Transponieren von Vektoren Gleitkomma-Registeroperationen verwenden. Wir laden die Daten ein wenig nachlässig; Aber im Grunde spielt es keine Rolle, denn das Sammeln von Leistung schränkt uns ein:

Jetzt ist
countTriangles ungefähr 27% schneller und bemerkt den schrecklichen CPI (Zyklen pro Anweisung): Wir senden ungefähr viermal weniger Anweisungen aus, aber das Sammeln nimmt viel Zeit in
countTriangles . Es ist großartig, dass es die Gesamtarbeit beschleunigt, aber natürlich ist der Leistungsgewinn etwas deprimierend. Wir haben es geschafft,
fillCellQuadrics im Profil zu überholen, wodurch wir zur letzten Funktion oben in der Liste gelangen, die wir noch nicht betrachtet haben.
Kapitel 6, wo alles so funktioniert, wie es sollte
Die letzte Funktion ist
computeVertexIds . In dem Algorithmus wird es 6 Mal ausgeführt, daher stellt es auch ein ausgezeichnetes Ziel für die Optimierung dar. Zum ersten Mal sehen wir eine Funktion, die für eine klare Optimierung in SIMD erstellt zu sein scheint:
static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } }
Nach den vorherigen Optimierungen wissen wir, was zu tun ist: Wickeln Sie den Zyklus vier- oder achtmal ab, da es keinen Sinn macht, nur eine Iteration zu beschleunigen, die Vektorkomponenten zu transponieren und die Berechnungen parallel auszuführen. Machen wir es mit AVX2 und verarbeiten 8 Scheitelpunkte gleichzeitig:
__m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); }
Und schauen Sie sich die Ergebnisse an: Wir haben
Wir haben computeVertexIdszweimal beschleunigt . Unter Berücksichtigung aller Optimierungen wurde die Gesamtausführungszeit des Programms auf ca. 120 ms reduziert, was der Berechnung von 50 Millionen Dreiecken pro Sekunde entspricht.Es scheint, dass wir die erwartete Produktivitätssteigerung erneut nicht erreicht haben: Sollte computeVertexIdssie nach der Parallelisierung nicht mehr als zweimal beschleunigen? Um diese Frage zu beantworten, versuchen wir herauszufinden, wie viel Arbeit diese Funktion leistet.computeVertexIdsEs wird sechsmal für einen Programmstart ausgeführt: fünfmal während der binären Suche und einmal am Ende, um die endgültigen Bezeichner zu berechnen, die für die weitere Verarbeitung verwendet werden. Jedes Mal verarbeitet diese Funktion 3 Millionen Scheitelpunkte, liest 12 Bytes für jeden Scheitelpunkt und schreibt 4 Bytes.Insgesamt verarbeitet diese Funktion in über 100 Durchläufen des Innovators 1,8 Milliarden Scheitelpunkte, liest 21 GB und schreibt 7 GB zurück. Die Verarbeitung von 28 GB in 1,46 Sekunden erfordert eine Busbandbreite von 19 GB / s. Wir können die Speicherbandbreite durch Ausführen überprüfen memcmp(block1, block2, 512 MB). Das Ergebnis sind 45 ms, dh ungefähr 22 GB / s auf einem Kern (obwohl der AIDA64-Benchmark Lesegeschwindigkeiten auf meinem System von bis zu 31 GB / s anzeigt, aber mehrere Kerne verwendet). Tatsächlich haben wir uns dem maximal erreichbaren Speicherlimit angenähert, und eine weitere Leistungssteigerung erfordert ein engeres Packen dieser Scheitelpunkte, sodass sie weniger als 12 Bytes belegen.Fazit
Wir haben einen ziemlich gut optimierten Algorithmus verwendet, der sehr große Gitter mit einer Geschwindigkeit von 28 Millionen Dreiecken pro Sekunde vereinfacht, und die Befehlssätze SSE und AVX verwendet, um sie fast zweimal auf 50 Millionen Dreiecke pro Sekunde zu beschleunigen. Während dieser Reise mussten wir verschiedene Methoden zur Verwendung von SIMD lernen: Register zum Speichern von 3-breiten Vektoren, SoA-Transposition, AVX2-Anweisungen zum Speichern von zwei 3-breiten Vektoren, Sammeln von Anweisungen zum Beschleunigen des Datenladens im Vergleich zu skalaren Anweisungen und schließlich Wir haben AVX2 direkt für die Streaming-Verarbeitung angewendet.SIMD ist oft nicht der beste Ausgangspunkt für die Optimierung: Der Mesh-Rationalisierer durchlief viele Iterationen der algorithmischen Optimierung und Mikrooptimierung, ohne plattformspezifische Anweisungen zu verwenden. Aber irgendwann sind diese Möglichkeiten ausgeschöpft, und wenn die Leistung kritisch ist, ist SIMD ein fantastisches Tool, das bei Bedarf verwendet werden kann.Ich bin mir nicht sicher, welche dieser Optimierungen in den Hauptzweig fallen werden meshoptimizer: Letztendlich ist dies nur ein Experiment, um zu sehen, wie viel der Code ohne eine radikale Änderung der Algorithmen übertaktet. Ich hoffe, dieser Artikel war informativ und gibt Ihnen Ideen zur Optimierung Ihres Codes. Die endgültigen Quellen für diesen Artikel finden Sie hier . Diese Arbeit basiert auf der Version von meshoptimizer 99ab49und das thailändische Buddha-Modell wird auf Sketchfab veröffentlicht .