Einführung
Auf Habr wurden mehrere Artikel [1,2,3] veröffentlicht, die sich direkt oder indirekt auf dieses Thema beziehen. In diesem Zusammenhang ist die Veröffentlichung [1] mit dem Titel „Mathematik an den Fingern: Linear-Quadratischer Regler“ zu übersehen, die im Volksmund das Funktionsprinzip des optimalen LQR-Reglers erklärt.
Ich wollte dieses Thema fortsetzen, nachdem ich die praktische Anwendung der dynamischen Optimierungsmethode untersucht hatte, aber bereits an einem konkreten Beispiel mit Python. Zunächst einige Worte zur Terminologie und Methode der dynamischen Optimierung.
Optimierungsmethoden werden in statische und dynamische unterteilt. Das Steuerobjekt befindet sich unter dem Einfluss verschiedener externer und interner Faktoren in einem kontinuierlichen Bewegungszustand. Daher wird die Auswertung des Regelergebnisses für die Regelzeit T gegeben, und dies ist die Aufgabe der dynamischen Optimierung.
Mit Methoden der dynamischen Optimierung werden Probleme im Zusammenhang mit der Verteilung begrenzter Ressourcen über einen bestimmten Zeitraum gelöst und die Zielfunktion als integrale Funktion geschrieben.
Der mathematische Apparat zur Lösung solcher Probleme sind Variationsmethoden: klassische Variationsrechnung, das Prinzip des maximalen L.S. Pontryagin und dynamische Programmierung R. Bellman.
Die Analyse und Synthese von Steuerungssystemen erfolgt im Zeit-, Frequenz- und Zustandsraum. Die Analyse und Synthese von Steuerungssystemen im Zustandsraum wird in den Lehrplan aufgenommen. Die in den Schulungsunterlagen unter Verwendung des SQR-Controllers vorgestellten Techniken sind jedoch für Matlab konzipiert und enthalten keine praktischen Analysebeispiele.
Der Zweck dieser Veröffentlichung ist es, die Methoden zur Analyse und Synthese linearer Steuerungssysteme im Zustandsraum anhand des bekannten Beispiels zur Optimierung des Steuerungssystems eines elektrischen Antriebs und eines Flugzeugs mithilfe der Programmiersprache Python zu betrachten.
Mathematische Begründung der dynamischen Optimierungsmethode
Zur Optimierung werden die Kriterien Amplitude (MO), Symmetrie (CO) und Kompromissoptimum (KO) verwendet.
Bei der Lösung von Optimierungsproblemen im Zustandsraum wird ein lineares stationäres System durch Vektormatrixgleichungen gegeben:
dotx= fracdxdt=A cdotx+B cdotu;y=C cdotx, (1)
Integrale Kriterien für minimalen Steuerenergieverbrauch und maximale Geschwindigkeit werden von den Funktionalen festgelegt:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin, (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin. (3)
Das Steuergesetz u liegt in Form einer linearen Rückkopplung auf die Zustandsvariablen x oder auf die Ausgangsvariablen y vor:
u= pmKx,u= pmKyEine solche Kontrolle minimiert die quadratischen Qualitätskriterien (2), (3). In den Beziehungen (1) ÷ (3) sind Q und R symmetrische positive definitive Matrizen der Dimension [n × n] bzw. [m × m]; K ist eine Matrix konstanter Dimensionskoeffizienten [m × n], deren Werte nicht begrenzt sind. Wenn der Eingabeparameter N weggelassen wird, wird angenommen, dass er Null ist.
Die Lösung für dieses Problem, das als Problem der linearen integralen quadratischen Optimierung (LQR-Optimierung) bezeichnet wird, im Zustandsraum wird durch den Ausdruck bestimmt:
u=R−1BTPxwobei die Matrix P die Ricatti-Gleichung erfüllen muss:
ATP+PA+PBR−1BTP+Q=0Die Kriterien (2), (3) sind ebenfalls widersprüchlich, da die Implementierung des ersten Terms eine Quelle unendlich hoher Leistung und für den zweiten eine Quelle unendlich niedriger Leistung erfordert. Dies kann durch den folgenden Ausdruck erklärt werden:
Jx= int infty0xTQxdt ,
Welches ist die Norm
Mod(x) Vektor x, d.h. ein Maß für seine Schwingung im Regelungsprozess und nimmt daher bei schnellen Transienten mit weniger Schwingung kleinere Werte an, und der Ausdruck:
Ju= int infty0uTRudtist ein Maß für die zur Steuerung verwendete Energiemenge und eine Strafe für die Energiekosten des Systems.
Die Gewichtsmatrizen Q, R und N hängen von den Bedingungen der entsprechenden Koordinaten ab. Wenn ein Element dieser Matrizen gleich Null ist, unterliegt die entsprechende Koordinate keinen Einschränkungen. In der Praxis erfolgt die Auswahl der Werte der Matrizen Q, R, N nach der Methode der Expertenschätzung, des Versuchs, des Fehlers und hängt von der Erfahrung und dem Wissen des Konstrukteurs ab.
Um solche Probleme zu lösen, wurden die folgenden MATLAB-Operatoren verwendet:
beginbmatrixR,S,E endbmatrix=lqr(A,B,Q,R,N) und
beginbmatrixR,S,E endbmatrix=lqry(Ps,Q,R,N) die die Funktionen (2), (3) durch den Zustandsvektor x oder durch den Ausgangsvektor y minimieren.
Verwaltungsobjektmodell
Ps=ss(A,B,C,D). Das Ergebnis der Berechnung ist die Matrix K der optimalen Rückkopplungen in Bezug auf die Zustandsvariablen x, die Lösung der Ricatti-Gleichung S und die Eigenwerte E = eiq (A-BK) des Regelungssystems.
Funktionskomponenten:
Jx=x0TP1x0,Ju=x0TP2x0wobei x0 der Vektor der Anfangsbedingungen ist;
P1 und
P2 - unbekannte Matrizen, die eine Lösung der Lyapunov-Matrixgleichungen sind. Sie werden mithilfe von Funktionen gefunden.
P1=lyap(NN,Q) und
P2=lyap(NN,KTRK) ,
NN=(A+BK)TMerkmale der Implementierung der dynamischen Optimierungsmethode mit Python
Obwohl die Python Control Systems Library [4] folgende Funktionen hat: control.lqr, control.lyap, ist die Verwendung von control.lqr nur möglich, wenn das Slycot-Modul installiert ist, was ein Problem darstellt [5]. Bei Verwendung der Lyap-Funktion im Kontext einer Aufgabe führt die Optimierung zu einer control.exception.ControlArgument: Q muss ein symmetrischer Matrixfehler sein [6].
Um die Funktionen lqr () und lyap () zu implementieren, habe ich scipy.linalg verwendet:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
Übrigens sollten Sie die Kontrolle nicht ganz aufgeben, da die Funktionen step (), pol (), ss (), tf (), feedback (), acker (), place () und andere gut funktionieren.
Ein Beispiel für die LQR-Optimierung in einem elektrischen Antrieb
(Ein Beispiel stammt aus der Publikation [7])Betrachten Sie die Synthese eines linear-quadratischen Reglers, der das Kriterium (2) für ein im Zustandsraum durch Matrizen definiertes Steuerobjekt erfüllt:
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
Folgendes wird als Zustandsvariable betrachtet:
x1 - Wandlerspannung V;
x2 - Motorstrom A;
x3 - Winkelgeschwindigkeit
c−1 . Dies ist das TP-DPT-System mit HB: Motor R nom = 30 kW; Unom = 220 V; Inom = 147 A ;;
omegaω 0 = 169
c−1 ;;
omegaω max = 187
c−1 ;; Nennwiderstandsmoment Mnom = 150 N * m; Vielzahl des Anlaufstroms = 2; Thyristorwandler: Unom = 230 V; Uy = 10 B; Inom = 300 A; Vielzahl von kurzzeitigen Überströmen = 1,2.
Bei der Lösung des Problems akzeptieren wir die Diagonale der Matrix Q. Als Ergebnis der Modellierung wurde festgestellt, dass die Minimalwerte der Matrixelemente R = 84 und
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]]. In diesem Fall wird ein monotoner Übergangsprozess der Winkelgeschwindigkeit des Motors beobachtet (Abb. 1). Bei R = 840
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]] Der Übergangsprozess (Abb. 2) erfüllt das MO-Kriterium. Die Berechnung der Matrizen P1 und P2 erfolgte bei x0 = [220 147 162].
Auflistung des Programms (Abb. 1). 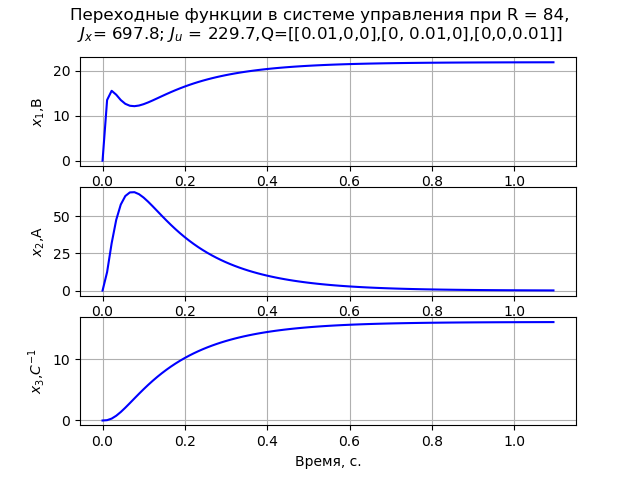 Abb. 1
Abb. 1Auflistung des Programms (Abb. 2). 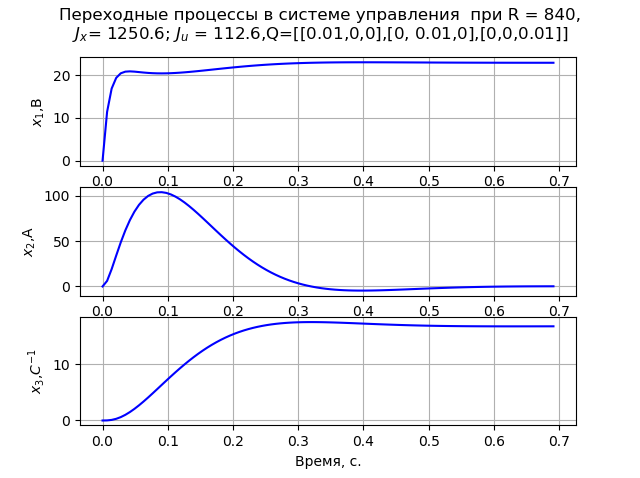 Abb. 2
Abb. 2Durch geeignete Auswahl der Matrizen R und Q ist es möglich, den Anlaufstrom des Motors auf akzeptable Werte von (2–2,5) In (Abb. 3) zu reduzieren. Zum Beispiel mit R = 840 und
Q = ([[[0,01,0,0]], [0,0,88,0], [0,0,0,01]], sein Wert beträgt 292 A und die Übergangsprozesszeit unter diesen Bedingungen beträgt 1,57 s.
Auflistung des Programms (Abb. 3). 
Abb.3
In allen betrachteten Fällen sind die Rückkopplungen von Spannung und Strom negativ und die Geschwindigkeit positiv, was gemäß den Stabilitätsanforderungen unerwünscht ist. Darüber hinaus ist das synthetisierte System für die Aufgabe astatisch und für die Last statisch. Daher betrachten wir die Synthese eines PI-Reglers im Zustandsraum mit einer zusätzlichen Zustandsvariablen
x4 - Übertragungskoeffizient des Integrators.
Wir stellen die Ausgangsinformationen in Form von Matrizen dar:
A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = Auge (4)); D = 0Aufgabentransienten, die dem MO-Kriterium entsprechen, wurden bei R = 100, q11 = q22 = q33 = 0,001 und q44 = 200 erhalten. Fig. 4 zeigt die Transienten der Zustandsvariablen, die den Astatismus des Systems nach Aufgabe und nach Last bestätigen.
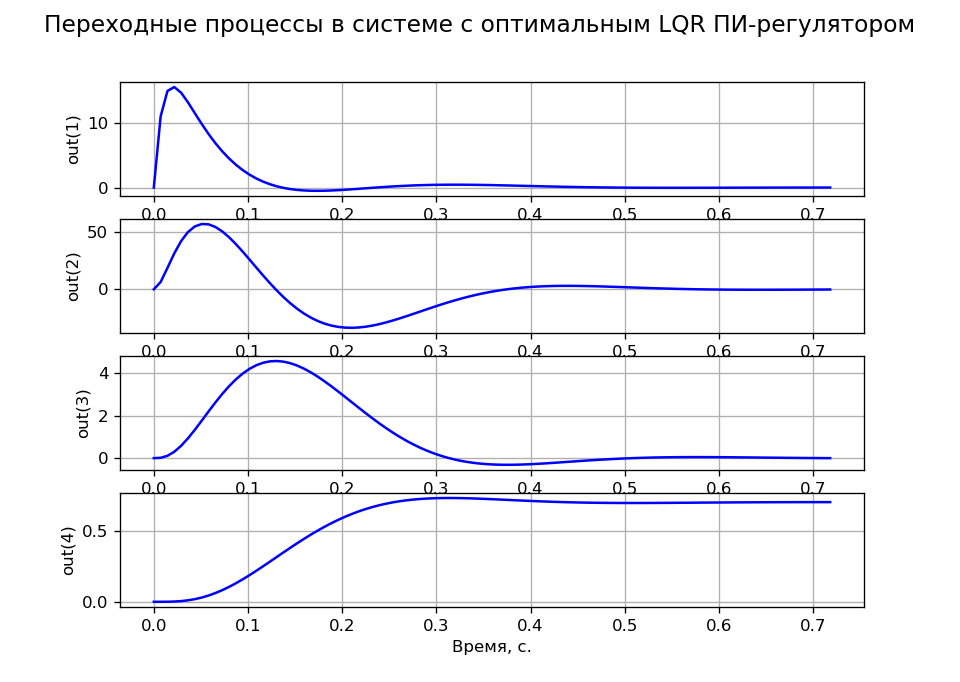 Abb. 4
Abb. 4Um die Matrix K zu bestimmen, hat die Python-Steuerungssystembibliothek zwei Funktionen: K = acker (A, B, s) und K = Ort (A, B, s), wobei s der Vektor ist - die Zeile der gewünschten Pole der Übertragungsfunktion des Regelungssystems. Der erste Befehl kann nur für Systeme mit einem Eingang in u für n ≤ 5 verwendet werden. Die zweite hat keine solchen Einschränkungen, aber die Vielzahl der Pole sollte den Rang der Matrix B nicht überschreiten. Ein Beispiel für die Verwendung des Operators acker () ist in der Auflistung und in (Abb. 5) dargestellt.
 Abb. 5
Abb. 5Fazit
Die Implementierung der in der Veröffentlichung angegebenen LQR-Optimierung des elektrischen Antriebs unter Berücksichtigung der Verwendung neuer Funktionen lqr () und lyap () ermöglicht es uns, die Verwendung des Lizenzprogramms MATLAB aufzugeben, wenn wir den entsprechenden Abschnitt der Steuerungstheorie studieren.
Ein Beispiel für die LQR-Optimierung in einem Flugzeug (LA)
(Ein Beispiel stammt aus der Veröffentlichung von Astrom und Mruray, Kapitel 5 [8] und wurde vom Autor des Artikels fertiggestellt, um die Funktion lqr () zu ersetzen und die Terminologie auf allgemein akzeptiert zu reduzieren.)Der theoretische Teil, eine kurze Theorie, die LQR-Optimierung, wurde bereits oben betrachtet. Fahren wir also mit der Code-Analyse mit den entsprechenden Kommentaren fort:
Erforderliche Bibliotheken und LQR-Controller-Funktion. from scipy.linalg import*
Anfangsbedingungen und Grundmatrizen A, B, C, D Modelle. xe = [0, 0, 0, 0, 0, 0];
Wir bauen Ein- und Ausgänge, die schrittweisen Änderungen der xy-Position entsprechen. Die Vektoren xd und yd entsprechen dem gewünschten stationären Zustand im System. Die Matrizen Cx und Cy sind die entsprechenden Ausgaben des Modells. Um die Dynamik des Systems zu beschreiben, verwenden wir ein System von Vektormatrixgleichungen:
\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ richtig.
Die Dynamik einer geschlossenen Schleife kann mit der Funktion step () für K \ cdot xd und K \ cdot xd als Eingabevektoren modelliert werden, wobei:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
Die aktuelle Steuerungsbibliothek 0.8.1 unterstützt nur einen Teil der SISO Matlab-Funktionen zum Erstellen von Rückkopplungsreglern. Um Daten vom Regler zu lesen, müssen daher Indexvektoren lat (), alt () für die laterale -x- und vertikale -y-Dynamik erstellt werden.
lat = (0,2,3,5); alt = (1,4);
Die Grafiken werden nacheinander angezeigt, eine für jede Aufgabe.
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
Grafik: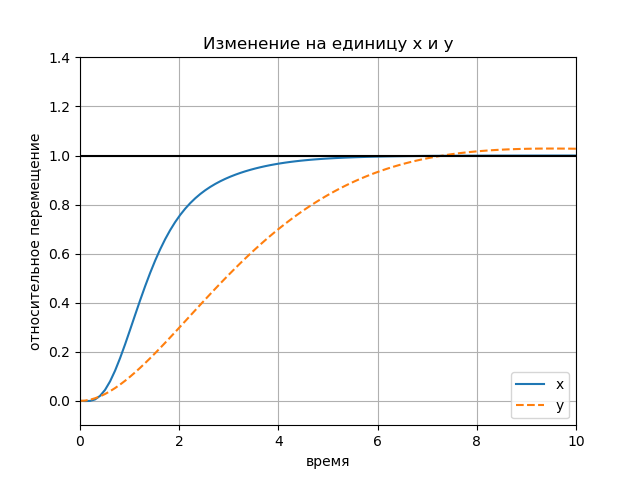
Der Einfluss der Amplitude der Eingabeaktionen Grafik: Grafik:
Grafik: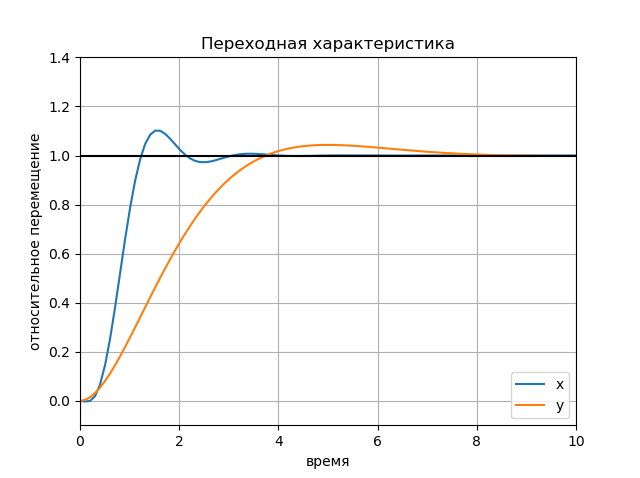
Physikalisch fundiertes Einschwingverhalten Grafik: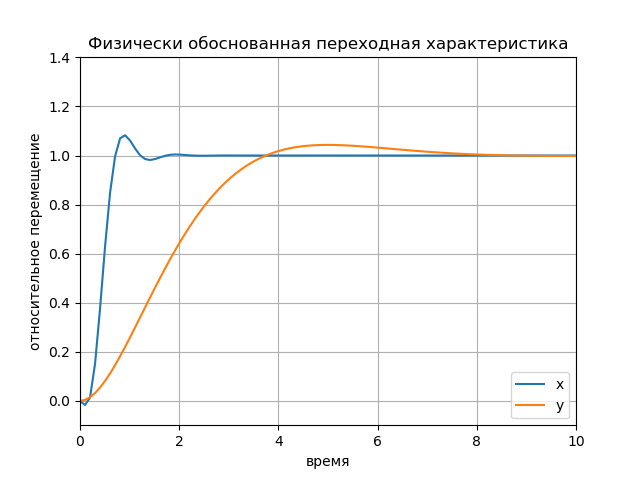
Fazit:
Die Implementierung der LQR-Optimierung in dem in der Veröffentlichung vorgestellten Flugzeug unter Berücksichtigung der Verwendung der neuen Funktion lqr () ermöglicht es uns, die Verwendung des Lizenzprogramms MATLAB beim Studium des entsprechenden Abschnitts der Steuerungstheorie aufzugeben.
Referenzen
1.
Mathematik an den Fingern: linear-quadratischer Regler.2.
Der Zustandsraum bei den Problemen des Entwurfs optimaler Steuerungssysteme.3.
Verwenden der Python Control Systems Library zum Entwerfen automatischer Steuerungssysteme.4.
Python Control Systems Library.5.
Python - Das Slycot-Modul kann nicht in Spyder (RuntimeError & ImportError) importiert werden.6.
Python Control Systems Library.7.
Kriterien für eine optimale Steuerung und LQR-Optimierung in einem elektrischen Antrieb.