Wie ein Kinderpuzzle hilft, die Geheimnisse des Magnetismus zu enthüllen

Magnete sind den Menschen seit der Antike vertraut, aber die Physik des Ferromagnetismus bleibt ein Rätsel. Jetzt bringt ein bekanntes Rätsel die Physiker der Beantwortung von Fragen näher

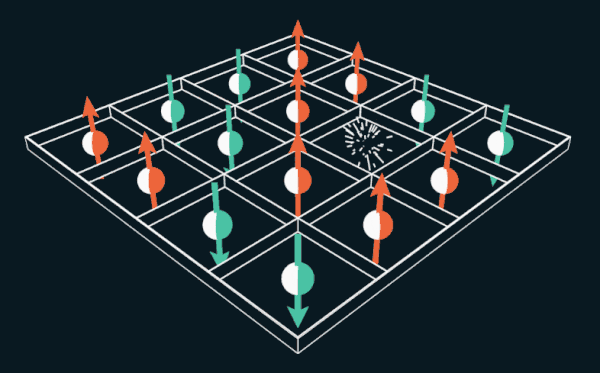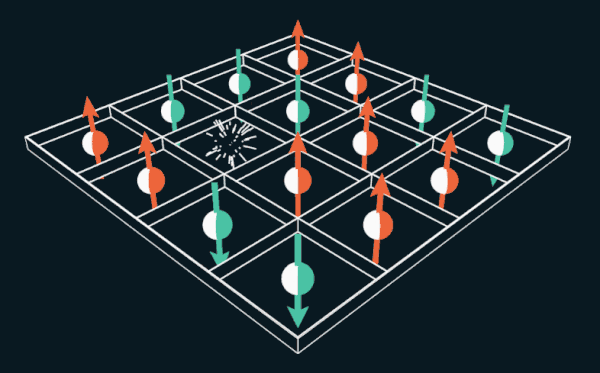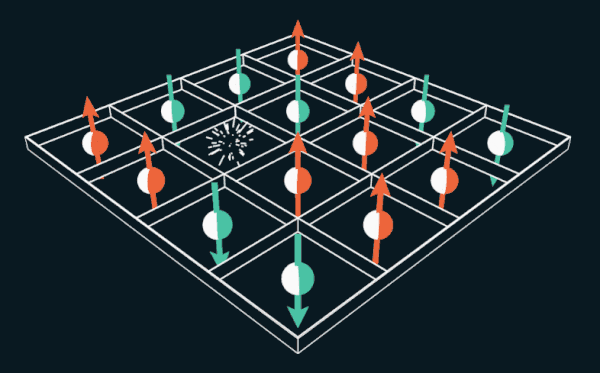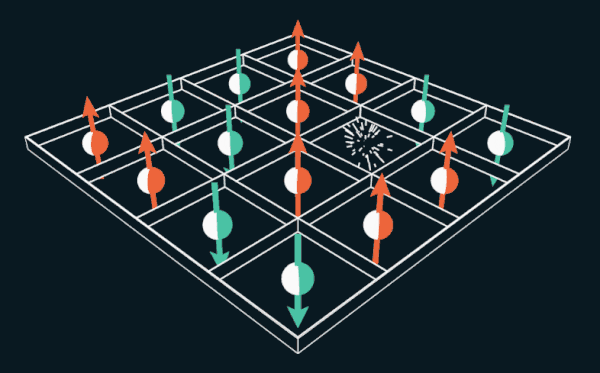Das 15er-Spiel bietet dem Spieler die Möglichkeit, die nummerierten Kacheln innerhalb des Gitters zu verschieben. Wenn Sie die Zahlen durch die Drehungen der Elektronen ersetzen, kann das Puzzle verwendet werden, um die Funktionsweise der Permanentmagnete zu erklären.

Im Jahr 1880 erlagen mehrere Monate lang ganze Regionen der Vereinigten Staaten der Sucht, deren Analoga bisher niemand gesehen hatte. "Eine Epidemie ist buchstäblich im ganzen Land ausgebrochen", schrieb die Zeitschrift The Weekly News-Democrat am 12. März 1880 in Imperia, Kansas. "Ganze Städte werden angelockt, Menschen verlieren den Schlaf und werden verrückt." Die Epidemie breitete sich auf Europa aus und erreichte sogar Australien mit Neuseeland.

Die Krankheit ist zu einer neuen Leidenschaft geworden: Entmutigung des einfachen mechanischen Puzzlespielzeugs "15". Es ist immer noch bekannt und besteht aus einem 4x4-Quadratfeld, in dem Sie 15 nummerierte Kacheln verschieben können, um sie in der richtigen Reihenfolge anzuordnen.

Nach heutigen Maßstäben scheint das Spiel altmodisch zu sein, aber 1880 war es auf dem Höhepunkt der Popularität. "Kein Kind kann einer solchen Unterhaltung widerstehen, kein Erwachsener wird so stark oder arrogant sein, um ihrem Charme zu entkommen", schrieb die Zeitung. Und die Enttäuschung könnte auf die mathematisch nachgewiesene Tatsache zurückzuführen sein, dass nur die Hälfte der Konfigurationen dieses Puzzles erfolgreich gelöst werden kann (was denjenigen, die unter seinen Einfluss gerieten, wahrscheinlich unbekannt war).

Heute, fast 140 Jahre später, hat sich das Interesse an dem Spiel "15" wieder belebt, aber diesmal ist es keine Ablenkung, sondern ein Weg zu verstehen, was damit nichts zu tun zu haben scheint und ein viel komplizierteres Rätsel: wie Magnete funktionieren.

Permanentmagnete, wie sie an der Tür Ihres Kühlschranks hängen, werden von einem Phänomen wie Ferromagnetismus angezogen. In einem Ferromagneten sind die Spins der Elektronen ausgerichtet und erzeugen zusammen ein Magnetfeld. Genauer gesagt weisen Metalle wie Eisen, Kobalt und Nickel einen Bandmagnetismus auf, da sich ihre Elektronen innerhalb des Materials frei bewegen können. Jedes Elektron hat sein eigenes magnetisches Moment, aber um zu verstehen, wie und warum all diese Momente in einem Magneten ausgerichtet sind, müssen die Quantenwechselwirkungen zwischen allen Elektronen berechnet werden, was äußerst schwierig ist.

"Zonenmagnetismus ist tatsächlich eine der größten Herausforderungen in der theoretischen Physik der kondensierten Materie", sagte Wai Lee, Physiker an der Johns Hopkins University.

Lee und zwei Doktoranden, Eric Bobrov und Keaton Stewbis, sind der Lösung dieses Problems möglicherweise etwas näher gekommen. Mit dem mathematischen Puzzle "15" erweiterten sie den bekannten Satz, der den idealisierten Zustand des Zonenmagnetismus beschreibt. In ihrer neuen Analyse , die in Physical Review B veröffentlicht wurde, erweitern sie den Satz, um ein breiteres und realistischeres System zu erklären, das möglicherweise zu einem genaueren Modell von Magneten führen könnte.

"Es ist ein großartiger Job", sagte Daniel Arovas , Physiker an der University of California in San Diego. "Ich mag diese Arbeit besonders, weil es zu wenige detaillierte Ergebnisse bezüglich des Zonenmagnetismus gibt und sie zu fragmentiert sind."

Lochspringen

Im einfachsten Fall müssen Elektronen in einem Metall zwei Hauptbeschränkungen unterliegen. Erstens sind sie alle negativ geladen, deshalb stoßen sie sich gegenseitig ab. Zweitens sind Elektronen erforderlich, um den sogenannten zu gehorchen das Pauli-Prinzip, das postuliert, dass zwei Teilchen [mit einem halbzahligen Spin / ca. trans.] kann nicht im gleichen Quantenzustand sein. Dies bedeutet, dass Elektronen mit demselben Spin - proportional zum magnetischen Moment eines Elektrons - in einem Metallatom nicht denselben Zustand einnehmen können. Und zwei Elektronen mit entgegengesetzten Spins können.

Es stellt sich heraus, dass der einfachste Weg, um sowohl die gegenseitige Abstoßung als auch die Einschränkungen des Pauli-Prinzips für eine Gruppe von Elektronen zu erfüllen, darin besteht, die Spins getrennt und auszurichten - wodurch das Material ferromagnetisch wird.

Dies ist jedoch nur ein vereinfachtes Bild. Die Physiker konnten aus unzähligen Quantenwechselwirkungen zwischen einzelnen Elektronen kein detailliertes Modell für das Auftreten eines solchen organisierten Musters ausgerichteter Spins erstellen. Zum Beispiel kann, wie Lee erklärte, die Wellenfunktion eines Elektrons - eine komplexe mathematische Beschreibung seiner Quanteneigenschaften - mit der Wellenfunktion eines anderen Elektrons verwechselt werden. Um genau zu verstehen, wie das Verhalten einzelner Teilchen zum Auftreten eines solchen kollektiven Phänomens wie Ferromagnetismus führt, müssen Sie die Wellenfunktion jedes Elektrons im System überwachen, während es die Wellenfunktion jedes der verbleibenden Elektronen im Verlauf ihrer Wechselwirkung kontinuierlich ändert. In der Praxis macht es diese allgegenwärtige Verschränkung unmöglich, die vollständigen und umfassenden Gleichungen aufzuschreiben, die zur Beschreibung des Ferromagnetismus erforderlich sind.

Stattdessen versuchen Physiker, einschließlich Lee, Informationen zu sammeln, indem sie vereinfachte, idealisierte Modelle untersuchen, die die Physik hinter dem Ferromagnetismus beschreiben. Insbesondere erweitert ihre neueste Arbeit eine wichtige Entdeckung, die vor mehr als 50 Jahren gemacht wurde.

Mitte der 1960er Jahre haben zwei Physiker von verschiedenen Seiten der Welt unabhängig voneinander Beweise dafür abgeleitet, warum sich Elektronen ausrichten und einen ferromagnetischen Zustand erzeugen sollten. David Tules, damals Physiker an der Universität Cambridge, der schließlich den Nobelpreis 2016 gewinnen sollte, und Yosuke Nagaoka, Physiker an der Nagoya University, der zu dieser Zeit die California University in San Diego besuchte, veröffentlichten ihre Beweise 1965 bzw. 1966. . Ihr Ergebnis, Nagaoki-Tules-Theorem (oder einfach Nagaoki-Theorem) genannt, basiert auf einem idealisierten Elektronensystem, das sich auf einem Atomgitter befindet. Obwohl dies das Verhalten realer Magnete nicht erklärt, war es dennoch wichtig, zum ersten Mal im Prinzip zu zeigen, warum Elektronenspins ausgerichtet werden sollten. Und da ihre Analyse mathematische Beweise waren, waren sie genau und nicht mit für die Physik typischen Annäherungen belastet.

Um den Satz zu verstehen, stellen Sie sich ein zweidimensionales quadratisches Gitter vor. Jeder Knoten kann zwei Elektronen mit entgegengesetzten Spins platzieren, aber der Satz legt nahe, dass das Platzieren von zwei Elektronen an einem Ort eine unendliche Energiemenge erfordert. Dies stellt sicher, dass sich nur ein Elektron an jedem Ort befindet. In dieser Konfiguration kann jedes Elektron seinen Spin entweder nach oben oder nach unten lenken. Sie müssen nicht ausgerichtet werden, daher sollte ein solches System kein Ferromagnet sein.


Wai Lee, Physiker an der Johns Hopkins University

Jetzt entfernen wir ein Elektron. Infolgedessen wird es einen freien Platz geben, der als Loch bezeichnet wird. Ein benachbartes Elektron kann in ein Loch rutschen und einen neuen leeren Raum hinterlassen. Ein anderes Elektron kann sich an einen neuen leeren Ort bewegen und ein weiteres Loch zurücklassen. In diesem Beispiel springt ein Loch tatsächlich von einem Ort zum anderen und bewegt sich um das Gitter herum. Thules und Nagaoka fanden heraus, dass sich in diesem Fall die Elektronen spontan ausrichten, wenn ein einzelnes Loch hinzugefügt wird. Sie bewiesen, dass es der Zustand mit der geringsten Energie sein würde, der Zustand eines Ferromagneten.

Arovas erklärt, dass ein Loch sich frei bewegen kann, ohne die Konfiguration der Elektronenspins zu stören, damit ein System in den Zustand mit der niedrigsten Energie versetzt werden kann - ein solcher Prozess erfordert zusätzliche Energie. Wenn sich ein Loch bewegt, müssen sich auch Elektronen bewegen. Damit sich die Elektronen bewegen können, ohne die Konfiguration der Spins zu stören, müssen sie ausgerichtet sein.

"Das Nagaoka-Theorem ist eines der wenigen Beispiele, die einzelne Fälle von Ferromagnetismus mathematisch beweisen können", sagte Masaki Oshikawa , Physiker an der Universität von Tokio. "Aber aus physikalischer Sicht ist das alles sehr künstlich."

Zum Beispiel benötigen Elektronen viel Energie, um ihre gegenseitige Abstoßung zu überwinden und sich an einem Ort niederzulassen - aber nicht unendlich, wie es der Satz erfordert. Darüber hinaus gilt das von Nagaoka und Tules gezeichnete Bild nur für einfache Gitter: zweidimensionale Gitter, die aus Quadraten oder Dreiecken bestehen, oder für dreidimensionale kubische Gitter. In der Natur tritt Ferromagnetismus in vielen Metallen mit Strukturen jeglicher Art auf.

Wenn der Satz von Nagaoka-Tules tatsächlich den Ferromagnetismus erklärt, sollte er auf alle Gitter anwendbar sein. Die Leute nahmen an, dass es war, sagte Lee. "Aber niemand hat echte, klare Beweise gegeben." Nun, das ist immer noch so.

Fliesen mit Rücken

1989 erweiterte Hal Tasaki, Physiker an der Gakushuin University of Japan, diesen Satz, um festzustellen, dass er anwendbar ist, solange das Gitter eine mathematische Eigenschaft wie Konnektivität besitzt. Nehmen Sie den einfachen Fall eines quadratischen Gitters mit einem beweglichen Loch. Wenn Sie durch Verschieben eines Lochs eine beliebige Konfiguration von Spins reproduzieren können, wobei die Anzahl der Elektronen beibehalten wird, wobei die Spins sowohl nach oben als auch nach unten gerichtet sind, ist die Verbindungsbedingung erfüllt.

Abgesehen von quadratischen und dreieckigen Gittern und dreidimensionalen Würfeln war jedoch nicht klar, ob die verbundene Bedingung in anderen Fällen erfüllt sein würde - und daher, wie weit dieser Satz angewendet werden könnte.

Um dieses Problem zu lösen, begann Lee mit einem sechseckigen Wabengitter. Ihre Schüler Bobrov und Stubis, die an dieser Aufgabe arbeiteten, stellten fest, dass sie einer Manie des 19. Jahrhunderts ähnelt: dem Puzzle "15". Tauschen Sie die Kacheletiketten von Zahlen zu Rücken, nach oben und unten, und das Puzzle entspricht dem Nagaoki-Ferromagneten, wobei sich ein Loch entlang des Elektronengitters bewegt.

Das Puzzle ist zulässig, wenn Sie die Möglichkeit haben, die Kacheln in einer beliebigen Reihenfolge neu zu verteilen, was vollständig mit der Konnektivitätsbedingung übereinstimmt. Die Frage, ob die Verbindungsbedingung für ein gegebenes Gitter erfüllt ist, wird zur Frage, ob es möglich ist, ein äquivalentes Rätsel auf einem Gitter einer solchen Struktur zu lösen.

Es stellt sich heraus, dass der Mathematiker Richard Wilson, der jetzt am California Institute of Technology arbeitet, 1974 dieses Problem löste, indem er das Rätsel „15“ für alle Gitter zusammenfasste und löste. Als Teil des Beweises zeigte er, dass Sie auf fast allen untrennbaren Gittern (in denen alle Knoten auch nach dem Entfernen eines Knotens verbunden bleiben) die Kacheln verschieben und eine beliebige Konfiguration erhalten können, solange die Anzahl der Bewegungen gleichmäßig bleibt. Die einzige Ausnahme besteht darin, dass einzelne Polygone größer als ein Dreieck sind und ein sogenannter "Graph θnull", bei dem der Scheitelpunkt in der Mitte des Sechsecks mit zwei gegenüberliegenden Scheitelpunkten verbunden ist.

Die Forscher konnten Wilsons Beweis direkt auf das Nagaoka-Tules-Theorem anwenden. Sie haben bewiesen, dass die Konnektivitätsbedingung für ein Elektronensystem und ein einzelnes Loch in fast allen Gittern erfüllt ist, einschließlich gemeinsamer Strukturen wie zweidimensionale Waben und dreidimensionale rautenförmige Gitter. Zwei Ausnahmen - Polygone, die größer als ein Dreieck sind, und der Graph θnull - treten in realen Ferromagneten auf keinen Fall auf.

Lochexplosion

Die Verwendung des „15“ -Puzzles ist ein frischer und potenziell fruchtbarer Ansatz, sagte Sriram Shastri , Physiker an der University of California in Santa Cruz. "Ich mag die Tatsache, dass er eine neue Sprache zur Arbeit gebracht hat, eine neue Reihe von Verbindungen zur Graphentheorie", sagte er. "Ich denke, dies ist eine reiche Verbindung - in Zukunft könnte sie eine reiche Ideenquelle werden." Obwohl die Forschung einen bedeutenden Schritt nach vorne macht, bleiben Probleme bestehen.

Eine Komplikation ist, dass das Nagaoki-Tules-Theorem nicht immer funktioniert, wenn ein sich bewegendes Loch eine ungerade Anzahl von Schritten ausführen muss, während es sich entlang des Gitters bewegt, sagte Shastri. Das vielleicht auffälligste Problem ist, dass der Satz genau ein Loch erfordert - nicht mehr und nicht weniger. Metalle sind jedoch voller Löcher, sie nehmen oft bis zur Hälfte des Gitters ein.

Die Physiker versuchten jedoch, den Satz für Systeme mit vielen Löchern zu verallgemeinern. Mit numerischen Methoden haben Physiker gezeigt, dass Nagaokis Ferromagnetismus für ein quadratisches Gitter endlicher Größe zu funktionieren scheint, von denen bis zu 30% Löcher sind. In der aktuellen Arbeit verwendeten die Forscher präzise Analysetechniken für zweidimensionale Waben und für dreidimensionale rautenförmige Gitter. Der Nagaoki-Ferromagnetismus existiert offenbar, solange die Anzahl der Löcher die Anzahl der Gitterknoten im Grad 1/2 für Zellen und im Grad 2/5 für das rautenförmige Gitter nicht überschreitet.

Diese genauen Lösungen können zu einem vollständigeren Modell des Zonenmagnetismus führen. "Dies ist nur ein kleiner Schritt, um einen strengen mathematischen Ausgangspunkt für die zukünftige Forschung zu schaffen", sagte Lee.