Neuronale gewöhnliche Differentialgleichungen

Ein erheblicher Teil der Prozesse wird durch Differentialgleichungen beschrieben. Dies kann die zeitliche Entwicklung des physischen Systems, der Gesundheitszustand des Patienten, grundlegende Merkmale der Börse usw. sein. Die Daten zu solchen Prozessen sind konsistenter und kontinuierlicher Natur, in dem Sinne, dass Beobachtungen lediglich Manifestationen eines sich ständig ändernden Zustands sind.

Es gibt auch eine andere Art von seriellen Daten, nämlich diskrete Daten, z. B. NLP-Aufgabendaten. Der Status in solchen Daten variiert diskret: von einem Zeichen oder Wort zum anderen.

Jetzt werden beide Arten solcher serieller Daten normalerweise von rekursiven Netzwerken verarbeitet, obwohl sie unterschiedlicher Natur sind und unterschiedliche Ansätze zu erfordern scheinen.

Auf der letzten NIPS-Konferenz wurde ein sehr interessanter Artikel vorgestellt, der zur Lösung dieses Problems beitragen kann. Die Autoren schlagen einen Ansatz vor, den sie als neuronale ODEs bezeichnen .

Hier habe ich versucht, die Ergebnisse dieses Artikels zu reproduzieren und zusammenzufassen, um ihre Idee etwas einfacher kennenzulernen. Es scheint mir, dass diese neue Architektur neben Faltungsnetzwerken und wiederkehrenden Netzwerken durchaus einen Platz in den Standardwerkzeugen eines Datenwissenschaftlers finden könnte.

Abbildung 1: Kontinuierliche Gradienten- Backpropagation erfordert die zeitliche Lösung der erweiterten Differentialgleichung.

Die Pfeile repräsentieren die Anpassung von rückwärts propagierten Gradienten durch Gradienten aus den Beobachtungen.

Illustration aus dem Originalartikel.

Problemstellung

Es gebe einen Prozess, der einer unbekannten ODE gehorcht, und es gebe mehrere (verrauschte) Beobachtungen entlang der Flugbahn des Prozesses

$\ frac {dz} {dt} = f (z (t), t) \; (1)$

$\ {(z_0, t_0), (z_1, t_1), ..., (z_M, t_M) \} - \ text {Beobachtungen}$

So finden Sie eine Annäherung $\ widehat {f} (z, t, \ theta)$ Lautsprecherfunktionen f (z, t)

?

Betrachten Sie zunächst eine einfachere Aufgabe: Es gibt nur zwei Beobachtungen am Anfang und am Ende der Flugbahn. (z_0, t_0), (z_1, t_1)

.

Die Systementwicklung beginnt mit dem Zustand z_0, t_0

auf Zeit

mit einigen parametrisierten Dynamikfunktionen unter Verwendung einer beliebigen Evolutionsmethode von ODE-Systemen. Nachdem sich das System in einem neuen Zustand befindet $\ hat {z_1}, t_1$ wird es mit dem Staat verglichen z_1

und der Unterschied zwischen ihnen wird durch Variieren der Parameter minimiert $\ Theta$ Dynamikfunktionen.

Oder formeller in Betracht ziehen, die Verlustfunktion zu minimieren $L (\ hat {z_1})$ ::

$L (z (t_1)) = L \ Big (\ int_ {t_0} ^ {t_1} f (z (t), t, \ theta) dt \ Big) = L \ big (\ text {ODESolve} (z () t_0), f, t_0, t_1, \ theta) \ big) \; (2)$

Zu minimieren

müssen Sie die Verläufe für alle Parameter berechnen: $z (t_0), t_0, t_1, \ theta$ . Dazu müssen Sie zunächst festlegen, wie

hängt zu jedem Zeitpunkt vom Zustand ab (z (t))

$a (t) = - \ frac {\ partielles L} {\ partielles z (t)} \; (3)$

wird ein adjungierter Zustand genannt, dessen Dynamik durch eine andere Differentialgleichung gegeben ist, die als kontinuierliches Analogon der Differenzierung einer komplexen Funktion ( Kettenregel ) betrachtet werden kann:

$\ frac {da (t)} {d t} = -a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles z} \; (4)$

Die Ausgabe dieser Formel finden Sie im Anhang des Originalartikels.

Die Vektoren in diesem Artikel sollten als Kleinbuchstabenvektoren betrachtet werden, obwohl der ursprüngliche Artikel sowohl eine Zeilen- als auch eine Spaltendarstellung verwendet.

Wenn wir diffur (4) in der Zeit zurücklösen, erhalten wir eine Abhängigkeit vom Ausgangszustand z (t_0)

$\ frac {\ partielles L} {\ partielles z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles z} dt \; (5)$

Berechnung des Gradienten in Bezug auf

und $\ Theta$ können Sie sie einfach als Teil des Staates betrachten. Dieser Zustand wird als erweitert bezeichnet . Die Dynamik dieses Zustands ergibt sich trivial aus der ursprünglichen Dynamik:

$\ frac {d} {dt} \ begin {bmatrix} z \\ \ theta \\ t \ end {bmatrix} (t) = f _ {\ text {aug}} ([z, \ theta, t]): = \ begin {bmatrix} f ([z, \ theta, t]) \\ 0 \\ 1 \ end {bmatrix} \; (6)$

Dann der konjugierte Zustand zu diesem erweiterten Zustand:

$a _ {\ text {aug}}: = \ begin {bmatrix} a \\ a _ {\ theta} \\ a_t \ end {bmatrix}, a _ {\ theta} (t): = \ frac {\ partielles L} { \ partiell \ theta (t)}, a_t (t): = \ frac {\ partiell L} {\ partiell t (t)} \; (7)$

Gradient Augmented Dynamics:

$\ frac {\ partielle f _ {\ text {aug}}} {\ partielle [z, \ theta, t]} = \ begin {bmatrix} \ frac {\ partielle f} {\ partielle z} &; \ frac {\ partielle f} {\ partielle \ theta} &; \ frac {\ partielle f} {\ partielle t} \\ 0 &; 0 &; 0 \\ 0 &; 0 &; 0 \ end {bmatrix} \; (8)$

Die Differentialgleichung des konjugierten Augmented State aus Formel (4) lautet dann:

$\ frac {d a _ {\ text {aug}}} {dt} = - \ begin {bmatrix} a \ frac {\ partielle f} {\ partielle z} &; a \ frac {\ partielles f} {\ partielles \ theta} &; a \ frac {\ partielles f} {\ partielles t} \ end {bmatrix} \; (9)$

Das Lösen dieser ODE in der Zeit ergibt:

$\ frac {\ partielles L} {\ partielles z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles z} dt \; (10)$

$\ frac {\ partielles L} {\ partielles \ Theta} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles \ Theta } dt \; (11)$

$\ frac {\ partielles L} {\ partielles t_0} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles t} dt \; (12)$

Was ist mit

$\ frac {\ partielles L} {\ partielles t_1} = - a (t) \ frac {\ partielles f (z (t), t, \ theta)} {\ partielles t} \; (13)$

Gibt dem ODESolve ODE- Solver Farbverläufe in allen Eingabeparametern.

Alle Gradienten (10), (11), (12), (13) können zusammen in einem ODESolve- Aufruf mit der Dynamik des konjugierten erweiterten Zustands (9) berechnet werden.

Illustration aus dem Originalartikel.

Der obige Algorithmus beschreibt die umgekehrte Ausbreitung des Gradienten der ODE-Lösung für aufeinanderfolgende Beobachtungen.

Bei mehreren Beobachtungen auf einer Trajektorie wird alles auf die gleiche Weise berechnet, aber zum Zeitpunkt der Beobachtungen muss die Umkehrung des propagierten Gradienten mit Gradienten aus der aktuellen Beobachtung angepasst werden, wie in Abbildung 1 gezeigt .

Implementierung

Der folgende Code ist meine Implementierung von neuronalen ODEs . Ich habe es nur getan, um besser zu verstehen, was passiert. Es kommt jedoch dem sehr nahe, was im Repository der Autoren des Artikels implementiert ist. Es enthält den gesamten Code, den Sie zum Verständnis benötigen, an einer Stelle und ist etwas auskommentierter. Für reale Anwendungen und Experimente ist es immer noch besser, die Implementierung des Originalartikels durch die Autoren zu verwenden.

import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()

Zunächst müssen Sie eine Methode zur Entwicklung von ODE-Systemen implementieren. Der Einfachheit halber wird hier die Euler-Methode implementiert, obwohl jede explizite oder implizite Methode geeignet ist.

 def ode_solve(z0, t0, t1, f): """     -   """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z

Es beschreibt auch die Oberklasse einer parametrisierten Dynamikfunktion mit einigen nützlichen Methoden.

Erstens: Sie müssen alle Parameter, von denen die Funktion abhängt, in Form eines Vektors zurückgeben.

Zweitens: Es ist notwendig, die erweiterte Dynamik zu berechnen. Diese Dynamik hängt vom Gradienten der parametrisierten Funktion in Bezug auf Parameter und Eingabedaten ab. Um den Gradienten nicht mit jeder Hand für jede neue Architektur registrieren zu müssen, verwenden wir die Methode torch.autograd.grad .

 class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True ) #  grad       , #  expand   if adfdp is not None: adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0) adfdp = adfdp.expand(batch_size, -1) / batch_size if adfdt is not None: adfdt = adfdt.expand(batch_size, 1) / batch_size return out, adfdz, adfdt, adfdp def flatten_parameters(self): p_shapes = [] flat_parameters = [] for p in self.parameters(): p_shapes.append(p.size()) flat_parameters.append(p.flatten()) return torch.cat(flat_parameters)

Der folgende Code beschreibt die Vorwärts- und Rückwärtsausbreitung für neuronale ODEs . Es ist erforderlich, diesen Code vom Hauptmodul torch.nn.Module in Form der Funktion torch.autograd.Function zu trennen , da Sie in letzterem im Gegensatz zu einem Modul eine beliebige Backpropagation- Methode implementieren können. Das ist also nur eine Krücke.

Diese Funktion liegt dem gesamten Ansatz der neuronalen ODE zugrunde.

 class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0) #   , #       def augmented_dynamics(aug_z_i, t_i): """   -     t_i -   : bs, 1 aug_z_i -   : bs, n_dim*2 + n_params + 1 """ #     z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim] # Unflatten z and a z_i = z_i.view(bs, *z_shape) a = a.view(bs, *z_shape) with torch.set_grad_enabled(True): t_i = t_i.detach().requires_grad_(True) z_i = z_i.detach().requires_grad_(True) faug = func.forward_with_grad(z_i, t_i, grad_outputs=a) func_eval, adfdz, adfdt, adfdp = faug adfdz = adfdz if adfdz is not None else torch.zeros(bs, *z_shape) adfdp = adfdp if adfdp is not None else torch.zeros(bs, n_params) adfdt = adfdt if adfdt is not None else torch.zeros(bs, 1) adfdz = adfdz.to(z_i) adfdp = adfdp.to(z_i) adfdt = adfdt.to(z_i) # Flatten f and adfdz func_eval = func_eval.view(bs, n_dim) adfdz = adfdz.view(bs, n_dim) return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1) dLdz = dLdz.view(time_len, bs, n_dim) # flatten dLdz   with torch.no_grad(): ##      #    , #       adj_z = torch.zeros(bs, n_dim).to(dLdz) adj_p = torch.zeros(bs, n_params).to(dLdz) #    z  p,        adj_t = torch.zeros(time_len, bs, 1).to(dLdz) for i_t in range(time_len-1, 0, -1): z_i = z[i_t] t_i = t[i_t] f_i = func(z_i, t_i).view(bs, n_dim) #      dLdz_i = dLdz[i_t] dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #     adj_z += dLdz_i adj_t[i_t] = adj_t[i_t] - dLdt_i #      aug_z = torch.cat(( z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z) adj_t[i_t]), dim=-1 ) #  ()      aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics) #       adj_z[:] = aug_ans[:, n_dim:2*n_dim] adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params] adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:] del aug_z, aug_ans ##         #    dLdz_0 = dLdz[0] dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #  adj_z += dLdz_0 adj_t[0] = adj_t[0] - dLdt_0 return adj_z.view(bs, *z_shape), adj_t, adj_p, None

Schließen Sie diese Funktion der Einfachheit halber in nn.Module ein .

 class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]

Anwendung

Wiederherstellung der realen Dynamikfunktion (Annäherungsverifizierung)

Lassen Sie uns nun als Basistest überprüfen, ob die neuronale ODE mithilfe von Beobachtungsdaten die wahre Funktion der Dynamik wiederherstellen kann.

Dazu bestimmen wir zunächst die Dynamikfunktion der ODE, entwickeln die darauf basierende Trajektorie weiter und versuchen dann, sie aus der zufällig parametrisierten Dynamikfunktion wiederherzustellen.

Lassen Sie uns zunächst den einfachsten Fall einer linearen ODE überprüfen. Die Funktion der Dynamik ist einfach die Wirkung einer Matrix.

$\ frac {dz} {dt} = \ begin {bmatrix} -0.1 &; -1,0 \\ 1,0 &; -0.1 \ end {bmatrix} z$

Die trainierte Funktion wird durch eine Zufallsmatrix parametrisiert.

Weiter etwas ausgefeiltere Dynamik (ohne GIF, weil der Lernprozess nicht so schön ist :))
Die Lernfunktion ist hier ein vollständig verbundenes Netzwerk mit einer verborgenen Schicht.

Code

 class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)

Die Dynamikfunktion ist nur eine Matrix

 class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)

Zufällig parametrisierte Matrix

 class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)

Dynamik für anspruchsvollere Flugbahnen

 class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt

Lerndynamik in Form eines vollständig vernetzten Netzwerks

 class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10): # Create data z0 = Variable(torch.Tensor([[0.6, 0.3]])) t_max = 6.29*5 n_points = 200 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]]) times = torch.from_numpy(times_np[:, :, None]).to(z0) obs = ode_true(z0, times, return_whole_sequence=True).detach() obs = obs + torch.randn_like(obs) * 0.01 # Get trajectory of random timespan min_delta_time = 1.0 max_delta_time = 5.0 max_points_num = 32 def create_batch(): t0 = np.random.uniform(0, t_max - max_delta_time) t1 = t0 + np.random.uniform(min_delta_time, max_delta_time) idx = sorted(np.random.permutation( index_np[(times_np > t0) & (times_np < t1)] )[:max_points_num]) obs_ = obs[idx] ts_ = times[idx] return obs_, ts_ # Train Neural ODE optimizer = torch.optim.Adam(ode_trained.parameters(), lr=0.01) for i in range(n_steps): obs_, ts_ = create_batch() z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True) loss = F.mse_loss(z_, obs_.detach()) optimizer.zero_grad() loss.backward(retain_graph=True) optimizer.step() if i % plot_freq == 0: z_p = ode_trained(z0, times, return_whole_sequence=True) plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"assets/imgs/{name}/{i}.png") clear_output(wait=True) ode_true = NeuralODE(SpiralFunctionExample()) ode_trained = NeuralODE(RandomLinearODEF()) conduct_experiment(ode_true, ode_trained, 500, "linear") func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]])) ode_true = NeuralODE(func) func = NNODEF(2, 16, time_invariant=True) ode_trained = NeuralODE(func) conduct_experiment(ode_true, ode_trained, 3000, "comp", plot_freq=30)

Wie Sie sehen können, leistet Neural ODE einen ziemlich guten Beitrag zur Wiederherstellung der Dynamik. Das heißt, das Konzept als Ganzes funktioniert.
Überprüfen Sie nun ein etwas komplizierteres Problem (MNIST, haha).

Von ResNets inspirierte neuronale ODE

In ResNet'ax ändert sich der versteckte Zustand gemäß der Formel

$h_ {t + 1} = h_ {t} + f (h_ {t}, \ theta_ {t})$

wo $t \ in \ {0 ... T \}$ Ist die Blocknummer und

Dies ist eine Funktion, die von den Ebenen innerhalb des Blocks gelernt wird.

Wenn wir im Grenzfall eine unendliche Anzahl von Blöcken mit immer kleineren Schritten nehmen, erhalten wir die kontinuierliche Dynamik der verborgenen Schicht in Form einer ODE, genau wie oben.

$\ frac {dh (t)} {dt} = f (h (t), t, \ theta)$

Ausgehend von der Eingabeebene h (0)

Wir können die Ausgabeebene definieren h (T)

als Lösung für diese ODE zum Zeitpunkt T.

Jetzt können wir zählen $\ Theta$ als verteilte ( gemeinsam genutzte ) Parameter zwischen allen infinitesimalen Blöcken.

Validierung der neuronalen ODE-Architektur auf MNIST

In diesem Teil werden wir die Fähigkeit von Neural ODE testen, als Komponenten in bekannteren Architekturen verwendet zu werden.

Insbesondere werden wir die Restblöcke im MNIST-Klassifikator durch Neural ODE ersetzen.

Code

 def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")

 Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%

Nach einem sehr rauen Training in nur 5 Epochen und 6 Minuten Training hat das Modell bereits einen Testfehler von weniger als 1% erreicht. Wir können sagen, dass sich neuronale ODEs als Komponente gut in traditionellere Netzwerke integrieren lassen.

In ihrem Artikel vergleichen die Autoren diesen Klassifikator (ODE-Net) auch mit einem regulären, vollständig verbundenen Netzwerk, mit ResNet mit einer ähnlichen Architektur und mit genau derselben Architektur, in der sich der Gradient direkt durch Operationen in ODESolve ausbreitet (ohne die konjugierte Gradientenmethode) ( RK-Net).

Illustration aus dem Originalartikel.

Demnach weist ein vollständig verbundenes 1-Schicht-Netzwerk mit ungefähr der gleichen Anzahl von Parametern wie Neural ODE einen viel höheren Fehler im Test auf, ResNet mit dem gleichen Fehler hat viel mehr Parameter und RK-Net ohne die konjugierte Gradientenmethode weist einen etwas höheren Fehler auf und mit linear steigendem Speicherverbrauch (je kleiner der zulässige Fehler ist, desto mehr Schritte muss ODESolve ausführen , wodurch sich der Speicherverbrauch linear mit der Anzahl der Schritte erhöht).

Die Autoren verwenden bei ihrer Implementierung die implizite Runge-Kutta-Methode mit adaptiver Schrittgröße, im Gegensatz zur einfacheren Euler-Methode hier. Sie untersuchen auch einige Eigenschaften der neuen Architektur.

ODE-Net-Funktion (NFE Forward - die Anzahl der Funktionsberechnungen in einem direkten Durchgang)
Illustration aus dem Originalartikel.

(a) Durch Ändern des akzeptablen Niveaus des numerischen Fehlers wird die Anzahl der Schritte bei der direkten Verteilung geändert.
(b) Die für die direkte Verteilung aufgewendete Zeit ist proportional zur Anzahl der Berechnungen der Funktion.
(c) Die Anzahl der Berechnungen der Funktion für die Rückausbreitung beträgt ungefähr die Hälfte der direkten Ausbreitung, was darauf hinweist, dass das konjugierte Gradientenverfahren rechnerisch effizienter sein kann als die Ausbreitung des Gradienten direkt durch ODESolve .
(d) Da ODE-Net immer mehr trainiert wird, erfordert es immer mehr Berechnungen einer Funktion (ein immer kleinerer Schritt), die sich möglicherweise an die zunehmende Komplexität des Modells anpassen.

Versteckte generative Funktion für die Zeitreihenmodellierung

Neuronale ODE eignet sich zur Verarbeitung kontinuierlicher serieller Daten, selbst wenn der Pfad in einem unbekannten verborgenen Raum liegt.

In diesem Abschnitt werden wir experimentieren und die Erzeugung kontinuierlicher Sequenzen mit neuronaler ODE ändern und einen Blick auf den erlernten verborgenen Raum werfen.

Die Autoren vergleichen dies auch mit ähnlichen Sequenzen, die von wiederkehrenden Netzwerken erzeugt werden.

Das Experiment hier unterscheidet sich geringfügig von dem entsprechenden Beispiel im Autoren-Repository. Hier gibt es eine vielfältigere Reihe von Trajektorien.

Daten

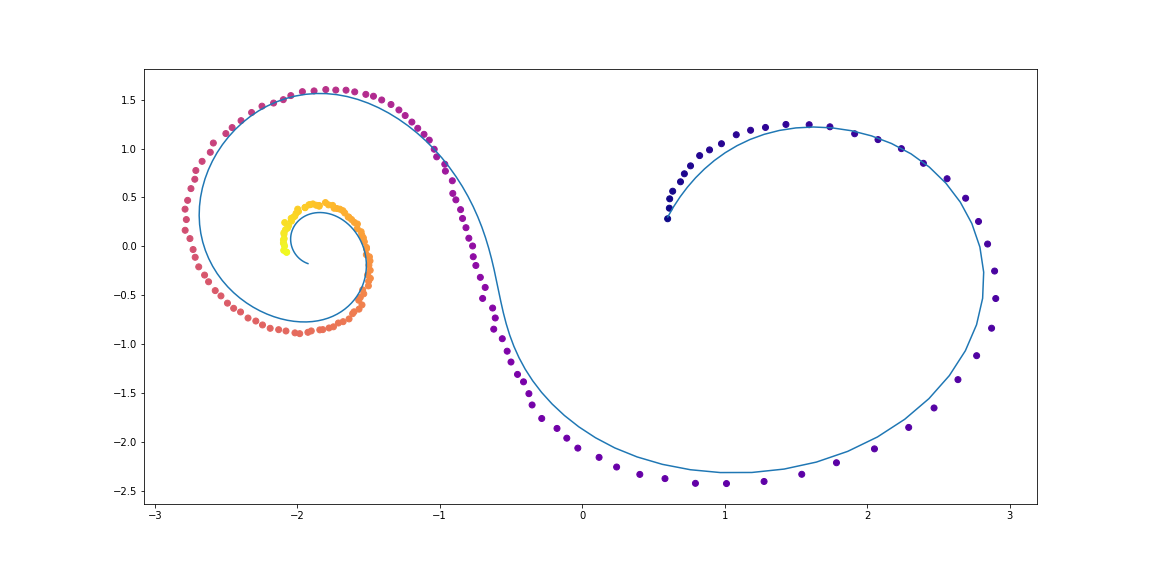
Die Trainingsdaten bestehen aus zufälligen Spiralen, von denen die Hälfte im Uhrzeigersinn und die zweite gegen den Uhrzeigersinn sind. Ferner werden zufällige Teilsequenzen aus diesen Spiralen abgetastet, die vom Codierungswiederholungsmodell in die entgegengesetzte Richtung verarbeitet werden, was zu einem verborgenen Startzustand führt, der sich dann entwickelt und eine Flugbahn im verborgenen Raum erzeugt. Dieser latente Pfad wird dann auf den Datenraum abgebildet und mit der abgetasteten Teilsequenz verglichen. Auf diese Weise lernt das Modell, Trajektorien ähnlich einem Datensatz zu generieren.

Beispiele für Datensatzspiralen

VAE als generatives Modell

Generatives Modell durch ein Stichprobenverfahren:

$z_ {t_0} \ sim \ mathcal {N} (0, I)$

$z_ {t_1}, z_ {t_2}, ..., z_ {t_M} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_M)$

$x_ {t_i} \ sim p (x \ mid z_ {t_i}; \ theta_x)$

Welches mit dem Variations-Auto-Encoder-Ansatz trainiert werden kann.

Gehen Sie durch einen wiederkehrenden Encoder durch eine Zeitsequenz in der Zeit zurück, um die Parameter zu erhalten $\ mu_ {z_ {t_0}}$ , $\ sigma_ {z_ {t_0}}$ Variations-Posterior-Verteilung und dann Probe daraus:

$z_ {t_0} \ sim q \ left (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q \ right) = \ mathcal {N} \ links (z_ {t_0} \ mid \ mu_ {z_ {t_0}} \ sigma_ {z_ {t_0}} \ rechts)$

Holen Sie sich versteckte Flugbahn:

$z_ {t_1}, z_ {t_2}, ..., z_ {t_N} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_N), \ text {where} \ frac {dz} {dt} = f (z, t; \ theta_f)$

Ordnen Sie einen versteckten Pfad einem Pfad in den Daten mithilfe eines anderen neuronalen Netzwerks zu: $\ hat {x_ {t_i}} (z_ {t_i}, t_i; \ theta_x)$
Maximieren Sie die Bewertung der unteren Gültigkeitsgrenze (ELBO) für den abgetasteten Pfad:

$\ text {ELBO} \ ungefähr N \ Big (\ sum_ {i = 0} ^ {M} \ log p (x_ {t_i} \ mid z_ {t_i} (z_ {t_0}; \ theta_f); \ theta_x) + KL \ left (q (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q) \ parallel \ mathcal {N} (0, I) \ rechts) \ Big)$

Und im Fall einer Gaußschen posterioren Verteilung $p (x \ mid z_ {t_i}; \ theta_x)$ und bekannter Geräuschpegel $\ sigma_x$ ::

$\ text {ELBO} \ ca. -N \ Big (\ sum_ {i = 1} ^ {M} \ frac {(x_i - \ hat {x_i}) ^ 2} {\ sigma_x ^ 2} - \ log \ sigma_ { z_ {t_0}} ^ 2 + \ mu_ {z_ {t_0}} ^ 2 + \ sigma_ {z_ {t_0}} ^ 2 \ Big) + C.$

Das Berechnungsdiagramm eines versteckten ODE-Modells kann wie folgt dargestellt werden

Illustration aus dem Originalartikel.

Dieses Modell kann dann getestet werden, wie es den Pfad nur unter Verwendung der anfänglichen Beobachtungen interpoliert.

Code

Modelle definieren

 class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t): # Concatenate time to input t = t.clone() t[1:] = t[:-1] - t[1:] t[0] = 0. xt = torch.cat((x, t), dim=-1) _, h0 = self.rnn(xt.flip((0,))) # Reversed # Compute latent dimension z0 = self.hid2lat(h0[0]) z0_mean = z0[:, :self.latent_dim] z0_log_var = z0[:, self.latent_dim:] return z0_mean, z0_log_var class NeuralODEDecoder(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(NeuralODEDecoder, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim func = NNODEF(latent_dim, hidden_dim, time_invariant=True) self.ode = NeuralODE(func) self.l2h = nn.Linear(latent_dim, hidden_dim) self.h2o = nn.Linear(hidden_dim, output_dim) def forward(self, z0, t): zs = self.ode(z0, t, return_whole_sequence=True) hs = self.l2h(zs) xs = self.h2o(hs) return xs class ODEVAE(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(ODEVAE, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.encoder = RNNEncoder(output_dim, hidden_dim, latent_dim) self.decoder = NeuralODEDecoder(output_dim, hidden_dim, latent_dim) def forward(self, x, t, MAP=False): z_mean, z_log_var = self.encoder(x, t) if MAP: z = z_mean else: z = z_mean + torch.randn_like(z_mean) * torch.exp(0.5 * z_log_var) x_p = self.decoder(z, t) return x_p, z, z_mean, z_log_var def generate_with_seed(self, seed_x, t): seed_t_len = seed_x.shape[0] z_mean, z_log_var = self.encoder(seed_x, t[:seed_t_len]) x_p = self.decoder(z_mean, t) return x_p

Datensatzgenerierung

 t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32) # Generate random spirals parameters normal01 = torch.distributions.Normal(0, 1.0) x0 = Variable(normal01.sample((num_spirals, 2))) * 2.0 W11 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W22 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W21 = -1.0 * normal01.sample((num_spirals,)).abs() W12 = 1.0 * normal01.sample((num_spirals,)).abs() xs_list = [] for i in range(num_spirals): if i % 2 == 1: # Make it counter-clockwise W21, W12 = W12, W21 func = LinearODEF(Tensor([[W11[i], W12[i]], [W21[i], W22[i]]])) ode = NeuralODE(func) xs = ode(x0[i:i+1], times[:, i:i+1], return_whole_sequence=True) xs_list.append(xs) orig_trajs = torch.cat(xs_list, dim=1).detach() samp_trajs = orig_trajs + torch.randn_like(orig_trajs) * noise_std samp_ts = times fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(samp_trajs[:, i, 0], samp_trajs[:, i, 1], c=samp_ts[:, i, 0], cmap=cm.plasma) plt.show() import numpy.random as npr def gen_batch(batch_size, n_sample=100): n_batches = samp_trajs.shape[1] // batch_size time_len = samp_trajs.shape[0] n_sample = min(n_sample, time_len) for i in range(n_batches): if n_sample > 0: probs = [1. / (time_len - n_sample)] * (time_len - n_sample) t0_idx = npr.multinomial(1, probs) t0_idx = np.argmax(t0_idx) tM_idx = t0_idx + n_sample else: t0_idx = 0 tM_idx = time_len frm, to = batch_size*i, batch_size*(i+1) yield samp_trajs[t0_idx:tM_idx, frm:to], samp_ts[t0_idx:tM_idx, frm:to]

Schulung

 vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")

Das passiert nach einer Nacht des Trainings

Punkte sind verrauschte Beobachtungen der ursprünglichen Flugbahn (blau),
gelb sind rekonstruierte und interpolierte Flugbahnen, wobei Punkte als Eingaben verwendet werden.

Die Farbe des Punktes zeigt die Zeit.

Rekonstruktionen einiger Beispiele sehen nicht besonders gut aus. Vielleicht ist das Modell nicht komplex genug oder nicht lange genug untersucht. In jedem Fall sieht die Rekonstruktion sehr vernünftig aus.

Nun wollen wir sehen, was passiert, wenn wir eine versteckte Variable im Uhrzeigersinn in einen Anti-Uhr-Pfad interpolieren.

Die Autoren vergleichen auch Rekonstruktionen und Pfadinterpolationen zwischen neuronaler ODE und einem einfachen rekursiven Netzwerk.

Illustration aus dem Originalartikel.

Kontinuierliche Normalisierung von Streams

Der Originalartikel bringt auch viel zum Thema Normalisieren von Streams. Normalisierende Flüsse werden verwendet, wenn Sie eine Stichprobe aus einer komplexen Verteilung erstellen müssen, die durch eine Änderung von Variablen aus einer einfachen Verteilung (z. B. Gauß) entsteht, und dennoch die Wahrscheinlichkeitsdichte am Punkt jeder Stichprobe kennen.
Die Autoren zeigen, dass die Verwendung der kontinuierlichen Variablensubstitution viel rechnerisch effizienter und interpretierbarer ist als frühere Methoden.

Das Normalisieren von Flüssen ist in Modellen wie Variation AutoCoders , Bayesian Neural Networks und anderen aus dem Bayesian-Ansatz sehr nützlich .

Dieses Thema ist jedoch über den Rahmen diesesArtikel, und diejenigen, die interessiert sind, sollten den ursprünglichen wissenschaftlichen Artikel lesen.

Für Saatgut:

Visualisierung der Transformation von Rauschen (einfache Verteilung) zu Daten (komplexe Verteilung) für zwei Datensätze;

Die X-Achse zeigt die Transformation von Dichte und Proben im Verlauf von „Zeit“ (für NS) und „Tiefe“ (für NS).

Illustration aus dem Originalartikel

Vielen Dank an bekemax für die Hilfe bei der Bearbeitung der englischen Version des Textes und für interessante physische Kommentare.

Damit ist meine kleine Forschung zu neuronalen ODEs abgeschlossen . Vielen Dank für Ihre Aufmerksamkeit!

Einführung in die neuronale ODE

Neuronale gewöhnliche Differentialgleichungen

Problemstellung

Implementierung

Anwendung

Wiederherstellung der realen Dynamikfunktion (Annäherungsverifizierung)

Von ResNets inspirierte neuronale ODE

Validierung der neuronalen ODE-Architektur auf MNIST

Versteckte generative Funktion für die Zeitreihenmodellierung

Daten

VAE als generatives Modell

Modelle definieren

Datensatzgenerierung

Schulung

Kontinuierliche Normalisierung von Streams

Nützliche Links

More articles: