Clustering von drahtlosen Zugangspunkten mithilfe der k-means-Methode

Datenvisualisierung und -analyse sind derzeit in der Telekommunikationsbranche weit verbreitet. Insbesondere hängt die Analyse stark von der Verwendung von Geodaten ab. Möglicherweise liegt dies daran, dass die Telekommunikationsnetze selbst geografisch verteilt sind. Dementsprechend kann die Analyse solcher Dispersionen von enormem Wert sein.

Daten

Zur Veranschaulichung des k-means-Clustering-Algorithmus verwenden wir die geografische Datenbank für kostenloses öffentliches WLAN in New York. Der Datensatz ist bei NYC Open Data erhältlich. Insbesondere wird der k-means-Clustering-Algorithmus verwendet, um WiFi-Nutzungscluster basierend auf Breiten- und Längengraddaten zu bilden.

Breiten- und Längengraddaten werden mit der Programmiersprache R aus dem Datensatz selbst extrahiert:

#1. Prepare data newyork<-read.csv("NYC_Free_Public_WiFi_03292017.csv") attach(newyork) newyorkdf<-data.frame(newyork$LAT,newyork$LON) 

Hier sind einige Daten:

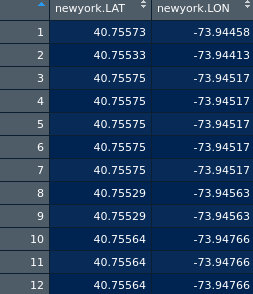
Wir bestimmen die Anzahl der Cluster

Als nächstes bestimmen wir die Anzahl der Cluster mithilfe des folgenden Codes, der das Ergebnis in einem Diagramm anzeigt.

 #2. Determine number of clusters wss <- (nrow(newyorkdf)-1)*sum(apply(newyorkdf,2,var)) for (i in 2:20) wss[i] <- sum(kmeans(newyorkdf, centers=i)$withinss) plot(1:20, wss, type="b", xlab="Number of Clusters", ylab="Within groups sum of squares") 

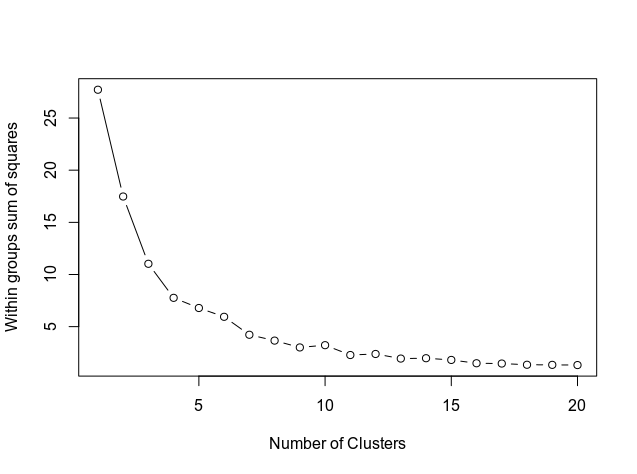
Die Grafik zeigt, wie sich die Kurve bei etwa 11 ausrichtet. Daher ist dies die Anzahl der Cluster, die im k-Mittelwert-Modell verwendet werden.

K-Mittel-Analyse

Die Analyse der K-Mittel wird durchgeführt:

 #3. K-Means Cluster Analysis set.seed(20) fit <- kmeans(newyorkdf, 11) # 11 cluster solution # get cluster means aggregate(newyorkdf,by=list(fit$cluster),FUN=mean) # append cluster assignment newyorkdf <- data.frame(newyorkdf, fit$cluster) newyorkdf newyorkdf$fit.cluster <- as.factor(newyorkdf$fit.cluster) library(ggplot2) ggplot(newyorkdf, aes(x=newyork.LON, y=newyork.LAT, color = newyorkdf$fit.cluster)) + geom_point() 

Das newyorkdf-Dataset enthält Informationen zu Breite, Länge und Clusterbezeichnung:
> newyorkdf
newyork.lat newyork.lon fit.cluster
1 40.75573 -73.94458 1
2 40.75533 -73.94413 1
3 40.75575 -73.94517 1
4 40.75575 -73.94517 1
5 40.75575 -73.94517 1
6 40.75575 -73.94517 1
...
80 40.84832 -73.82075 11

Hier ist eine klare Illustration:



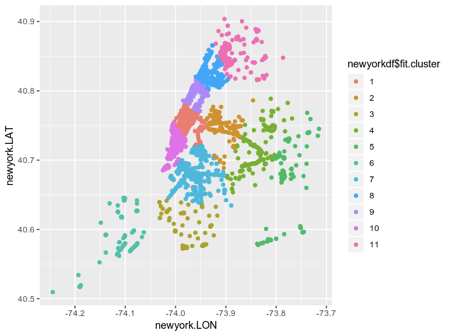
Diese Abbildung ist nützlich, aber das Rendern ist noch wertvoller, wenn Sie sie auf einer Karte von New York selbst überlagern.

 # devtools::install_github("zachcp/nycmaps") library(nycmaps) map(database="nyc") #this should also work with ggplot and ggalt nyc <- map_data("nyc") gg <- ggplot() gg <- gg + geom_map( data=nyc, map=nyc, aes(x=long, y=lat, map_id=region)) gg + geom_point(data = newyorkdf, aes(x = newyork.LON, y = newyork.LAT), colour = newyorkdf$fit.cluster, alpha = .5) + ggtitle("New York Public WiFi") 

Diese Art der Clusterbildung bietet eine hervorragende Vorstellung von der Struktur eines WiFi-Netzwerks in einer Stadt. Dies zeigt an, dass die durch Cluster 1 gekennzeichnete geografische Region viel WLAN-Verkehr aufweist. Andererseits können weniger Verbindungen in Cluster 6 auf einen geringen WLAN-Verkehr hinweisen.

K-Means-Clustering allein sagt nichts darüber aus, warum der Datenverkehr für einen bestimmten Cluster hoch oder niedrig ist. Wenn beispielsweise Cluster 6 eine hohe Bevölkerungsdichte aufweist, niedrige Internetgeschwindigkeiten jedoch zu weniger Verbindungen führen.

Dieser Clustering-Algorithmus bietet jedoch einen hervorragenden Ausgangspunkt für die weitere Analyse und erleichtert das Sammeln zusätzlicher Informationen. Anhand dieser Karte können Sie beispielsweise Hypothesen zu einzelnen geografischen Clustern erstellen. Der Originalartikel ist hier .