Aufgaben aus dem Schulbuch II

Teil I.
Teil II
Teil III

Dieser Artikel beschreibt die Methode zur Bewertung des Bereichs akzeptierter Werte und die Beziehung dieser Methode zu Aufgaben, die das Modul enthalten.

Bei der Lösung einiger Probleme muss der Bereich berücksichtigt werden, in dem der gewünschte Wert liegen kann.

Betrachten Sie die Schätzmethode zum Lösen von Ungleichungen.

Angenommen, der Preis pro Wareneinheit kann zwischen 5 und 10 RUB liegen. Eine Obergrenze anzugeben bedeutet, den Maximalwert zu bestimmen, den die gewünschte Menge annehmen kann. Für zwei Wareneinheiten, deren Preis 10 nicht überschreitet, beträgt die obere Schätzung 10 + 10 = 20 .

Betrachten Sie das Problem aus dem Problemprofilprofil MI Bashmakova
37. Bekannte Schätzungen für Variablen $$$x$ und$$ $ inline $ y: 0 <x <5, 2 <y <3. $ inline $

Geben Sie Bestnoten für die folgenden Ausdrücke:
1. $$$2x + 3y$
2. $$$xy$

5. $$$\ frac {1} {y}$
6. $$$\ frac {x} {y}$

8. $$$x-y$
9. $$$3x-2y$


Bei der Analyse infinitesimaler Größen wird im Allgemeinen ein Bewertungskriterium verwendet. Ein Modul (als Nachbarschaft) findet Anwendung in der Definition eines Grenzwerts.

$$$$ display $$ \ left | x_ {n} -a \ right | <\ varepsilon $$ display $$

Betrachten Sie das Beispiel aus dem "Verlauf der Differential- und Integralrechnung" 363 (6)

Einfache Einstellung der Zeilendivergenz

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

In der Tat, da seine Mitglieder abnehmen, die n-te Teilsumme

$$$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ display $$

und wächst ad infinitum mit $$$n$ .

Um das zu beweisen $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ wirklich mehr $$$\ sqrt {n}$ müssen Sie diesen Ausdruck niedriger schätzen. Wir erhalten das System der Ungleichungen

$$$$ display $$ \ left \ {\! \ begin {align} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {align} \ right. $$ Anzeige $$

Nachdem wir alle Ungleichungen dieses Systems hinzugefügt haben, erhalten wir

$$$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$ display $$

Dies ist ein Beweis dafür, dass diese Serie divergiert.

Für eine harmonische Reihe funktioniert diese Methode nicht, weil $$$n$ partielle partielle harmonische Reihe

$$$$ display $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ Anzeige $$

Zurück zur Aufgabe

38. Berechnen Sie den Betrag ("Aufgaben für Kinder von 5 bis 15 Jahren")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(mit einem Fehler von nicht mehr als 1% der Antwort)

Top Schätzung der Serie $$$\ frac {n} {n + 1}$ gibt die Nummer 1.

Lassen Sie den ersten Begriff fallen $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

Wir bekommen $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0,4166666666666666363
0,49019607843137253
0,4990019960079833
0,4999000199960005
0,49999000019998724
0,4999990000019941

Sie können hier in ideone.com einchecken


Löschen Sie die ersten beiden Begriffe $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

Wir erhalten 0,33333233333632745
Teilsummen der Serie sind oben begrenzt.

Die positive Zeile hat immer einen Betrag; Diese Summe ist endlich (und daher konvergiert die Reihe), wenn die Teilsummen der Reihe oben begrenzt sind, und ansonsten unendlich (und die Reihe divergiert).

Wegwerfen $$$n$ Anfangsbegriffe der harmonischen Reihe.
Beweisen Sie dies (unter Verwendung der unteren Grenze)

$$$$ Anzeige $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ $$ anzeigen

Wenn die ersten beiden Terme verworfen werden, werden die verbleibenden Mitglieder der harmonischen Reihe durch in Gruppen unterteilt $$$2,4,8, ..., 2 ^ {k-1}, ...$ Mitglieder in jedem

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...;$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...,$$

dann ist jeder dieser Beträge einzeln größer $$$\ frac {1} {2}$ .
... Wir sehen, dass Teilsummen oben nicht begrenzt werden können: Die Reihe hat eine unendliche Summe.

Wir berechnen die Teilbeträge, die durch Verwerfen erhalten werden $$$2 ^ {k}$ Begriffe.

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

Wir bekommen:
0,583333333333333434
0,6345238095238095
0,6628718503718504
Wir schreiben ein Programm, aus dem die Summe der harmonischen Reihen berechnet wird $$$\ frac {n} {2}$ vorher $$$n$ wo $$$n = 2 ^ {k}$ bei $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

Wir bekommen:
0,58333333333333333333
0,6345238095238095
0,6628718503718504
0,6777662022075267

Sie können online ide unter dem Link einchecken
Für die Reichweite $$$\ left [1 + 2 ^ {70}; 2 ^ {71} \ right]$ wir bekommen 0,693147 ...
Überprüfen Sie Mojo in Wolfram Cloud hier .

Dieser rekursive Algorithmus verursacht einen schnellen Stapelüberlauf.
Dieser Artikel enthält ein Beispiel für die Berechnung der Fakultät mithilfe eines iterativen Algorithmus. Wir modifizieren diesen iterativen Algorithmus so, dass er die Teilsumme Hn innerhalb bestimmter Grenzen berechnet; nenne diese Grenzen a und b

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

Die Untergrenze ist die Zahl $$$1 + 2 ^ {k}$ ist die Obergrenze die Zahl $$$2 \ cdot 2 ^ {k}$
Wir schreiben eine Funktion, die die Zweierpotenz berechnet

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

Wir werden (+ 1 (power_of_two k)) als untere Grenze einsetzen und die Funktion (* 2 (power_of_two k)) oder ihre äquivalente Funktion (power_of_two (+ 1 k)) als obere Grenze verwenden
Schreiben Sie die Funktion Hn neu

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

Jetzt können Sie Hn für große Werte berechnen $$$k$ .

Wir schreiben in C ein Programm, das die zur Messung von Hn erforderliche Zeit misst. Wir werden die Funktion clock () aus der Standardbibliothek <time.h> verwenden
Ein Artikel über die Messung der Prozessorzeit ist hier auf Habré.

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

Normalerweise begrenzt Online-Ide die Ausführungszeit zum Ausführen von Programmen auf fünf Sekunden, sodass dieses Programm nur in einigen Online- Ideen überprüft werden kann, z. B. onlinegdb.com oder repl.it.
Für k von 1 + 2 ^ 30 bis 2 ^ 31 beträgt die Betriebszeit ~ 5 Sekunden.
Für k von 1 + 2 ^ 31 bis 2 ^ 32 beträgt die Betriebszeit ~ 10 Sekunden.
Für k von 1 + 2 ^ 32 bis 2 ^ 33 beträgt die Betriebszeit ~ 20 Sekunden.
Für k von 1 + 2 ^ 33 bis 2 ^ 34 beträgt die Betriebszeit ~ 40 Sekunden.
Für k von 1 + 2 ^ 34 bis 2 ^ 35 beträgt die Betriebszeit mehr als eine Minute.
...
Für k von 1 + 2 ^ 45 bis 2 ^ 46 beträgt die Betriebszeit mehr als 24 Stunden.

Angenommen, für k von 1 + 2 ^ 30 bis 2 ^ 31 beträgt die Ausführungszeit des Algorithmus ~ 2 Sekunden.
Dann beträgt für k = 2 ^ (30 + n) die Ausführungszeit des Algorithmus 2 ^ n Sekunden. (at $$$n \ in \ mathbb {N}$ )
Dieser Algorithmus hat eine exponentielle Komplexität .

Zurück zu den Modulen.
In der Integralrechnung wird das Modul in der Formel verwendet

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | x \ right | + C$$

Auf Habré gab es einen Artikel Der natürlichste Logarithmus, in dem dieses Integral auf der Grundlage seiner Zahlenberechnung betrachtet wird $$$e$ .

Das Vorhandensein des Moduls in der Formel $$$\ int \ frac {dx} {x} = ln \ left | x \ right | + C$ weiter begründet im "Verlauf der Differential- und Integralrechnung"

Wenn ...$$ $ inline $ x <0 $ inline $ dann ist es durch Differenzierung leicht zu überprüfen, ob $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

Physikalische Anwendung des Integrals $$$\ int \ frac {dx} {x}$

Dieses Integral wird verwendet, um die Potentialdifferenz der Platten eines zylindrischen Kondensators zu berechnen.


"Elektrizität und Magnetismus":

Die Potentialdifferenz zwischen den Platten ergibt sich durch Integration:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limit_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limit_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ und $$$R_ {2}$ - die Radien der Innen- und Außenplatte).

Das Modulzeichen wird hier nicht unter dem Zeichen des natürlichen Logarithmus verwendet $$$ln \ left | \ frac {R_ {2}} {R_ {1}} \ right |$ , weil $$$R_ {1}$ und $$$R_ {2}$ streng positiv und diese Form der Aufzeichnung ist überflüssig.

"Modulare" Zeichnung

Mit Modulen können Sie verschiedene Formen zeichnen.

Wenn im Geogebra- Programm, schreiben Sie die Formel $$$abs (x) + abs (y) = 1$ wir bekommen



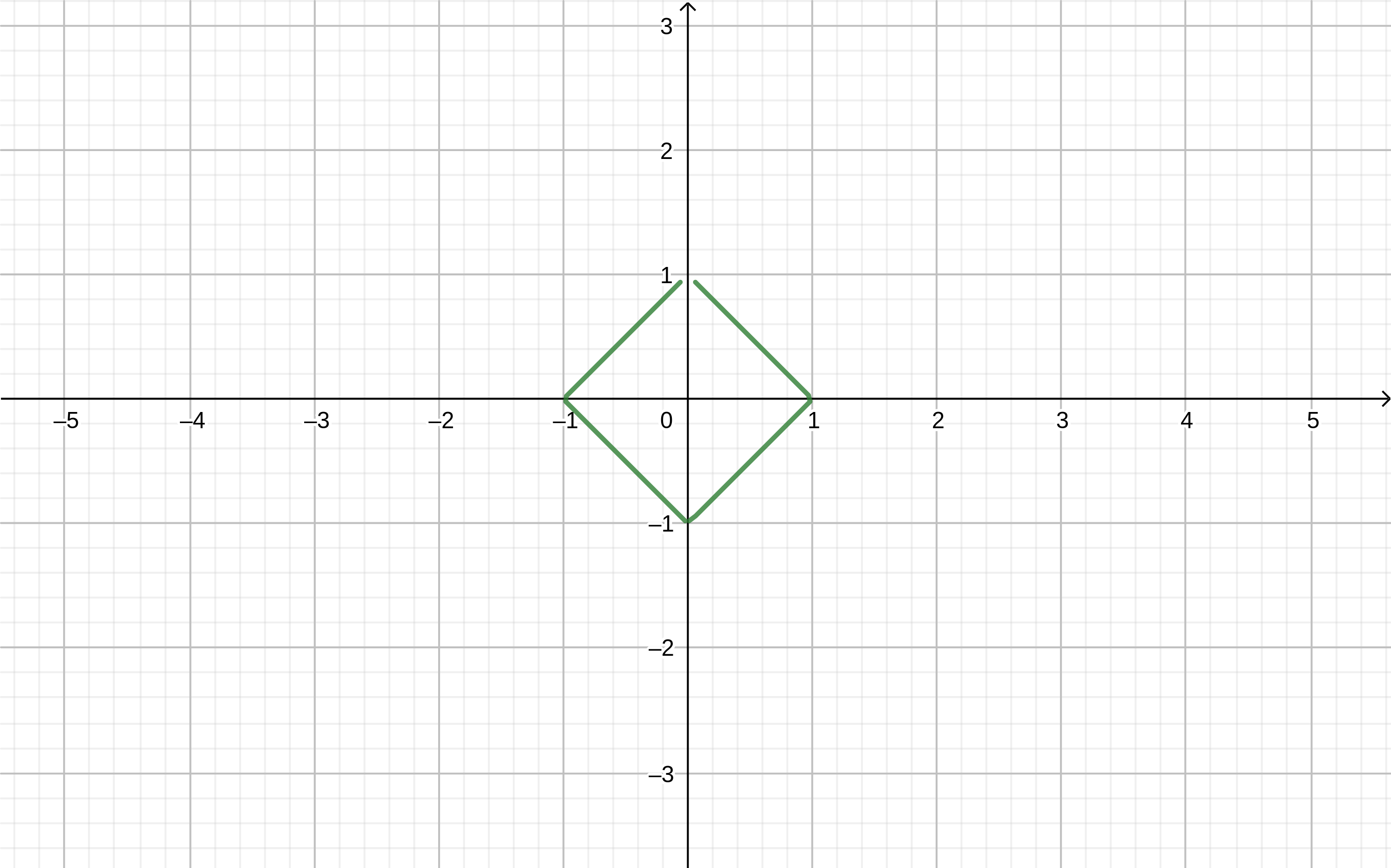
Sie können komplexere Formen zeichnen. Zeichnen wir zum Beispiel einen „Schmetterling“ in die WolframAlpha-Wolke

$$

$$\ sum \ frac {\ left | x \ right | } {n- \ left | x \ right | } + \ frac {\ left | x + n \ rechts | } {n} + \ frac {\ left | x-n \ rechts | } {n}$$

Zeichnen Sie [Summe [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60,60}]
In diesem Ausdruck $$$n$ liegt im Bereich von $$$1$ vorher $$$20$ , $$$x$ liegt im Bereich von $$$-60$ vorher $$$60$ .
Link zum Bild.

Bücher:

"Das Aufgabenbuch der Profilorientierung" M.I. Bashmakov
Allgemeiner Physikkurs: in 3 Bänden T. 2. "Elektrizität und Magnetismus" I.V. Savelyev