Hallo Habr! Ich mache Sie auf eine Übersetzung des Artikels von Rudy Gilman und Katherine Wang aufmerksam. Intuitive RL: Einführung in Advantage-Actor-Critic (A2C) .

Reinforced Learning Specialists (RL) haben viele hervorragende Tutorials erstellt. Die meisten beschreiben RL jedoch anhand mathematischer Gleichungen und abstrakter Diagramme. Wir denken gerne aus einer anderen Perspektive über das Thema nach. RL selbst ist davon inspiriert, wie Tiere lernen. Warum also nicht den zugrunde liegenden RL-Mechanismus zurück in natürliche Phänomene übersetzen, die simuliert werden sollen? Menschen lernen am besten durch Geschichten.
Dies ist die Geschichte des Actor Advantage Critic (A2C) -Modells. Das Subjekt-Kritiker-Modell ist eine beliebte Form des Policy-Gradient-Modells, das an sich ein traditioneller RL-Algorithmus ist. Wenn Sie A2C verstehen, verstehen Sie tiefes RL.
Nachdem Sie ein intuitives Verständnis von A2C erhalten haben, überprüfen Sie:
Illustrationen @embermarke
In RL bewegt sich der Agent, der Klyukovka-Fuchs, durch die von Aktionen umgebenen Staaten und versucht, die Belohnungen während der Reise zu maximieren.
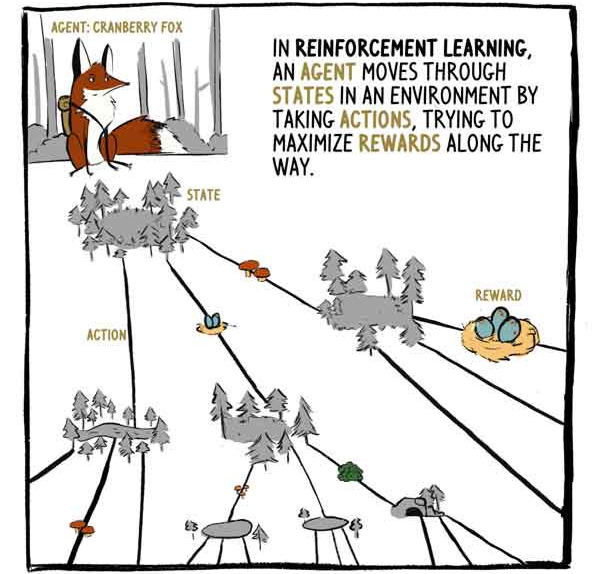
A2C empfängt Statuseingänge - Sensoreingänge bei Klukovka - und generiert zwei Ausgänge:
1) Eine Bewertung, wie viel Vergütung ab dem Zeitpunkt des aktuellen Zustands mit Ausnahme der aktuellen (bestehenden) Vergütung erhalten wird.
2) Eine Empfehlung, welche Maßnahmen zu ergreifen sind (Politik).
Kritiker: Wow, was für ein wundervolles Tal! Es wird ein fruchtbarer Tag für die Nahrungssuche! Ich wette heute sammle ich 20 Punkte vor Sonnenuntergang.
"Betreff": Diese Blumen sehen wunderschön aus, ich habe ein Verlangen nach "A".

Deep RL-Modelle sind wie jedes andere Klassifizierungs- oder Regressionsmodell Input-Output-Mapping-Maschinen. Anstatt Bilder oder Text zu kategorisieren, bringen tiefe RL-Modelle Zustände zu Aktionen und / oder Zustände zu Zustandswerten. A2C macht beides.


Diese Menge an staatlicher Handlungsbelohnung ist eine Beobachtung. Sie wird diese Datenzeile in ihr Tagebuch schreiben, aber sie wird noch nicht darüber nachdenken. Sie wird es füllen, wenn sie innehält, um nachzudenken.
Einige Autoren assoziieren Belohnung 1 mit Zeitschritt 1, andere assoziieren sie mit Schritt 2, aber alle denken an dasselbe Konzept: Die Belohnung bezieht sich auf den Zustand und die Aktion geht unmittelbar davor.

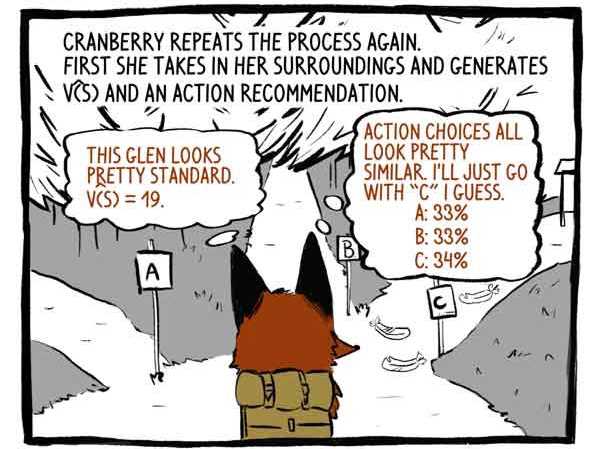
Das Einhaken wiederholt den Vorgang erneut. Zunächst nimmt sie ihre Umgebung wahr und entwickelt eine Funktion V (S) und eine Handlungsempfehlung.
Kritiker: Dieses Tal sieht ziemlich normal aus. V (S) = 19.
Betreff: Die Aktionsoptionen sehen sehr ähnlich aus. Ich denke, ich gehe einfach auf Spur "C".
Dann handelt es.

Erhält eine Belohnung von +20! Und zeichnet die Beobachtung auf.

Sie wiederholt den Vorgang erneut.

Nachdem Klyukovka drei Beobachtungen gesammelt hat, bleibt er stehen, um nachzudenken.
Andere Modellfamilien warten bis zum Ende des Tages (Monte Carlo), während andere nach jedem Schritt nachdenken (Ein-Schritte).
Bevor sie ihre interne Kritikerin einstellen kann, muss Klukovka berechnen, wie viele Punkte sie in jedem Staat tatsächlich erhalten wird.
Aber zuerst!
Schauen wir uns an, wie Klukovkas Cousine Lis Monte Carlo die wahre Bedeutung jedes Staates berechnet.
Monte-Carlo-Modelle spiegeln ihre Erfahrung erst am Ende des Spiels wider. Da der Wert des letzten Zustands Null ist, ist es sehr einfach, den wahren Wert dieses vorherigen Zustands als Summe der nach diesem Moment erhaltenen Belohnungen zu ermitteln.
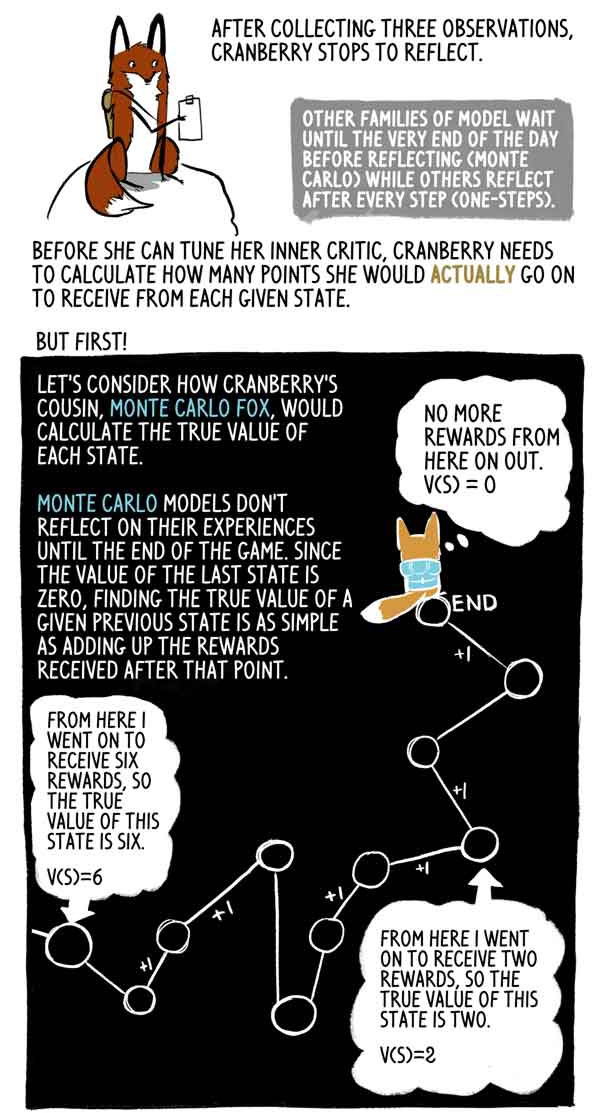
Tatsächlich ist dies nur eine Probe V (S) mit hoher Dispersion. Der Agent könnte leicht einer anderen Flugbahn aus demselben Zustand folgen und somit eine andere Gesamtbelohnung erhalten.
Aber Klyukovka geht, bleibt stehen und reflektiert viele Male, bis der Tag zu Ende geht. Sie möchte wissen, wie viele Punkte sie wirklich von jedem Staat bis zum Ende des Spiels erhalten wird, da bis zum Ende des Spiels noch einige Stunden verbleiben.
Dort macht sie etwas wirklich Kluges - der Fuchs Klyukovka schätzt, wie viele Punkte sie für den letzten Staat in diesem Set erhalten wird. Glücklicherweise hat sie eine korrekte Einschätzung ihres Zustands - ihren Kritiker.
Mit dieser Einschätzung kann Klyukovka die „richtigen“ Werte der vorherigen Zustände genau wie der Monte-Carlo-Fuchs berechnen.
Lis Monte Carlo wertet die Zielmarken aus, setzt die Flugbahn ein und fügt Belohnungen aus jedem Zustand hinzu. A2C schneidet diese Flugbahn und ersetzt sie durch eine Einschätzung seines Kritikers. Diese anfängliche Belastung verringert die Varianz der Punktzahl und ermöglicht es dem A2C, kontinuierlich zu laufen, wenn auch durch Einführen einer kleinen Vorspannung.

Die Prämien werden häufig reduziert, um der Tatsache Rechnung zu tragen, dass die Vergütung jetzt besser ist als in der Zukunft. Der Einfachheit halber reduziert Klukovka seine Belohnungen nicht.

Klukovka kann nun jede Datenzeile durchgehen und seine Schätzungen der Zustandswerte mit seinen tatsächlichen Werten vergleichen. Sie nutzt den Unterschied zwischen diesen Zahlen, um ihre Vorhersagefähigkeiten zu perfektionieren. Klyukovka sammelt den ganzen Tag über alle drei Schritte wertvolle Erfahrungen, die es wert sind, in Betracht gezogen zu werden.
„Ich habe die Zustände 1 und 2 schlecht bewertet. Was habe ich falsch gemacht? Ja! Wenn ich das nächste Mal solche Federn sehe, werde ich V (S) erhöhen.
Es mag verrückt erscheinen, dass Klukovka ihre V (S) -Bewertung als Grundlage für den Vergleich mit anderen Prognosen verwenden kann. Aber Tiere (einschließlich uns) tun dies die ganze Zeit! Wenn Sie das Gefühl haben, dass die Dinge gut laufen, müssen Sie die Aktionen, die Sie in diesen Zustand gebracht haben, nicht neu trainieren.

Durch Trimmen unserer berechneten Ausgaben und Ersetzen durch eine anfängliche Lastschätzung haben wir die große Monte-Carlo-Varianz durch eine kleine Abweichung ersetzt. RL-Modelle leiden normalerweise unter einer hohen Streuung (die alle möglichen Pfade darstellt), und ein solcher Austausch lohnt sich normalerweise.
Klukovka wiederholt diesen Vorgang den ganzen Tag, sammelt drei Beobachtungen der staatlichen Handlungsbelohnung und reflektiert sie.
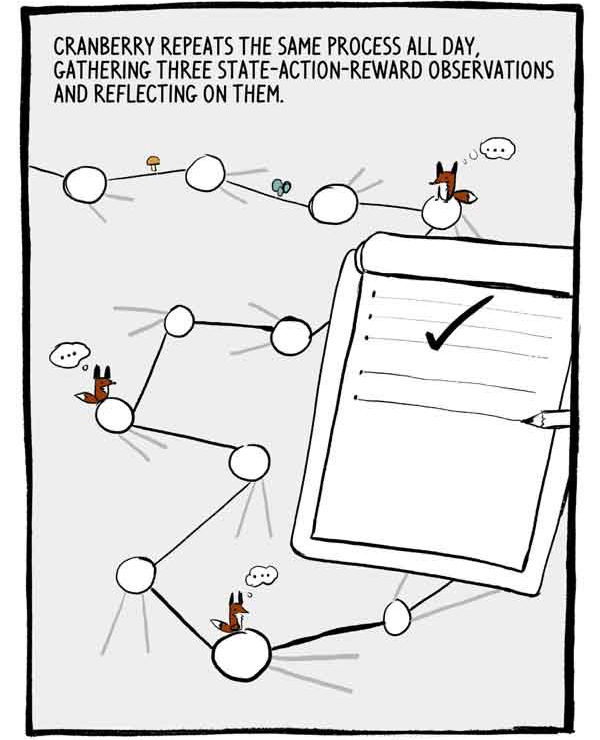
Jeder Satz von drei Beobachtungen ist eine kleine, autokorrelierte Reihe von markierten Trainingsdaten. Um diese Autokorrelation zu verringern, trainieren viele A2Cs viele Agenten parallel und addieren ihre Erfahrungen, bevor sie sie an ein gemeinsames neuronales Netzwerk senden.

Der Tag geht endlich zu Ende. Nur noch zwei Schritte.
Wie bereits erwähnt, werden die Empfehlungen der Maßnahmen von Klukovka in prozentualem Vertrauen in seine Fähigkeiten ausgedrückt. Anstatt nur die zuverlässigste Wahl zu treffen, wählt Klukovka aus dieser Verteilung von Aktionen. Dies stellt sicher, dass sie nicht immer sicheren, aber möglicherweise mittelmäßigen Handlungen zustimmt.
Ich könnte es bereuen, aber ... Manchmal kann man bei der Erforschung unbekannter Dinge zu aufregenden neuen Entdeckungen kommen ...

Um die Forschung weiter zu fördern, wird ein Wert namens Entropie von der Verlustfunktion abgezogen. Entropie bedeutet den „Umfang“ der Verteilung von Aktionen.
- Es scheint, dass sich das Spiel ausgezahlt hat!

Oder nicht?
Manchmal befindet sich der Agent in einem Zustand, in dem alle Aktionen zu negativen Ergebnissen führen. A2C kommt jedoch mit schlechten Situationen gut zurecht.


Als die Sonne unterging, dachte Klyukovka über die letzten Lösungen nach.

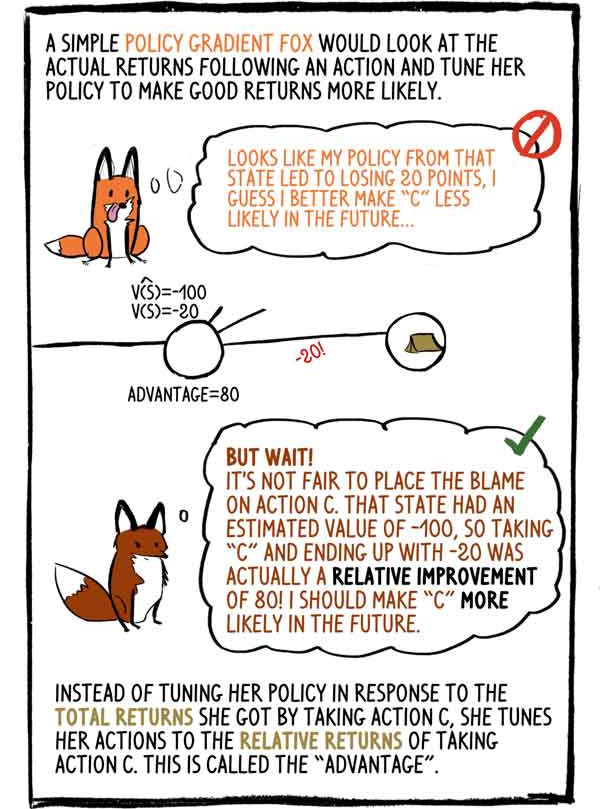
Wir haben darüber gesprochen, wie Klyukovka seinen inneren Kritiker aufstellt. Aber wie verfeinert sie ihr inneres „Thema“? Wie lernt sie, solch exquisite Entscheidungen zu treffen?
Die einfältige Fuchs-Gradienten-Politik würde das tatsächliche Einkommen nach der Aktion untersuchen und ihre Politik anpassen, um ein gutes Einkommen wahrscheinlicher zu machen: - Es scheint, dass meine Politik in diesem Zustand zu einem Verlust von 20 Punkten geführt hat. Ich denke, dass es in Zukunft besser ist, „C“ zu machen. weniger wahrscheinlich.
- Aber warte! Es ist unfair, die Aktion "C" zu beschuldigen. Dieser Zustand hatte einen geschätzten Wert von -100, also war die Wahl von "C" und das Ende mit -20 tatsächlich eine relative Verbesserung von 80! Ich muss "C" in Zukunft wahrscheinlicher machen.
Anstatt seine Richtlinie an die Gesamteinnahmen anzupassen, die sie durch Auswahl von Aktion C erhalten hat, passt sie ihre Aktion an die relativen Einnahmen aus Aktion C an. Dies wird als „Vorteil“ bezeichnet.
Was wir als Vorteil bezeichnet haben, ist einfach ein Fehler. Als Vorteil nutzt Klukovka es, um Aktivitäten, die überraschend gut waren, wahrscheinlicher zu machen. Aus Versehen verwendet sie den gleichen Betrag, um ihren internen Kritiker dazu zu bewegen, ihre Einschätzung des Statuswerts zu verbessern.
Betreff nutzt:
- "Wow, das hat besser funktioniert als ich dachte, Aktion C muss eine gute Idee sein."
Der Kritiker benutzt den Fehler:
„Aber warum war ich überrascht? Ich hätte diesen Zustand wahrscheinlich nicht so negativ bewerten sollen. "
Jetzt können wir zeigen, wie die Gesamtverluste berechnet werden - wir minimieren diese Funktion, um unser Modell zu verbessern.
"Totalverlust = Handlungsverlust + Wertverlust - Entropie"
Bitte beachten Sie, dass wir zur Berechnung der Gradienten von drei qualitativ unterschiedlichen Typen die Werte „bis eins“ verwenden. Dies ist effektiv, kann jedoch die Konvergenz erschweren.

Wie alle Tiere wird Klyukovka mit zunehmendem Alter seine Fähigkeit verbessern, die Werte von Staaten vorherzusagen, mehr Vertrauen in seine Handlungen zu gewinnen und weniger häufig über Auszeichnungen überrascht zu sein.
RL-Agenten wie Klukovka generieren nicht nur alle erforderlichen Daten, sondern interagieren einfach mit der Umgebung, sondern bewerten auch die Zielbezeichnungen selbst. Richtig, RL-Modelle aktualisieren frühere Noten, um sie besser an neue und verbesserte Noten anzupassen.
Wie Dr. David Silver, Leiter der RL-Gruppe bei Google Deepmind, sagt: AI = DL + RL. Wenn ein Agent wie Klyukovka seine eigene Intelligenz einstellen kann, sind die Möglichkeiten endlos ...
