
Hallo habrozhiteli! Dieses Buch basiert auf den Online-Algorithmenkursen, die Tim Rafgarden für Coursera und Stanford Lagunita leitet. Diese Kurse sind dank der Vorlesungen entstanden, die er seit vielen Jahren an Studenten der Stanford University hält.
Algorithmen sind das Herz und die Seele der Informatik. Sie können nicht ohne sie auskommen, sie sind überall - von Netzwerkrouting und Genomikberechnungen bis hin zu Kryptographie und maschinellem Lernen. Der „perfekte Algorithmus“ macht Sie zu einem echten Profi, der Aufgaben festlegt und diese sowohl im Leben als auch bei einem Vorstellungsgespräch meisterhaft löst, wenn Sie ein IT-Unternehmen einstellen. Tim Rafgarden wird über asymptotische Analyse, Big-O-Notation, Divide and Conquer-Algorithmen, Randomisierung, Sortierung und Auswahl sprechen. Das Buch richtet sich an diejenigen, die bereits Programmiererfahrung haben. Sie werden auf eine neue Ebene wechseln, um das Gesamtbild zu sehen und die Konzepte und mathematischen Nuancen auf niedriger Ebene zu verstehen.
* 6.3. DSelect-Algorithmus
Der RSelect-Algorithmus wird für jede Eingabe in linearer Zeit ausgeführt, wobei die mathematische Erwartung mit zufälligen Auswahlmöglichkeiten verbunden ist, die vom Algorithmus ausgeführt werden. Ist für die lineare Auswahl eine Randomisierung erforderlich? In diesem und weiteren Abschnitten wird dieses Problem unter Verwendung eines deterministischen linearen Algorithmus für das Auswahlproblem gelöst.
Für die Sortieraufgabe entspricht die durchschnittliche Laufzeit des randomisierten QuickSort-Algorithmus O (n log n) dem deterministischen MergeSort-Algorithmus, und beide Algorithmen QuickSort und MergeSort sind nützliche Algorithmen für den praktischen Gebrauch. Obwohl der in diesem Abschnitt beschriebene deterministische lineare Auswahlalgorithmus in der Praxis gut funktioniert, konkurriert er nicht mit dem RSelect-Algorithmus. Dies geschieht aus zwei Gründen: aufgrund der großen konstanten Faktoren in der Betriebszeit des DSelect-Algorithmus und der Arbeit des Algorithmus, der mit der Zuweisung und Verwaltung von zusätzlichem RAM verbunden ist. Trotzdem sind die Ideen im Algorithmus so cool, dass ich nicht anders kann, als Ihnen davon zu erzählen.
6.3.1. Geniale Idee: Median der Mediane
Der RSelect-Algorithmus ist schnell, da eine hohe Wahrscheinlichkeit besteht, dass zufällige Unterstützungselemente ziemlich gut sind, was eine annähernd ausgeglichene Aufteilung des Eingabearrays nach der Trennung ermöglicht, und außerdem entwickeln sich ziemlich gute Unterstützungselemente schnell. Wenn wir keine Randomisierung verwenden dürfen, wie können wir dann ein ziemlich gutes Referenzelement berechnen, ohne zu viel Arbeit zu leisten?
Die geniale Idee bei einer deterministischen linearen Wahl besteht darin, den "Median der Mediane" als Proxy für den wahren Median zu verwenden. Der Algorithmus betrachtet Elemente des Eingabearrays als Sportmannschaften und veranstaltet in zwei Runden ein Ko-Turnier, dessen Champion das unterstützende Element ist. siehe auch Abb. 6.1.
Die erste Runde ist eine Gruppenphase mit Elementen an den Positionen 1 bis 5 des Eingabearrays als erste Gruppe, Elementen an den Positionen 6 bis 10 als zweite Gruppe usw. Der Gewinner der ersten Runde einer Gruppe von fünf Elementen wird als der Median des Elements definiert (d. H. Der drittkleinste). Da gibt es
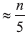
Gruppen von fünf Elementen gibt es
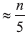
erste Gewinner. (Wie üblich ignorieren wir der Einfachheit halber Brüche.) Ein Turniersieger ist definiert als der Median der Gewinner der ersten Runde.
6.3.2. Pseudocode für DSelect-Algorithmus
Wie berechnet man den Median der Mediane? Die Durchführung der ersten Stufe des Ausscheidungsturniers ist einfach, da jede Berechnung des Medians nur fünf Elemente enthält. Zum Beispiel kann jede solche Berechnung mit roher Gewalt durchgeführt werden (für jede der fünf Möglichkeiten im Detail prüfen, ob es sich um ein mittleres Element handelt) oder anhand unserer Informationen zum Sortierproblem (Abschnitt 6.1.2). Um die zweite Stufe zu implementieren, berechnen wir den Median aus
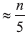
Gewinner der ersten Runde rekursiv.
Die Zeilen 1–2 und 6–13 sind identisch mit dem RSelect-Algorithmus. Die Zeilen 3–5 sind der einzige neue Teil des Algorithmus. Sie berechnen den Median des Medians des Eingabearrays und ersetzen die Linie im RSelect-Algorithmus, der das Referenzelement zufällig auswählt.
Die Zeilen 3 und 4 berechnen die Gewinner der ersten Runde des Ausscheidungsturniers, wobei das mittlere Element jeder Gruppe von fünf Elementen unter Verwendung der Brute-Force-Methode oder des Sortieralgorithmus berechnet wird, und kopieren diese Gewinner in das neue Array C. Zeile 5 berechnet den Champion des Turniers durch rekursive Berechnung des Medians von Array C; da C eine Länge hat (vorläufig)
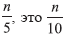
-te Ordnungsstatistik des Arrays C. In keinem Schritt des Algorithmus wird eine Randomisierung verwendet.
6.3.3. Grundlegendes zum DSelect-Algorithmus
Ein rekursiver Aufruf des DSelect-Algorithmus bei der Berechnung eines Referenzelements kann gefährlich zyklisch erscheinen. Um zu verstehen, was los ist, geben wir zunächst die Gesamtzahl der rekursiven Aufrufe an.
Die richtige Antwort lautet: (c). Der DSelect-Algorithmus verwirft den Basisfall und den glücklichen Fall, in dem das Referenzelement die erforderliche Ordnungsstatistik ist, und führt zwei rekursive Aufrufe durch. Um zu verstehen warum, übertreibe es nicht; Überprüfen Sie einfach den Pseudocode des DSelect-Algorithmus Zeile für Zeile. Zeile 5 hat einen rekursiven Aufruf und einen weiteren in Zeile 11 oder 13.
Zu diesen beiden rekursiven Aufrufen gibt es zwei verwirrende häufig gestellte Fragen. Ist es nicht eine Tatsache, dass der RSelect-Algorithmus nur einen rekursiven Aufruf ausführt, der Grund, warum er schneller funktioniert als unsere Sortieralgorithmen? Gibt DSelect diese Verbesserung nicht auf, indem zwei rekursive Aufrufe getätigt werden? Abschnitt 6.4 zeigt, dass wir die lineare Analyse trotzdem speichern können, da der zusätzliche rekursive Aufruf in Zeile 5 nur eine relativ kleine Unteraufgabe lösen sollte (mit 20% der Elemente im ursprünglichen Array).
Zweitens spielen zwei rekursive Aufrufe grundsätzlich unterschiedliche Rollen. Der Zweck des rekursiven Aufrufs in Zeile 5 besteht darin, ein gutes Referenzelement für den aktuellen rekursiven Aufruf zu bestimmen. Das Ziel des rekursiven Aufrufs in Zeile 11 oder 13 ist das übliche - die kleinere verbleibende Aufgabe, die der aktuelle rekursive Aufruf hinterlässt, rekursiv zu lösen. Trotzdem folgt die rekursive Struktur im DSelect-Algorithmus vollständig der Tradition aller anderen von uns untersuchten Divide- und Conquer-Algorithmen: Jeder rekursive Aufruf führt eine kleine Anzahl nachfolgender rekursiver Aufrufe mit streng feineren Unteraufgaben aus und erledigt zusätzliche Arbeit. Wenn wir uns keine Sorgen machen, dass Algorithmen wie MergeSort oder QuickSort für immer ausgeführt werden, sollten wir uns keine Sorgen um den DSelect-Algorithmus machen.
6.3.4. DSelect-Algorithmus-Laufzeit
Der DSelect-Algorithmus ist nicht nur ein klar formuliertes Programm, das in einer begrenzten Zeit abgeschlossen wird. Er wird in linearer Zeit ausgeführt und arbeitet nur mit einem konstanten Faktor mehr, als zum Lesen der Eingabedaten erforderlich ist.
Satz 6.6 (Betriebszeit des DSelect-Algorithmus). Für jedes Eingabearray mit der Länge n ≥ 1 beträgt die Laufzeit des DSelect-Algorithmus O (n).
Im Gegensatz zur Laufzeit des RSelect-Algorithmus, die im Prinzip nicht mehr als Θ (n2) betragen kann, ist die Laufzeit des DSelect-Algorithmus immer gleich O (n). In der Praxis sollten Sie jedoch RSelect dem DSelect-Algorithmus vorziehen, da der erste an derselben Stelle arbeitet und die in Satz 6.1 in der durchschnittlichen Betriebszeit „O (n)“ verborgene Konstante kleiner ist als die in Satz 6.6 verborgene Konstante.
»Weitere Informationen zum Buch finden Sie auf
der Website des Herausgebers»
Inhalt»
AuszugFür Khabrozhiteley 20% Rabatt auf den Gutschein -
AlgorithmenNach Zahlung der Papierversion des Buches wird eine elektronische Version des Buches per E-Mail verschickt.
PS: 7% der Kosten des Buches fließen in die Übersetzung neuer Computerbücher. Die Liste der Bücher, die der Druckerei übergeben wurden, finden Sie
hier .