Myonenkatalyse in Bezug auf die Quantenchemie. Teil I: gewöhnlicher Wasserstoff vs. Myon Wasserstoff

Mnogabukaff, dass die Quantenchemie über das Prinzip der Myonenkatalyse nachdenkt: Wie genau Myon die Temperatur des gewünschten Plasmas senkt. In zwei Teilen.

Die Essenz des ersten Teils wird in einem Satz ausgedrückt: Das Myon ist schwerer als das Elektron, daher ist es schwieriger, es vom Proton abzureißen.

Aber diejenigen, die sich die Formeln und Graphen ansehen und die konzeptionelle Essenz der Quantenchemie auf die einfachsten (quasi) Atome anwenden möchten, sind unter cat willkommen.

Der zweite Teil ist unter diesem Link verfügbar.

Einführung

Es ist kein Geheimnis, dass der Energieverbrauch der Menschheit von Jahr zu Jahr zunimmt: Jeder von uns hat mehr Geräte, wir müssen uns dort bewegen und wir selbst sind nicht weniger. Deshalb denken wir ständig darüber nach, wo wir mehr Energie bekommen und wo wir diese Energie sparen können.

Eine der möglichen Alternativen zu den derzeitigen Hauptenergiequellen (Kohle, Gas, Wasserkraftwerke und Kernkraft) ist die Kernfusion (TS) . Tatsächlich ist dies der gute Zwillingsbruder der bösen Kernenergie, die Hauptsache, an die man sich bei der Zarenbombe nicht erinnern sollte : Anstelle von Fusionsreaktionen in der TS dient die Fusion von leichten Kernen zu schwereren als Energiequelle. Und alles scheint in Ordnung zu sein: Alle unsere Energiequellen sind dank des TS irgendwie erschienen, weil es in den Sternen (einschließlich des Inneren der Sonne) fließt und als Licht- und Wärmequelle dient, wodurch alle Photosynthesereaktionen stattfinden und alle fließen Flüsse und Winde wehen. Aber auch dank TS haben wir eine Reihe von Elementen, die schwerer als Helium sind (einschließlich Kohlenstoff = Kohle, Öl, Gas und Uran).
Die wichtigsten mutmaßlichen Synthesereaktionen sind die Fusionsreaktionen verschiedener Wasserstoffisotope (Protium) $$${} _ {1} ^ {1} \ mathrm {H}$ Deuterium $$${} _ {1} ^ {2} \ mathrm {H}$ und Tritium $$${} _ {1} ^ {3} \ mathrm {H}$ )

Das Problem ist, dass Sie unglaublich hohe Temperaturen benötigen, um das Fahrzeug in einem autarken Modus zu starten. Es gibt kein Problem mit den Sternen, aber unter terrestrischen Bedingungen ist eine solche Anforderung immer noch ein Hindernis für den Strom, der aus einer umweltfreundlichen Kernfusion in jedem Auslass fließt.

Eine Möglichkeit, die Temperatur zu senken, ist die Myonenkatalyse .
Vicki sagt uns, dass Myon ( $$$\ mu ^ -$ ) Ist so ein instabiler schwerer Elektronenklon ( $$$e ^ -$ ): Es ist 207-mal schwerer als ein Elektron und lebt nur 2,2 Mikrosekunden. Es wird jedoch angenommen, dass die Zugabe solcher Partikel zu dem System, in dem der TS auftritt, die minimale Plasmatemperatur senken kann, die für die Fusion neuer Kerne erforderlich ist. Und da sich während einiger Synthesereaktionen Myonen bilden können, anstatt neue Partikel zu zerfallen, sollten neue Partikel erscheinen, die weiterhin Alchemie betreiben, um Wasserstoff und andere Elemente unter Bildung schwererer zu verbrennen.

In den Unterschieden zwischen den üblichen Formen von Wasserstoff und denen, bei denen das Elektron durch ein Myon ersetzt wird, liegt die gesamte Essenz der Myonkatalyse. Und um dies zu sehen, müssen wir uns der Quantenchemie und ihren Konzepten zuwenden, was wir tun werden.

In diesem Teil konzentrieren wir uns auf Unterschiede im Wasserstoffatom ( $$$\ mathrm {H ^ \ cdot = p ^ + e ^ -}$ ) von seinem Myon-Gegenstück ( $$$\ mathrm {p} ^ + \ mu ^ -$ ), bei dem das Elektron durch ein Myon ersetzt wird.

Über das Nest des Protons fliegen ...

Ein paar gebräuchliche Wörter

Wasserstoffatom. Alle diskutieren darüber und finden in der Schule im Physik- und Chemieunterricht statt. Wir werden daher diskutieren, wie sich das Ersetzen eines Elektrons durch ein Myon auf seine Eigenschaften (Energie und Art der Orbitale) auswirkt.
Wir betrachten diese Teilchen aus zwei allgemeinen Positionen:

• pervers (die sogenannte alte Quantenmechanik),
• und aus Sicht des normalen Quantenmech.

Die erste Überlegung steht Schulkindern zur Verfügung, die zweite erfordert tiefere Kenntnisse der höheren Mathematik .

Bohr umkreist

Tatsächlich ist die alte Quantenmechanik ein Versuch, die klassische Mechanik anzupassen, um Systeme zu beschreiben, die ihr nicht gehorchen. Trotz der Tatsache, dass dieser Ansatz für eine vollständige Beschreibung sehr fehlerhaft ist (was wir im nächsten Abschnitt diskutieren werden), ist er wichtig und interessant und gleichzeitig ungewöhnlich einfach.

• Erstens gelang es den Physikern durch die alte Quantenmechanik herauszufinden, was mit Quantensystemen nicht stimmte. Aus historischer Sicht war dieser Schritt daher notwendig und wichtig, um das Paradigma der Physik zu ändern.
• Zweitens könnte Bohrs Lösung für das Problem eines Atoms wasserstoffähnlicher Atome, das aus zwei positiv und negativ geladenen Teilchen besteht, die experimentellen Beobachtungen erklären und den gesamten beobachteten Reihenzoo in den Wasserstoffspektren miteinander verbinden. Eine schädliche Version dieser Entscheidung, die Bohr den Nobelpreis 1922 brachte, werden wir hier betrachten.

Um das Problem zu lösen, müssen wir uns daran erinnern, wie wir die Bewegung eines Teilchens im klassischen Fall beschreiben. Dies ist ein Schulprogramm in Physik, aber wenn jemand es vergessen hat, können Sie Ihr Gedächtnis hier auffrischen:




Fahren wir mit der Aufgabe fort. Wir haben also zwei entgegengesetzt geladene Teilchen, die gemäß dem Coulomb-Gesetz voneinander angezogen werden, d.h. potentielle Energie der Anziehung ist

$$

$$V (R) = \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1 q_2} {R}$$

wobei R der Abstand zwischen den Partikeln ist, $$$q_i$ - Ladungen bei einem Wasserstoffatom und einem Partikel $$$\ mathrm {p} ^ + \ mu ^ -$ Sie sind gleich $$$+ e \ ca. +1,6 \ mal 10 ^ {- 19}$ CL für Proton und $$$-e$ für Elektron und Myon und $\ varepsilon_0$ - elektrische Konstante . Da die Ladungen entgegengesetzt sind, nimmt die potentielle Energie mit abnehmendem Abstand zwischen den Teilchen ab (d. H. Während der Annäherung), was bedeutet, dass das Proton und das Elektron / Myon voneinander angezogen werden.

Diese Situation ist im obigen Bild dargestellt. Aber irgendwo haben wir ein ähnliches System gesehen, oder? Tatsächlich leben wir auf einem dieser Paare: Sonne + Erde oder Erde + Mond oder Erde + ISS - dies sind auch zwei Teilchen, die von einem ähnlichen Potential angezogen werden, das durch das Newtonsche Gesetz ausgedrückt wird:

$$

$$V (R) = -G \ frac {m_1 m_2} {R}$$

wobei G die Gravitationskonstante ist und $$$m_i$ - Massen.

Das Proton ist 1836-mal schwerer als das Elektron, und da das Myon 207-mal schwerer als das Elektron ist, ist das Proton fast 9-mal schwerer als das Myon. In beiden Fällen haben wir das System „Schweres Teilchen + Leichtes Teilchen“, also nehmen wir die Näherung, in der sich das Elektron / Myon um ein Proton dreht. Natürlich ist die Richtigkeit dieser Annahme im Fall von $$$\ mathrm {p} ^ + \ mu ^ -$ wird deutlich niedriger sein als für ein Wasserstoffatom, aber zur Veranschaulichung ist es ziemlich geeignet. In den Fällen von Sonne + Erde verwendet Erde + ISS normalerweise ähnliche Näherungen.

Wir sind an einem stabilen System interessiert, in das nirgendwo etwas fällt, weil Wasserstoffatome existieren, wenn sie unberührt bleiben, sehr lange.

Wir kennen solche Bewegungen bei allen Analoga aus dem Sonnensystem, sind aber für das Paar Erde + ISS sogar offensichtlich: Dies sind stabile Umlaufbahnen, bei denen sich die Station mit einer Geschwindigkeit um die Erde bewegt, die ausreicht, um nicht zu fallen. Diese Geschwindigkeit wird die erste kosmische Geschwindigkeit genannt , d.h. Wir würden die erste kosmische Geschwindigkeit für das Wasserstoffatom / sein Myon-Gegenstück benötigen. Und es ist leicht, es anhand von Schulformeln zu finden (siehe Abbildung oben).

Bei Bewegung in einer Kreisbahn mit Radius R (in der Abbildung ist dies als angegeben $$$a_0$ und bald kommen wir dazu) Sie müssen Geschwindigkeit haben $$$v$ . Man kann sich vorstellen, dass in jedem Moment zwei Kräfte, die auf ein in einem Kreis fliegendes Teilchen wirken, senkrecht zum Geschwindigkeitsvektor sind:

• Coulomb-Schwerkraft auf das Zentrum gerichtet, die nach der Definition der Kraft $$$F = - \ frac {dV} {dR}$ ist gleich
  

  $$

  $$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$$
  
  
• Die (falsche) Zentrifugalkraft, die versucht, den Radius der Umlaufbahn R zu vergrößern, wirkt ihr entgegen. Der Ausdruck dafür hat die Form
  

  $$

  $$F_ \ text {q} = \ frac {mv ^ 2} {R}$$
  
  Dabei ist m die Masse des Elektrons / Myons (des natürlichen Satelliten des Protons).
  

Die Bedingung, dass ein leichtes Teilchen nicht gegen ein schweres stößt, ist, dass die Summe dieser Kräfte senkrecht zur Bewegungsrichtung des Teilchens Null sein sollte ( $$$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ), was bedeutet, dass wir die Gleichung erhalten

$$

$$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$$

woher bekommen wir die Geschwindigkeit, mit der es notwendig ist, ein Elektron / Myon mit der Masse m im Radius der Umlaufbahn R zu fliegen, um nicht auf das Proton zu stoßen:

$$

$${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$$

Und alles wäre verletzt, wenn das Elektron / Myon nicht geladen wäre und geladene Teilchen elektromagnetische Wellen aussenden, wenn sie sich in einem Kreis bewegen (dies wird als Strahlungsreibung bezeichnet) , was ein solches System instabil machen würde: Das Elektron / Myon würde während der Rotation Licht emittieren. Infolgedessen verlor es Energie und verringerte den Radius seiner Umlaufbahn, und schließlich würde es auf ein Proton fallen, und alles würde ein kleines weißes, flauschiges Tier enthalten . Dies geschieht jedoch offensichtlich nicht, was bedeutet, dass sich etwas im Verhalten so kleiner Teilchen wie des Elektrons / Myons radikal unterscheiden sollte.

Tatsächlich schlug Niels Bohr auch eine (damals) sehr dumme Hypothese vor. Er gab zu, dass es Bahnen mit einem bestimmten Radius gibt, auf denen das Wasserstoffatom nichts emittiert. Und jetzt ist die Frage, wie man diese Umlaufbahnen findet. Der Einfachheit halber werden wir die Errungenschaft später verwenden, als Bohr zur Verfügung stand: der Ausdruck für die Wellenlänge von de Broglie :

$$

$$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$$

Es wird angenommen, dass Materie (Teilchen) auch Welleneigenschaften haben, und ihnen kann eine bestimmte Wellenlänge zugeordnet werden, die durch die de Broglie-Formel gegeben ist. Damit die Bewegung in einem Kreis zeitlich stationär ist (eine stehende Welle), ist es erforderlich, dass die Länge der Umlaufbahn ( $$$L = 2 \ pi R$ ) eine ganzzahlige Anzahl von Wellen anpassen.

Dann kann die Wellenbewegung des Elektrons / Myons irgendwie so dargestellt werden ( aus dem Wiki ):

In der Sprache der Formeln wird dies ausgedrückt als:

$$

$$2 \ pi R = n \ lambda = n \ frac {h} {mv}$$

Wenn wir hier die erste kosmische Protonengeschwindigkeit einsetzen, die oben erhalten wurde, erhalten wir die Gleichung $$$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ . Nachdem wir beide Seiten quadriert haben, erhalten wir den Ausdruck für den Radius der n-ten stationären Elektronen / Myon-Umlaufbahn:

$$

$$R_n = n ^ 2 \ left (\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ right) ^ 2 \ cdot \ frac {1} {mk e ^ 2} = \ frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$$

Hier $$$n = 1,2,3, \ ldots$ (Wir haben keine Begrenzung für die Anzahl der zu verlegenden Wellen) und $$$\ hbar$ - das ist das sogenannte reduzierte Planck-Konstante. Je mehr Wellen wir stapeln, desto größer ist der Radius der Umlaufbahn. Mit dem minimalen Radius ( n = 1) im Fall eines Elektrons (d. H. M ist gleich der Masse des Elektrons m _e ) wird dieser Radius, wie K.O. zu Ehren von Niels Bohr sagt, als Bohr-Radius bezeichnet und als _{0 bezeichnet} (siehe Abb. Oben):

$$

$$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$$

Die Substitution von Zahlen ( ħ = 1,054 × 10 ^–34 J · s, m _e = 9,109 × 10 ^–31 kg, k = 8,99 × 10 ⁹ N · m ² · C ^–2 und e = –1,602 × 10 ^–19 C) ergibt der Wert a ₀ = 5,29 × 10 ^–11 m oder 0,529 Angström (Å).


Im Verlauf der Berechnungen haben wir nebenbei eine neue Entität eingeführt: die Zahl $$$n = 1,2,3, \ ldots$ welches die Anzahl der Wellen bestimmt und $$$\ Rightarrow$ der Radius der Umlaufbahn und sogar die Geschwindigkeit des Elektrons in der Umlaufbahn. Diese Zahl ist jedem aus der Schule bekannt: Dies ist die wichtigste Quantenzahl eines wasserstoffähnlichen Atoms. Wir werden im nächsten Abschnitt ausführlicher darauf eingehen, aber jetzt können Sie versuchen, die Energie der einzelnen Ebenen zu ermitteln.

Nach unserem Verständnis besteht die Energie eines geschlossenen Systems (und es besteht kein Zweifel daran, dass unser wasserstoffähnliches Atom so ist) aus zwei Teilen:

• aus kinetischer Energie $$$T = \ frac {mv ^ 2} {2}$ ,
• und Potenzial, das in unserem Fall durch das Gesetz von Coulomb gegeben ist $$$V = \ frac {ke ^ 2} {R}$ .

Wir ersetzen die gewählte Hauptzahl n durch die Geschwindigkeit und den Radius der Umlaufbahn. Wir haben den Radius bereits ausgeschrieben, aber die Geschwindigkeit wird so aussehen $$$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ .

Dann $$$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ . Mit Potenzial ist alles einfacher: $$$V_n = - \ frac {ke ^ 2} {R_n} = - \ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ . Zusammenfassend erhalten wir die Gesamtenergie eines wasserstoffähnlichen Atoms:

$$

$$E_n = T_n + V_n = - \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$$

Und diese Formel spielte eine große Rolle beim Nachweis der Richtigkeit der Quantenmechanik, da in den Spektren des Wasserstoffatoms Haufen von Spektrallinien (Lyman, Balmer, Paschen usw.) beobachtet wurden. Und mit einer Formel und einem einfachen Modell konnten sie alle auf einmal erklärt werden, was ein erstaunlich überzeugendes Argument für die Anerkennung von Bohrs Ideen war.

Nachdem wir alle Säfte aus diesem einfachsten Modell herausgepresst haben, können wir vom Standpunkt der ehrlichen Quantenmechanik zur richtigen Betrachtung des Problems übergehen.

Orbitale eines wasserstoffähnlichen Atoms

Das zweite, noch wichtigere ist, was Quantenmechanik ist und wie sie funktioniert. Dies kann aus verschiedenen Quellen in Erinnerung bleiben. Ich empfehle:

• nicht weit gehen, ein Artikel von Habr: Buch „Quantenmechanik. Theoretisches Minimum “ (ein Stück des gleichnamigen Buches von Leonard Sasskind und Art Friedman ),
• tolles Buch "Wie man Quantenmechanik versteht" von MFTIshnogo Lehrer MG Ivanova (zum Download über den Link verfügbar),
• Im dxdy-Forum in den Auserwählten gibt es viele Beiträge, die die Essenz des Quanten gut erklären.
• durchaus passender Rückblick und historischer Artikel über Lurke ,
• Nun, der gesamte Müll ist auch im Internet zu finden.

  Netzwerkhandbuch zur Quantenchemie von VK .
  

Es gibt hier jedoch auch einen Hardcore-Druck auf die notwendigen Dinge:


Um herauszufinden, wie sich ein Elektron / Myon in einem von einem Proton erzeugten elektrischen Coulomb-Feld bewegt, muss man die Grundgleichung der Quantenmechanik lösen: die Schrödinger-Gleichung. Da das betrachtete System stationär ist (sich im Laufe der Zeit nicht ändert), reicht es aus, seine vereinfachte Version zu lösen: die stationäre Schrödinger-Gleichung, die die Form hat

$$

$$\ underbrace {(\ overbrace {- \ frac {\ hbar ^ 2} {2m} \ cdot \ left (\ frac {\ partielle ^ 2} {\ partielle x ^ 2} + \ frac {\ partielle ^ 2} { \ partielle y ^ 2} + \ frac {\ partielle ^ 2} {\ partielle z ^ 2} \ rechts)} ^ {\ hat {T}} + \ overbrace {- \ frac {ke ^ 2} {R}} ^ {\ hat {V}})} _ {\ hat {H}} \ psi = E \ psi$$

Diese Gleichung ist eine partielle Differentialgleichung zweiter Ordnung, in der wir gleichzeitig nach der Wellenfunktion suchen $$$\ psi (x, y, z)$ Beschreibung des spezifischen Zustands des Systems und Darstellung des "Verschmierens" des negativen Teilchens im Raum um das Proton und der Energie dieses Zustands E. Hexerei, die darüber entscheidet, ist mehr oder weniger überall zu finden .


Aber eine einfachere Sache: Jeder, der mit Differentialgleichungen vertraut ist, kann eine Lösung für den Grundzustand eines wasserstoffähnlichen Atoms finden. Um nicht alle anderen zu erschrecken, wird dieses Teil im Spoiler entfernt:


Das Ergebnis der Lösung der Schrödinger-Gleichung ist eine Menge von Orbitalen, die unter Verwendung von drei ganzen Zahlen n , l und m beschrieben werden , die als "Quantenzahlen" bezeichnet werden. Die Abhängigkeit der Energien dieser Orbitale von $$$(n, l, m)$ unten angegeben (und steren von einer coolen Ressource in der Chemie ):

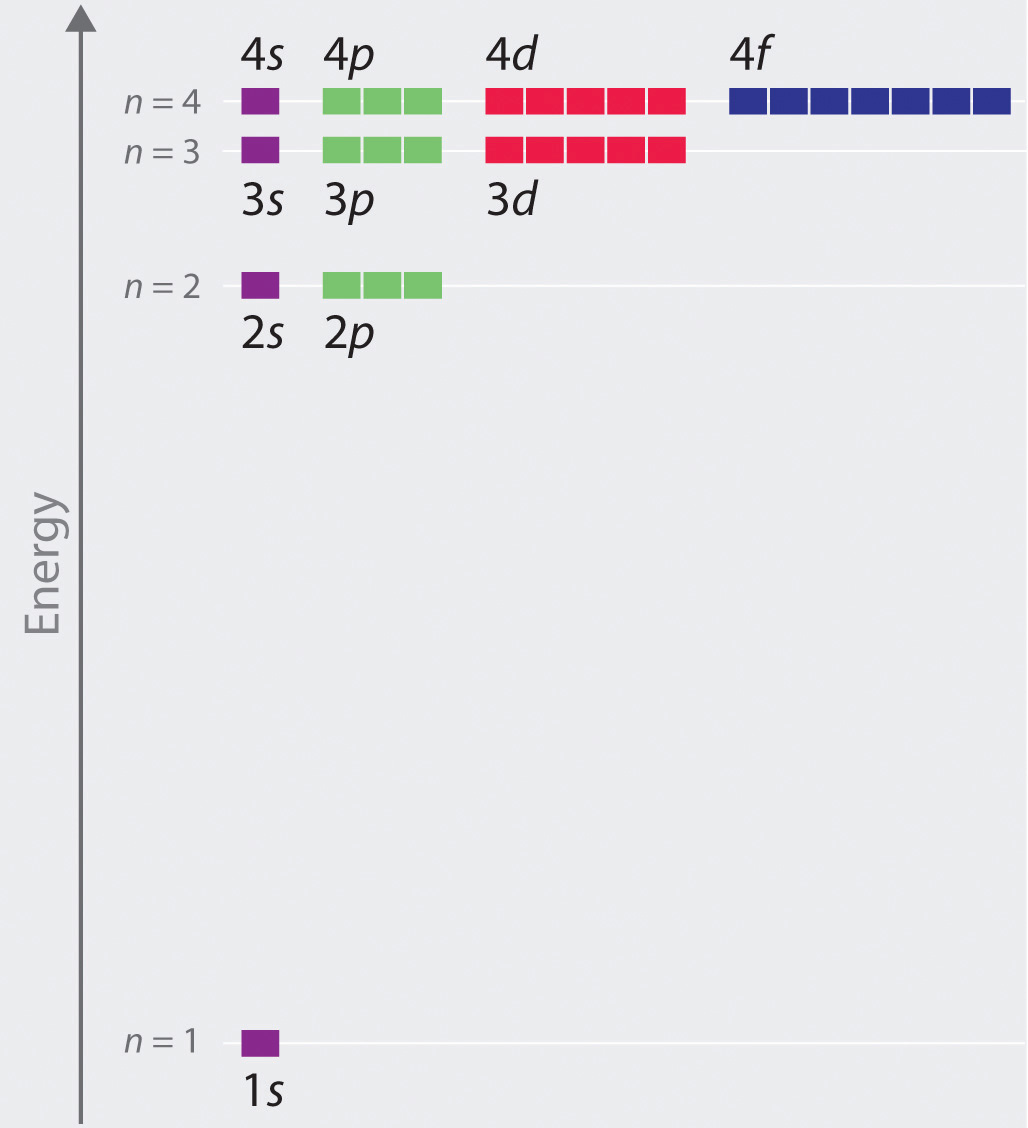
1. Mit der ersten Zahl, n = 1,2,3, ... haben wir uns bereits getroffen. Dies ist das sogenannte Hauptquantenzahl. Es bestimmt die Energie des Levels sowie die Größe der Bohr-Umlaufbahn. (.. ) «». , / , , — , , , . n =1 n =2 ( ):
   
   
   : , n . , .
2. l , , . n , n ( $$$l = 0, 1,2, \ldots, n$ ) , . , , . , ( $$$\psi=0$ ), , . - ( ):
   
   
   
   «» . , .
   
   
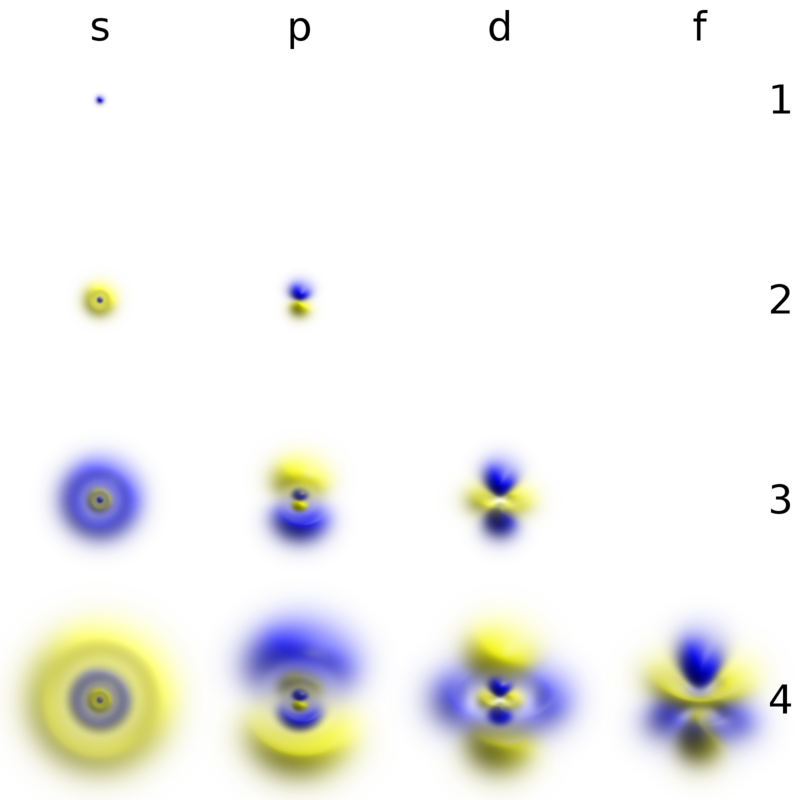
   • $$$l=0$ , , , . s-.
   • ( $$$l=1$ ) p-.
   • 4- $$$l=2$ , d-. .
   • 6- ( $$$l=3$ ) f-.
   • 8- ( $$$l=4$ ) g-.
   • 10- ( $$$l=5$ ) h-.
   • Usw. usw.
   
   , ( n ) , . : , .
   
3. , m , . . 2l+1 : $$$m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$ .

Was wir als Ergebnis erhalten haben: Die Energien im Quantenfall erwiesen sich als die gleichen wie die von Bohr, aber die Anzahl der möglichen Zustände für ein gegebenes n erwies sich auch als endliche Zahl. Und diese Zahl wächst mit zunehmender Orbitalenergie. Unerwartet, aber in guter Übereinstimmung mit Experimenten.

Was ist also der Unterschied zwischen einem Wasserstoffatom ( $$H ⋅ = p + e - ) von seinem Myon-Gegenstück ($\mathrm{H}^\cdot = \mathrm{p^+ e^-}$$$$\mathrm{p}^+ \mu^-$ )?

Nun wenden wir die erhaltenen Formeln an, um zu verstehen, was sich genau ändert, wenn ein Elektron in einem Wasserstoffatom durch ein Myon ersetzt wird.

• Die Energie des Grundzustands (d. H. Das Minimum an Energie, das stabilste, von wo aus man nirgendwo hingehen kann) mit der Hauptquantenzahl n = 1. Es ist durch die Formel gegeben
  

  $$

  $$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$$
  
  ( $$$m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $$$E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
  
• . //, . $$$\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $$$\mathrm{A \rightarrow A^+ + \mu^-}$ . . $$$E=0$ . $$$E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ bei $$$n \rightarrow + \infty$ . Das heißt, , , / , , - (. ).
  
  , ( $$$E>0$ , ).
  
  , (IP) +/ :
  

  $$

  $$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$$
  
  , + 207 , , .. «» , .
  
• , «». , , (1s-)
  

  $$

  $$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$$
  
  $$$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ je schneller die Wellenfunktion mit dem Abstand vom Proton abnimmt und je kleiner seine "Größe" ist, d.h. Lokalisierung eines negativ geladenen Teilchens. Beim Übergang von einem Elektron zu einem Myon nimmt dieser Radius R ₁ um den Faktor 207 ab, daher stellt sich heraus, dass das Myon enger an das Proton gebunden ist als das Elektron. Und deshalb ist es schwieriger, es abzureißen, da die Ionisation im Wesentlichen ein Übergang zu einer unendlich entfernten Umlaufbahn ist, d.h. Das Myon muss mehr als das Elektron gehen, um aus dem Proton zu entkommen.
  

Konzeptionell sind alle unsere Schlussfolgerungen aus den Formeln unendlich einfach: das Problem zu lösen für $$$\ mathrm {H ^ \ cdot}$ und $$$\ mathrm {p} ^ + \ mu ^ -$ Sie sehen genauso aus, aber aufgrund der Tatsache, dass das Myon schwerer ist, haftet es mehr am Proton und es ist schwieriger für ihn, ihm zu entkommen.

Offensichtlich richtig? Aber mit den Formeln ist es noch offensichtlicher.

Was wird als nächstes passieren?

Dieser Text war nur eine Vorbereitung für den nächsten Teil.

Darin werden wir den vorgeschlagenen Mechanismus zur Absenkung der minimalen Schmelztemperatur direkt diskutieren.

PS-Atomsystem von Einheiten

Schließlich diskutieren wir eine Sache, die uns alle oben geschriebenen Formeln erheblich vereinfachen würde. Bei verschiedenen (sogar schulischen) Aufgaben kann die Wahl der Maßeinheiten das Leben erheblich erleichtern. Und im Fall der Quantenmechanik gibt es auch ein sehr praktisches Einheitensystem. Dies ist das sogenannte atomares Einheitensystem . Es gehört zur Klasse der natürlichen Einheiten, die im Wesentlichen das Gegenteil von anthropozentrischen Einheiten ( SI , GHS ) ist, in denen Mengen, die sich eine Person sofort vorstellen kann, als Referenzstücke verwendet werden. Zum Beispiel ist in SI die Längeneinheit ein Meter (ungefähr die Länge eines Armes / Beines eines Erwachsenen), die Masse - ein Kilogramm (ungefähr die Masse des Bieres in einem Kreis auf dem Oktoberfest), all dies beobachten wir im täglichen Leben.

Natürliche Einheitensysteme basieren jedoch auf etwas, das Formeln im entsprechenden Wissensbereich vereinfacht. Und bei atomaren Einheiten:

• Zunächst wird angenommen, dass die allgegenwärtige Planck-Konstante Einheit ist ( $$$\ hbar = 1$ ),
• Masseneinheit ist die Masse des Elektrons $$$m_ \ mathrm {e} \ ca. 9,1 \ mal 10 ^ {- 31}$ kg
• Die Ladungseinheit ist die Protonenladung (oder äquivalent der Elektronenladungsmodul). $$$e = 1,6 \ mal 10 ^ {- 19}$ Kl
• Nun, gleichzeitig wird die elektrische Konstante als Einheit genommen $$$k = \ frac {1} {4 \ pi \ varepsilon_0}$ , aufgrund dessen das Gesetz von Coulomb die Form annimmt $$$V (R) = \ frac {q_1 q_2} {R}$ .

In diesem Fall wird der Bohr-Radius des Grundzustands für das Wasserstoffatom zur Längeneinheit $$$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ (Wie wir uns erinnern, sind dies ungefähr 0,5 Å). Die Energieeinheit wird zu einem Wert namens Hartree (zu Ehren des D- Winkels von Hartree ), der bezeichnet wird $$$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ . Es ist ersichtlich, dass die Energie des 1s-Wasserstoffniveaus in atomaren Einheiten 0,5 Hartree beträgt.

Im nächsten Teil werden wir aktiv in diesen Einheiten sitzen.