Hallo Habr! Ich mache Sie auf eine Übersetzung des Artikels
"Q-Learning verstehen, das Cliff Walking-Problem" von
Lucas Vazquez aufmerksam .
Im letzten Beitrag haben wir das Problem „Auf einem Felsen gehen“ vorgestellt und uns für einen schrecklichen Algorithmus entschieden, der keinen Sinn ergab. Dieses Mal werden wir die Geheimnisse dieser grauen Box enthüllen und sehen, dass sie überhaupt nicht so beängstigend ist.
Zusammenfassung
Wir sind zu dem Schluss gekommen, dass wir durch die Maximierung der Anzahl zukünftiger Belohnungen auch den schnellsten Weg zum Ziel finden. Unser Ziel ist es nun, einen Weg zu finden, dies zu tun!
Einführung in Q-Learning
- Beginnen wir mit der Erstellung einer Tabelle, die misst, wie gut eine bestimmte Aktion in einem beliebigen Zustand ausgeführt wird (wir können sie mit einem einfachen Skalarwert messen. Je größer der Wert, desto besser die Aktion).
- Diese Tabelle enthält eine Zeile für jeden Status und eine Spalte für jede Aktion. In unserer Welt hat das Raster 48 Zustände (4 mal Y mal 12 mal X) und 4 Aktionen sind zulässig (oben, unten, links, rechts), sodass die Tabelle 48 x 4 ist.
- Die in dieser Tabelle gespeicherten Werte werden als "Q-Werte" bezeichnet.
- Dies sind Schätzungen der Höhe zukünftiger Belohnungen. Mit anderen Worten, sie schätzen, wie viel mehr Belohnungen wir vor dem Ende des Spiels erhalten können, wenn wir uns in Zustand S befinden und Aktion A ausführen.
- Wir initialisieren die Tabelle mit zufälligen Werten (oder einer Konstanten, zum Beispiel allen Nullen).
Die optimale „Q-Tabelle“ hat Werte, die es uns ermöglichen, in jedem Zustand die besten Maßnahmen zu ergreifen, um am Ende den besten Weg zu finden, um zu gewinnen. Das Problem ist gelöst, Prost, Robot Lords :).
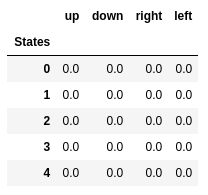Q-Werte der ersten fünf Zustände.Q-Learning
- Q-Learning ist ein Algorithmus, der diese Werte „lernt“.
- Mit jedem Schritt erhalten wir mehr Informationen über die Welt.
- Diese Informationen werden verwendet, um die Werte in der Tabelle zu aktualisieren.
Nehmen wir zum Beispiel an, wir sind einen Schritt vom Ziel entfernt (Quadrat [2, 11]), und wenn wir uns entscheiden, nach unten zu gehen, erhalten wir eine Belohnung von 0 anstelle von -1.
Wir können diese Informationen verwenden, um den Wert des Status-Aktions-Paares in unserer Tabelle zu aktualisieren. Wenn wir es das nächste Mal besuchen, wissen wir bereits, dass wir nach unten eine Belohnung von 0 erhalten.
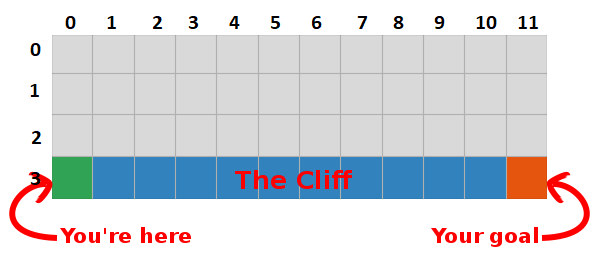
Jetzt können wir diese Informationen noch weiter verbreiten! Da wir jetzt den Weg zum Ziel vom Quadrat aus kennen [2, 11], ist auch jede Aktion, die uns zum Quadrat führt [2, 11], gut. Deshalb aktualisieren wir den Q-Wert des Quadrats, der uns zu [2, 11] führt. näher an 0 sein.
Und das, meine Damen und Herren, ist die Essenz des Q-Lernens!
Bitte beachten Sie, dass wir jedes Mal, wenn wir das Ziel erreichen, unsere „Karte“ zum Erreichen des Ziels um ein Quadrat erhöhen. Nach einer ausreichenden Anzahl von Iterationen erhalten wir eine vollständige Karte, die uns zeigt, wie wir aus jedem Zustand zum Ziel gelangen.
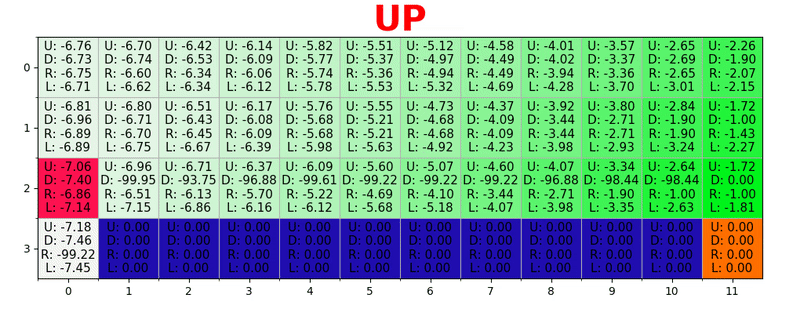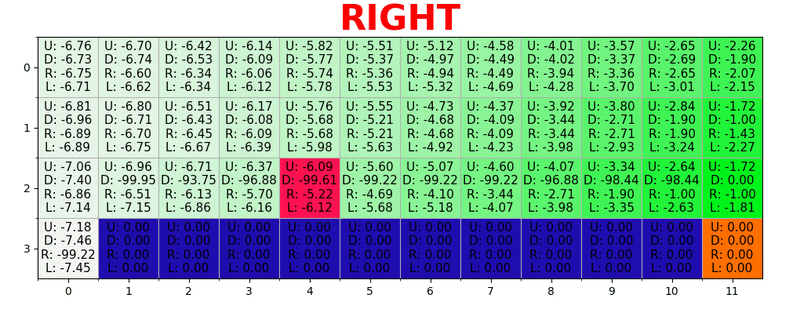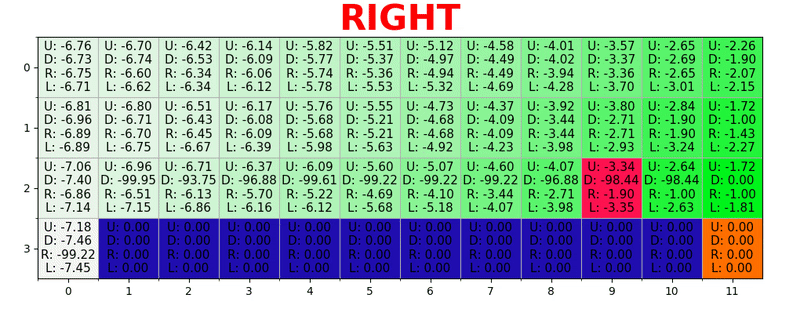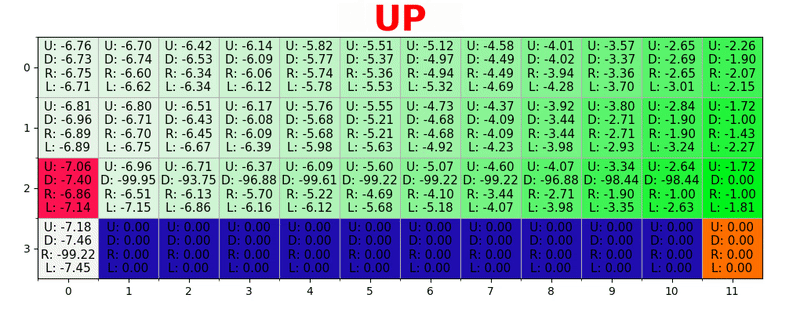Ein Pfad wird generiert, indem in jedem Zustand die beste Aktion ausgeführt wird. Die grüne Taste steht für die Bedeutung einer besseren Aktion, die gesättigten Tasten für einen höheren Wert. Der Text stellt einen Wert für jede Aktion dar (nach oben, unten, rechts, links).Bellman-Gleichung
Bevor wir über Code sprechen, sprechen wir über Mathematik: das Grundkonzept des Q-Lernens, die Bellman-Gleichung.
- Vergessen wir zuerst γ in dieser Gleichung
- Die Gleichung besagt, dass der Q-Wert für ein bestimmtes Zustands-Aktions-Paar die Belohnung sein sollte, die beim Übergang in einen neuen Zustand (durch Ausführen dieser Aktion) erhalten wird, addiert zum Wert der besten Aktion im nächsten Zustand.
Mit anderen Worten, wir verbreiten Schritt für Schritt Informationen über die Werte von Aktionen!
Wir können jedoch entscheiden, dass der Erhalt einer Belohnung im Moment wertvoller ist als der Erhalt einer Belohnung in der Zukunft. Daher haben wir γ, eine Zahl von 0 bis 1 (normalerweise von 0,9 bis 0,99), die in Zukunft mit einer Belohnung multipliziert wird. zukünftige Belohnungen rabattieren.
Wenn also γ = 0,9 gegeben ist und dies auf einige Zustände unserer Welt (Gitter) angewendet wird, haben wir:
Wir können diese Werte mit den oben genannten in GIF vergleichen und feststellen, dass sie gleich sind.
Implementierung
Nachdem wir ein intuitives Verständnis der Funktionsweise von Q-Learning haben, können wir über die Implementierung all dessen nachdenken und den Q-Learning-Pseudocode aus Suttons Buch als Leitfaden verwenden.
Pseudocode aus Suttons Buch.Code:
- Zunächst sagen wir: „Für alle Zustände und Aktionen initialisieren wir Q (s, a) willkürlich“. Dies bedeutet, dass wir unsere Tabelle mit Q-Werten mit beliebigen Werten erstellen können. Sie können zufällig sein, sie können es spielt keine Rolle, dauerhaft zu sein. Wir sehen, dass wir in Zeile 2 eine Tabelle voller Nullen erstellen.
Wir sagen auch: "Der Wert von Q für die Endzustände ist Null", wir können in den Endzuständen keine Aktion ausführen, daher betrachten wir den Wert für alle Aktionen in diesem Zustand als Null.
- Für jede Episode müssen wir "S initialisieren". Dies ist nur eine ausgefallene Art, "Spiel neu starten" zu sagen. In unserem Fall bedeutet dies, den Spieler in die Ausgangsposition zu bringen. In unserer Welt gibt es eine Methode, die genau das tut, und wir nennen sie in Zeile 6.
- Für jeden Zeitschritt (jedes Mal, wenn wir handeln müssen) müssen wir die aus Q erhaltene Aktion auswählen.
Denken Sie daran, ich sagte: „Ergreifen wir die Maßnahmen, die unter allen Bedingungen am wertvollsten sind?
Wenn wir dies tun, verwenden wir unsere Q-Werte, um die Richtlinie zu erstellen. In diesem Fall wird es eine gierige Politik sein, weil wir immer Maßnahmen ergreifen, die unserer Meinung nach in jedem Staat am besten sind. Deshalb wird gesagt, dass wir gierig handeln.
Junk
Bei diesem Ansatz gibt es jedoch ein Problem: Stellen Sie sich vor, wir befinden uns in einem Labyrinth mit zwei Belohnungen, von denen eine +1 und die andere +100 beträgt (und jedes Mal, wenn wir eine davon finden, endet das Spiel). Da wir immer Maßnahmen ergreifen, die wir als die besten betrachten, bleiben wir bei der ersten gefundenen Auszeichnung hängen und kehren immer wieder zu dieser zurück. Wenn wir also zuerst die + 1-Auszeichnung anerkennen, werden wir die große + 100-Auszeichnung verpassen.
Lösung
Wir müssen sicherstellen, dass wir unsere Welt ausreichend studiert haben (dies ist eine erstaunlich schwierige Aufgabe). Hier kommt ε ins Spiel. ε im gierigen Algorithmus bedeutet, dass wir eifrig handeln müssen, ABER zufällige Aktionen als Prozentsatz von ε im Laufe der Zeit ausführen. Bei einer unendlichen Anzahl von Versuchen müssen wir also alle Zustände untersuchen.
Die Aktion wird gemäß dieser Strategie in Zeile 12 mit epsilon = 0,1 ausgewählt, was bedeutet, dass wir 10% der Zeit auf der Welt forschen. Die Umsetzung der Richtlinie erfolgt wie folgt:
def egreedy_policy(q_values, state, epsilon=0.1):
In Zeile 14 in der ersten Liste nennen wir die Schrittmethode, um die Aktion auszuführen. Die Welt gibt uns den nächsten Status, die Belohnung und Informationen über das Ende des Spiels zurück.
Zurück zur Mathematik:
Wir haben eine lange Gleichung, lassen Sie uns darüber nachdenken:
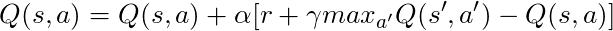
Wenn wir α = 1 nehmen:
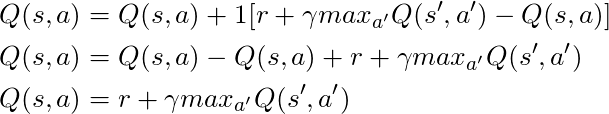
Was genau der Bellman-Gleichung entspricht, die wir vor einigen Absätzen gesehen haben! Wir wissen also bereits, dass dies die Leitung ist, die für die Verbreitung von Informationen über Zustandswerte verantwortlich ist.
Aber normalerweise ist α (meistens als Lerngeschwindigkeit bekannt) viel kleiner als 1, sein Hauptziel ist es, große Änderungen in einem Update zu vermeiden. Anstatt ins Ziel zu fliegen, nähern wir uns ihm langsam. In unserem tabellarischen Ansatz verursacht das Setzen von α = 1 keine Probleme, aber bei der Arbeit mit neuronalen Netzen (mehr dazu in den folgenden Artikeln) kann alles leicht außer Kontrolle geraten.
Wenn wir uns den Code ansehen, sehen wir, dass in Zeile 16 in der ersten Auflistung, die wir td_target definiert haben, dies der Wert ist, dem wir näher kommen sollten, aber anstatt direkt zu diesem Wert in Zeile 17 zu gehen, berechnen wir td_error und verwenden diesen Wert in Kombination mit der Geschwindigkeit lernen, sich langsam dem Ziel zu nähern.
Denken Sie daran, dass diese Gleichung eine Q-Learning-Einheit ist.
Jetzt müssen wir nur noch unseren Zustand aktualisieren und alles ist fertig, dies ist Zeile 20. Wir wiederholen diesen Vorgang, bis wir das Ende der Episode erreichen, in den Felsen sterben oder das Ziel erreichen.
Fazit
Jetzt verstehen und verstehen wir intuitiv, wie man Q-Learning codiert (zumindest eine tabellarische Version). Überprüfen Sie unbedingt den gesamten Code, der für diesen Beitrag verwendet wird und auf GitHub verfügbar ist.
Visualisierung des Lernprozesstests:
Bitte beachten Sie, dass alle Aktionen mit einem Wert beginnen, der den Endwert überschreitet. Dies ist ein Trick, um die Erforschung der Welt anzuregen.