Wir haben bereits die PostgreSQL- Indexierungs-Engine und die Schnittstelle der Zugriffsmethoden sowie den Hash-Index , eine der Zugriffsmethoden, erörtert. Wir werden nun B-Tree betrachten, den traditionellsten und am weitesten verbreiteten Index. Dieser Artikel ist groß, seien Sie also geduldig.

Btree

Struktur

Der als "btree" -Zugriffsmethode implementierte B-Tree-Indextyp eignet sich für Daten, die sortiert werden können. Mit anderen Worten, für den Datentyp müssen die Operatoren "größer", "größer oder gleich", "kleiner", "kleiner oder gleich" und "gleich" definiert werden. Beachten Sie, dass dieselben Daten manchmal unterschiedlich sortiert werden können, was uns zum Konzept der Operatorfamilie zurückführt .

Wie immer werden Indexzeilen des B-Baums in Seiten gepackt. Auf Blattseiten enthalten diese Zeilen zu indizierende Daten (Schlüssel) und Verweise auf Tabellenzeilen (TIDs). Auf internen Seiten verweist jede Zeile auf eine untergeordnete Seite des Index und enthält den Mindestwert auf dieser Seite.

B-Bäume haben einige wichtige Eigenschaften:

• B-Bäume sind ausgeglichen, dh jede Blattseite ist durch die gleiche Anzahl interner Seiten vom Stamm getrennt. Daher dauert die Suche nach einem Wert dieselbe Zeit.
  
• B-Bäume sind mehrfach verzweigt, dh jede Seite (normalerweise 8 KB) enthält viele (Hunderte) TIDs. Infolgedessen ist die Tiefe von B-Bäumen ziemlich gering, bei sehr großen Tischen sogar bis zu 4–5.
  
• Die Daten im Index werden in nicht abnehmender Reihenfolge (sowohl zwischen den Seiten als auch innerhalb jeder Seite) sortiert, und Seiten derselben Ebene sind durch eine bidirektionale Liste miteinander verbunden. Daher können wir einen geordneten Datensatz nur durch eine Liste erhalten, die in die eine oder andere Richtung geht, ohne jedes Mal zur Wurzel zurückzukehren.
  

Unten finden Sie ein vereinfachtes Beispiel für den Index eines Felds mit Ganzzahlschlüsseln.



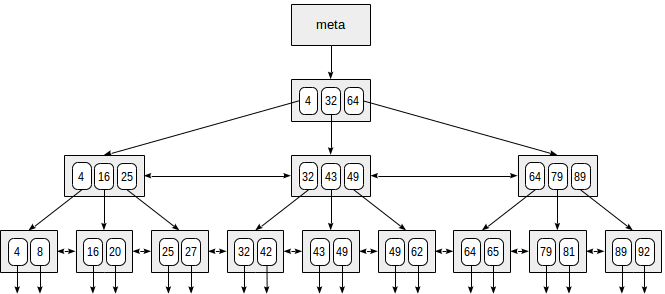
Die allererste Seite des Index ist eine Metapage, die auf den Indexstamm verweist. Interne Knoten befinden sich unterhalb des Stamms, und Blattseiten befinden sich in der untersten Zeile. Abwärtspfeile repräsentieren Verweise von Blattknoten auf Tabellenzeilen (TIDs).

Suche nach Gleichheit

Betrachten wir die Suche nach einem Wert in einem Baum nach der Bedingung " indexed-field = expression ". Sagen wir, wir interessieren uns für den Schlüssel von 49.



Die Suche beginnt mit dem Wurzelknoten, und wir müssen bestimmen, zu welchem ​​der untergeordneten Knoten abzusteigen ist. Da wir die Schlüssel im Stammknoten (4, 32, 64) kennen, ermitteln wir die Wertebereiche in untergeordneten Knoten. Da 32 ≤ 49 <64 ist, müssen wir zum zweiten untergeordneten Knoten absteigen. Als nächstes wird der gleiche Vorgang rekursiv wiederholt, bis wir einen Blattknoten erreichen, von dem die benötigten TIDs erhalten werden können.

In Wirklichkeit erschweren eine Reihe von Einzelheiten diesen scheinbar einfachen Prozess. Ein Index kann beispielsweise nicht eindeutige Schlüssel enthalten und es können so viele gleiche Werte vorhanden sein, dass sie nicht auf eine Seite passen. Zurück zu unserem Beispiel: Es scheint, dass wir vom internen Knoten über den Verweis auf den Wert 49 absteigen sollten. Wie aus der Abbildung hervorgeht, überspringen wir auf diese Weise einen der "49" -Schlüssel auf der vorhergehenden Blattseite . Sobald wir auf einer internen Seite einen genau gleichen Schlüssel gefunden haben, müssen wir eine Position nach links absteigen und dann die Indexzeilen der zugrunde liegenden Ebene von links nach rechts durchsuchen, um nach dem gesuchten Schlüssel zu suchen.

(Eine weitere Komplikation besteht darin, dass während der Suche andere Prozesse die Daten ändern können: Der Baum kann neu erstellt werden, Seiten können in zwei Teile geteilt werden usw. Alle Algorithmen sind so konzipiert, dass diese gleichzeitigen Vorgänge sich nicht gegenseitig stören und keine zusätzlichen Sperren verursachen wo immer möglich. Aber wir werden es vermeiden, darauf einzugehen.)

Suche nach Ungleichung

Bei der Suche nach der Bedingung " indiziertes Feld ≤ Ausdruck " (oder " indiziertes Feld ≥ Ausdruck ") finden wir zuerst einen Wert (falls vorhanden) im Index durch die Gleichheitsbedingung " indiziertes Feld = Ausdruck " und gehen dann durch Blattseiten in die entsprechende Richtung bis zum Ende.

Die Abbildung zeigt diesen Vorgang für n ≤ 35:



Die Operatoren "größer" und "kleiner" werden auf ähnliche Weise unterstützt, außer dass der ursprünglich gefundene Wert gelöscht werden muss.

Suche nach Bereich

Wenn wir nach dem Bereich " Ausdruck1 ≤ indiziertes Feld ≤ Ausdruck2 " suchen, finden wir einen Wert nach Bedingung " indiziertes Feld = Ausdruck1 " und gehen dann weiter durch Blattseiten, während die Bedingung " indiziertes Feld ≤ Ausdruck2 " erfüllt ist. oder umgekehrt: Beginnen Sie mit dem zweiten Ausdruck und gehen Sie in die entgegengesetzte Richtung, bis wir den ersten Ausdruck erreichen.

Die Abbildung zeigt diesen Vorgang für Bedingung 23 ≤ n ≤ 64:

Beispiel

Schauen wir uns ein Beispiel an, wie Abfragepläne aussehen. Wie üblich verwenden wir die Demo-Datenbank und dieses Mal betrachten wir die Flugzeugtabelle. Es enthält nur neun Zeilen, und der Planer würde den Index nicht verwenden, da die gesamte Tabelle auf eine Seite passt. Diese Tabelle ist jedoch zur Veranschaulichung für uns interessant.

demo=# select * from aircrafts; 

  aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows) 

 demo=# create index on aircrafts(range); demo=# set enable_seqscan = off; 

(Oder explizit "Index für Flugzeuge mit btree (range) erstellen", aber es ist ein B-Baum, der standardmäßig erstellt wird.)

Suche nach Gleichheit:

 demo=# explain(costs off) select * from aircrafts where range = 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows) 

Suche nach Ungleichung:

 demo=# explain(costs off) select * from aircrafts where range < 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows) 

Und nach Reichweite:

 demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000; 

  QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows) 

Sortieren

Lassen Sie uns noch einmal den Punkt hervorheben, dass bei jeder Art von Scan (Index, Nur-Index oder Bitmap) die Zugriffsmethode "btree" geordnete Daten zurückgibt, die wir in den obigen Abbildungen deutlich sehen können.

Wenn eine Tabelle einen Index für die Sortierbedingung hat, berücksichtigt der Optimierer daher beide Optionen: Index-Scan der Tabelle, die leicht sortierte Daten zurückgibt, und sequentieller Scan der Tabelle mit anschließender Sortierung des Ergebnisses.

Sortierreihenfolge

Beim Erstellen eines Index können wir die Sortierreihenfolge explizit angeben. Zum Beispiel können wir auf diese Weise einen Index nach Flugbereichen erstellen, insbesondere:

 demo=# create index on aircrafts(range desc); 

In diesem Fall werden links im Baum größere Werte angezeigt, während rechts kleinere Werte angezeigt werden. Warum kann dies erforderlich sein, wenn wir indizierte Werte in beide Richtungen durchlaufen können?

Der Zweck sind mehrspaltige Indizes. Erstellen wir eine Ansicht, um Flugzeugmodelle mit einer konventionellen Unterteilung in Kurz-, Mittel- und Langstreckenfahrzeuge zu zeigen:

 demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v; 

  model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows) 

Und lassen Sie uns einen Index erstellen (mit dem Ausdruck):

 demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model); 

Jetzt können wir diesen Index verwenden, um Daten nach beiden Spalten in aufsteigender Reihenfolge zu sortieren:

 demo=# select class, model from aircrafts_v order by class, model; 

  class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class, model; 

  QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row) 

Ebenso können wir die Abfrage ausführen, um Daten in absteigender Reihenfolge zu sortieren:

 demo=# select class, model from aircrafts_v order by class desc, model desc; 

  class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row) 

Wir können diesen Index jedoch nicht verwenden, um Daten nach einer Spalte in absteigender Reihenfolge und nach der anderen Spalte in aufsteigender Reihenfolge zu sortieren. Dies erfordert eine separate Sortierung:

 demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows) 

(Beachten Sie, dass der Planer als letzten Ausweg den sequentiellen Scan unabhängig von der zuvor vorgenommenen Einstellung "enable_seqscan = off" gewählt hat. Dies liegt daran, dass diese Einstellung das Scannen von Tabellen nicht verbietet, sondern nur die astronomischen Kosten festlegt - sehen Sie sich den Plan mit an "Kosten an".)

Damit diese Abfrage den Index verwendet, muss dieser mit der erforderlichen Sortierrichtung erstellt werden:

 demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row) 

Reihenfolge der Spalten

Ein weiteres Problem, das bei der Verwendung mehrspaltiger Indizes auftritt, ist die Reihenfolge der Auflistung der Spalten in einem Index. Für B-Tree ist diese Reihenfolge von großer Bedeutung: Die Daten innerhalb der Seiten werden nach dem ersten Feld, dann nach dem zweiten usw. sortiert.

Wir können den Index, den wir auf Entfernungsintervallen und Modellen aufgebaut haben, symbolisch wie folgt darstellen:



Tatsächlich passt ein so kleiner Index mit Sicherheit auf eine Stammseite. In der Abbildung ist es der Übersichtlichkeit halber bewusst auf mehrere Seiten verteilt.

Aus diesem Diagramm geht hervor, dass die Suche nach Prädikaten wie "class = 3" (Suche nur nach dem ersten Feld) oder "class = 3 und model = 'Boeing 777-300'" (Suche nach beiden Feldern) effizient funktioniert.

Die Suche nach dem Prädikat "model = 'Boeing 777-300'" ist jedoch weitaus weniger effizient: Ausgehend von der Wurzel können wir nicht bestimmen, zu welchem ​​untergeordneten Knoten abzusteigen ist, daher müssen wir zu allen absteigen. Dies bedeutet nicht, dass ein solcher Index niemals verwendet werden kann - es geht um seine Effizienz. Wenn wir zum Beispiel drei Flugzeugklassen und sehr viele Modelle in jeder Klasse hätten, müssten wir ungefähr ein Drittel des Index durchsehen, und dies wäre möglicherweise effizienter gewesen als der vollständige Tabellenscan ... oder nicht.

Wenn wir jedoch einen Index wie diesen erstellen:

 demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end)); 

Die Reihenfolge der Felder ändert sich:



Mit diesem Index funktioniert die Suche nach dem Prädikat "model = 'Boeing 777-300'" effizient, die Suche nach dem Prädikat "class = 3" jedoch nicht.

Nullen

Die Zugriffsmethode "Btree" indiziert NULL-Werte und unterstützt die Suche nach den Bedingungen IS NULL und IS NOT NULL.

Betrachten wir die Tabelle der Flüge, in denen NULL-Werte auftreten:

 demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null; 

  QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows) 

NULL-Werte befinden sich am einen oder anderen Ende der Blattknoten, je nachdem, wie der Index erstellt wurde (NULLS FIRST oder NULLS LAST). Dies ist wichtig, wenn eine Abfrage eine Sortierung enthält: Der Index kann verwendet werden, wenn der Befehl SELECT in seiner ORDER BY-Klausel dieselbe Reihenfolge von NULL-Werten angibt wie die für den erstellten Index angegebene Reihenfolge (NULLS FIRST oder NULLS LAST).

Im folgenden Beispiel sind diese Ordnungen gleich, daher können wir den Index verwenden:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST; 

  QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row) 

Und hier sind diese Reihenfolgen unterschiedlich, und der Optimierer wählt den sequentiellen Scan mit anschließender Sortierung:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows) 

Um den Index verwenden zu können, muss er mit NULL-Werten am Anfang erstellt werden:

 demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row) 

Probleme wie dieses werden sicherlich dadurch verursacht, dass NULL-Werte nicht sortierbar sind, dh das Ergebnis des Vergleichs für NULL und andere Werte ist undefiniert:

 demo=# \pset null NULL demo=# select null < 42; 

  ?column? ---------- NULL (1 row) 

Dies widerspricht dem Konzept des B-Baums und passt nicht in das allgemeine Muster. NULL-Werte spielen jedoch in Datenbanken eine so wichtige Rolle, dass wir immer Ausnahmen für sie machen müssen.

Da NULL-Werte indiziert werden können, ist es möglich, einen Index auch ohne Bedingungen für die Tabelle zu verwenden (da der Index sicher Informationen zu allen Tabellenzeilen enthält). Dies kann sinnvoll sein, wenn für die Abfrage eine Datenreihenfolge erforderlich ist und der Index die erforderliche Reihenfolge sicherstellt. In diesem Fall kann der Planer eher den Indexzugriff auswählen, um bei einer separaten Sortierung zu speichern.

Eigenschaften

Schauen wir uns die Eigenschaften der Zugriffsmethode "btree" an (Abfragen wurden bereits bereitgestellt ).

  amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t 

Wie wir gesehen haben, kann B-tree Daten bestellen und unterstützt die Eindeutigkeit - und dies ist die einzige Zugriffsmethode, die uns solche Eigenschaften bietet. Mehrspaltige Indizes sind ebenfalls zulässig, aber andere Zugriffsmethoden (obwohl nicht alle) unterstützen möglicherweise auch solche Indizes. Wir werden das nächste Mal die Unterstützung der EXCLUDE-Einschränkung diskutieren, und das nicht ohne Grund.

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t 

Die Zugriffsmethode "Btree" unterstützt beide Techniken zum Abrufen von Werten: Index-Scan sowie Bitmap-Scan. Und wie wir sehen konnten, kann die Zugriffsmethode sowohl "vorwärts" als auch "rückwärts" durch den Baum laufen.

  name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t 

Die ersten vier Eigenschaften dieser Ebene erklären, wie genau die Werte einer bestimmten Spalte geordnet sind. In diesem Beispiel werden die Werte in aufsteigender Reihenfolge ("asc") sortiert und die NULL-Werte werden zuletzt angegeben ("nulls_last"). Aber wie wir bereits gesehen haben, sind andere Kombinationen möglich.

Die Eigenschaft "Search_array" gibt die Unterstützung solcher Ausdrücke durch den Index an:

 demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773'); 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows) 

Die Eigenschaft "Returnable" gibt die Unterstützung des Nur-Index-Scans an, was sinnvoll ist, da Zeilen des Index selbst indizierte Werte speichern (im Gegensatz zum Beispiel im Hash-Index). Hier ist es sinnvoll, ein paar Worte zum Abdecken von Indizes zu sagen, die auf dem B-Baum basieren.

Eindeutige Indizes mit zusätzlichen Zeilen

Wie bereits erwähnt , ist ein Abdeckungsindex derjenige, der alle für eine Abfrage erforderlichen Werte speichert, wobei der Zugriff auf die Tabelle selbst (fast) nicht erforderlich ist. Ein eindeutiger Index kann speziell abdecken.

Nehmen wir jedoch an, wir möchten dem eindeutigen Index zusätzliche Spalten hinzufügen, die für eine Abfrage erforderlich sind. Die Eindeutigkeit solcher zusammengesetzter Werte garantiert jedoch nicht die Eindeutigkeit des Schlüssels, und dann werden zwei Indizes für dieselben Spalten benötigt: einer eindeutig zur Unterstützung der Integritätsbeschränkung und ein anderer zur Abdeckung. Dies ist sicher ineffizient.

In unserer Firma hat Anastasiya Lubennikova lubennikovaav die "btree" -Methode verbessert, sodass zusätzliche, nicht eindeutige Spalten in einen eindeutigen Index aufgenommen werden können. Wir hoffen, dass dieser Patch von der Community übernommen wird, um Teil von PostgreSQL zu werden. Dies wird jedoch nicht bereits in Version 10 geschehen. Derzeit ist der Patch in Pro Standard 9.5+ verfügbar, und so sieht er aus wie.

Tatsächlich wurde dieser Patch für PostgreSQL 11 festgelegt.

Betrachten wir die Buchungstabelle:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

In dieser Tabelle wird der Primärschlüssel (book_ref, Buchungscode) durch einen regulären "btree" -Index bereitgestellt. Erstellen wir einen neuen eindeutigen Index mit einer zusätzlichen Spalte:

 demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date); 

Jetzt ersetzen wir den vorhandenen Index durch einen neuen (in der Transaktion, um alle Änderungen gleichzeitig anzuwenden):

 demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit; 

Das bekommen wir:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

Jetzt funktioniert ein und derselbe Index als eindeutig und dient als Deckungsindex für diese Abfrage, zum Beispiel:

 demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4'; 

  QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows) 

Erstellung des Index

Es ist bekannt, aber nicht weniger wichtig, dass es für eine große Tabelle besser ist, dort Daten ohne Indizes zu laden und die erforderlichen Indizes später zu erstellen. Dies ist nicht nur schneller, sondern der Index wird höchstwahrscheinlich auch kleiner sein.

Die Sache ist, dass die Erstellung des "btree" -Index einen effizienteren Prozess verwendet als das zeilenweise Einfügen von Werten in den Baum. Grob gesagt werden alle in der Tabelle verfügbaren Daten sortiert und Blattseiten dieser Daten erstellt. Dann werden interne Seiten über diese Basis "aufgebaut", bis die gesamte Pyramide zur Wurzel konvergiert.

Die Geschwindigkeit dieses Vorgangs hängt von der Größe des verfügbaren Arbeitsspeichers ab, die durch den Parameter "tenance_work_mem "begrenzt wird. Das Erhöhen des Parameterwerts kann den Prozess beschleunigen. Bei eindeutigen Indizes wird zusätzlich zu "tenance_work_mem "Speicher der Größe" work_mem "zugewiesen.

Vergleichssemantik

Das letzte Mal haben wir erwähnt, dass PostgreSQL wissen muss, welche Hash-Funktionen Werte verschiedener Typen aufrufen sollen, und dass diese Zuordnung in der "Hash" -Zugriffsmethode gespeichert ist. Ebenso muss das System herausfinden, wie Werte bestellt werden. Dies wird für Sortierungen, Gruppierungen (manchmal), Zusammenführen von Verknüpfungen usw. benötigt. PostgreSQL bindet sich nicht an Operatornamen (wie>, <, =), da Benutzer ihren eigenen Datentyp definieren und entsprechenden Operatoren unterschiedliche Namen geben können. Eine von der Zugriffsmethode "btree" verwendete Operatorfamilie definiert stattdessen Operatornamen.

Diese Vergleichsoperatoren werden beispielsweise in der Operatorfamilie "bool_ops" verwendet:

 postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy; 

  opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows) 

Hier sehen wir fünf Vergleichsoperatoren, aber wie bereits erwähnt, sollten wir uns nicht auf deren Namen verlassen. Um herauszufinden, welchen Vergleich jeder Bediener durchführt, wird das Strategiekonzept eingeführt. Zur Beschreibung der Operatorsemantik sind fünf Strategien definiert:

• 1 - weniger
• 2 - weniger oder gleich
• 3 - gleich
• 4 - größer oder gleich
• 5 - größer

Einige Operatorfamilien können mehrere Operatoren enthalten, die eine Strategie implementieren. Beispielsweise enthält die Operatorfamilie "integer_ops" die folgenden Operatoren für Strategie 1:

 postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator; 

  opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows) 

Dank dessen kann der Optimierer beim Vergleichen von Werten verschiedener Typen, die in einer Operatorfamilie enthalten sind, Typumwandlungen vermeiden.

Indexunterstützung für einen neuen Datentyp

Die Dokumentation enthält ein Beispiel für die Erstellung eines neuen Datentyps für komplexe Zahlen und einer Operatorklasse zum Sortieren von Werten dieses Typs. In diesem Beispiel wird die Sprache C verwendet, was bei kritischer Geschwindigkeit absolut sinnvoll ist. Nichts hindert uns jedoch daran, reines SQL für dasselbe Experiment zu verwenden, um nur zu versuchen, die Vergleichssemantik besser zu verstehen.

Erstellen wir einen neuen zusammengesetzten Typ mit zwei Feldern: Real- und Imaginärteil.

 postgres=# create type complex as (re float, im float); 

Wir können eine Tabelle mit einem Feld des neuen Typs erstellen und der Tabelle einige Werte hinzufügen:

 postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0)); 

Nun stellt sich die Frage: Wie ordne ich komplexe Zahlen, wenn für sie keine Ordnungsbeziehung im mathematischen Sinne definiert ist?

Wie sich herausstellt, sind für uns bereits Vergleichsoperatoren definiert:

 postgres=# select * from numbers order by x; 

  x -------- (0,10) (1,1) (1,3) (3 rows) 

Standardmäßig erfolgt die Sortierung für einen zusammengesetzten Typ komponentenweise: Erste Felder werden verglichen, dann zweite Felder usw., ungefähr so, wie Textzeichenfolgen zeichenweise verglichen werden. Wir können aber eine andere Reihenfolge definieren. Beispielsweise können komplexe Zahlen als Vektoren behandelt und nach dem Modul (Länge) geordnet werden, der als Quadratwurzel der Quadratsumme der Koordinaten berechnet wird (Satz von Pythagoras). Um eine solche Reihenfolge zu definieren, erstellen wir eine Hilfsfunktion, die den Modul berechnet:

 postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql; 

Jetzt definieren wir systematisch Funktionen für alle fünf Vergleichsoperatoren, die diese Hilfsfunktion verwenden:

 postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql; 

Und wir erstellen entsprechende Operatoren. Um zu veranschaulichen, dass sie nicht ">", "<" usw. heißen müssen, geben wir ihnen "seltsame" Namen.

 postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt); 

An dieser Stelle können wir Zahlen vergleichen:

 postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex; 

  ?column? ---------- t (1 row) 

Zusätzlich zu fünf Operatoren muss für die Zugriffsmethode "btree" eine weitere Funktion (übermäßig, aber praktisch) definiert werden: Sie muss -1, 0 oder 1 zurückgeben, wenn der erste Wert kleiner, gleich oder größer als der zweite ist eins. Diese Hilfsfunktion wird als Unterstützung bezeichnet. Für andere Zugriffsmethoden müssen möglicherweise andere Unterstützungsfunktionen definiert werden.

 postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql; 

Jetzt können wir eine Operatorklasse erstellen (und die gleichnamige Operatorfamilie wird automatisch erstellt):

 postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex); 

Jetzt funktioniert das Sortieren wie gewünscht:

 postgres=# select * from numbers order by x; 

  x -------- (1,1) (1,3) (0,10) (3 rows) 

Und es wird sicherlich vom "btree" -Index unterstützt.

Um das Bild zu vervollständigen, können Sie mithilfe dieser Abfrage Supportfunktionen erhalten:

 postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid; 

  amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row) 

Interna

Wir können die interne Struktur des B-Baums mit der Erweiterung "pageinspect" untersuchen.

 demo=# create extension pageinspect; 

Index-Metapage:

 demo=# select * from bt_metap('ticket_flights_pkey'); 

  magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row) 

Am interessantesten ist hier die Indexebene: Der Index für zwei Spalten für eine Tabelle mit einer Million Zeilen erfordert nur zwei Ebenen (ohne Root).

Statistische Informationen zu Block 164 (root):

 demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164); 

  type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row) 

Und die Daten im Block (das Feld "Daten", das hier der Bildschirmbreite geopfert wird, enthält den Wert des Indexschlüssels in binärer Darstellung):

 demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5; 

  itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows) 

Das erste Element bezieht sich auf Techniken und gibt die Obergrenze aller Elemente im Block an (ein Implementierungsdetail, das wir nicht besprochen haben), während die Daten selbst mit dem zweiten Element beginnen. Es ist klar, dass der unterste Knoten ganz links Block 163 ist, gefolgt von Block 323 und so weiter. Sie können wiederum mit denselben Funktionen untersucht werden.

Nach einer guten Tradition ist es nun sinnvoll, die Dokumentation, die README-Datei und den Quellcode zu lesen.

Eine weitere potenziell nützliche Erweiterung ist " amcheck ", die in PostgreSQL 10 enthalten sein wird. Für niedrigere Versionen können Sie sie von github herunterladen . Diese Erweiterung überprüft die logische Konsistenz von Daten in B-Bäumen und ermöglicht es uns, Fehler im Voraus zu erkennen.

Das stimmt, "amcheck" ist ein Teil von PostgreSQL ab Version 10.

Lesen Sie weiter .