Schließlich erschien ein russischsprachiger Leitfaden zur Julia-Sprache . Es bietet eine vollständige Einführung in die Sprache für diejenigen, die wenig Erfahrung in der Programmierung haben (der Rest wird für die allgemeine Entwicklung nützlich sein), eine Einführung in das maschinelle Lernen und eine Reihe von Aufgaben zur Konsolidierung des Materials.
Während der Suche bin ich auf einen Programmierkurs für Wirtschaftswissenschaftler gestoßen (neben Julia gibt es auch Python). Erfahrene können einen kurzen Kurs belegen oder das Buch Wie man wie ein Informatiker denkt lesen
Das Folgende ist eine Übersetzung von Material aus dem Blog von Christopher Rackauckas 7 Julia Gotchas und wie man mit ihnen umgeht
Lassen Sie mich zunächst sagen, dass Julia eine wunderbare Sprache ist. Ich liebe sie, das ist meine Meinung nach die mächtigste und intuitivste Sprache, die ich je benutzt habe. Dies ist zweifellos meine Lieblingssprache. Es gibt jedoch einige "Fallstricke", knifflige Kleinigkeiten, über die Sie Bescheid wissen müssen. Jede Sprache hat sie, und eines der ersten Dinge, die Sie tun müssen, um die Sprache zu beherrschen, ist herauszufinden, was sie sind und wie Sie sie vermeiden können. In diesem Beitrag möchten wir Ihnen helfen, diesen Prozess zu beschleunigen, indem Sie einige der häufigsten
Julia ist eine gute Sprache, um zu verstehen, was passiert, weil es keine Magie gibt. Julia-Entwickler wollten klar definierte Verhaltensregeln. Dies bedeutet, dass jedes Verhalten erklärt werden kann. Dies kann jedoch bedeuten, dass Sie Ihren Kopf anstrengen müssen, um zu verstehen, warum dies und nicht das andere geschieht. Deshalb werde ich nicht nur einige häufig auftretende Probleme skizzieren, sondern auch erklären, warum sie auftreten. Sie werden sehen, dass es einige sehr ähnliche Muster gibt, und sobald Sie sich ihrer bewusst werden, werden Sie keines von ihnen mehr vermasseln. Aus diesem Grund hat Julia eine etwas steilere Lernkurve im Vergleich zu einfacheren Sprachen wie MATLAB / R / Python . Sobald Sie dies jedoch gemeistert haben, können Sie Julias Lakonismus voll ausnutzen, um C / Fortran- Leistung zu erzielen. Jetzt tiefer graben.
Unerwartet: REPL (Terminal) hat einen globalen Geltungsbereich
Dies ist bei weitem das häufigste Problem, das von neuen Julia-Benutzern gemeldet wird. Jemand wird sagen: "Ich habe gehört, Julia ist schnell!", Öffnen Sie REPL, schreiben Sie schnell einen bekannten Algorithmus auf und führen Sie dieses Skript aus. Nach der Ausführung schauen sie auf die Zeit und sagen: "Warte eine Sekunde, warum ist es langsam, wie in Python?" Da dies ein so wichtiges und häufiges Problem ist, lassen Sie uns einige Zeit damit verbringen, die Gründe zu untersuchen, warum dies passiert, um herauszufinden, wie dies vermieden werden kann.
Ein kleiner Exkurs: Warum Julia schnell ist
Sie müssen verstehen, dass Julia nicht nur eine Zusammenstellung von Code ist, sondern auch eine Spezialisierung von Typen (dh eine Zusammenstellung von Code, der für diese Typen spezifisch ist). Lassen Sie mich noch einmal wiederholen: Julia ist nicht schnell, weil der Code mit dem JIT-Compiler kompiliert wird. Das Geheimnis der Geschwindigkeit ist vielmehr, dass typspezifischer Code kompiliert wird.
Wenn Sie eine vollständige Geschichte benötigen, lesen Sie einige der Notizen, die ich für das bevorstehende Seminar geschrieben habe . Die Typenspezifität wird durch das Grundprinzip von Julias Design bestimmt: Mehrfachversand . Wenn Sie den Code schreiben:
function f(a,b) return 2a+b end
Es scheint, dass dies nur eine f(2.0,3.0) , führt Julia den kompilierten Code aus, der zwei Gleitkommazahlen verwendet und 2a + b zurückgibt. Wenn Sie f(2,3) aufrufen, führt Julia einen weiteren kompilierten Code aus, der zwei Ganzzahlen akzeptiert und 2a + b zurückgibt. Die Funktion f ist eine Abstraktion oder Abkürzung für viele verschiedene Methoden, die dieselbe Form haben, und ein solches Schema der Verwendung des Symbols f zum Aufrufen all dieser verschiedenen Methoden wird als Mehrfachversand bezeichnet. Und das gilt überall: Der Operator + ist eine Funktion, die abhängig von den angezeigten Typen Methoden aufruft. Julia erhält tatsächlich seine Geschwindigkeit, weil der von ihr kompilierte Code seine Typen kennt und daher der kompilierte Code, der f (2.0,3.0) aufruft, genau der kompilierte Code ist, den Sie erhalten, wenn Sie dieselbe Funktion in C / Fortran definieren . Sie können dies mit dem Makro code_native überprüfen, um die kompilierte Assembly code_native :
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
Dies ist dieselbe kompilierte Assembly, die Sie von einer Funktion in C / Fortran erwarten, und sie unterscheidet sich vom Assemblycode für Ganzzahlen:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
Essenz: REPL / Global Scope erlaubt keine Typspezifität
Dies bringt uns zum Hauptpunkt: REPL / Global Scope ist langsam, da es keine Typspezifikation zulässt. Beachten Sie zunächst, dass REPL ein globaler Bereich ist, da Julia einen verschachtelten Bereich für Funktionen zulässt. Zum Beispiel, wenn wir definieren
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
Wir werden sehen, dass dieser Code funktioniert. Dies liegt daran, dass Sie mit Julia
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
und
a = 2; b = 3 ans2= linearcombo()
Frage: Welche Typen sollte der Compiler für a und b akzeptieren? Beachten Sie, dass wir in diesem Beispiel die Typen geändert und trotzdem dieselbe Funktion aufgerufen haben. Es kann mit allen Typen umgehen, die wir hinzufügen: Floating, Ganzzahlen, Arrays, seltsame Benutzertypen usw. In der Julia-Sprache bedeutet dies, dass die Variablen eingerahmt werden müssen und die Typen bei jeder Verwendung überprüft werden. Wie sieht der kompilierte Code aus?
Sperrig pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
Für dynamische Sprachen ohne Typenspezialisierung ist dieser aufgeblähte Code mit allen zusätzlichen Anweisungen so gut wie möglich, sodass Julia langsamer wird. Um zu verstehen, warum dies so wichtig ist, beachten Sie, dass jeder Code, den Sie in Julia schreiben, kompiliert wird. Angenommen, Sie schreiben eine Schleife in Ihr Skript:
a = 1 for i = 1:100 a += a + f(a) end
Der Compiler muss diese Schleife kompilieren. Da er jedoch nicht garantieren kann, dass sich die Typen nicht ändern, wird alle Typen konservativ mit einem Fußtuch umwickelt, was zu einer langsamen Ausführung führt.
So vermeiden Sie ein Problem
Es gibt verschiedene Möglichkeiten, um dieses Problem zu vermeiden. Am einfachsten ist es, Ihre Skripte immer in Funktionen zu verpacken. Der vorherige Code hat beispielsweise die Form:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
Dies führt zu demselben Ergebnis. Da sich der Compiler jedoch auf Typ a spezialisieren kann, wird der gewünschte kompilierte Code bereitgestellt. Sie können Ihre Variablen auch als Konstanten definieren.
const b = 5
Auf diese Weise teilen Sie dem Compiler mit, dass sich die Variable nicht ändert, und können so den gesamten Code, der sie verwendet, auf den aktuellen Typ spezialisieren. Es gibt eine kleine Eigenart, dass Julia es Ihnen tatsächlich erlaubt, den Wert einer Konstante zu ändern, aber keinen Typ. Daher können Sie const , um dem Compiler mitzuteilen, dass Sie den Typ nicht ändern werden. Beachten Sie jedoch, dass es einige kleine Macken gibt:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
Dies funktioniert nicht wie erwartet, da der Compiler, der erkennt, dass er die Antwort auf f () = a kennt (da a eine Konstante ist), einfach den Funktionsaufruf durch die Antwort ersetzt und ein anderes Verhalten ergibt, als wenn a nicht konstant wäre.
Moral: Schreiben Sie Ihre Skripte nicht direkt in REPL, sondern verpacken Sie sie immer in eine Funktion.
Nezhdanchik zwei: Typinstabilität
Daher habe ich gerade eine Meinung dazu geäußert, wie wichtig die Codespezialisierung für Datentypen ist. Lassen Sie mich eine Frage stellen, was passiert, wenn sich Ihre Typen ändern können? Wenn Sie vermutet haben: „In diesem Fall können Sie den kompilierten Code nicht spezialisieren“, haben Sie Recht. Ein solches Problem ist als Typinstabilität bekannt. Sie können unterschiedlich aussehen, aber ein häufiges Beispiel ist, dass Sie den Wert mit dem einfachen, aber nicht unbedingt dem Typ initialisieren, der er sein sollte. Schauen wir uns zum Beispiel an:
function g() x=1 for i = 1:10 x = x/2 end return x end
Beachten Sie, dass 1/2 eine Gleitkommazahl in Julia ist. Wenn wir also mit x = 1 , ändert sich die Ganzzahl in eine Gleitkommazahl, und daher sollte die Funktion die innere Schleife so kompilieren, als ob sie von einem beliebigen Typ sein könnte. Wenn wir stattdessen hätten:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
Dann kann die gesamte Funktion optimal kompiliert werden, da x eine Gleitkommazahl bleibt (diese Fähigkeit des Compilers, Typen zu bestimmen, wird als Typinferenz bezeichnet). Wir können den kompilierten Code überprüfen, um den Unterschied festzustellen:
Einheimisches Fußtuch pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
gegen
Ordentlicher Assembler-Zauber pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
Solch ein Unterschied in der Anzahl der Berechnungen, um den gleichen Wert zu erhalten!
Wie man Typinstabilität findet und damit umgeht

An dieser Stelle könnten Sie fragen: "Warum nicht einfach C verwenden, damit Sie nicht nach diesen Instabilitäten suchen müssen?" Die Antwort lautet:
- Leicht zu finden
- Sie können hilfreich sein.
Sie können mit Instabilität mit Funktionsbarrieren umgehen
Julia gibt Ihnen das Makro code_warntype zu zeigen, wo sich code_warntype befinden. Wenn wir dies beispielsweise in der von uns erstellten g Funktion verwenden:
@code_warntype g()
Holen Sie sich die Analyse Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
Beachten Sie, dass wir am Anfang sagen, dass Typ x Any . Es wird jeder Typ verwendet, der nicht als strict type bezeichnet ist, dh es handelt sich um einen abstrakten Typ, der bei jedem Schritt eingerahmt / aktiviert werden muss. Wir sehen, dass wir am Ende x als UNION {FLOAT64, INT64} , was ein weiterer nicht strenger Typ ist. Dies sagt uns, dass sich Typ code_warntype für h , erhalten wir alle strengen Typen:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
Dies zeigt an, dass die Funktion typstabil ist und im Wesentlichen zu einem optimalen C-Code kompiliert wird . Daher ist eine Typinstabilität nicht schwer zu finden. Schwieriger ist es, das richtige Design zu finden. Warum Typinstabilität beheben? Dies ist ein langjähriges Problem, das dazu geführt hat, dass dynamisch typisierte Sprachen das Spielfeld von Skripten dominieren. Die Idee ist, dass Sie in vielen Fällen einen Kompromiss zwischen Leistung und Zuverlässigkeit finden möchten.
Sie können beispielsweise eine Tabelle von einer Webseite lesen, auf der Ganzzahlen mit Gleitkommazahlen gemischt sind. In Julia können Sie Ihre Funktion so schreiben, dass sie gut kompiliert wird, wenn alle Ganzzahlen sind, und wenn alle Gleitkommazahlen sind, auch gut kompiliert. Und wenn sie gemischt sind? Dies wird immer noch funktionieren. Dies ist die Flexibilität / Bequemlichkeit, die wir aus einer Sprache wie Python / R kennen und lieben . Aber Julia wird Ihnen direkt ( über code_warntype ) mitteilen, wann Sie die Leistung opfern.
Umgang mit Typinstabilitäten
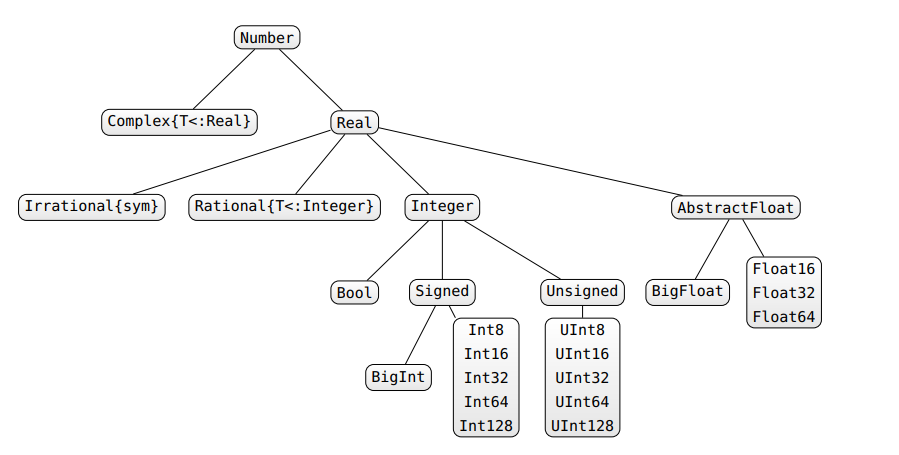
Es gibt verschiedene Möglichkeiten, mit Typinstabilitäten umzugehen. Wenn Sie etwas wie C / Fortran mögen, bei dem Ihre Typen deklariert sind und sich nicht ändern können (was die Typstabilität gewährleistet), können Sie dies zunächst in Julia tun:
local a::Int64 = 5
Dies ergibt a 64-Bit-Ganzzahl. Wenn zukünftiger Code versucht, sie zu ändern, wird eine Fehlermeldung generiert (oder die korrekte Konvertierung wird durchgeführt. Da die Konvertierung jedoch nicht automatisch gerundet wird, führt dies höchstwahrscheinlich zu Fehlern). Streuen Sie sie um Ihren Code und Sie erhalten Typstabilität, ala, C / Fortran . Eine weniger komplizierte Möglichkeit, dies zu handhaben, sind Typanweisungen. Hier setzen Sie die gleiche Syntax auf die andere Seite des Gleichheitszeichens. Zum Beispiel:
a = (b/c)::Float64
Es scheint zu sagen: "Berechnen Sie b / c und stellen Sie sicher, dass die Ausgabe Float64 ist. Wenn dies nicht der Fall ist, versuchen Sie, eine automatische Konvertierung durchzuführen. Wenn die Konvertierung nicht einfach durchgeführt werden kann, geben Sie einen Fehler aus." Durch das Platzieren solcher Designs können Sie sicherstellen, dass Sie wissen, um welche Typen es sich handelt. In einigen Fällen ist jedoch eine Typinstabilität erforderlich. Nehmen wir zum Beispiel an, Sie möchten zuverlässigen Code haben, aber der Benutzer gibt Ihnen etwas Verrücktes, wie:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
Dies ist ein Array von 4x1-Ganzzahlen und Gleitkommazahlen. Der eigentliche Elementtyp für das Array ist Union {Int64, Float64} , was, wie wir bereits gesehen haben, nicht streng war, was zu Problemen führen kann. Der Compiler weiß nur, dass jeder Wert eine Ganzzahl oder eine Gleitkommazahl sein kann, nicht jedoch welches Element von welchem Typ. Dies bedeutet, dass es naiv ist, mit diesem Array zu rechnen, zum Beispiel:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
wird langsam sein, da die Operationen boxed werden. Wir können jedoch mehrere Versendungen verwenden, um Codes auf spezielle Weise auszuführen. Dies wird als Verwendung von Funktionsbarrieren bezeichnet. Zum Beispiel:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
Beachten Sie, dass beim Aufrufen von inner_foo aufgrund des Mehrfachversands entweder eine speziell für Gleitkommazahlen kompilierte Methode oder eine speziell für Ganzzahlen kompilierte Methode inner_foo . Auf diese Weise können Sie eine lange Berechnung in inner_foo und trotzdem dafür sorgen, dass sie gut funktioniert, was der strengen Typisierung, die Ihnen die funktionale Barriere bietet, nicht unterlegen ist.
Daher hoffe ich, dass Sie sehen, dass Julia eine gute Kombination aus starker Tippleistung und dem Komfort des dynamischen Tippens bietet. Eine gute Programmiererin, Julia, hat beide Möglichkeiten, um die Produktivität und / oder Produktivität bei Bedarf zu maximieren.
Überraschung 3: Eval funktioniert global

Eine der größten Stärken von Julia ist ihre Metaprogrammierfähigkeit. Auf diese Weise können Sie problemlos Programme zur Codegenerierung schreiben und so die Menge an Code reduzieren, die Sie schreiben und warten müssen. Ein Makro ist eine Funktion, die zur Kompilierungszeit ausgeführt wird und (normalerweise) Code ausspuckt. Zum Beispiel:
macro defa() :(a=5) end
ersetzt jede defa Instanz durch den Code a = 5 ( :(a = 5) ist ein Ausdruck in Anführungszeichen . Julias Code besteht aus Ausdrücken, und daher ist die Metaprogrammierung eine Sammlung von Ausdrücken).
Sie können dies verwenden, um ein beliebiges komplexes Julia-Programm zu erstellen und es in eine Funktion als eine Art wirklich intelligente Verknüpfung einzufügen. Manchmal müssen Sie den generierten Code jedoch direkt auswerten. Julia gibt Ihnen dazu eine @eval oder ein @eval eval Makro. Im Allgemeinen sollten Sie versuchen, eine eval zu vermeiden, aber es gibt einige Codes, in denen dies erforderlich ist, z. B. meine neue Bibliothek zum Übertragen von Daten zwischen verschiedenen Prozessen für die parallele Programmierung . Beachten Sie jedoch Folgendes, wenn Sie es verwenden:
@eval :(a=5)
(REPL). , / . Zum Beispiel:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . Zum Beispiel:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. Zum Beispiel:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . Zum Beispiel:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . Zum Beispiel:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]