Algorithmen für Empfehlungen, Vorhersagen von Ereignissen oder Risikobewertungen sind eine Trendentscheidung in Banken, Versicherungsunternehmen und vielen anderen Geschäftsbereichen. Diese Programme helfen beispielsweise auf der Grundlage von Datenanalysen, anzugeben, wann ein Kunde einen Bankkredit zurückgeben wird, wie hoch die Nachfrage im Einzelhandel sein wird, wie hoch die Wahrscheinlichkeit eines versicherten Ereignisses oder ein Abfluss von Kunden in der Telekommunikation ist usw. Für ein Unternehmen ist dies eine wertvolle Gelegenheit, seine Ausgaben zu optimieren, die Arbeitsgeschwindigkeit zu erhöhen und den Service allgemein zu verbessern.
Traditionelle Ansätze wie Klassifizierung und Regression sind jedoch nicht für die Erstellung solcher Programme geeignet. Betrachten Sie dieses Problem als Beispiel für einen Fall, in dem medizinische Episoden vorhergesagt werden: Wir analysieren die Nuancen in der Natur von Daten und mögliche Ansätze zur Modellierung, erstellen ein Modell und analysieren dessen Qualität.
Die Herausforderung, medizinische Episoden vorherzusagen
Die Vorhersage von Episoden basiert auf einer Analyse historischer Daten. Der Datensatz besteht in diesem Fall aus zwei Teilen. Das erste sind Daten zu Dienstleistungen, die zuvor für den Patienten erbracht wurden. Dieser Teil des Datensatzes enthält soziodemografische Daten über den Patienten wie Alter und Geschlecht sowie Diagnosen, die zu unterschiedlichen Zeitpunkten in der ICD10-CM-Codierung [1] und den durchgeführten HCPCS-Verfahren [2] gestellt wurden. Diese Daten bilden zeitliche Sequenzen, mit denen Sie sich einen Überblick über den Zustand des Patienten zum Zeitpunkt des Interesses verschaffen können. Für Trainingsmodelle sowie für die Arbeit in der Produktion reichen personalisierte Daten aus.
Der zweite Teil des Datensatzes ist eine Liste der Episoden, die für den Patienten auftreten. Für jede Episode geben wir Art und Datum des Auftretens sowie den Zeitraum, einschließlich der Dienste und anderer Informationen an. Aus diesen Daten werden Zielvariablen für die Vorhersage generiert.
Der Aspekt der Zeit ist wichtig für die Lösung des Problems: Wir sind nur an Episoden interessiert, die in naher Zukunft auftreten können. Andererseits wurde der uns zur Verfügung stehende Datensatz für einen begrenzten Zeitraum gesammelt, über den hinaus keine Daten vorliegen. Wir können daher nicht sagen, ob Episoden außerhalb des Beobachtungszeitraums auftreten, um welche Episoden es sich handelt und zu welchem genauen Zeitpunkt sie auftreten. Diese Situation nennt man richtige Zensur.
In ähnlicher Weise tritt eine Linkszensur auf: Bei einigen Patienten kann sich eine Episode früher entwickeln, als dies für unsere Beobachtung verfügbar ist. Für uns wird es wie eine Episode aussehen, die ohne Hintergrund entstanden ist.
Es gibt eine andere Art der Datenzensur - die Unterbrechung der Beobachtung (wenn der Beobachtungszeitraum nicht abgeschlossen ist und das Ereignis nicht eingetreten ist). Zum Beispiel aufgrund eines sich bewegenden Patienten, eines Fehlers im Datenerfassungssystem und so weiter.
In Abb. 1 zeigt schematisch verschiedene Arten der Datenzensur. Sie alle verzerren Statistiken und erschweren die Erstellung eines Modells.
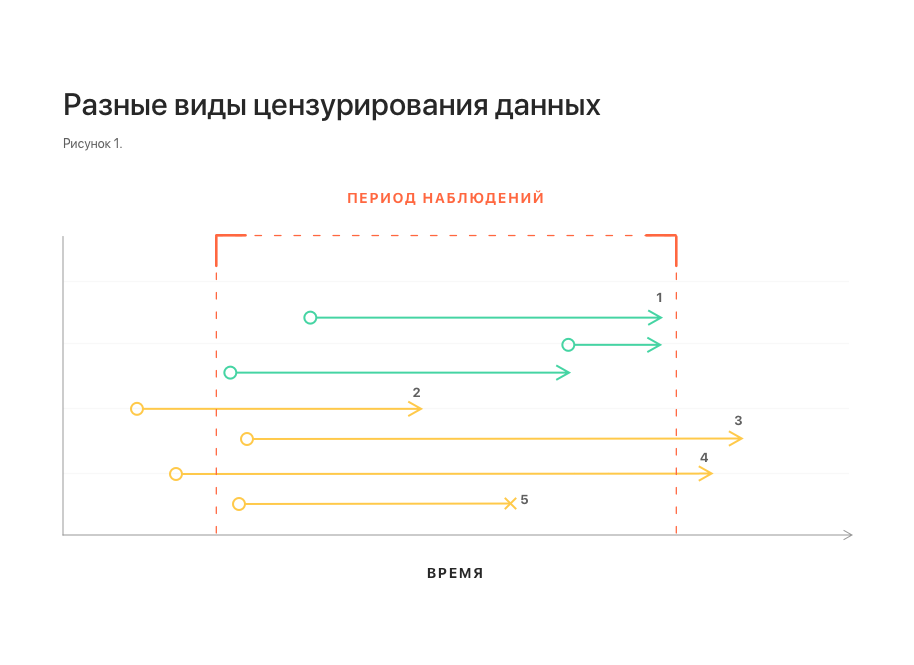Anmerkungen: 1 - unzensierte Beobachtungen; 2, 3 - linke bzw. rechte Zensur; 4 - linke und rechte Zensur gleichzeitig;
5 - Unterbrechung der Beobachtung.Ein weiteres wichtiges Merkmal des Datensatzes hängt mit der Art des Datenstroms im wirklichen Leben zusammen. Einige Daten kommen möglicherweise zu spät an. In diesem Fall sind sie zum Zeitpunkt der Vorhersage nicht verfügbar. Um diese Funktion zu berücksichtigen, muss der Datensatz ergänzt werden, indem mehrere Elemente aus dem Ende jeder Sequenz geworfen werden.
Klassifikation und Regression
Der erste Gedanke wird natürlich sein, das Problem auf die bekannte Klassifikation und Regression zu reduzieren. Diese Ansätze stoßen jedoch auf ernsthafte Schwierigkeiten.
Warum Regression nicht zu uns passt, geht aus den betrachteten Phänomenen der rechten und linken Zensur hervor: Die Verteilung des Zeitpunkts des Auftretens einer Episode im Datensatz kann verschoben werden. Darüber hinaus können die Größe und die Tatsache des Vorhandenseins dieser Verzerrung nicht unter Verwendung des Datensatzes selbst bestimmt werden. Das konstruierte Modell kann mit allen Validierungsansätzen beliebig gute Ergebnisse zeigen, dies hat jedoch höchstwahrscheinlich nichts mit seiner Eignung für die Prognose von Produktionsdaten zu tun.
Vielversprechender ist auf den ersten Blick der Versuch, das Problem auf die Klassifizierung zu reduzieren: einen bestimmten Zeitraum festzulegen und die Episode zu bestimmen, die in diesem Zeitraum auftreten wird. Die Hauptschwierigkeit hierbei ist die Bindung des für uns interessanten Zeitintervalls. Es kann nur mit dem Zeitpunkt der letzten Aktualisierung der Krankengeschichte des Patienten zuverlässig verknüpft werden. Gleichzeitig ist die Anfrage nach der Vorhersage der Episode überhaupt nicht an die Zeit gebunden und kann jederzeit sowohl innerhalb dieses Zeitraums (und dann verkürzt sich der effektive Zeitraum von Interesse) als auch vollständig außerhalb des Zeitraums erfolgen - und dann verliert die Vorhersage im Allgemeinen ihre Bedeutung (siehe Abb. 2). Dies führt natürlich zu einer Verlängerung des interessierenden Zeitraums, was letztendlich den Wert der Vorhersage ohnehin verringert.
Anmerkungen: 1 - aktualisiert die Krankengeschichte des Patienten; 2 - das neueste Update und die damit verbundene Zeitspanne; 3, 4 - Anfragen zur Vorhersage von Episoden, die während dieses Zeitraums eingegangen sind. Es ist ersichtlich, dass das effektive Vorhersageintervall für sie geringer ist; 5 - Anfrage außerhalb des Intervalls empfangen. Für ihn ist eine Vorhersage unmöglich.Überlebensanalyse
Alternativ können wir den in der russischen Literatur als Überlebensanalyse (Überlebensanalyse oder Time-to-Event-Analyse) bezeichneten Ansatz in Betracht ziehen [3]. Dies ist eine Modellfamilie, die speziell für die Arbeit mit zensierten Daten entwickelt wurde. Es basiert auf der Annäherung der Risikofunktion (Gefährdungsfunktion, Intensität des Auftretens von Ereignissen), die die Wahrscheinlichkeitsverteilung des Auftretens eines Ereignisses über die Zeit schätzt. Mit diesem Ansatz können Sie das Vorhandensein verschiedener Arten von Zensur korrekt berücksichtigen.
Für das zu lösende Problem ermöglicht dieser Ansatz zusätzlich die Kombination beider Aspekte des Problems in einem Modell: Bestimmen des Episodentyps und Vorhersagen des Zeitpunkts seines Auftretens. Zu diesem Zweck reicht es aus, für jeden Episodentyp ein eigenes Modell zu erstellen, ähnlich dem One-vs-All-Ansatz in der Klassifizierung. Dann kann das Auftreten einer Nicht-Ziel-Episode als Ausschluss eines Objekts aus der beobachteten Stichprobe ohne das Auftreten eines Ereignisses interpretiert werden, was eine andere Art der Zensur von Daten darstellt und auch vom Modell korrekt berücksichtigt wird. Diese Interpretation ist aus Sicht der Geschäftslogik richtig: Wenn sich ein Patient einer Kataraktoperation unterzieht, schließt dies das Auftreten anderer Episoden für ihn in der Zukunft nicht aus.
Innerhalb der Modellfamilie für die Überlebensanalyse können zwei Sorten unterschieden werden: analytische und Regression. Analytische Modelle sind rein beschreibend, sie sind für die gesamte Bevölkerung erstellt, berücksichtigen nicht die Merkmale ihrer einzelnen Mitglieder und können daher das Auftreten eines Ereignisses nur für ein typisches Mitglied der Bevölkerung vorhersagen. Im Gegensatz zu analytischen Modellen werden Regressionsmodelle unter Berücksichtigung der Merkmale einzelner Bevölkerungsmitglieder erstellt und ermöglichen Prognosen auch für einzelne Mitglieder unter Berücksichtigung ihrer Merkmale. Bei diesem Problem wurde diese Variante verwendet, oder vielmehr das Proportional Hazard-Modell von Cox (im Folgenden: CoxPH).
Überlebensregression und Kataraktoperation
Der einfachste Ansatz ähnelt der herkömmlichen Regression: Nehmen Sie die mathematische Erwartung des Zeitpunkts des Beginns des Ereignisses als Ausgabe. Da CoxPH am Eingang Daten als numerischen Vektor empfängt und unser Datensatz tatsächlich eine Folge von Diagnosecodes und -verfahren (kategoriale Daten) ist, ist eine vorläufige Datentransformation erforderlich:
- Übersetzung von Codes in eine eingebettete Darstellung unter Verwendung des zuvor trainierten GloVe-Modells [4];
- Aggregation aller in der letzten Periode der Patientenanamnese verfügbaren Codes zu einem einzigen Vektor;
- One-Hot-Codierung des Geschlechts eines Patienten und Skalierung des Alters.
Wir verwenden die erhaltenen Merkmalsvektoren für das Modelltraining und dessen Validierung. Das resultierende Modell zeigt die folgenden Konkordanzindexwerte (c-Index oder c-Statistik) [5]:
- 0,71 für 5-fache Validierung;
- 0,69 für die ausstehende Stichprobe.
Dies ist vergleichbar mit dem für solche Modelle üblichen Wert von 0,6–0,7 [6].
Wenn Sie sich jedoch den mittleren absoluten Fehler zwischen dem vorhergesagten erwarteten Zeitpunkt des Auftretens der Episode und dem tatsächlichen ansehen, stellt sich heraus, dass der Fehler 5 Tage beträgt. Der Grund für einen so großen Fehler ist, dass die Optimierung für den c-Index nur die richtige Reihenfolge der Werte garantiert: Sollte ein Ereignis früher als ein anderes auftreten, sind die vorhergesagten Werte der erwarteten Zeit bis zu Ereignissen jeweils kleiner als die anderen. Darüber hinaus werden keine Aussagen zu den vorhergesagten Werten selbst gemacht.
Eine weitere mögliche Variante des Ausgabewerts des Modells ist eine Wertetabelle der Risikofunktion zu verschiedenen Zeitpunkten. Diese Option hat eine komplexere Struktur, ist schwieriger zu interpretieren als die vorherige, bietet aber gleichzeitig mehr Informationen.
Das Ändern des Ausgabeformats erfordert eine andere Methode zur Bewertung der Qualität des Modells: Wir müssen sicherstellen, dass bei positiven Beispielen (wenn eine Episode auftritt) das Risiko höher ist als bei negativen Beispielen (wenn eine Episode nicht auftritt). Zu diesem Zweck wechseln wir für jede vorhergesagte Verteilung der Risikofunktion in der verzögerten Stichprobe von der Wertetabelle zu einem Wert - dem Maximum. Nachdem wir die Medianwerte für positive und negative Beispiele gezählt haben, werden wir sehen, dass sie sich zuverlässig unterscheiden: 0,13 gegenüber 0,04.
Als nächstes verwenden wir diese Werte, um die ROC-Kurve zu erstellen und die Fläche darunter zu berechnen - ROC AUC, die 0,92 beträgt, was für das zu lösende Problem akzeptabel ist.
Fazit
Daher haben wir gesehen, dass die Überlebensanalyse der beste Ansatz zur Lösung des Problems der Vorhersage medizinischer Episoden ist, wobei alle Nuancen des Problems und die verfügbaren Daten berücksichtigt werden. Die Anwendung impliziert jedoch ein anderes Format der Modellausgabedaten und einen anderen Ansatz zur Bewertung der Qualität.
Durch die Anwendung des CoxPH-Modells zur Vorhersage von Episoden einer Kataraktoperation konnten akzeptable Modellqualitätsindikatoren erzielt werden. Ein ähnlicher Ansatz kann auf andere Arten von Episoden angewendet werden, aber bestimmte Qualitätsindikatoren von Modellen können nur direkt im Modellierungsprozess bewertet werden.
Literatur
[1] ICD-10 Clinical Modification
de.wikipedia.org/wiki/ICD-10_Clinical_Modification[2] Codierungssystem für allgemeine Verfahren im Gesundheitswesen
de.wikipedia.org/wiki/Healthcare_Common_Procedure_Coding_System[3] Überlebensanalyse
en.wikipedia.org/wiki/Survival_analysis[4] GloVe: Globale Vektoren für die
Wortrepräsentation nlp.stanford.edu/projects/glove[5] C-Statistik: Definition, Beispiele, Gewichtung und Bedeutung
www.statisticshowto.datasciencecentral.com/c-statistic[6] VC Raykar et al. Zum Ranking in der Überlebensanalyse:
Grenzen des Konkordanzindex
paper.nips.cc/paper/3375-on-ranking-in-survival-analysis-bounds-on-the-concordance-index.pdf