Einführung:Mit der Anwendung von Bessel-Funktionen ist eine Vielzahl der unterschiedlichsten Probleme verbunden, die sich auf fast alle wichtigen Bereiche der mathematischen Physik beziehen und auf die Beantwortung aktueller technischer Fragen ausgelegt sind.
Bessel-Funktionen werden häufig zur Lösung von Problemen der Akustik, Radiophysik, Hydrodynamik sowie der Atom- und Kernphysik eingesetzt. Zahlreiche Anwendungen der Bessel-Funktionen auf die Theorie der Wärmeleitfähigkeit und die Theorie der Elastizität (Probleme bei Plattenschwingungen, Probleme der Schalentheorie, Probleme bei der Bestimmung der Spannungskonzentration in der Nähe von Rissen).
Diese Popularität von Bessel-Funktionen erklärt sich aus der Tatsache, dass das Lösen von Gleichungen der mathematischen Physik, die den Laplace-Operator in Zylinderkoordinaten enthalten, mit der klassischen Methode der Variablentrennung zu einer gewöhnlichen Differentialgleichung führt, die zur Bestimmung dieser Funktionen dient [1].
Bessel-Funktionen sind nach dem deutschen Astronomen Friedrich Bessel benannt, der 1824, als er die Bewegung von Planeten um die Sonne untersuchte, Wiederholungsrelationen für Bessel-Funktionen ableitete
Jv(x) für ganze Zahlen empfangen
v integrale Darstellung einer Funktion
Jv(x) bewies die Existenz unzähliger Funktionsnullen
J0(x) und kompilierte die ersten Tabellen für Funktionen
J1(x) und
J2(x) .
Zum ersten Mal jedoch eine der Funktionen von Bessel
J0(x) Es wurde bereits 1732 von Daniel Bernoulli in einer Arbeit über die Schwingung schwerer Ketten betrachtet. D. Bernoulli fand einen Ausdruck der Funktion
J0(x) in Form einer Potenzreihe und bemerkte (ohne Beweis), dass die Gleichung
J0(x)=0 hat unzählige gültige Wurzeln.
Die nächste Arbeit, in der Bessel-Funktionen angetroffen werden, war die Arbeit von Leonardo Euler im Jahr 1738, die sich mit der Untersuchung der Schwingungen einer kreisförmigen Membran befasste. In dieser Arbeit fand L. Euler für ganze Zahlen
v Bessel-Funktionsausdruck
Jv(x) in Form einer Reihe von Kräften
x und in nachfolgenden Veröffentlichungen wurde dieser Ausdruck auf den Fall beliebiger Indexwerte erweitert
v . Darüber hinaus hat L. Euler bewiesen, dass für
v gleich anderthalb ganze Zahlen, Funktionen
Jv(x) ausgedrückt durch elementare Funktionen.
Er bemerkte (ohne Beweise), dass mit gültig
v die Funktionen
Jv(x) habe unzählige reelle Nullen und gab eine ganzzahlige Darstellung für
Jv(x) . Einige Forscher glauben, dass die wichtigsten Ergebnisse in Bezug auf Bessel-Funktionen und ihre Anwendungen in der mathematischen Physik mit dem Namen L. Euler zusammenhängen.
Um die Eigenschaft von Bessel-Funktionen zu untersuchen und gleichzeitig Methoden zur Lösung von Gleichungen zu beherrschen, die auf Bessel-Funktionen reduziert sind, ermöglicht das frei verteilte Programm der symbolischen Mathematik SymPy - die Python-Bibliothek.
Im SymPy-Programm für symbolische Mathematik können Diagramme von Bessel-Funktionen der ersten Art von ganzzahligen Ordnungen unter Verwendung der Beziehung für die Summe einer Reihe erstellt werden:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gamma(p+m+1)
Bessel-Funktionen der ersten Artfrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
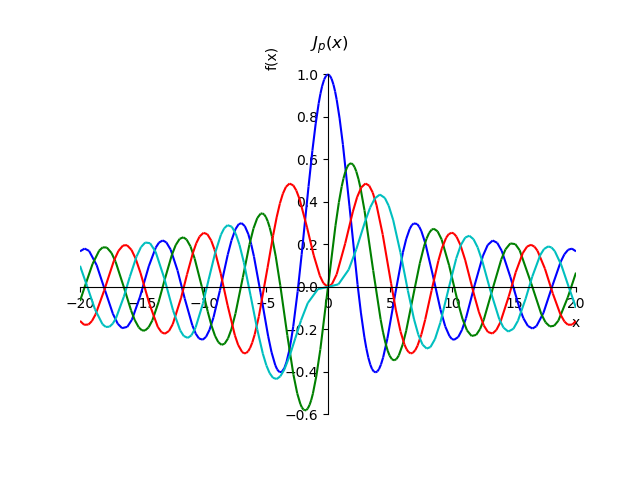
Mit der Beziehung für die Summe einer Reihe können wir die Eigenschaft dieser Funktionen für ganze Aufträge beweisen
J1(x)=−J−1(x):
Eigentum der Bessel-Funktion der ersten Art from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

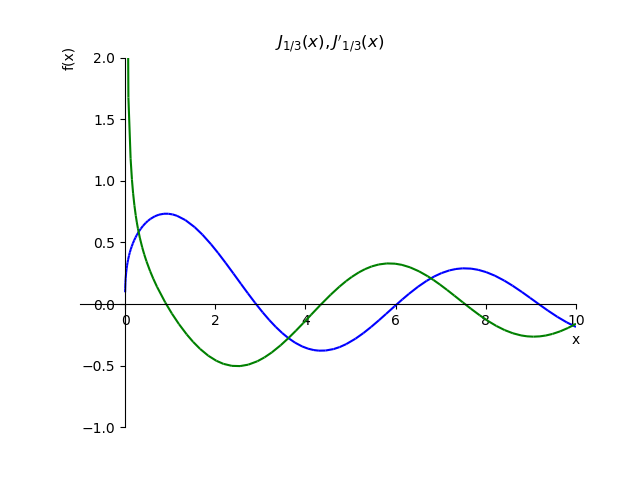
Um die Cauchy-Bedingungen zu demonstrieren, konstruieren wir eine Funktion
J1/3(x) und seine Ableitung
fracdJ1/3(x)dx: ::
Bruchordnungsfunktion und ihre Ableitung from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
Für praktische Berechnungen wird jedoch das wunderbare mpmath-Modul verwendet, mit dem nicht nur Gleichungen mit Bessel-Funktionen der ersten und zweiten Art numerisch gelöst werden können, einschließlich modifizierter Gleichungen aller zulässigen Ordnungen, sondern auch Diagramme mit automatischer Skalierung erstellt werden können.
Darüber hinaus benötigt das mpmath-Modul keine speziellen Tools für den Austausch symbolischer und numerischer Mathematik. Die Entstehungsgeschichte dieses Moduls und die Möglichkeit seiner Verwendung für die inverse Laplace-Transformation habe ich bereits in Veröffentlichung [2] betrachtet. Nun setzen wir die Diskussion über mpmath für die Arbeit mit Bessel-Funktionen fort [3].
Bessel-Funktion der ersten Art JN(x)mpmath.besselj (n, x, Ableitung = 0) - ergibt eine Bessel-Funktion der ersten Art
Jn(x) . Funktionen
JN(x) ist eine Lösung für die folgende Differentialgleichung:
x2y″+xy′+(x2−n2)y=0
Für das ganze Positive
n verhält sich wie ein Sinus oder Cosinus, multipliziert mit einem Koeffizienten, der langsam mit abnimmt
x rightarrow pm inftyBessel-Funktion der ersten Art
JN(x) ist ein Sonderfall der hypergeometrischen Funktion
oF1 ::
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1, fracx24)
Die Bessel-Funktion kann unterschieden werden
m Zeiten vorausgesetzt, dass die m-te Ableitung ungleich Null ist:
fracdmdxmJn(x)
Bessel-Funktion der ersten Art
JN(x) für positive ganzzahlige Ordnungen n = 0,1,2,3 - die Lösung der Bessel-Gleichung:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

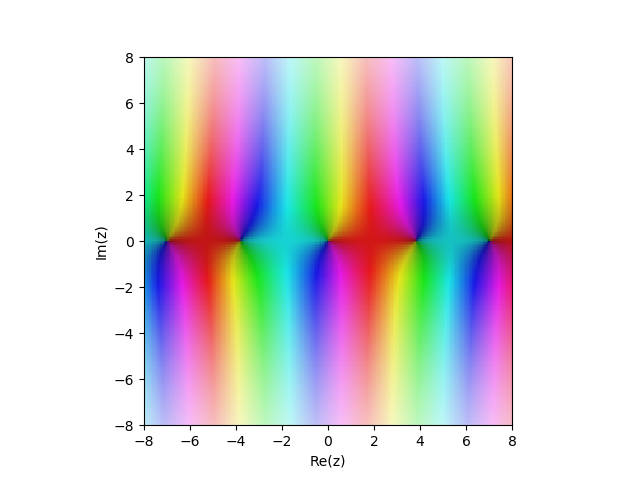
Bessel-Funktion der ersten Art
JN(x) in der komplexen Ebene:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
Beispiele:
Funktion
besselj(N,x) liefert ein Ergebnis mit einer bestimmten Anzahl von Ziffern
(mp.dps) nach dem Komma:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Ein Funktionsargument kann eine große Zahl sein:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
Bessel-Funktionen der ersten Art erfüllen einfache Symmetrien in Bezug auf
x=0 ::
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
Die Wurzeln sind nicht periodisch, aber der Abstand zwischen aufeinanderfolgenden Wurzeln nähert sich asymptotisch
2π . Bessel-Funktionen der ersten Art haben folgenden Code:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Für
n=1/2 oder
n=−1/2 Die Bessel-Funktion wird auf eine trigonometrische Funktion reduziert:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
Derivate jeder Ordnung können berechnet werden,
negative Ordnungen entsprechen der Integration :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
Die Differenzierung mit nicht ganzzahliger Ordnung ergibt eine gebrochene Ableitung im Sinne des Riemann-Liouville-Differentialintegrals, die unter Verwendung der Funktion berechnet wird
difint() ::
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Andere Möglichkeiten, die Bessel-Funktion der ersten Art von Null und erster Ordnung aufzurufen
mpmath.j0 (x) - Berechnet die Bessel-Funktion
J0(x) ;;
mpmath.j1 (x) - Berechnet die Bessel-Funktion
J1(x) ;;
Bessel-Funktionen der zweiten Artbessely (n, x, Ableitung = 0) Berechnet die Bessel-Funktion zweiter Art aus der Beziehung:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
Für eine ganze Zahl
n Die folgende Formel sollte als Grenze verstanden werden. Die Bessel-Funktion kann unterschieden werden
m Zeiten vorausgesetzt, dass die m-te Ableitung ungleich Null ist:
fracdmdxmYn(x)Bessel-Funktion der zweiten Art
Yn(x) für ganzzahlige positive Aufträge
n=0,1,2,3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
2. Art Bessel-Funktion
Yn(x) in der komplexen Ebene
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
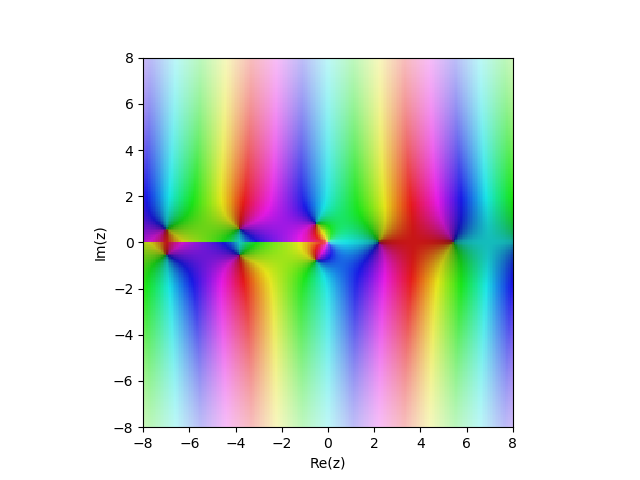
Beispiele:
Einige Funktionswerte
Yn(x) ::
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Argumente können groß sein:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Derivate beliebiger Ordnung, einschließlich negativer, können berechnet werden:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Modifizierte Bessel-Funktion der ersten Art
mpmath.besseli(n, x, derivative=0)
Besseli (n, x, Ableitung = 0) modifizierte Bessel-Funktion der ersten Art
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
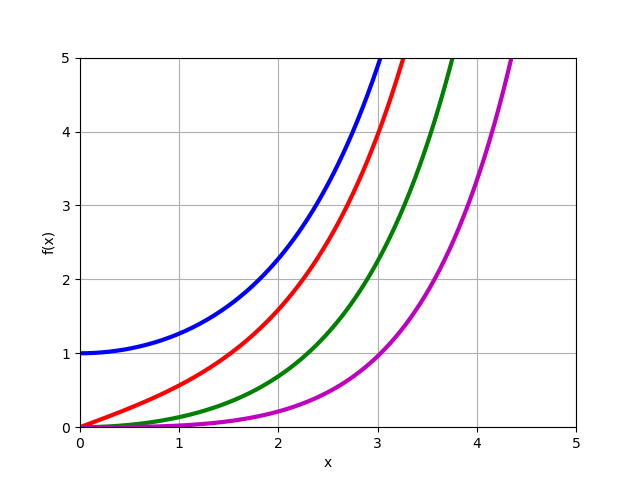
Modifizierte Bessel-Funktion
In(x) für echte Bestellungen
n=0,1,2,3 ::
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
Modifizierte Bessel-Funktion
In(x) in der komplexen Ebene
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Beispiele:
Einige Bedeutungen
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Argumente können groß sein:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Für ganze Zahlen n gilt die folgende ganzzahlige Darstellung:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Derivate beliebiger Ordnung können berechnet werden:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Modifizierte Bessel-Funktionen der zweiten Art,
mpmath.besselk(n, x)
besselk (n, x) modifizierte Bessel-Funktionen zweiter Art
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
Für eine ganze Zahl
n Diese Formel sollte als Grenze verstanden werden.
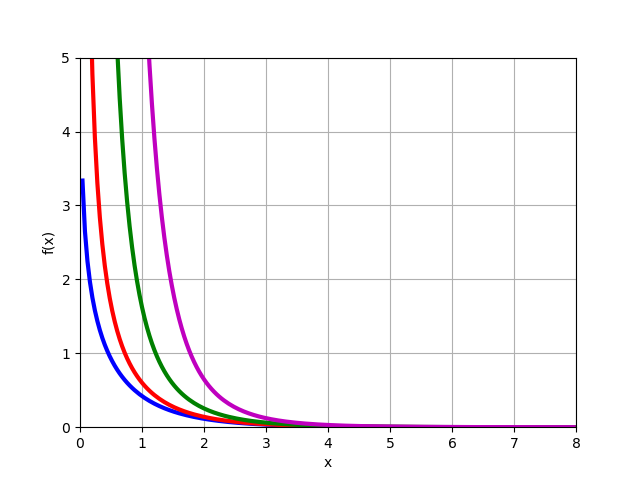
Modifizierte Bessel-Funktion der 2. Art
Kn(x) für Material
n=0,1,2,3 ::
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
Modifizierte Bessel-Funktion der 2. Art
Kn(x)) in der komplexen Ebene
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
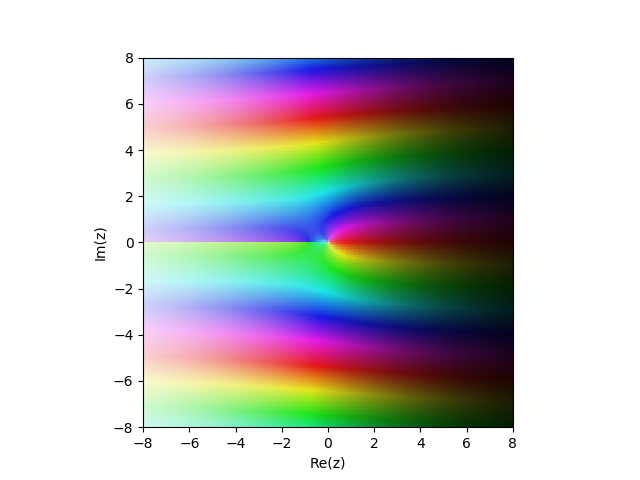
Beispiele:
Komplizierte und komplexe Argumente:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Argumente sind große Zahlen
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Merkmale des Verhaltens einer Funktion an einem Punkt
x=0 ::
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Bessel-Funktionsnullen besseljzero() mpmath.besseljzero(v, m, derivative=0)
Für echte Ordnung
mathit nu geq0 und eine positive ganze Zahl
m kehrt zurück
j nu,m , die m-te positive Null der Bessel-Funktion der ersten Art
J nu(z) (siehe
besselj () ). Alternativ mit
derivative=1 ergibt die erste nicht negative Primzahl Null
j′ nu,m von
J′ nu(z) . Indizierungsvereinbarungsbezeichnungen mit Abramowitz & Stegun und DLMF. Achten Sie auf einen Sonderfall.
j′0,1=0 während alle anderen Nullen positiv sind.
In der Realität werden nur einfache Nullen berechnet (alle Nullen der Bessel-Funktionen sind einfach, außer wenn
z=0 ) und
j nu,m wird eine monotone Funktion von
nu und
m . Nullen wechseln sich je nach Ungleichung ab:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
Beispiele:
Führende Nullen von Bessel-Funktionen
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Führende Nullen von Ableitungen von Bessel-Funktionen
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Nullen mit einem großen Index:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Nullen von Funktionen mit einer großen Bestellung:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Nullen von Funktionen mit gebrochener Ordnung:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
Und
J nu(z) . und
J′ nu(z) kann als unendliche Produkte an ihren Nullen ausgedrückt werden:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Für echte Ordnung
mathit nu geq0 und eine positive ganze Zahl
m kehrt zurück
y nu,m ,
m mth positive Null der zweiten Art der Bessel-Funktion
Y nu(z) (siehe
Bessely () ). Alternativ mit
derivative=1 gibt die erste positive Null
y′ nu,m von
Y′ nu(z) . Nullen wechseln sich je nach Ungleichung ab:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
Beispiele:
Führende Nullen von Bessel-Funktionen
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Führende Nullen von Ableitungen von Bessel-Funktionen
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Nullen mit einem großen Index:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Nullen von Funktionen mit einer großen Bestellung:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Nullen von Funktionen mit gebrochener Ordnung:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Bessel-FunktionsanwendungenDie Bedeutung von Bessel-Funktionen beruht nicht nur auf dem häufigen Auftreten der Bessel-Gleichung in Anwendungen, sondern auch auf der Tatsache, dass die Lösungen vieler anderer linearer Differentialgleichungen zweiter Ordnung in Form von Bessel-Funktionen ausgedrückt werden können. Um zu sehen, wie sie aussehen, beginnen wir mit der Bessel-Ordnungsgleichung
p in Form von:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
und hier ersetzen
w=x− alpha,z=kx beta,(2)
Verwenden Sie dann (2) und führen Sie die Konstanten ein
A,B,C aus Gleichung (1) erhalten wir:
x2y″+Axy′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)
Aus Gleichung (4) erhalten wir:
\ left \ {\ begin {matrix} \ alpha = \ frac {1-A} {2}, \\ \ beta = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C. }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right. (5)
Wenn
C>0 ,
q neq0 ,
(1−A)2 geqslant4B , dann die allgemeine Lösung (z
x>0 ) von Gleichung (3) hat die Form:
y(x)=x alpha left[c1Jp(kx beta)+c2J−p(kx beta) rechts](6)
wo:
alpha ,
beta ,
k werden aus System (5) bestimmt. Wenn
p Ist dann eine ganze Zahl
Jp müssen ersetzt werden durch
Yp .
Längsbiegung der vertikalen SäuleWir werden nun eine Aufgabe betrachten, die für praktische Anwendungen wichtig ist. Bei dieser Aufgabe muss bestimmt werden, wann eine gleichmäßige vertikale Säule unter ihrem eigenen Gewicht gebogen wird. Wir nehmen an
x=0 im freien oberen Ende der Spalte und
x=L>0 an seiner Basis; wir nehmen an, dass die Basis starr in die Basis (in den Boden) eingeführt (d. h. bewegungslos fixiert) ist, möglicherweise in Beton.

Bezeichnen Sie die Winkelabweichung der Säule am Punkt
x durch
theta(x) . Aus der Elastizitätstheorie unter diesen Bedingungen folgt:
EI fracd2 thetadx2+g rhox theta=0,(7)
wo
E - Elastizitätsmodul des Säulenmaterials,
I - Trägheitsmoment seines Querschnitts,
rho - lineare Dichte der Säule und
g - Gravitationsbeschleunigung. Die Randbedingungen haben folgende Form:
theta′(0)=0, theta(L)=0,(8)
Wir werden das Problem mit (7) und (8) lösen mit:
lambda= gamma2= fracg rhoEI(9)
Wir schreiben (7) unter Berücksichtigung von (9) unter Bedingung (8) neu:
fracd2 thetadx2+ gamma2x theta=0; fracd thetadx=0, theta(L)=0.(10)
Eine Säule kann nur verformt werden, wenn es eine nicht triviale Lösung für das Problem gibt (10); Andernfalls bleibt die Säule in einer Position, die nicht von der Vertikalen abweicht (d. h. physisch nicht in der Lage ist, von der Vertikalen abzuweichen).
Die Differentialgleichung (10) ist eine Airy-Gleichung. Gleichung (10) hat die Form von Gleichung (3) für
A=B=0 ,
C= gamma2 ,
q=3 . Aus dem Gleichungssystem (5) erhalten wir
alpha= frac12 ,
beta= frac32 ,
k= frac23 gamma ,
p= frac13 .
Daher hat die allgemeine Lösung die Form:
theta(x)=x1/2 left[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) right].(11)
Um die Anfangsbedingungen anzuwenden, ersetzen wir
p= pm frac13 in
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx2 right)2m+p(12)
Nach der Transformation (12) erhalten wir unter Berücksichtigung der Lösung (11):
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) left(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23) left(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right).(13)
Wird am Startpunkt bereitgestellt
theta′(0)=0 wir bekommen
c1=0 , dann nimmt (11) die Form an:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2),(14)
Wird am Endpunkt bereitgestellt
theta(L)=0 , aus (14) erhalten wir:
J−1/3( frac23 gammaL3/2)=0(15)
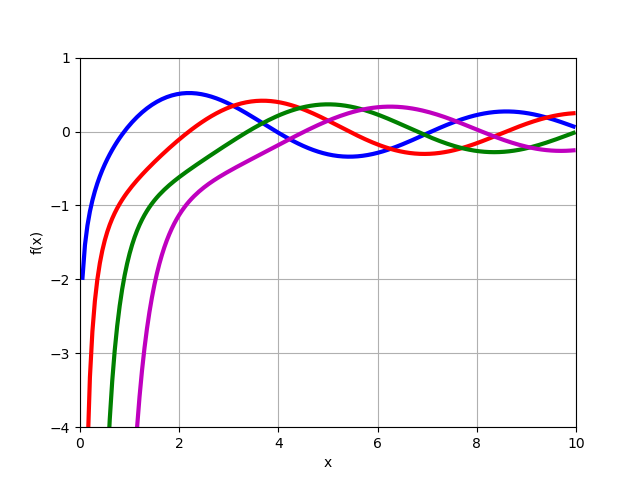
Es ist zu beachten, dass die Transformationen (13), (14) nicht durchgeführt werden könnten, wenn die Funktionsgraphen erstellt würden
J1/3(x),J−1/3(x) Verwenden der berücksichtigten Funktionen des mpmath-Moduls:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
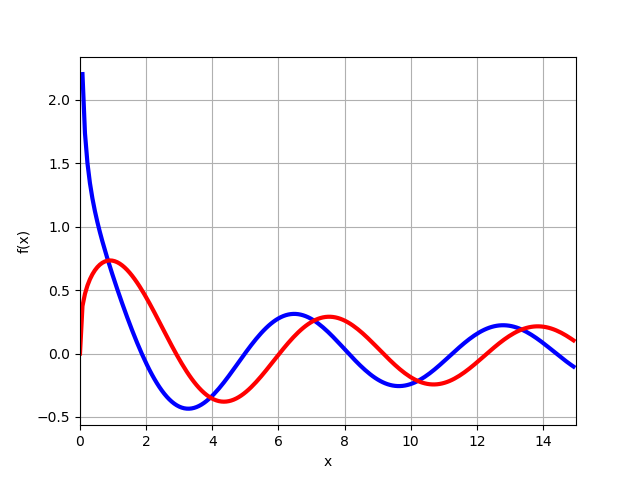
Aus dem Diagramm folgt, dass für x = 0 die Funktion ist
J1/3(0)=0 und unter Berücksichtigung der Lösung (11) erhalten wir sofort die notwendige Gleichung (15), es bleibt nur z zu finden, wie unten gezeigt wird.
Somit wird die Säule nur dann verformt, wenn
z= frac23 gammaL3/2 Ist die Wurzel der Gleichung
J−1/3(z)=0 . Erstellen Sie eine Funktion
J−1/3(z) auf einem separaten Diagramm:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

Die Grafik zeigt, dass die erste Wurzel etwas kleiner als 2 ist. Suchen Sie die Wurzel
z0 aus der Gleichung
J−1/3(z)=0 Mit der
Findroot-Funktion (f, z0) können Sie den
Suchpunkt gemäß der Grafik akzeptieren
x0=1 und sechs Dezimalstellen
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Wir bekommen:
z0=1,86635Wir berechnen die kritische Länge, zum Beispiel einen Fahnenmast, nach der Formel (15):
Fahnenmasthöhe für verschiedene Parameter im Abschnitt from numpy import* def LRr(R,r): E=2.9*10**11
Wir bekommen:
8,47 m
10,25 m
Ein hohler Fahnenmast kann höher sein als ein fester.
Wellenausbreitung in einer dünnen Membran.
Eine dünne Membran, wenn Schallwellen eintreten, schwingt nicht nur mit der Frequenz der Wellen. Die Form der Membranschwingungen kann in den Bessel-Funktionen gemäß der folgenden Auflistung unter Verwendung der Formeln
besselj () und
besseljzero () erhalten werden :
Membranwellenform from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()

Alternative zum mpmath-Modul in speziellen Bessel-Funktionen der SciPy-Bibliothek
Ohne auf eine detaillierte Diskussion der Bessel-Funktionen aus der SciPy-Bibliothek [4] einzugehen, werde ich nur zwei Auflistungen zum Zeichnen von Funktionen der ersten und zweiten Art
jv (v, x) ,
yv (v, x) geben :
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
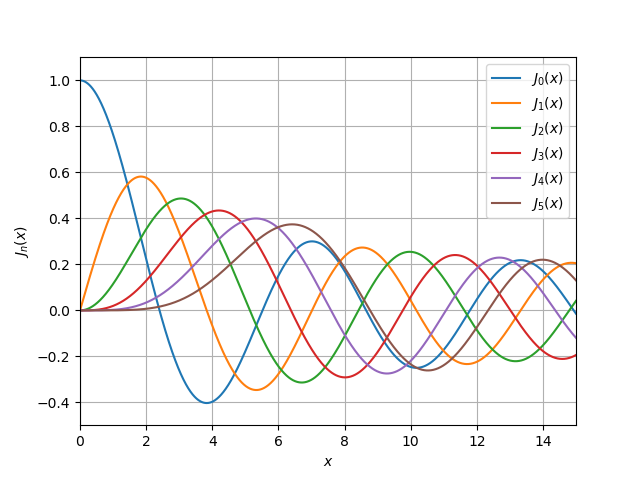
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()

Schlussfolgerungen:
Der Artikel beschreibt die Grundlagen der Arbeit mit Bessel-Funktionen unter Verwendung der Bibliotheken mpmath, sympy und scipy und enthält Beispiele für die Verwendung von Funktionen zum Lösen von Differentialgleichungen. Der Artikel kann nützlich sein, um die Gleichungen der mathematischen Physik zu studieren.
Referenzen:
1.
Bessel-Funktionen2.
Verwenden der inversen Laplace-Transformation zur Analyse der dynamischen Verknüpfungen von Steuerungssystemen3.
Bessel-funktionbezogene Funktionen4.
Sonderfunktionen (scipy.special).