Das Konvertieren von Modellen im laufenden Betrieb ist eine gängige Praxis bei der Simulation der Physik von Deformationen sowie bei Spielen mit dynamisch generierten und modifizierbaren Inhalten. In solchen Fällen ist es zweckmäßig, Methoden zum prozeduralen Bearbeiten und Erstellen von Geometrie anzuwenden. Letztere ermöglichen häufig das Speichern wertvoller Bytes beim Übertragen von aus dem Netzwerk heruntergeladenen Daten. Außerdem macht es Spaß!
Der Artikel zielt darauf ab, die Fähigkeiten der prozeduralen Verarbeitung von Netzen in Unity zu verbessern. Wir werden über die Operationen zum Transformieren und Generieren von Teilen eines Netzes sprechen.
Unser Gentleman-Kit für die prozedurale Bearbeitung von 3D-Modellen umfasst drei grundlegende Operationen: Triangulation, Bewegung von Punkten, Extrusion. Wir werden ausführlich über die letzten beiden sprechen. Betrachten Sie zunächst die einfachsten Bewegungsoperationen - Verschieben von Scheitelpunkten, Drehen und Skalieren von Kanten und Dreiecken. Dann werden wir uns mit einer der Methoden zum Erzeugen neuer Geometrie befassen - der Extrudieroperation.
In einer früheren Veröffentlichung haben wir unsere Struktur für die bequeme Arbeit mit Daten aus 3D-Modellen beschrieben.Strukturcodepublic static class CustomMeshPool { private static List<CustomMesh> Pool; private static int pointer; public static CustomMesh GetMesh(int id) { return Pool[id]; } public static int Push(CustomMesh customMesh) { if (Pool == null) Pool = new List<CustomMesh>(); pointer = GetAvailableIndex(); if (pointer < Pool.Count) Pool[pointer] = customMesh; else Pool.Add(customMesh); return pointer; } public static bool Remove(int index) { if (Pool == null) return false; var b = Pool[index] == null; Pool[index] = null; return b; } public static int GetAvailableIndex() { if (Pool == null) return 0; var availableIndex = Pool.FindIndex(mesh => mesh == null); return availableIndex != -1 ? availableIndex : Pool.Count; } public static void Flush() { if (Pool != null) Pool.Clear(); } } public class CustomMesh { public int Id; public Triangle[] Triangles; public Vector3[] vertices; public Vector3[] normals; public Vector2[] uv0, uv2; public Color[] colors; public CustomMesh(Vector3[] vertices, int[] triangles, Vector3[] normals, Vector2[] uv0, Vector2[] uv2, Color[] colors) { this.vertices = vertices; this.normals = normals; if (normals != null) for (var i = 0; i < this.normals.Length; i++) { this.normals[i] = this.normals[i].normalized; } this.uv0 = uv0; this.uv2 = uv2; this.colors = colors; var ptr = CustomMeshPool.GetAvailableIndex(); CustomMeshPool.Push(this); Id = ptr; Triangles = new Triangle[triangles.Length / 3]; Triangles = Triangles .AsParallel() .Select((t, i) => new Triangle(ptr, i, triangles[i * 3], triangles[i * 3 + 1], triangles[i * 3 + 2])) .ToArray(); } } public struct Triangle { private int _index; public int Index { get { return _index; } set { _index = value; if (_edges != null) { _edges[0].TriangleIndex = value; _edges[1].TriangleIndex = value; _edges[2].TriangleIndex = value; } } } private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private Edge[] _edges; public Edge[] Edges { get { return _edges; } set { if (value.Length == 3) { _edges = value; for (var i = 0; i < 3; i++) { _edges[i].TriangleIndex = _index; } } else throw new IndexOutOfRangeException(); } } public Vertex V0 { get { return Edges[0].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[0].v0 = value; Edges[2].v1 = value; } } public Vertex V1 { get { return Edges[1].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[1].v0 = value; Edges[0].v1 = value; } } public Vertex V2 { get { return Edges[2].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[2].v0 = value; Edges[1].v1 = value; } } public Triangle(int meshId, int index, int v0, int v1, int v2) { _index = index; _meshId = meshId; var edges = new Edge[3]; edges[0] = new Edge(meshId, index, v0, v1); edges[1] = new Edge(meshId, index, v1, v2); edges[2] = new Edge(meshId, index, v2, v0); _edges = edges; } } public struct Edge { public Vertex v0; public Vertex v1; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private int _triangleIndex; public int TriangleIndex { get { return _triangleIndex; } internal set { _triangleIndex = value; } } public Edge(int meshId, int triangleIndex, int v0Index, int v1Index) { _meshId = meshId; _triangleIndex = triangleIndex; v0 = new Vertex() { MeshId = meshId, Index = v0Index }; v1 = new Vertex() { MeshId = meshId, Index = v1Index }; } } public struct Vertex { public int Index; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } public Vector3 position { get { return CustomMeshPool.GetMesh(_meshId).vertices[Index]; } set { CustomMeshPool.GetMesh(_meshId).vertices[Index] = value; } } public Vector3 normal { get { return CustomMeshPool.GetMesh(_meshId).normals[Index]; } set { CustomMeshPool.GetMesh(_meshId).normals[Index] = value; } } public Vector2 uv0 { get { return CustomMeshPool.GetMesh(_meshId).uv0[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv0[Index] = value; } } public Vector2 uv2 { get { return CustomMeshPool.GetMesh(_meshId).uv2[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv2[Index] = value; } } public Color color { get { return CustomMeshPool.GetMesh(_meshId).colors[Index]; } set { CustomMeshPool.GetMesh(_meshId).colors[Index] = value; } } }
Wie Sie sehen können, wird hier PLINQ verwendet. Dies liegt daran, dass Algorithmen für die rechnerische Geometrie häufig durch Multithreading optimiert werden können.
Natürlich werden während der Ausführung von LINQ-Konstrukten mehr LINQ-Konstrukte erstellt als bei der Ausführung des „manuellen“ Codes. Dieser Nachteil wird jedoch weitgehend durch die Kürze solcher Entwürfe sowie das Vorhandensein integrierter Ressourcenmanagement-Tools in PLINQ ausgeglichen. Darüber hinaus wird der Übergang zwischen Single-Threaded- und Multi-Threaded-Implementierungen mit nur einem Befehl ausgeführt, was den Debugging-Prozess erheblich erleichtert.Ich verdrehe, verdrehe, ich möchte verwirren
Wir fahren mit den Operationen der Bewegung fort. Das Verschieben von Scheitelpunkten ist nicht kompliziert. Vergessen Sie nur nicht die zusammenfallenden Spitzen: Bei Bedarf sollte sich auch ihre Position ändern.
Der Algorithmus wird implementiert, indem der Scheitelpunktposition ein Bewegungsvektor hinzugefügt wird. Die Verschiebung erfolgt relativ zum Ursprung des Modells (
Pivot ). Es ist erwähnenswert, dass sich die Position von Polygonen während solcher Transformationen ändern kann, die Normalen ihrer Eckpunkte jedoch nicht. Um die Darstellung zu vereinfachen, werden wir diese Nuance jedoch nicht berücksichtigen.
CAD-Werkzeuge verfügen über eine Funktion zur Neuberechnung von Normalen, die normalerweise nach dem Anwenden der erforderlichen Transformationen aufgerufen wird. Es gibt verschiedene Möglichkeiten, diese Zuordnung vorzunehmen. Am häufigsten wird die Normale zur Ebene jedes Dreiecks berechnet und dann jedem Scheitelpunkt eine Normale als Durchschnitt der Normalen der Dreiecke zugewiesen, zu denen dieser Scheitelpunkt gehört.Im Allgemeinen gibt es keinen guten Grund, den Code zu komplizieren und die Transformationsmatrix anzuwenden. Das Ergebnis des Hinzufügens eines Bewegungsvektors zur Scheitelpunktposition entspricht einer intuitiven Vorstellung seiner Bewegung.
| 
|
Auflistungsmethoden zum Verschieben eines Scheitelpunkts public struct Vertex { ... public void Translate(Vector3 movement, bool withCoincident = false) { var newPosition = position + movement; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var mask = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(position); for (int i = 0; i < vertices.Length; i++) if (mask[i]) vertices[i] = newPosition; } else { position = newPosition; } } } public class CustomMesh { … public bool[] GetVerticesInPosition(Vector3 position) { bool[] buffer = new bool[vertices.Length]; for (int i = 0; i < buffer.Length; i++) { buffer[i] = Mathf.Abs(position.x - vertices[i].x) < Mathf.Epsilon && Mathf.Abs(position.y - vertices[i].y) < Mathf.Epsilon && Mathf.Abs(position.z - vertices[i].z) < Mathf.Epsilon; } return buffer; } }
Die Bewegung von Kanten und Dreiecken wird auf die gleiche Weise implementiert - durch Hinzufügen eines Verschiebungsvektors.
Auflistungsmethoden zum Verschieben von Dreiecken und Kanten public struct Edge { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var newV0Position = v0.position + movement; var newV1Position = v1.position + movement; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.Translate(movement); v1.Translate(movement); } } } public struct Triangle { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var newV0Position = V0.position + movement; var newV1Position = V1.position + movement; var newV2Position = V2.position + movement; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { V0.Translate(movement); V1.Translate(movement); V2.Translate(movement); } } }
Es ist jedoch bequemer, mithilfe
der Transformationsmatrix zu drehen und zu skalieren. Das Ergebnis der Ausführung dieser Operationen in Bezug auf den Ursprung der Modellkoordinaten entspricht höchstwahrscheinlich nicht Ihren Erwartungen oder Wünschen. Der Referenzpunkt für Rotation und Skalierung wird normalerweise als die Mitte des Objekts verwendet - als der für den Menschen verständlichste.
Auflistungsmethoden zum Drehen und Skalieren von Dreiecken und Kanten public struct Edge { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } } public struct Triangle { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(Vector3.zero, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(V0.position - pivot) + pivot; var newV1Position = matrix.MultiplyPoint(V1.position - pivot) + pivot; var newV2Position = matrix.MultiplyPoint(V2.position - pivot) + pivot; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } Edges[0].v0.normal = matrix.MultiplyPoint(V0.normal); Edges[1].v0.normal = matrix.MultiplyPoint(V1.normal); Edges[2].v0.normal = matrix.MultiplyPoint(V2.normal); } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(V0.position - pivot); var newV1Position = matrix.MultiplyPoint(V1.position - pivot); var newV2Position = matrix.MultiplyPoint(V2.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } } }
Schwärme ein ordentliches Loch für uns
Bei der 3D-Modellierung wird häufig eine Extrudieroperation verwendet. Für seine Implementierung müssen der Bewegungsvektor (Verschiebung) und die Menge der Polygone bekannt sein. Der Extrusionsprozess kann in zwei Schritte zerlegt werden:
1. Der Versatz der Polygone um einen bestimmten Bewegungsvektor (
Versatz ). In diesem Fall müssen die durch Grenzpolygone getrennten Scheitelpunkte dupliziert werden, um die Position der Elemente, die nicht zum verschobenen Teil gehören, nicht zu stören. Mit anderen Worten, Sie müssen das ausgewählte Stück zerreißen und bewegen. Wenn dieser Schritt zuerst abgeschlossen ist, wird das Modell wahrscheinlich in Teile zerfallen, die in Zukunft zusammengefügt werden müssen.
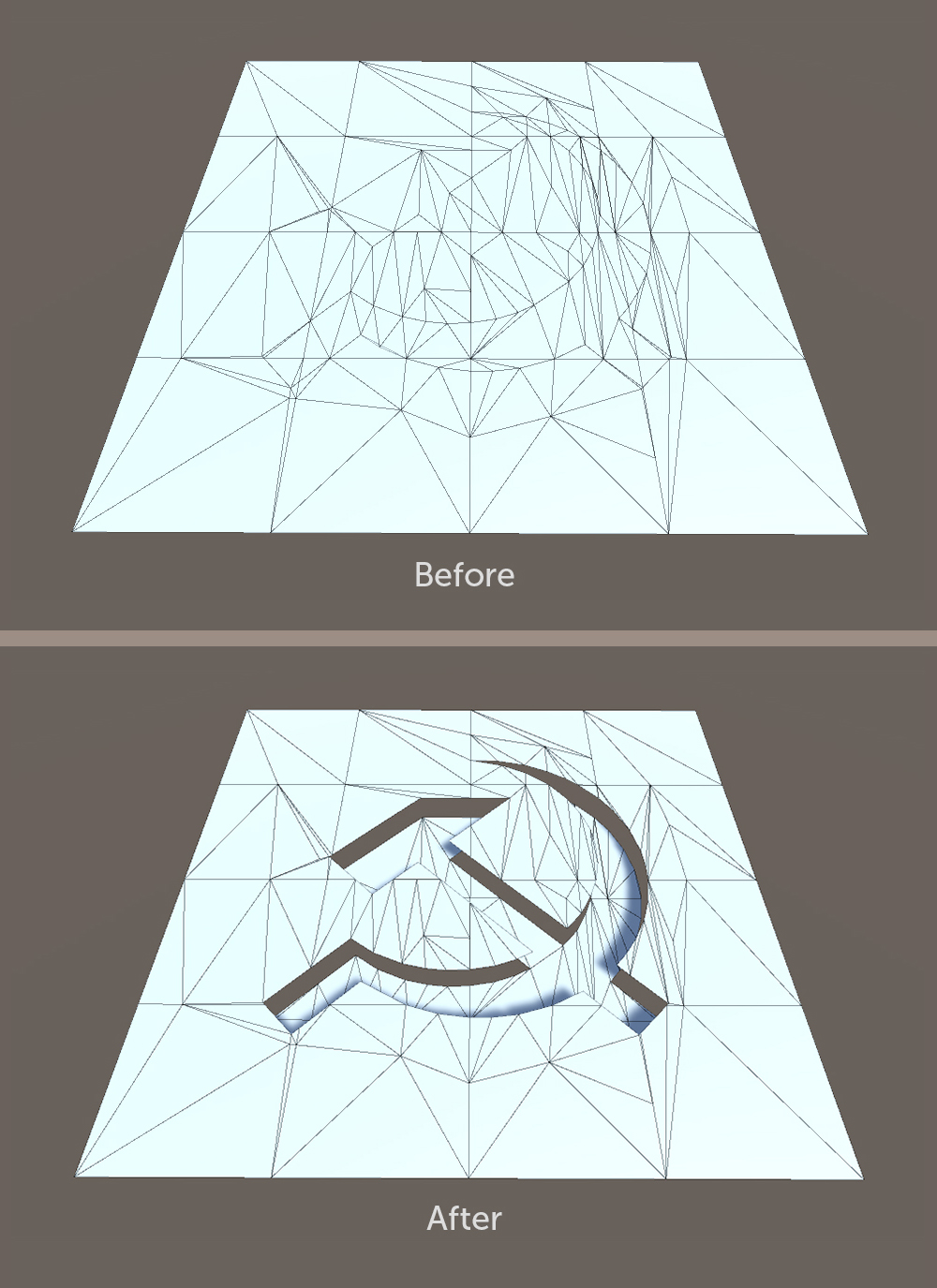
2. Hinzufügen einer neuen Geometrie zwischen der Grenze des versetzten Teils und der Grenze, die während der Extrusion gebildet wurde. Die Lücke zwischen dem Hauptteil und dem verschobenen Teil des Modells ist mit Polygonen gefüllt, die eine Wand bilden.
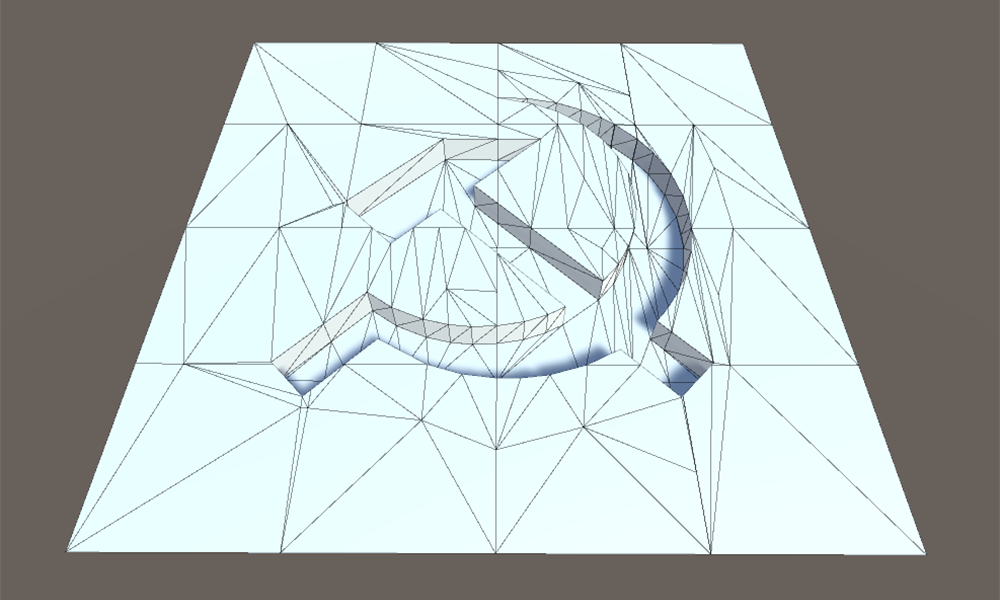
In der Implementierung ist es bequemer, zuerst die Wand zu bauen, da wir vor der Verschiebung die Anfangsposition der Kanten am Rand haben und diese Daten sofort verwenden können. Andernfalls müssten Sie entweder die Richtung des Schervektors invertieren oder einige Informationen über den Anfangszustand des Netzes speichern.
Das Modell und seine Teile, mit denen wir arbeiten, bestehen aus paarweise benachbarten Polygonen (Dreiecken). Wir nennen jede solche Menge einen
Cluster .
Zwei dedizierte Cluster in Blender
Zuerst müssen wir alle Kanten der Konturen erhalten, die die ausgewählten Cluster begrenzt haben. Fügen Sie dazu einfach die Kanten nacheinander zur Liste hinzu. Wenn eine passende Kante gefunden wird, muss diese entfernt werden, ohne die aktuelle hinzuzufügen. Für den korrekten Betrieb eines solchen Algorithmus muss eine Einschränkung eingeführt werden: Auf dem ausgewählten Satz von Dreiecken existieren nicht mehr als zwei zusammenfallende Kanten. In Fällen, in denen
Extrude verwendet wird, erfüllen Modelle häufig diese Bedingung, und ein komplexerer Algorithmus erfordert große Rechenressourcen.
Auflistungsmethoden zum Abrufen von Kanten, die zu Konturen gehören internal static class LinkedListExtension { internal static IEnumerable<LinkedListNode<T>> Nodes<T>(this LinkedList<T> list) { for (var node = list.First; node != null; node = node.Next) { yield return node; } } } public struct Vertex { … public bool IsInPosition(Vector3 other) { return Mathf.Abs(position.x - other.x) < Mathf.Epsilon && Mathf.Abs(position.y - other.y) < Mathf.Epsilon && Mathf.Abs(position.z - other.z) < Mathf.Epsilon; } } public struct Edge { … public bool Coincides(Edge other, bool includeDirection = false) { return v0.IsInPosition(other.v0.position) && v1.IsInPosition(other.v1.position) || !includeDirection && v1.IsInPosition(other.v0.position) && v0.IsInPosition(other.v1.position); } } public class CustomMesh { … private LinkedList<Edge> ObtainHullEdges(int[] triIndices) { var edges = new LinkedList<Edge>(); for (var i = 0; i < triIndices.Length; i++) { var edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[0])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[0]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[1])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[1]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[2])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[2]); } return edges; } }
Nachdem Sie alle Kanten der Kontur erhalten haben, müssen Sie die entsprechenden Wände erstellen. Es gibt viele Optionen für die Implementierung, aber wir haben uns für den Weg des geringsten Widerstands entschieden - Parallelogramme in Richtung des Bewegungsvektors basierend auf den Kanten separat zu erstellen. Da wir alle aufgrund dieser Aktion eine Verschiebung haben, bilden die Parallelogramme für jeden Cluster eine feste und geschlossene Wand. Es bleibt die Ausrichtung der Wandelemente zu bestimmen.
Die Wand besteht wie das gesamte Netz aus Dreiecken.
Gemäß der OpenGL- Konvention wird ein abgetrenntes Dreieck auf dem Bildschirm gerendert, wenn beim Projizieren seiner Punkte auf die Bildschirmebene die Umgehung dieser Punkte dem Gehen im Uhrzeigersinn entspricht:
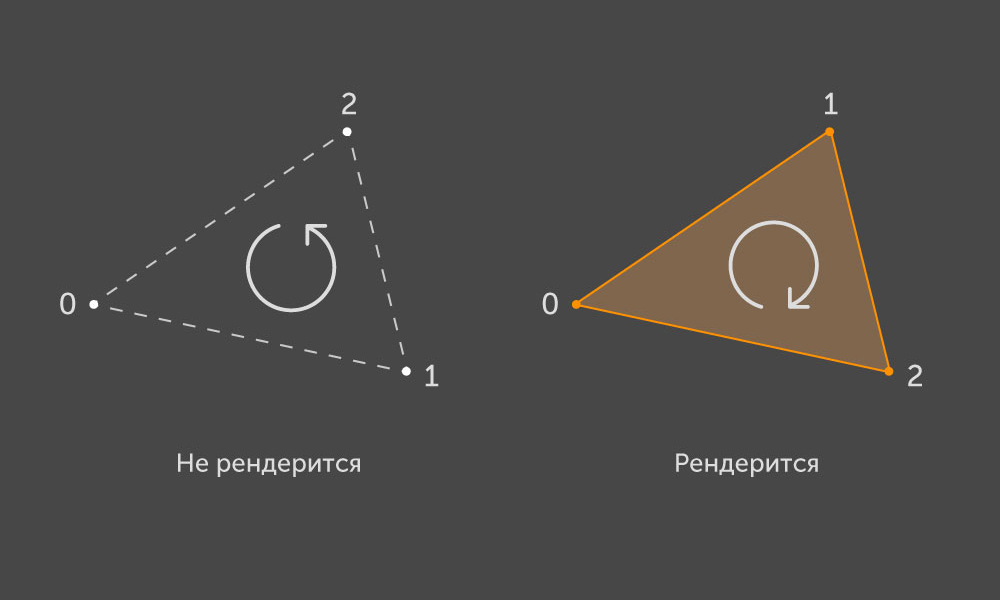
Ein Dreieck entspricht also einem bestimmten Normalenvektor, der die Vorderseite definiert. Jedes Dreieck wird von einer konvexen Kontur begrenzt, die aus drei Kanten besteht. Jede Kante hat zwei Eckpunkte, die in unserer Struktur als
v0 und
v1 dargestellt sind . Wir definieren die Richtung der Kante so, dass
v0 der Anfang ist,
v1 das Ende. Wenn nun die Richtung der Kanten des Dreiecks in Übereinstimmung mit der Umgehung seiner Eckpunkte festgelegt wird, muss jede Außenkontur des Clusters eine Umgehung entweder im oder gegen den Uhrzeigersinn und eine interne Umkehrung haben - umgekehrt. Wir haben
CustomMesh- und
Triangle- Konstruktoren implementiert, sodass die Durchquerung der Eckpunkte aller Dreiecke der Richtung im Uhrzeigersinn entspricht.
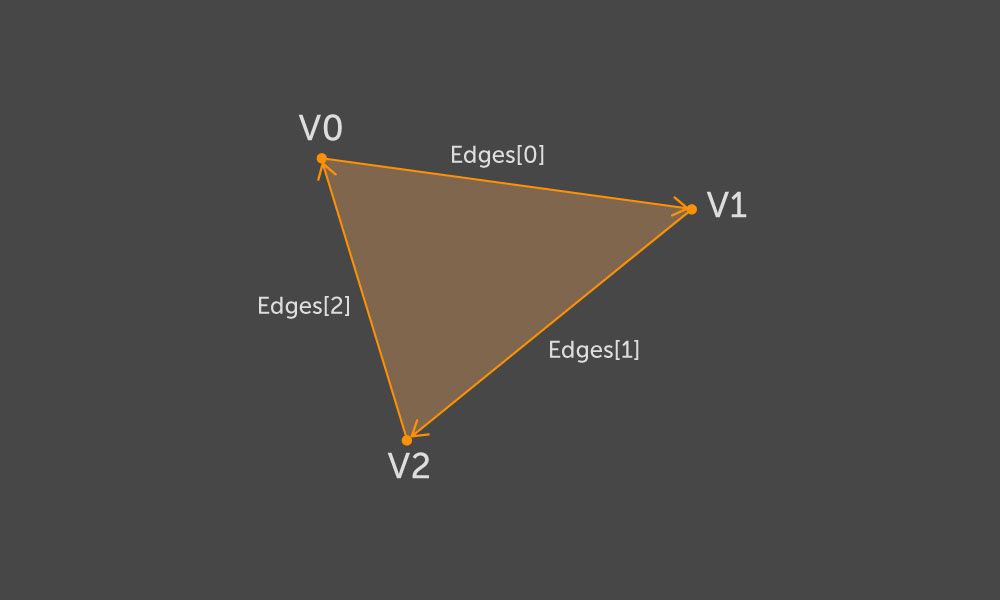
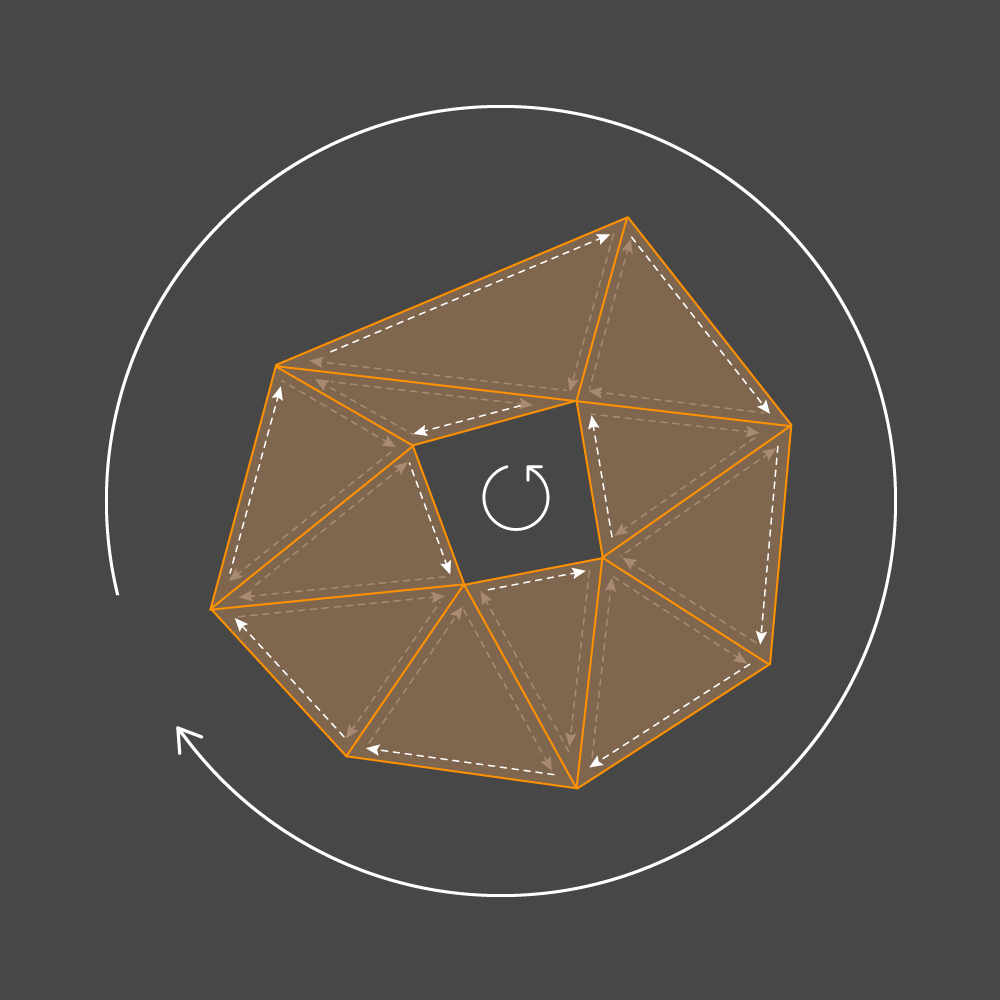
Mit der Richtung, die Kontur zu umgehen, können wir mit Sicherheit sagen, welche Seite der Rippe der innere Teil der Kontur und welche die äußere ist. Basierend auf diesen Informationen wählen wir die Ausrichtung der Wand. Sei (
v0, v1 ) die Kante, auf deren Grundlage das gewünschte Parallelogramm erzeugt werden soll. Wir nehmen die beiden Punkte
v2 und
v3 als Versatzpositionen
v0 und
v1 . Dann konstruieren wir zwei Dreiecke nach folgendem Schema:
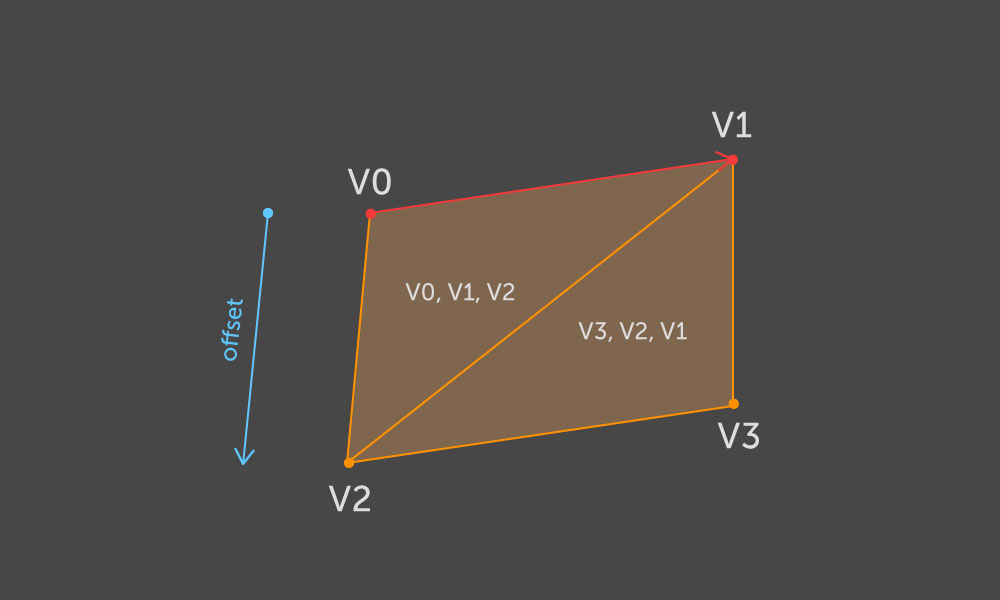
Und so für jede Kante der Kontur.
Auflisten einer Methode zum Erstellen von Wänden mithilfe einer Liste von Kanten public class CustomMesh { … private void ExtrudeEdgesSet(Edge[] edges, Vector3 offset) { if (offset == Vector3.zero || edges == null || edges.Length == 0) return; var initVerticesLength = vertices.Length; Array.Resize(ref vertices, initVerticesLength + edges.Length * 4); if (normals != null && normals.Length == initVerticesLength) { Array.Resize(ref normals, vertices.Length); } if (uv0 != null && uv0.Length == initVerticesLength) { Array.Resize(ref uv0, vertices.Length); } if (uv2 != null && uv2.Length == initVerticesLength) { Array.Resize(ref uv2, vertices.Length); } if (colors != null && colors.Length == initVerticesLength) { Array.Resize(ref colors, vertices.Length); } var initTrianglesLength = Triangles.Length; Array.Resize(ref Triangles, initTrianglesLength + edges.Length * 2); edges .AsParallel() .Select((edge, i) => { int j = initVerticesLength + i * 4; vertices[j] = edge.v0.position; vertices[j + 1] = edge.v1.position; vertices[j + 2] = edge.v0.position + offset; vertices[j + 3] = edge.v1.position + offset; if (normals != null && normals.Length == vertices.Length) { var normal = Vector3.Cross(vertices[j + 1] - vertices[j], offset); normals[j] = normals[j + 1] = normals[j + 2] = normals[j + 3] = normal; } if (uv0 != null && uv0.Length == vertices.Length) { uv0[j] = uv0[j + 2] = edge.v0.uv0; uv0[j + 1] = uv0[j + 3] = edge.v1.uv0; } if (uv2 != null && uv2.Length == vertices.Length) { uv2[j] = uv2[j + 2] = edge.v0.uv2; uv2[j + 1] = uv2[j + 3] = edge.v1.uv2; } if (colors != null && colors.Length == vertices.Length) { colors[j] = colors[j + 2] = edge.v0.color; colors[j + 1] = colors[j + 3] = edge.v1.color; } Triangles[initTrianglesLength + i * 2] = new Triangle( initTrianglesLength + i * 2, Id, j, j + 1, j + 2 ); Triangles[initTrianglesLength + i * 2 + 1] = new Triangle( initTrianglesLength + i * 2 + 1, Id, j + 3, j + 2, j + 1 ); return true; }).ToArray(); } }
Bei diesem Ansatz ist die Vorderseite der erzeugten Wände für die Objektträger und für die Gruben korrekt. Es gibt nur eine wesentliche Einschränkung: Der Satz von Dreiecken, über den die
Extrudieroperation ausgeführt wird, sollte in Bezug auf den Bewegungsvektor nicht um sich selbst gewickelt werden.
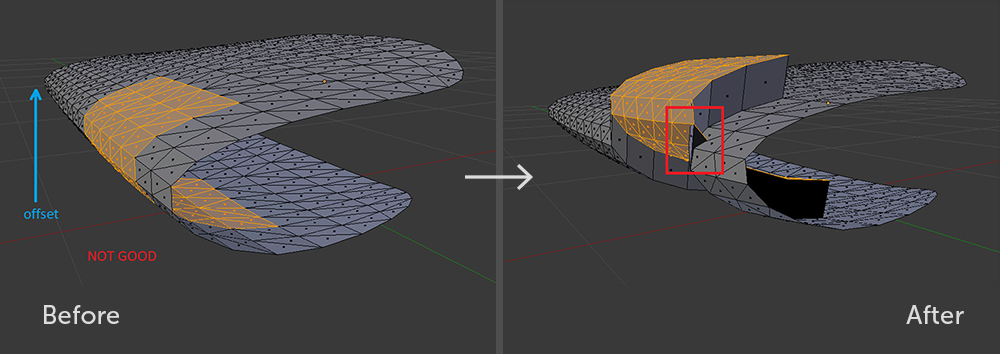Eine Teilmenge von Polygonen, die in Bezug auf den Versatz ungültig ist. Selbst in Blender mit einem solchen Extrudieren können Sie der Geometriekurve nicht entkommen.
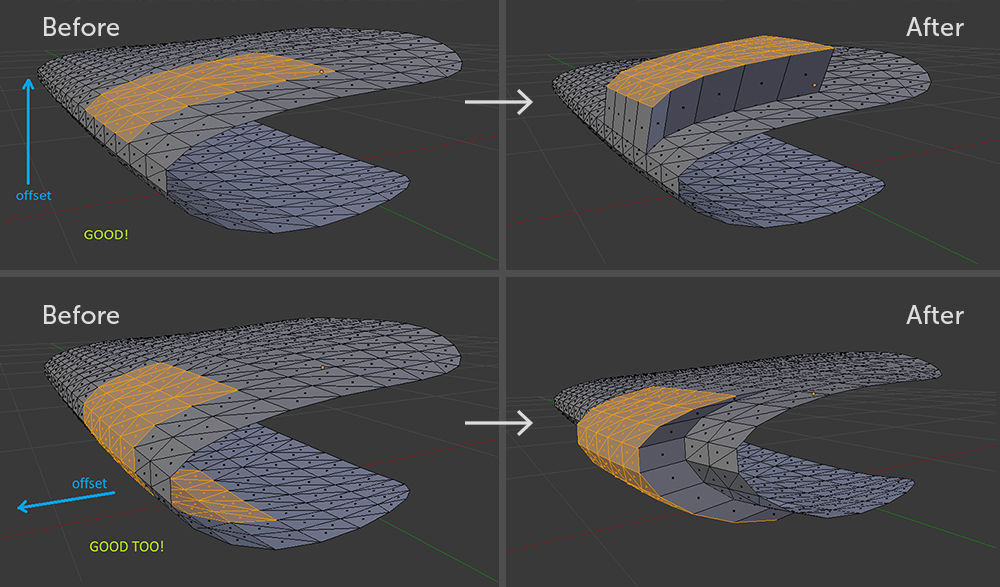Gültige Teilmengen von PolygonenDie Wand ist fertig, es bleibt, um die Dreiecke zu verschieben. Dieser Schritt des Algorithmus ist leicht zu verstehen, obwohl sich die Implementierung als umständlich herausstellte.
In unserem Fall müssen wir sicherstellen, dass jeder Scheitelpunkt des Clusters nur zu seinen Dreiecken gehört. Wenn die Bedingung nicht erfüllt ist, können einige benachbarte Polygone nach dem Cluster greifen. Die Lösung für diese Situation besteht darin, jeden Scheitelpunkt zu duplizieren, der sowohl zum Cluster als auch zum Rest des Modells gehört. Ersetzen Sie dann für alle Polygone im Cluster den Index dieses Scheitelpunkts durch den doppelten Index. Wenn die Bedingung erfüllt ist, verschieben wir alle Eckpunkte des Clusters zum Bewegungsvektor.
Auflisten einer Methode zum Verschieben eines Polygonclusters public class CustomMesh { … private void TranslateTrianglesHard(int[] triIndices, Vector3 offset, int[] hullVerts) { var newVertexIndices = new Dictionary<int, int>(); var initVerticesCount = vertices.Length; Triangles.Where((t, i) => !triIndices.Contains(i)).Select(t => { if (hullVerts.Contains(t.V0.Index) && !newVertexIndices.ContainsKey(t.V0.Index)) newVertexIndices.Add(t.V0.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V1.Index) && !newVertexIndices.ContainsKey(t.V1.Index)) newVertexIndices.Add(t.V1.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V2.Index) && !newVertexIndices.ContainsKey(t.V2.Index)) newVertexIndices.Add(t.V2.Index, initVerticesCount + newVertexIndices.Count); return false; }).ToArray(); Array.Resize(ref vertices, initVerticesCount + newVertexIndices.Count); foreach (var pair in newVertexIndices) vertices[pair.Value] = vertices[pair.Key] + offset; if (normals != null && normals.Length == initVerticesCount) { Array.Resize(ref normals, vertices.Length); foreach (var pair in newVertexIndices) normals[pair.Value] = normals[pair.Key]; } if (uv0 != null && uv0.Length == initVerticesCount) { Array.Resize(ref uv0, vertices.Length); foreach (var pair in newVertexIndices) uv0[pair.Value] = uv0[pair.Key]; } if (uv2 != null && uv2.Length == initVerticesCount) { Array.Resize(ref uv2, vertices.Length); foreach (var pair in newVertexIndices) uv2[pair.Value] = uv2[pair.Key]; } if (colors != null && colors.Length == initVerticesCount) { Array.Resize(ref colors, vertices.Length); foreach (var pair in newVertexIndices) colors[pair.Value] = colors[pair.Key]; } var alreadyMoved = new HashSet<int>(); for (var i = 0; i < triIndices.Length; i++) { if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V0.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V0.Index]; Triangles[triIndices[i]].Edges[0].v0.Index = index; Triangles[triIndices[i]].Edges[2].v1.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V0.Index)) { vertices[Triangles[triIndices[i]].V0.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V0.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V1.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V1.Index]; Triangles[triIndices[i]].Edges[0].v1.Index = index; Triangles[triIndices[i]].Edges[1].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V1.Index)) { vertices[Triangles[triIndices[i]].V1.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V1.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V2.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V2.Index]; Triangles[triIndices[i]].Edges[1].v1.Index = index; Triangles[triIndices[i]].Edges[2].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V2.Index)) { vertices[Triangles[triIndices[i]].V2.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V2.Index); } } } }
Fertig. Wenn wir nun die Ergebnisse aller Schritte addieren, erhalten wir ein Loch oder einen Hügel.
Auflisten der endgültigen Methode für die Extrudieroperation public class CustomMesh { … public void ExtrudeTriangles(int[] triIndices, Vector3 offset) { var edges = ObtainHullEdges(triIndices); ExtrudeEdgesSet(edges.ToArray(), offset); var hullVertices = edges.Select(edge => edge.v0.Index).ToArray(); TranslateTrianglesHard(triIndices, offset, hullVertices); } }
Wenn Sie mit den Koordinaten des Textur-Scans und der Verschiebung der Konturpunkte gespielt haben, können Sie eine solche Aussparung erhalten:
Und das ist noch nicht alles
Zusätzlich zu den oben beschriebenen Bearbeitungsvorgängen verwenden wir auch andere bequeme Methoden zum Arbeiten mit Modellen.
Zum Beispiel haben wir zusätzlich die
Combine () -Methode geschrieben, um zwei
CustomMesh zu kombinieren. Der Hauptunterschied zwischen unserer Implementierung und
UnityEngine.Mesh.CombineMeshes () besteht darin, dass, wenn einige Scheitelpunkte beim Kombinieren der Netze vollständig gleichwertig sind, nur einer davon
übrig bleibt, wodurch unnötige Geometrie vermieden wird.
Im selben Modul haben wir
den Delaunay-Ebenentriangulationsalgorithmus implementiert. Mit ihm können Sie beispielsweise ein großes Loch, das mit
Extrude erstellt wurde, mit einem flachen Deckel mit Wassertextur schließen und einen See erhalten:
Nun, habe es geklärt! Im nächsten Artikel werden die Funktionen zum Importieren von
.fbx in
Unity und die Methoden zur Modellvalidierung in einem Projekt behandelt.
Für einen Snack (nur für Lulz)