Entwicklung eines Hexapods von Grund auf neu (Teil 4) - mathematische Trajektorien und Sequenzen

Hallo allerseits! Die Hexapod-Entwicklung ist noch einen Schritt weiter gegangen. Dieses Mal werden die Trajektorien der Bewegung der Gliedmaßen implementiert und getestet - der nächste Teil der Bewegungsmathematik. In diesem Artikel werde ich über diese Trajektorien und grundlegenden Bewegungsabläufe sprechen. Ich hoffe es wird interessant.

Entwicklungsstadien:
Teil 1 - Design
Teil 2 - Montage
Teil 3 - Kinematik
Teil 4 - mathematische Trajektorien und Sequenzen
Teil 5 - Elektronik
Teil 6 - Übergang zum 3D-Druck
Teil 7 - Neues Gehäuse, Anwendungssoftware und Kommunikationsprotokolle

Flugbahnen

Das Wesentliche an diesem Mechanismus ist, dass Sie beim Setzen von zwei Punkten die Flugbahn der Extremität auswählen können. Beim Übergang von einem Punkt zum anderen ändern sich die Koordinaten gemäß bestimmten parametrischen Gleichungen. Der Mechanismus erwies sich als ziemlich leistungsfähig und ermöglicht es Ihnen, interessante Kurven für die Bewegung zu erhalten. Es implementiert auch eine Glättung von Bewegungen durch Ändern des Schritts des Parameters t - je kleiner der Schritt, desto mehr Zwischenpunkte gibt es, desto niedriger ist die Geschwindigkeit und desto glatter ist die Bewegung.

Das Verfahren zum Einstellen der Parameter der Flugbahn ist an einigen Stellen etwas unverständlich und kann verwirrt sein. Die Schwierigkeit liegt in der Tatsache, dass beim Festlegen der Koordinaten der Start- und Endpunkte die Koordinaten der realen Punkte im Raum nicht immer festgelegt werden, d. H. Einige Koordinaten legen die Trajektorienparameter fest. Ich musste ein Programm schreiben, das einen bestimmten Pfad anzeigt und gleichzeitig die Erreichbarkeit jedes Punkts des Pfads überprüft.

Der Treiber unterstützt die folgenden Bewegungspfade:

1. XYZ_LINAR ist die einfachste aller Trajektorien. Die Flugbahn wird verwendet, wenn Sie sich vorwärts, rückwärts, auf und ab bewegen. Alle Koordinaten ändern sich linear und werden wie folgt berechnet:
   
   

   x = t * (x1 - x0) / 180.0f + x0; y = t * (y1 - y0) / 180.0f + y0; z = t * (z1 - z0) / 180.0f + z0; 

   
   Hier verstehen wir, dass es keine Probleme gibt. Die Koordinaten geben die Parallelepipedwinkel an und stimmen mit den realen Koordinaten überein. Die Bewegung erfolgt entlang der Diagonale der Box.
   
   
   Trajektorienvisualisierung

   
   
   
   
   
   
2. YZ_ARC_Y_LINEAR - Mit dieser Trajektorie können Sie Bewegungen entlang eines Bogens implementieren. Die Flugbahn wird beim Wenden verwendet, wenn Sie ein Glied auf dem Boden bewegen müssen. Die Koordinaten werden wie folgt berechnet:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // Circle Y y = t * (y1 - y0) / 180.0f + y0; z = R * cos(t_mapped_rad); // Circle X 

   
   Hier beginnt der Spaß. Die Koordinaten geben die Richtung der Strahlen an, um den Bogen zu begrenzen, und sie stimmen möglicherweise nicht mit den tatsächlichen Koordinaten überein. Die Strahlen befinden sich in derselben Ebene, während der Radius des Kreises gleich der Länge des Vektors zum Startpunkt ist.
   
   
   Trajektorienvisualisierung

   
   
   
   
   
   
3. XZ_ARC_Y_SINUS - Mit dieser Trajektorie können Sie auch Bewegungen entlang eines Bogens implementieren, die jedoch komplexer sind als YZ_ARC_Y_LINEAR. Die Flugbahn wird beim Wenden verwendet, wenn Sie ein Glied durch die Luft bewegen müssen. Die Koordinaten werden wie folgt berechnet:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // circle Y y = (y1 - y0) * sin(DEG_TO_RAD(t)) + y0; z = R * cos(t_mapped_rad); // circle X 

   
   Der Spaß geht weiter. Die Koordinaten geben auch die Richtung der Strahlen an, um den Bogen zu begrenzen, stimmen jedoch NICHT mit den tatsächlichen Koordinaten überein. Die Y-Koordinate des Zielpunkts legt die Sinushöhe fest.
   
   
   Trajektorienvisualisierung

   
   
   
   
4. XZ_ELLIPTICAL_Y_SINUS - Mit dieser Trajektorie können Sie Bewegungen entlang einer Ellipse implementieren. Die Flugbahn wird verwendet, wenn Sie sich vorwärts und rückwärts bewegen, wenn Sie ein Glied durch die Luft bewegen müssen. Diese Flugbahn ist eine Komplikation von XZ_ARC_Y_SINUS und wurde nur wegen des visuell hässlichen Gangs bei Verwendung von XZ_ARC_Y_SINUS benötigt (Beine zu stark gestreckt). Die Koordinaten werden wie folgt berechnet:
   
   

    float a = (z1 - z0) / 2.0f; float b = (x1 - x0); float c = (y1 - y0); x = b * sin(DEG_TO_RAD(180.0f - t)) + x0; // circle Y y = c * sin(DEG_TO_RAD(t)) + y0; z = a * cos(DEG_TO_RAD(180.0f - t)) + z0 + a; 

   
   Die Koordinaten geben die Parallelepipedwinkel an und stimmen NICHT mit den realen Koordinaten überein. Die Bewegung erfolgt von den unteren Ecken des Kastens aus, die sich in derselben Ebene befinden wie das Berühren der Oberseite seines Teils. Es ist besser, sich das Bild im Spoiler anzusehen, ich weiß nicht, wie ich es kurz in Worten beschreiben soll.
   
   
   Trajektorienvisualisierung

   
   

Dies vervollständigt die grundlegende Mathematik der Bewegung des Hexapods. In meinem Projekt ist dies ein notwendiges Minimum für die Umsetzung fast jeder Bewegung.

Sequenzen

Ein bisschen Theorie

Sequenzen sind die elementaren Aktionen, aus denen sich der Gang zusammensetzt. Sie sind in zyklische und nichtzyklische unterteilt.

• Zyklische Sequenzen können viele Male ausgeführt werden und sollten am Ende jedes Zyklus die Gliedmaßen in ihre ursprüngliche Position zurückbringen (Bewegung und Drehung);
• Nichtzyklische Sequenzen werden nur einmal durchgeführt (Auf- und Abstieg);

Jede Sequenz hat drei Iterationsblöcke: Vorbereitungsblock, Hauptblock, Abschlussblock.

• Trainingsblock - enthält Iterationen, um die Gliedmaßen in die Ausgangsposition für die Sequenz zu bewegen. In meinem Fall erfordert das Vorwärtsbewegen, dass Sie Ihre Beine in eine bestimmte Position bringen, bevor Sie sich bewegen. Es wird einmal beim Übergang zur Sequenz ausgeführt;
• Hauptblock - enthält die Hauptiteration der Sequenz. Es kann zyklisch durchgeführt werden;
• Blockvervollständigung - enthält Iterationen zum Bewegen der Gliedmaßen in die Basisposition (die Position, in der die Gliedmaßen nach dem Anheben eingestellt werden);

Die folgende Abbildung zeigt die Reihenfolge für das Vorwärtsbewegen.

• Rote Punkte zeigen die Ausgangsposition der Gliedmaßen an, bevor sie sich bewegen
• Blaue Linien zeigen die Flugbahnen der Extremität am Boden an
• Die schwarzen Linien zeigen die Flugbahnen des Gliedes in der Luft an
• Die Pfeile geben die Reihenfolge an

Die Koordinaten der Punkte werden basierend auf der Konfiguration des Gehäuses ausgewählt. Ich habe die Punkte so nah wie möglich am Körper gewählt, um die Länge des Hebels zu verringern. In einem Zyklus der Sequenz bewegt sich der Hexapod um 18 cm (in 1 Zyklus werden 2 Schritte ausgeführt - 1 Schritt in 3 Gliedmaßen). Wenn Sie den Abstand vergrößern, klammern sich die Gliedmaßen aneinander. Dieser Parameter ist nur durch die Fallkonfiguration begrenzt.


Die Sequenz wird durch zwei Punkte (1, 2) für jedes Glied definiert und zwei Pfade werden verwendet: XYZ_LINEAR (blaue Linien) und XZ_ELLIPTICAL_Y_SINUS (schwarze Linien). Punkt 1 wird von der XZ_ELLIPTICAL_Y_SINUS-Trajektorie verwendet, um die Sinushöhe und dementsprechend die Höhe festzulegen, auf die der Fuß steigt. Die Punkte 2 und 3 sind echte Punkte, die ein Glied beim Bewegen erreicht.

Die Position der Punkte hängt nur von Ihrer Vorstellungskraft und den Fähigkeiten des Hexapods ab. Vielleicht hat sich alles als etwas kompliziert herausgestellt und es gibt eine einfachere Option, aber anscheinend habe ich sie noch nicht erreicht.

Implementierung

Schauen wir uns nun die Umsetzung all dieses Glücks an. Strukturen mit Sequenzparametern sind wie folgt:

 typedef struct { point_3d_t point_list[SUPPORT_LIMB_COUNT]; path_type_t path_list[SUPPORT_LIMB_COUNT]; uint32_t smooth_point_count; } sequence_iteration_t; typedef struct { bool is_sequence_looped; uint32_t main_sequence_begin; uint32_t finalize_sequence_begin; uint32_t total_iteration_count; sequence_iteration_t iteration_list[15]; sequence_id_t available_sequences[SUPPORT_SEQUENCE_COUNT]; } sequence_info_t; 

sequence_iteration_t - enthält Informationen zur Iteration der Sequenz:

• point_list - ein Array von Punkten für jedes Glied im XYZ-Format;
• path_list - ein Array von Trajektorien für jedes Glied;
• ooth_point_count - legt die Anzahl der Pfadpunkte fest (Parameterschritt t);

sequence_info_t - enthält Informationen zur gesamten Sequenz:

• is_sequence_looped - legt den Sequenztyp fest: zyklisch oder nicht;
• main_sequence_begin - legt den Startindex des Hauptblocks im Array iteration_list fest;
• finalize_sequence_begin - legt den Startindex des Abschlussblocks im Array iteration_list fest;
• total_iteration_count - Legt die Anzahl der Iterationen in der Sequenz fest.
• iteration_list - ein Array von Iterationen;
• available_sequences - Legt die Liste der Sequenzen fest, die für den Übergang von der aktuellen Sequenz verfügbar sind (z. B. können wir nicht mit dem Gehen beginnen, ohne zuerst vom Boden aufzustehen).

HINWEIS: Der Index des Vorbereitungsblocks wird nicht absichtlich angegeben, sondern befindet sich immer am Anfang des Iterationsarrays.

Leider kann ich hier keinen Code zur Bestimmung der Reihenfolge angeben, da es ist ziemlich breit und sieht nach Transfers schrecklich aus. Ich hinterlasse hier nur einen Link zur Definitionsdatei .

Bewegungsverarbeitungsschema

Es lohnt sich, alle Höllenkreise zu erkennen, die die Sequenz zur Laufzeit durchläuft. Das Verarbeitungsschema ist wie folgt:

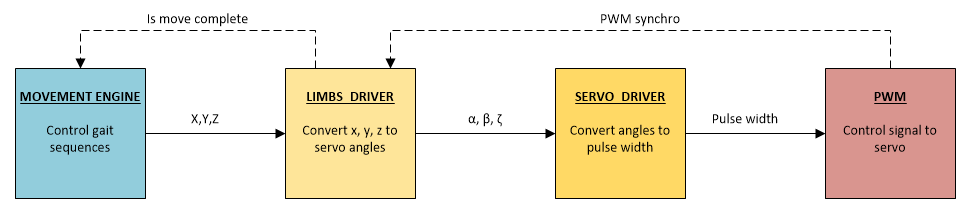
1. MOVEMENT ENGINE - organisiert die Verarbeitung und das Umschalten zwischen Sequenzen. Dort werden keine Berechnungen durchgeführt. Wenn vereinfacht, verschiebt dieses Modul den nächsten Punkt zum LIBMS DRIVER-Modul, nachdem die aktuelle Verarbeitung abgeschlossen ist.
   Moduleingabe: Array von Koordinaten der Zielpunkte.
   Modulausgabe: Zielpunkt für die aktuelle Iteration der Sequenz.
2. LIBMS DRIVER ist das komplexeste aller Module. Hier herrscht die gesamte Bewegungsmathematik: inverse Kinematik, Flugbahnberechnungen und Glättung von Bewegungen. Dieses Modul ist streng mit dem PWM-Modul synchronisiert. Die Berechnungen werden mit einer Frequenz von jeweils 150 Hz durchgeführt, der Steuerimpuls zu den Antrieben wird ebenfalls mit einer Frequenz von 150 Hz geliefert.
   Moduleingabe: Koordinaten des Zielpunktes.
   Modulausgang: Servodrehwinkel.
3. SERVO-FAHRER . Es gibt nichts Besonderes, außer einer Reihe von Parametern zum Einrichten und Einstellen von Laufwerken.
   Moduleingang: Servodrehwinkel.
   Modulausgang: Steuerimpulsbreite.
4. PWM-TREIBER . PWM-Treibersoftware zur Laufwerkssteuerung. Hier zucken die Stifte nur zur richtigen Zeit. Die PWM-Synchronisationssynchronisationsvariable wird in jeder PWM-Periode inkrementiert.
   Moduleingang: Steuerimpulsbreite.
   Modulausgang: Impulse an Steuerpins.

Ich habe versucht, die Module unabhängig voneinander zu machen, und es ist mir gelungen. Auf diese Weise können Sie jedes Zwischenmodul (z. B. das Anpassungsmodul an die Landschaft) in diese Schaltung einfügen, und gleichzeitig wird nichts unterbrochen, während die Implementierung mit minimalen Änderungen im Code erfolgt.

Neueste Nachrichten und Projektkrebse gefunden