Eine urbane Legende besagt, dass der Schöpfer von Zuckersäcken, Stöcken, sich erhängt hat, als er erfuhr, dass die Verbraucher sie nicht über eine Tasse in zwei Hälften zerbrechen, sondern die Spitze vorsichtig abreißen. Dies ist natürlich nicht der Fall, aber wenn diese Logik befolgt wird, sollte sich ein britischer Guinness-Bierliebhaber namens William Gosset nicht nur erhängen, sondern durch seine Rotation im Sarg die Erde bereits bis ins Zentrum bohren. Und das alles, weil seine ikonische Erfindung, die unter dem Pseudonym Student veröffentlicht wurde , seit Jahrzehnten katastrophal missbraucht wird.
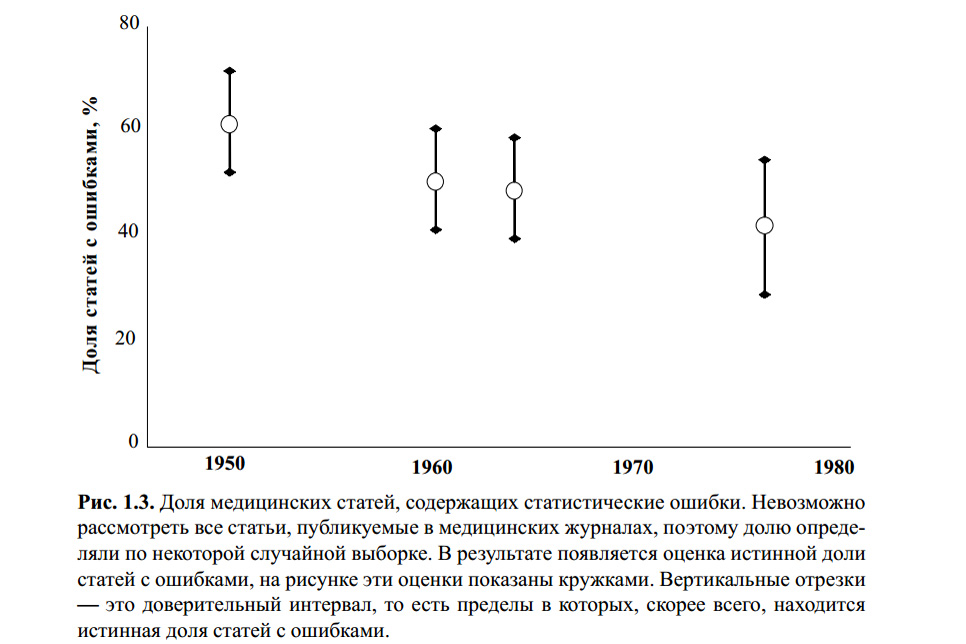
Die obige Abbildung stammt aus dem Buch von S. Glanz. Biomedizinische Statistik. Per. aus dem Englischen - M., Practice, 1998 - 459 p. Ich weiß nicht, ob jemand die Berechnungen für dieses Diagramm auf statistische Fehler überprüft hat. Eine Reihe moderner Artikel zu diesem Thema und meine eigenen Erfahrungen zeigen jedoch, dass das Student-T-Kriterium mit oder ohne das bekannteste und daher am häufigsten verwendete Kriterium bleibt.
Der Grund dafür ist oberflächliche Bildung (strenge Lehrer lehren, dass Sie "Statistiken überprüfen" müssen, sonst uuuuuu!), Benutzerfreundlichkeit (Tabellen und Online-Rechner sind in Hülle und Fülle verfügbar) und eine banale Zurückhaltung, sich mit der Tatsache zu befassen, dass "und so funktioniert es". Die meisten Leute, die dieses Kriterium mindestens einmal in ihrer Hausarbeit oder sogar in ihrer wissenschaftlichen Arbeit verwendet haben, werden etwas sagen wie: "Nun, wir haben 5 verärgerte Schulkinder und 7 Schulkinder-Spieler in Bezug auf Aggression verglichen, unser Tabellenwert liegt nahe bei p = 0,05 und das bedeutet, dass Spiele böse sind. Nun ja, nicht genau, aber mit einer Wahrscheinlichkeit von 95%. " Wie viele logische und methodische Fehler haben sie gemacht?
Die Grundlagen
Worauf basiert der Student T-Test? Die Logik ist dem Bayes'schen Theorem entnommen, die mathematische Grundlage ist die Gaußsche Verteilung, die Methodik basiert auf der Varianzanalyse:

Dabei ist der Parameter μ die mathematische Erwartung (Durchschnittswert) der Verteilung und der Parameter σ die Standardabweichung (σ² ist die Varianz) der Verteilung.
Was ist eine Varianzanalyse? Stellen Sie sich ein Habr-Publikum vor, sortiert nach der Anzahl der Personen eines bestimmten Alters. Die Anzahl der Personen nach Alter entspricht wahrscheinlich der Normalverteilung - gemäß der Gauß-Funktion:
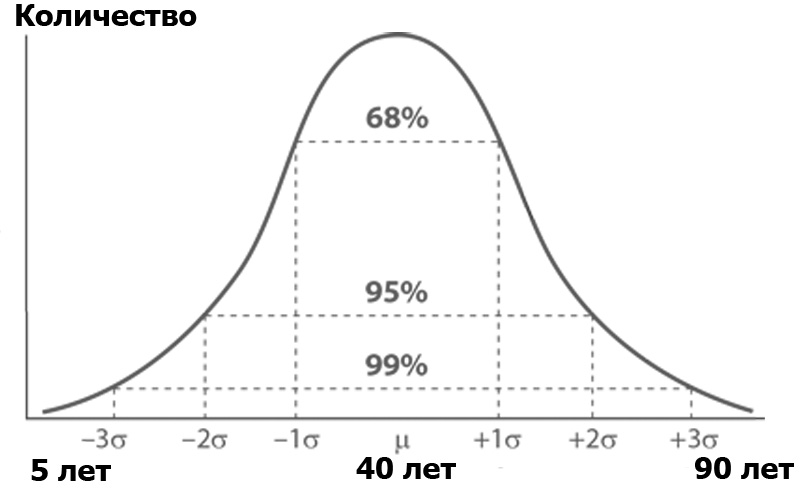
Die Normalverteilung hat eine interessante Eigenschaft - fast alle ihre Werte liegen in der Grenze von drei Standardabweichungen vom Durchschnittswert. Und was ist die Standardabweichung? Dies ist die Wurzel der Varianz. Die Streuung ist wiederum die Summe der Quadrate der Differenz aller Mitglieder der Allgemeinbevölkerung und des Durchschnittswerts geteilt durch die Anzahl dieser Mitglieder:
Das heißt, jeder Wert wurde vom Durchschnitt abgezogen, quadriert, um die Minuspunkte zu töten, und dann der Durchschnitt genommen, dumm zusammengefasst und durch die Anzahl dieser Werte geteilt. Das Ergebnis ist ein Maß für die durchschnittliche Streuung der Werte relativ zur Durchschnittsvarianz.
Stellen Sie sich vor, wir haben zwei Stichproben in dieser allgemeinen Population ausgewählt : Leser des Cryptocurrency-Hubs und Leser des Old Iron-Hubs. Durch die Erstellung einer Zufallsstichprobe erhalten wir immer Verteilungen, die nahezu normal sind . Und jetzt haben wir einen kleinen Händler in unserer Bevölkerung:
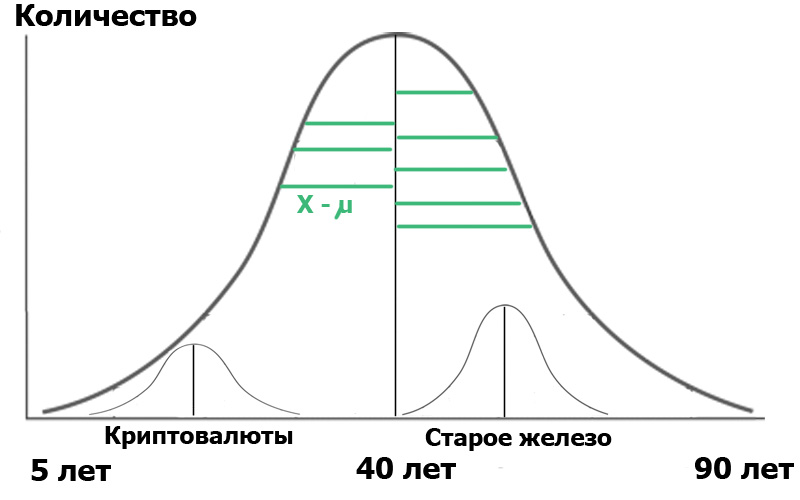
Zur Verdeutlichung habe ich grüne Segmente angezeigt - den Abstand zwischen den Verteilungspunkten und dem Durchschnittswert. Wenn die Längen dieser grünen Segmente quadriert, summiert und gemittelt werden, ist dies die Varianz.
Und jetzt - Aufmerksamkeit. Wir können die Population anhand dieser beiden kleinen Stichproben charakterisieren. Einerseits charakterisieren die Varianzen der Stichproben die Varianz der gesamten Population. Andererseits sind die Durchschnittswerte der Proben selbst auch Zahlen, für die die Varianz berechnet werden kann! Also: Wir haben den Durchschnitt der Varianzen der Stichproben und die Varianz der Durchschnittswerte der Stichproben.
Dann können wir eine Varianzanalyse durchführen und diese grob in Form einer logischen Formel darstellen:
Was gibt uns die obige Formel? Sehr einfach. In der Statistik beginnt alles mit der „Nullhypothese“, die formuliert werden kann als „es schien uns“, „alle Zufälle sind zufällig“ - in der Bedeutung und „es gibt keinen Zusammenhang zwischen den beiden beobachteten Ereignissen“ - wenn streng. In unserem Fall wäre die Nullhypothese das Fehlen signifikanter Unterschiede zwischen der Altersverteilung unserer Benutzer in zwei Hubs. Im Fall der Nullhypothese sieht unser Diagramm ungefähr so aus:
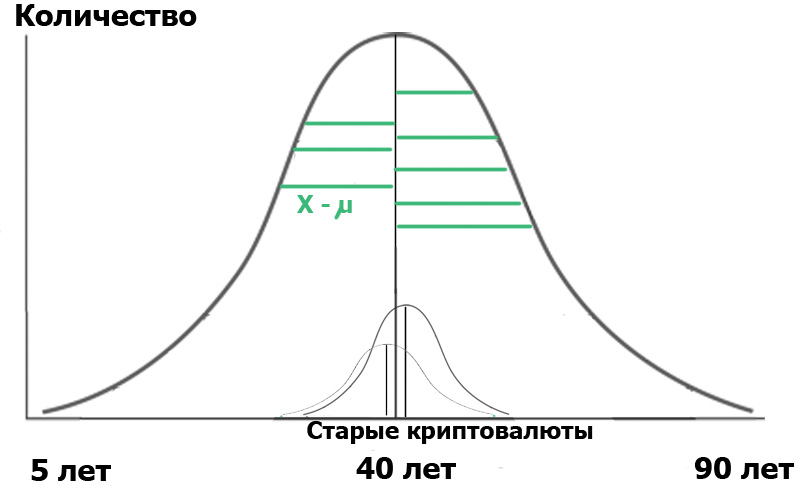
Dies bedeutet, dass sowohl die Varianzen der Stichproben als auch ihre Durchschnittswerte sehr nahe beieinander liegen und daher ganz allgemein unser Kriterium sind
Aber wenn die Varianzen der Stichproben gleich sind, aber das Alter der Habrauser wirklich sehr unterschiedlich ist, ist der Zähler (Varianz der Durchschnittswerte) groß und F ist viel mehr als eins. Dann sieht das Diagramm eher wie in der vorherigen Abbildung aus. Und was wird es uns geben? Nichts, wenn Sie den Wortlaut nicht beachten: Die Nullhypothese wäre das Fehlen signifikanter Unterschiede.
Aber die Bedeutung ... wir setzen sie selbst. Es wird als α bezeichnet und hat folgende Bedeutung: Das Signifikanzniveau ist die maximal akzeptable Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen . Mit anderen Worten, wir werden unser Ereignis nur dann als signifikanten Unterschied zwischen einer Gruppe und einer anderen betrachten, wenn die Wahrscheinlichkeit P unseres Fehlers kleiner als α ist. Dies ist der berüchtigte p <0,05, da in der biomedizinischen Forschung das Signifikanzniveau normalerweise auf 5% festgelegt wird.
Dann ist alles einfach. Abhängig von α gibt es kritische Werte für F, beginnend mit denen wir die Nullhypothese ablehnen. Sie werden in Form von Tabellen ausgegeben, die wir so gewohnt sind. Dies dient zur Varianzanalyse. Und was ist mit dem Studenten?
So sagte der Student
Und das Schülerkriterium ist nur ein Sonderfall der Varianzanalyse. Auch hier werde ich Sie nicht mit Formeln überladen, die leicht zu googeln sind, aber ich werde die Essenz vermitteln:
Diese lange Erklärung musste also sehr unhöflich und fließend sein, aber deutlich zeigen, worauf das t-Kriterium basiert. Und dementsprechend folgen aus seinen inhärenten Eigenschaften direkt die Einschränkungen seiner Verwendung, bei denen selbst professionelle Wissenschaftler so oft Fehler machen.
Eigenschaft Eins: Normalität der Verteilung.
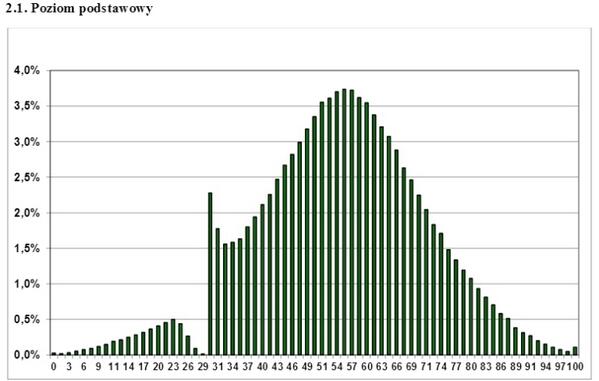
Dies ist ein paar Jahre als Grafik der Verteilung der polnischen Staatsexamen im Internet. Welche Schlussfolgerung kann daraus gezogen werden? Dass diese Prüfung nicht nur vollständig abgestoßener Gopnik bestanden wird? Welche Lehrer "erreichen" Schüler? Nein, nur eine - auf eine andere Verteilung als normal können Sie keine parametrischen Analysekriterien wie Student anwenden. Wenn Sie ein einseitiges, gezacktes, welliges, diskretes Verteilungsdiagramm haben - vergessen Sie das t-Kriterium, Sie können es nicht verwenden. Dies wird jedoch manchmal selbst bei ernsthaften wissenschaftlichen Arbeiten erfolgreich ignoriert.
Was ist in diesem Fall zu tun? Verwenden Sie die sogenannten nichtparametrischen Analysekriterien. Sie implementieren einen anderen Ansatz, nämlich die Rangfolge der Daten, dh die Abkehr von den Werten der einzelnen Punkte zu dem ihr zugewiesenen Rang. Diese Kriterien sind weniger genau als die parametrischen, aber zumindest ihre Verwendung ist korrekt, im Gegensatz zur ungerechtfertigten Verwendung des parametrischen Kriteriums bei einer abnormalen Population. Von diesen Kriterien ist das Mann-Whitney-U-Kriterium am besten bekannt und wird häufig als Kriterium "für eine kleine Stichprobe" verwendet. Ja, es ermöglicht Ihnen, mit Stichproben von bis zu 5 Punkten umzugehen, aber dies ist, wie bereits klar sein sollte, nicht der Hauptzweck.
Die zweite Eigenschaft: Erinnerst du dich an die Formel? Die Werte des F-Kriteriums änderten sich mit der Differenz (erhöhte Varianz) der Durchschnittswerte der Proben . Der Nenner, dh die Abweichungen selbst, sollten sich jedoch nicht ändern. Ein weiteres Kriterium für die Anwendbarkeit sollte daher die Gleichheit der Varianzen sein. Die Tatsache, dass diese Überprüfung noch seltener beobachtet wird, wird beispielsweise hier gesagt: Fehler bei der statistischen Analyse biomedizinischer Daten. Leonov V.P. Internationale Zeitschrift für medizinische Praxis, 2007, Nr. 2, S. 19-35 .
Eigenschaft Drei: Vergleich zweier Proben. Sie verwenden das t-Kriterium gerne, um mehr als zwei Gruppen zu vergleichen. Dies geschieht normalerweise wie folgt: Die Unterschiede zwischen Gruppe A von B, B von C und A von C. werden paarweise verglichen. Darauf aufbauend wird eine bestimmte Schlussfolgerung gezogen, die absolut falsch ist. In diesem Fall tritt der Effekt mehrerer Vergleiche auf.
Nachdem die Forscher in einem der drei Vergleiche einen ausreichend hohen Wert von t erhalten hatten, berichten sie, dass „P <0,05“. Tatsächlich liegt die Fehlerwahrscheinlichkeit jedoch deutlich über 5%.
Warum?
Wir finden es heraus: Zum Beispiel hat die Studie ein Signifikanzniveau von 5% angenommen. Dies bedeutet, dass die maximal akzeptable Wahrscheinlichkeit, die Nullhypothese beim Vergleich der Gruppen A und B fälschlicherweise abzulehnen, 5% beträgt. Es scheint, dass alles richtig ist? Der genau gleiche Fehler tritt jedoch beim Vergleich der Gruppen B und C und auch beim Vergleich der Gruppen A und C auf. Folglich beträgt die Wahrscheinlichkeit eines Fehlers bei dieser Art der Bewertung insgesamt nicht 5%, sondern viel mehr. Im Allgemeinen ist diese Wahrscheinlichkeit gleich
P '= 1 - (1 - 0,05) ^ k
Dabei ist k die Anzahl der Vergleiche.
In unserer Studie beträgt die Wahrscheinlichkeit, einen Fehler bei der Ablehnung der Nullhypothese zu machen, ungefähr 15%. Beim Vergleich der vier Gruppen beträgt die Anzahl der Paare und dementsprechend mögliche paarweise Vergleiche 6. Daher mit einem Signifikanzniveau in jedem der Vergleiche von 0,05
Die Wahrscheinlichkeit, versehentlich einen Unterschied in mindestens einem zu erkennen, beträgt nicht mehr 0,05, sondern 0,31.
Dieser Fehler ist jedoch nicht schwer zu beseitigen. Eine Möglichkeit ist die Einführung des Bonferroni-Änderungsantrags. Die Bonferroni-Ungleichung sagt uns, dass wenn Sie die Kriterien k-mal anwenden
mit einem Signifikanzniveau von α überschreitet die Wahrscheinlichkeit, in mindestens einem Fall einen Unterschied zu finden, wo er nicht existiert, das Produkt von k um α nicht. Von hier aus:
α '<αk,
wobei α 'die Wahrscheinlichkeit ist, die Unterschiede mindestens einmal zu verwechseln. Dann ist unser Problem ganz einfach gelöst: Wir müssen unser Signifikanzniveau durch die Bonferroni-Korrektur teilen, dh durch die Vielzahl der Vergleiche. Für drei Vergleiche müssen wir die Werte entsprechend α = 0,05 / 3 = 0,0167 aus den t-Testtabellen entnehmen. Ich wiederhole - es ist sehr einfach, aber dieser Änderungsantrag kann nicht ignoriert werden. Übrigens sollten Sie sich von dieser Änderung nicht mitreißen lassen, auch nach dem Teilen durch 8 sind die Werte des t-Kriteriums unnötig strenger.
Als nächstes kommen die "kleinen Dinge", die sie sehr oft überhaupt nicht bemerken. Ich gebe hier absichtlich keine Formeln an, um die Lesbarkeit des Textes nicht zu beeinträchtigen, aber es sollte beachtet werden, dass die Berechnungen des t-Kriteriums in den folgenden Fällen variieren:
Unterschiedliche Größen von zwei Stichproben (denken Sie im Allgemeinen daran, dass wir im allgemeinen Fall zwei Gruppen anhand der Formel für das Zwei-Stichproben-Kriterium vergleichen).
Verfügbarkeit abhängiger Proben. Dies sind Fälle, in denen Daten von einem Patienten in unterschiedlichen Zeitintervallen, Daten von einer Gruppe von Tieren vor und nach dem Experiment usw. gemessen werden.
Damit Sie sich das volle Ausmaß des Geschehens vorstellen können, werde ich abschließend neuere Daten zur falschen Verwendung des t-Kriteriums bereitstellen. Die Zahlen beziehen sich auf 1998 und 2008 für eine Reihe chinesischer wissenschaftlicher Zeitschriften und sprechen für sich. Ich möchte wirklich, dass sich dies als nachlässiger im Design herausstellt als ungenaue wissenschaftliche Daten:
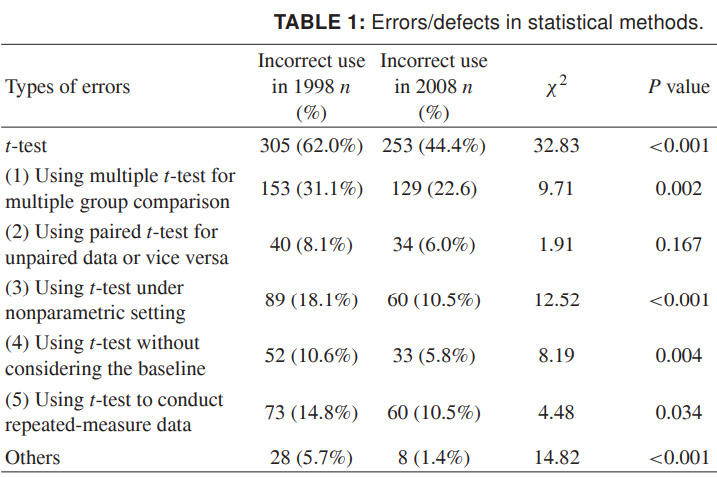
Quelle: Missbrauch statistischer Methoden in 10 führenden chinesischen medizinischen Fachzeitschriften in den Jahren 1998 und 2008. Shunquan Wu et al., The Scientific World Journal, 2011, 11, 2106–2114
Denken Sie daran, dass die geringe Bedeutung der Ergebnisse keine so traurige Sache wie ein falsches Ergebnis ist. Es ist unmöglich, zu wissenschaftlichen Sünden zu gelangen - falsche Schlussfolgerungen -, indem Daten mit falsch angewandten Statistiken verzerrt werden.
Über die logische Interpretation, einschließlich falscher, statistischer Daten, werde ich vielleicht separat berichten.
Lies es richtig.