In der Regel werden Änderungen an Algorithmen, die auf den spezifischen Merkmalen einer bestimmten Aufgabe beruhen, als weniger wertvoll angesehen, da sie sich nur schwer auf eine breitere Klasse von Problemen übertragen lassen. Dies bedeutet jedoch nicht, dass solche Änderungen nicht erforderlich sind. Darüber hinaus können sie häufig das Ergebnis selbst bei einfachen klassischen Problemen erheblich verbessern, was für die praktische Anwendung von Algorithmen sehr wichtig ist. In diesem Beitrag werde ich beispielsweise das Mountain Car-Problem mit einem Verstärkungstraining lösen und zeigen, dass es mit dem Wissen über die Organisation der Aufgabe viel schneller gelöst werden kann.
Über mich
Mein Name ist Oleg Svidchenko, jetzt studiere ich an der Fakultät für Physik, Mathematik und Informatik der HSE in St. Petersburg, bevor ich drei Jahre an der Universität in St. Petersburg studierte. Ich arbeite auch als Forscher bei JetBrains Research. Bevor ich an die Universität kam, studierte ich am SSC der Moskauer Staatlichen Universität und wurde als Teil des Moskauer Teams der Gewinner der Allrussischen Olympiade der Schüler der Informatik.
Was brauchen wir
Wenn Sie an einem Verstärkungstraining interessiert sind, ist die Mountain Car-Herausforderung genau das Richtige für Sie. Heute benötigen wir Python mit den installierten
Gym- und
PyTorch-Bibliotheken sowie Grundkenntnisse über neuronale Netze.
Aufgabenbeschreibung
In einer zweidimensionalen Welt muss ein Auto von der Mulde zwischen zwei Hügeln auf die Spitze des rechten Hügels klettern. Es wird durch die Tatsache kompliziert, dass sie nicht genug Motorleistung hat, um die Schwerkraft zu überwinden und beim ersten Versuch dort einzutreten. Wir sind eingeladen, einen Agenten (in unserem Fall ein neuronales Netzwerk) auszubilden, der durch Steuerung so schnell wie möglich den rechten Hügel erklimmen kann.
Die Maschinensteuerung erfolgt durch Interaktion mit der Umgebung. Es ist in unabhängige Episoden unterteilt und jede Episode wird Schritt für Schritt ausgeführt. Bei jedem Schritt empfängt der Agent den Status
s und die Umgebung
r von der Umgebung als Antwort auf die Aktion
a . Außerdem meldet das Medium manchmal zusätzlich, dass die Episode beendet ist. In diesem Problem ist
s ein Zahlenpaar, von dem die erste die Position des Autos auf der Kurve ist (eine Koordinate reicht aus, da wir uns nicht von der Oberfläche losreißen können), und die zweite ist die Geschwindigkeit auf der Oberfläche (mit einem Vorzeichen). Die Belohnung
r ist eine Zahl, die für diese Aufgabe immer gleich -1 ist. Auf diese Weise ermutigen wir den Agenten, die Episode so schnell wie möglich abzuschließen. Es gibt nur drei mögliche Aktionen: Schieben Sie das Auto nach links, tun Sie nichts und schieben Sie das Auto nach rechts. Diese Aktionen entsprechen Zahlen von 0 bis 2. Die Episode kann enden, wenn das Auto die Spitze des rechten Hügels erreicht oder wenn der Agent 200 Schritte unternommen hat.
Ein bisschen Theorie
Auf Habré gab es bereits einen
Artikel über DQN, in dem der Autor alle notwendigen Theorien ziemlich gut beschrieb. Um das Lesen zu erleichtern, werde ich es hier in einer formelleren Form wiederholen.
Die Verstärkungslernaufgabe wird durch einen Satz von Zustandsraum S, Aktionsraum A, Koeffizient definiert
Im Allgemeinen können die Übergangsfunktion und die Belohnungsfunktion Zufallsvariablen sein, aber jetzt betrachten wir eine einfachere Version, in der sie eindeutig definiert sind. Ziel ist es, die kumulierten Belohnungen zu maximieren.
Dabei ist t die Schrittnummer im Medium und T die Anzahl der Schritte in der Episode.
Um dieses Problem zu lösen, definieren wir die Wertfunktion V des Zustands s als den Wert der maximalen kumulativen Belohnung, vorausgesetzt, wir beginnen im Zustand s. Wenn wir eine solche Funktion kennen, können wir das Problem einfach lösen, indem wir bei jedem Schritt s mit dem maximal möglichen Wert übergeben. Es ist jedoch nicht alles so einfach: In den meisten Fällen wissen wir nicht, welche Aktion uns in den gewünschten Zustand bringt. Daher fügen wir die Aktion a als zweiten Parameter der Funktion hinzu. Die resultierende Funktion wird als Q-Funktion bezeichnet. Es zeigt, welche maximal mögliche kumulative Belohnung wir erhalten können, wenn wir die Aktion a in state s ausführen. Aber wir können diese Funktion bereits verwenden, um das Problem zu lösen: Wenn wir uns im Zustand s befinden, wählen wir einfach a so, dass Q (s, a) maximal ist.
In der Praxis kennen wir die reale Q-Funktion nicht, können sie aber mit verschiedenen Methoden approximieren. Eine solche Technik ist das Deep Q Network (DQN). Seine Idee ist, dass wir für jede der Aktionen die Q-Funktion unter Verwendung eines neuronalen Netzwerks approximieren.
Die Umwelt
Jetzt lass uns üben. Zunächst müssen wir lernen, wie die MountainCar-Umgebung emuliert wird. Die Turnhallenbibliothek, die eine große Anzahl von Standard-Lernumgebungen zur Verstärkung bietet, wird uns bei der Bewältigung dieser Aufgabe helfen. Um eine Umgebung zu erstellen, müssen wir die make-Methode im Fitness-Studio-Modul aufrufen und den Namen der gewünschten Umgebung als Parameter übergeben:
import gym env = gym.make("MountainCar-v0")
Eine ausführliche Dokumentation finden Sie
hier und eine Beschreibung der Umgebung finden Sie
hier .
Lassen Sie uns genauer betrachten, was wir mit der von uns geschaffenen Umgebung tun können:
env.reset() - beendet die aktuelle Episode und startet eine neue. Gibt den Ausgangszustand zurück.env.step(action) - führt die angegebene Aktion aus. Gibt einen neuen Status, eine Belohnung, ob die Episode beendet wurde und zusätzliche Informationen zurück, die zum Debuggen verwendet werden können.env.seed(seed) - setzt zufälligen Samen. Dies hängt davon ab, wie die Anfangszustände während env.reset () generiert werden.env.render() - env.render() den aktuellen Status der Umgebung an.
Wir realisieren DQN
DQN ist ein Algorithmus, der ein neuronales Netzwerk verwendet, um eine Q-Funktion zu bewerten. Im
ursprünglichen Artikel definierte DeepMind die Standardarchitektur für Atari-Spiele unter Verwendung von Faltungs-Neuronalen Netzen. Im Gegensatz zu diesen Spielen verwendet Mountain Car das Bild nicht als Status, daher müssen wir die Architektur selbst bestimmen.
Nehmen wir zum Beispiel eine Architektur mit zwei versteckten Schichten von jeweils 32 Neuronen. Nach jeder verborgenen Ebene verwenden wir
ReLU als Aktivierungsfunktion. Zwei Zahlen, die den Zustand beschreiben, werden dem Eingang des neuronalen Netzwerks zugeführt, und am Ausgang erhalten wir eine Schätzung der Q-Funktion.
import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model)
Da wir das neuronale Netzwerk auf der GPU trainieren werden, müssen wir unser Netzwerk dort laden:
Die Gerätevariable ist global, da wir auch die Daten laden müssen.
Wir müssen auch einen Optimierer definieren, der die Modellgewichte mithilfe des Gradientenabfalls aktualisiert. Ja, es gibt viel mehr als eine.
optimizer = optim.Adam(model.parameters(), lr=0.00003)
Alle zusammen import torch.nn as nn import torch device = torch.device("cuda") def create_new_model(): model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model)
Deklarieren Sie nun eine Funktion, die die Fehlerfunktion und den Gradienten entlang berücksichtigt, und wenden Sie den Abstieg an. Zuvor müssen Sie jedoch Daten aus dem Stapel auf die GPU herunterladen:
state, action, reward, next_state, done = batch
Als nächstes müssen wir die realen Werte der Q-Funktion berechnen. Da wir sie jedoch nicht kennen, werden wir sie anhand der Werte für den folgenden Zustand bewerten:
target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad():
Und die aktuelle Vorhersage:
q = model(state).gather(1, action.unsqueeze(1))
Mit target_q und q berechnen wir die Verlustfunktion und aktualisieren das Modell:
loss = F.smooth_l1_loss(q, target_q.unsqueeze(1))
Alle zusammen gamma = 0.99 def fit(batch, model, target_model, optimizer): state, action, reward, next_state, done = batch
Da das Modell nur die Q-Funktion berücksichtigt und keine Aktionen ausführt, müssen wir die Funktion bestimmen, die entscheidet, welche Aktionen der Agent ausführen wird. Als Entscheidungsalgorithmus nehmen wir
-grüne Politik. Ihre Idee ist, dass der Agent normalerweise gierig Aktionen ausführt und das Maximum der Q-Funktion wählt, aber mit Wahrscheinlichkeit
Er wird eine zufällige Aktion ausführen. Es sind zufällige Aktionen erforderlich, damit der Algorithmus die Aktionen untersuchen kann, die er nicht ausgeführt hätte, wenn er nur von einer gierigen Richtlinie geleitet würde. Dieser Prozess wird als Exploration bezeichnet.
def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item()
Da wir Stapel verwenden, um das neuronale Netzwerk zu trainieren, benötigen wir einen Puffer, in dem wir die Erfahrung der Interaktion mit der Umgebung speichern und aus dem wir Stapel auswählen:
class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """ """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """ """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory)
Naive Entscheidung
Deklarieren Sie zunächst die Konstanten, die wir im Lernprozess verwenden werden, und erstellen Sie ein Modell:
Trotz der Tatsache, dass es logisch wäre, den Interaktionsprozess in Episoden zu unterteilen, ist es für uns bequemer, den Lernprozess in separate Schritte zu unterteilen, da wir nach jedem Schritt der Umgebung einen Schritt des Gradientenabfalls machen möchten.
Lassen Sie uns genauer darüber sprechen, wie ein Lernschritt hier aussieht. Wir gehen davon aus, dass wir jetzt einen Schritt mit der Schrittanzahl der max_steps-Schritte und dem aktuellen Status machen. Dann mache die Aktion mit
-grüne Richtlinien würden so aussehen:
epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action)
Fügen Sie die gesammelten Erfahrungen sofort in das Gedächtnis ein und starten Sie eine neue Episode, wenn die aktuelle beendet ist:
memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state
Und wir werden den Schritt des Gradientenabstiegs machen (wenn wir natürlich bereits mindestens eine Charge sammeln können):
if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer)
Jetzt muss noch target_model aktualisiert werden:
if step % target_update == 0: target_model = copy.deepcopy(model)
Wir möchten aber auch den Lernprozess verfolgen. Zu diesem Zweck spielen wir nach jedem Update von target_model mit epsilon = 0 eine zusätzliche Episode ab, in der die Gesamtprämie im Puffer belohnt_by_target_updates gespeichert wird:
if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward)
Führen Sie diesen Code aus und erhalten Sie so etwas wie dieses Diagramm:
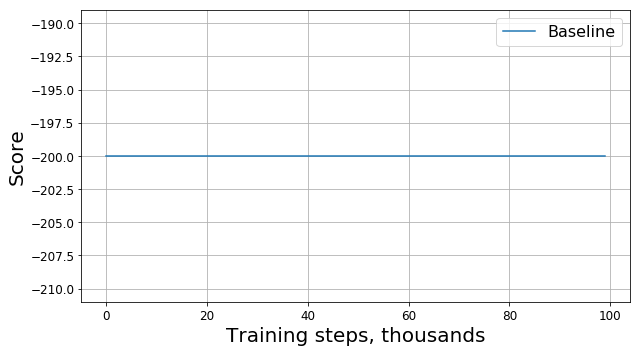
Was ist schief gelaufen?
Ist das ein Fehler? Ist das der falsche Algorithmus? Sind das schlechte Parameter? Nicht wirklich. Tatsächlich liegt das Problem in der Aufgabe, nämlich in der Funktion der Belohnung. Schauen wir es uns genauer an. Bei jedem Schritt erhält unser Agent eine Belohnung von -1, und dies geschieht bis zum Ende der Episode. Eine solche Belohnung motiviert den Agenten, die Episode so schnell wie möglich zu beenden, sagt ihm aber gleichzeitig nicht, wie es geht. Aus diesem Grund besteht die einzige Möglichkeit zu lernen, wie ein Problem in einer solchen Formulierung für einen Agenten gelöst werden kann, darin, es viele Male mithilfe von Exploration zu lösen.
Natürlich könnte man versuchen, komplexere Algorithmen zu verwenden, um die Umgebung zu untersuchen, anstatt unsere
-grüne Richtlinien. Zum einen wird unser Modell jedoch aufgrund ihrer Anwendung komplexer, was wir vermeiden möchten, und zum anderen nicht, dass sie für diese Aufgabe gut genug funktionieren. Stattdessen können wir die Ursache des Problems beseitigen, indem wir die Aufgabe selbst modifizieren, nämlich indem wir die Belohnungsfunktion ändern, d. H. durch Anwenden der sogenannten Belohnungsformung.
Beschleunigung der Konvergenz
Unser intuitives Wissen sagt uns, dass Sie beschleunigen müssen, um den Berg hinaufzufahren. Je höher die Geschwindigkeit, desto näher ist der Agent an der Lösung des Problems. Sie können ihm dies beispielsweise mitteilen, indem Sie der Belohnung ein Geschwindigkeitsmodul mit einem bestimmten Koeffizienten hinzufügen:
modifizierter_Reward = Belohnung + 10 * abs (neuer_Zustand [1])
Dementsprechend passt eine Linie in die Funktion
memory.push ((Status, Aktion, Belohnung, neuer_Zustand, erledigt))
sollte ersetzt werden durch
memory.push ((Status, Aktion, modifizierter_Reward, neuer_Zustand, erledigt))
Schauen wir uns nun das neue Diagramm an (es präsentiert die
ursprüngliche Auszeichnung ohne Änderungen):
 Hier steht RS für Reward Shaping.
Hier steht RS für Reward Shaping.Ist es gut das zu tun?
Der Fortschritt ist offensichtlich: Unser Agent hat eindeutig gelernt, den Berg hinaufzufahren, da sich die Auszeichnung von -200 zu unterscheiden begann. Es bleibt nur noch eine Frage: Wenn wir die Funktion der Belohnung ändern, ändern wir auch die Aufgabe selbst. Wird die Lösung für das neue Problem, das wir gefunden haben, für das alte Problem gut sein?
Zunächst verstehen wir, was „Güte“ in unserem Fall bedeutet. Um das Problem zu lösen, versuchen wir, die optimale Richtlinie zu finden - eine, die die Gesamtbelohnung für die Episode maximiert. In diesem Fall können wir das Wort „gut“ durch das Wort „optimal“ ersetzen, weil wir danach suchen. Wir hoffen auch optimistisch, dass unser DQN früher oder später die optimale Lösung für das modifizierte Problem findet und nicht an einem lokalen Maximum hängen bleibt. Die Frage kann also wie folgt umformuliert werden: Wenn wir die Funktion der Belohnung ändern, haben wir auch das Problem selbst geändert. Ist die optimale Lösung für das neue Problem, das wir für das alte Problem als optimal befunden haben, optimal?
Wie sich herausstellt, können wir im allgemeinen Fall keine solche Garantie geben. Die Antwort hängt davon ab, wie genau wir die Funktion der Belohnung geändert haben, wie sie früher angeordnet wurde und wie die Umgebung selbst angeordnet ist. Glücklicherweise gibt es
einen Artikel, dessen Autoren untersucht haben, wie sich eine Änderung der Funktion der Belohnung auf die Optimalität der gefundenen Lösung auswirkt.
Zunächst fanden sie eine ganze Klasse von „sicheren“ Änderungen, die auf der potenziellen Methode basieren:
wo
- Potenzial, das nur vom Staat abhängt. Für solche Funktionen konnten die Autoren nachweisen, dass die optimale Lösung für das neue Problem auch für das alte Problem optimal ist.
Zweitens zeigten die Autoren das für jeden anderen
Es gibt ein solches Problem, die R-Belohnungsfunktion und die optimale Lösung für das geänderte Problem, dass diese Lösung für das ursprüngliche Problem nicht optimal ist. Dies bedeutet, dass wir die Güte der gefundenen Lösung nicht garantieren können, wenn wir eine Änderung verwenden, die nicht auf der potenziellen Methode basiert.
Daher kann die Verwendung potenzieller Funktionen zum Modifizieren der Belohnungsfunktion nur die Konvergenzrate des Algorithmus ändern, hat jedoch keinen Einfluss auf die endgültige Lösung.
Beschleunigen Sie die Konvergenz richtig
Nachdem wir nun wissen, wie die Belohnung sicher geändert werden kann, versuchen wir, die Aufgabe erneut zu ändern, indem wir die potenzielle Methode anstelle der naiven Heuristik verwenden:
modifizierter_Preis = Belohnung + 300 * (gamma * abs (neuer_Zustand [1]) - abs (Zustand [1]))
Schauen wir uns den Zeitplan der ursprünglichen Auszeichnung an:

Wie sich herausstellte, verbesserte das Ändern der Belohnung mit Hilfe potenzieller Funktionen neben theoretischen Garantien auch das Ergebnis erheblich, insbesondere in den frühen Stadien. Natürlich besteht die Möglichkeit, dass optimalere Hyperparameter (zufälliger Keim, Gamma und andere Koeffizienten) für das Training des Agenten ausgewählt werden können, aber die Belohnungsformung erhöht die Rate der Modellkonvergenz dennoch erheblich.
Nachwort
Vielen Dank für das Lesen bis zum Ende! Ich hoffe, Ihnen hat dieser kleine praxisorientierte Ausflug in das verstärkte Lernen gefallen. Es ist klar, dass Mountain Car eine „Spielzeug“ -Aufgabe ist. Wie wir jedoch feststellen konnten, kann es schwierig sein, einem Agenten beizubringen, selbst eine scheinbar einfache Aufgabe aus menschlicher Sicht zu lösen.