Big o

Hinweis Abgekürzte Übersetzung, eher in eigenen Worten nacherzählen.
UPD: Wie in den Kommentaren erwähnt, sind die Beispiele nicht perfekt. Der Autor sucht nicht nach der besten Lösung für das Problem, sein Ziel ist es, die Komplexität der Algorithmen „an den Fingern“ zu erklären.

Die Big O-Notation wird benötigt, um die Komplexität der Algorithmen zu beschreiben. Hierfür wird das Konzept der Zeit verwendet. Das Thema ist für viele beängstigend, Programmierer, die es vermeiden, über "Zeit der Ordnung N" zu sprechen, sind eine häufige Sache.

Wenn Sie in der Lage sind, den Code in Bezug auf Big O zu bewerten, werden Sie höchstwahrscheinlich als „kluger Kerl“ angesehen. Und höchstwahrscheinlich werden Sie Ihr nächstes Interview durchgehen. Die Frage, ob es möglich ist, die Komplexität eines Codeteils auf n log n gegen n ^ 2 zu reduzieren, wird Sie nicht aufhalten.

Datenstrukturen

Die Wahl der Datenstruktur hängt von der jeweiligen Aufgabe ab: von der Art der Daten und dem Algorithmus für deren Verarbeitung. Für bestimmte Arten von Algorithmen wurden verschiedene Datenstrukturen (in .NET, Java oder Elixir) erstellt.

Bei der Auswahl der einen oder anderen Struktur kopieren wir häufig einfach die allgemein akzeptierte Lösung. In den meisten Fällen reicht dies aus. Ohne die Komplexität der Algorithmen zu verstehen, können wir jedoch keine fundierte Entscheidung treffen. Das Thema Datenstrukturen kann erst nach der Komplexität der Algorithmen übergeben werden.

Hier werden nur Arrays von Zahlen verwendet (genau wie in einem Interview). JavaScript-Beispiele.

Beginnen wir mit dem einfachsten: O (1)

Nehmen Sie ein Array von 5 Zahlen:

const nums = [1,2,3,4,5]; 

Angenommen, Sie müssen das erste Element erhalten. Wir verwenden den Index dafür:

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

Wie kompliziert ist dieser Algorithmus? Wir können sagen: "Überhaupt nicht kompliziert - nehmen Sie einfach das erste Element des Arrays." Dies ist wahr, aber es ist korrekter, die Komplexität durch die Anzahl der durchgeführten Operationen zu beschreiben, um das Ergebnis zu erzielen, abhängig von der Eingabe (Eingabeoperationen).

Mit anderen Worten: Wie viele Operationen werden mit zunehmender Anzahl von Eingabeparametern zunehmen?

In unserem Beispiel gibt es 5 Eingabeparameter, da das Array 5 Elemente enthält. Um das Ergebnis zu erhalten, müssen Sie eine Operation ausführen (ein Element nach Index nehmen). Wie viele Operationen sind erforderlich, wenn die Array-Elemente 100 sind? Oder 1000? Oder 100.000? Trotzdem ist nur eine Operation erforderlich.

Das heißt: "eine Operation für alle möglichen Eingabedaten" - O (1).

O (1) kann als "Komplexität der Ordnung 1" (Ordnung 1) oder "Algorithmus läuft in konstanter / konstanter Zeit" (konstante Zeit) gelesen werden.

Sie haben bereits vermutet, dass O (1) -Algorithmen am effizientesten sind.

Iterationen und "Zeitpunkt der Bestellung n": O (n)

Lassen Sie uns nun die Summe der Elemente des Arrays ermitteln:

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

Wieder fragen wir uns: Wie viele Eingabeoperationen benötigen wir? Hier müssen Sie alle Elemente sortieren, d. H. Operation an jedem Element. Je größer das Array, desto mehr Operationen.

Verwenden der Big O-Notation: O (n) oder „Komplexität der Ordnung n (Ordnung n)“. Diese Art von Algorithmus wird auch als "linear" bezeichnet oder der Algorithmus ist "linear skaliert".

Analyse

Können wir die Summierung effizienter gestalten? Im Allgemeinen nicht. Und wenn wir wissen, dass das Array garantiert bei 1 beginnt, sortiert ist und keine Lücken aufweist? Dann können wir die Formel S = n (n + 1) / 2 anwenden (wobei n das letzte Element des Arrays ist):

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

Ein solcher Algorithmus ist viel effizienter als O (n), außerdem wird er in "konstanter / konstanter Zeit" ausgeführt, d.h. es ist O (1).

Tatsächlich gibt es mehr als eine Operation: Sie müssen die Länge des Arrays ermitteln, das letzte Element abrufen, die Multiplikation und Division durchführen. Ist das nicht O (3) oder so? In der Big O-Notation ist die tatsächliche Anzahl der Schritte nicht wichtig. Es ist wichtig, dass der Algorithmus in konstanter Zeit ausgeführt wird.

Konstantzeitalgorithmen sind immer O (1). Das gleiche gilt für lineare Algorithmen. Tatsächlich können Operationen O (n + 5) sein. In Big O lautet die Notation O (n).

Nicht die besten Lösungen: O (n ^ 2)

Schreiben wir eine Funktion, die das Array auf Duplikate überprüft. Verschachtelte Schleifenlösung:

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

Wir wissen bereits, dass die Array-Iteration O (n) ist. Wir haben eine verschachtelte Schleife für jedes Element, das wir erneut iterieren - d. H. O (n ^ 2) oder "Komplexität der Ordnung n Quadrat".

Algorithmen mit verschachtelten Schleifen über dieselbe Sammlung sind immer O (n ^ 2).

"Die Komplexität der Reihenfolge von log n": O (log n)

Im obigen Beispiel hat eine verschachtelte Schleife für sich genommen (wenn Sie nicht berücksichtigen, dass sie verschachtelt ist) die Komplexität O (n), weil Es ist eine Aufzählung von Array-Elementen. Dieser Zyklus endet, sobald das gewünschte Element gefunden ist, d.h. Tatsächlich werden nicht alle Elemente aufgezählt. Die Big O-Notation berücksichtigt jedoch immer das Worst-Case-Szenario - der gesuchte Artikel ist möglicherweise der allerletzte.

Hier wird eine verschachtelte Schleife verwendet, um nach einem bestimmten Element in einem Array zu suchen. Die Suche nach einem Element in einem Array kann unter bestimmten Bedingungen optimiert werden - besser als lineares O (n).

Lassen Sie das Array sortiert werden. Dann können wir den binären Suchalgorithmus verwenden: Teilen Sie das Array in zwei Hälften, verwerfen Sie das Unnötige, teilen Sie das verbleibende wieder in zwei Teile und so weiter, bis wir den gewünschten Wert gefunden haben. Diese Art von Algorithmus heißt Teilen und Erobern Teilen und Erobern.



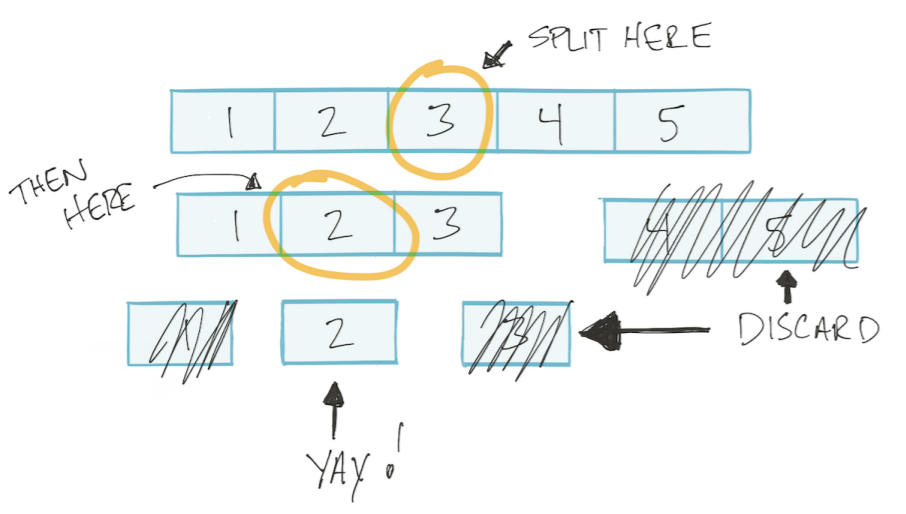
Dieser Algorithmus basiert auf einem Logarithmus.

Schneller Überblick über Logarithmen

Betrachten Sie ein Beispiel, was wird x gleich sein?

x ^ 3 = 8

Wir müssen die Kubikwurzel von 8 nehmen - dies wird 2 sein. Jetzt schwieriger

2 ^ x = 512

Mit dem Logarithmus kann das Problem wie folgt geschrieben werden

log2 (512) = x

"Der Logarithmus zur Basis 2 von 512 ist x." Achten Sie auf "Basis 2", d. H. Wir denken zu zweit - wie oft müssen Sie 2 multiplizieren, um 512 zu erhalten.

Im binären Suchalgorithmus teilen wir das Array bei jedem Schritt in zwei Teile.

Mein Zusatz. Das heißt, Im schlimmsten Fall führen wir so viele Operationen aus, wie wir das Array in zwei Teile teilen können. Wie oft können wir beispielsweise ein Array von 4 Elementen in zwei Teile aufteilen? 2 mal. Und ein Array von 8 Elementen? 3 mal. Das heißt, Anzahl der Unterteilungen / Operationen = log2 (n) (wobei n die Anzahl der Elemente im Array ist).

Es stellt sich heraus, dass die Abhängigkeit der Anzahl der Operationen von der Anzahl der Eingabeelemente als log2 (n) beschrieben wird.


Somit hat der binäre Suchalgorithmus unter Verwendung der Big O-Notation die Komplexität O (log n).

Verbessere O (n ^ 2) zu O (n log n)

Kehren wir zur Aufgabe zurück, das Array auf Duplikate zu überprüfen. Wir haben alle Elemente des Arrays durchlaufen, und für jedes Element haben wir erneut durchlaufen. Sie haben O (n) innerhalb von O (n) gemacht, d.h. O (n * n) oder O (n ^ 2).

Wir können die verschachtelte Schleife durch eine binäre Suche * ersetzen. Das heißt, wir müssen nur alle Elemente von O (n) durchgehen, im Inneren machen wir O (log n). Es stellt sich heraus, O (n * log n) oder O (n log n).

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

* ACHTUNG, um ein Aufdrucken zu vermeiden. Die Verwendung der binären Suche zum Überprüfen eines Arrays auf Duplikate ist eine schlechte Lösung. Es wird nur gezeigt, wie in Big O-Begriffen die Komplexität des in der obigen Codeliste gezeigten Algorithmus bewertet werden kann. Ein guter oder ein schlechter Algorithmus ist für diesen Artikel nicht wichtig, Sichtbarkeit ist wichtig.

Denken in Big O.

• Das Abrufen des Sammlungsgegenstandes ist O (1). Unabhängig davon, ob es sich um einen Index in einem Array oder um einen Schlüssel in einem Wörterbuch in Big O-Notation handelt, ist es O (1).
• Das Iterieren über eine Sammlung ist O (n)
• Verschachtelte Schleifen über dieselbe Sammlung sind O (n ^ 2)
• Teile und erobere immer O (log n)
• Iterationen, die Teilen und Erobern verwenden, sind O (n log n)