In den vorherigen Artikeln haben wir die PostgreSQL- Indexierungs-Engine , die Schnittstelle von Zugriffsmethoden und zwei Zugriffsmethoden erläutert: Hash-Index und B-Tree . In diesem Artikel werden GiST-Indizes beschrieben.

Kern

GiST ist eine Abkürzung für "Generalized Search Tree". Dies ist ein ausgewogener Suchbaum, genau wie der zuvor beschriebene "B-Baum".

Was ist der Unterschied? Der "Btree" -Index ist eng mit der Vergleichssemantik verbunden: Die Unterstützung von "größeren", "kleineren" und "gleichen" Operatoren ist alles, was er kann (aber sehr fähig!). Moderne Datenbanken speichern jedoch Datentypen, für die diese Operatoren geeignet sind macht einfach keinen Sinn: Geodaten, Textdokumente, Bilder, ...

Für diese Datentypen hilft uns die GiST-Indexmethode. Es ermöglicht das Definieren einer Regel zum Verteilen von Daten eines beliebigen Typs über einen ausgeglichenen Baum und eine Methode zum Verwenden dieser Darstellung für den Zugriff durch einen Operator. Beispielsweise kann der GiST-Index den R-Baum für räumliche Daten mit Unterstützung relativer Positionsoperatoren (links, rechts, enthält usw.) oder den RD-Baum für Mengen mit Unterstützung von Schnitt- oder Einschlussoperatoren "aufnehmen".

Dank der Erweiterbarkeit kann in PostgreSQL eine völlig neue Methode von Grund auf neu erstellt werden: Zu diesem Zweck muss eine Schnittstelle zur Indexierungs-Engine implementiert werden. Dies erfordert jedoch nicht nur eine vorsätzliche Indizierungslogik, sondern auch die Zuordnung von Datenstrukturen zu Seiten, die effiziente Implementierung von Sperren und die Unterstützung eines Write-Ahead-Protokolls. All dies setzt hohe Entwicklerfähigkeiten und einen großen menschlichen Aufwand voraus. GiST vereinfacht die Aufgabe, indem es Probleme auf niedriger Ebene übernimmt und eine eigene Schnittstelle bietet: verschiedene Funktionen, die sich nicht auf Techniken, sondern auf die Anwendungsdomäne beziehen. In diesem Sinne können wir GiST als Rahmen für die Erstellung neuer Zugriffsmethoden betrachten.

Struktur

GiST ist ein Baum mit ausgeglichener Höhe, der aus Knotenseiten besteht. Die Knoten bestehen aus Indexzeilen.

Jede Zeile eines Blattknotens (Blattzeile) enthält im Allgemeinen ein Prädikat (Boolescher Ausdruck) und einen Verweis auf eine Tabellenzeile (TID). Indizierte Daten (Schlüssel) müssen dieses Prädikat erfüllen.

Jede Zeile eines internen Knotens (interne Zeile) enthält auch ein Prädikat und einen Verweis auf einen untergeordneten Knoten, und alle indizierten Daten des untergeordneten Teilbaums müssen diesem Prädikat entsprechen. Mit anderen Worten, das Prädikat einer internen Zeile enthält die Prädikate aller untergeordneten Zeilen. Dieses wichtige Merkmal des GiST-Index ersetzt die einfache Reihenfolge des B-Baums.

Die Suche im GiST-Baum verwendet eine spezielle Konsistenzfunktion ("konsistent") - eine der Funktionen, die von der Schnittstelle definiert und für jede unterstützte Operatorfamilie auf ihre eigene Weise implementiert werden.

Die Konsistenzfunktion wird für eine Indexzeile aufgerufen und bestimmt, ob das Prädikat dieser Zeile mit dem Suchprädikat übereinstimmt (angegeben als " Operatorausdruck für indizierte Felder "). Für eine interne Zeile bestimmt diese Funktion tatsächlich, ob ein Abstieg zum entsprechenden Teilbaum erforderlich ist, und für eine Blattzeile bestimmt die Funktion, ob die indizierten Daten dem Prädikat entsprechen.

Die Suche beginnt mit einem Wurzelknoten wie eine normale Baumsuche. Mit der Konsistenzfunktion können Sie herausfinden, welche untergeordneten Knoten sinnvoll sind (möglicherweise mehrere) und welche nicht. Der Algorithmus wird dann für jeden gefundenen untergeordneten Knoten wiederholt. Wenn der Knoten Blatt ist, wird die von der Konsistenzfunktion ausgewählte Zeile als eines der Ergebnisse zurückgegeben.

Die Suche erfolgt in der Tiefe zuerst: Der Algorithmus versucht zunächst, einen Blattknoten zu erreichen. Dies ermöglicht es, möglichst bald erste Ergebnisse zurückzugeben (was wichtig sein kann, wenn der Benutzer nur an mehreren Ergebnissen und nicht an allen interessiert ist).

Beachten wir noch einmal, dass die Konsistenzfunktion nichts mit "größeren", "kleineren" oder "gleichen" Operatoren zu tun haben muss. Die Semantik der Konsistenzfunktion kann sehr unterschiedlich sein, und daher wird nicht angenommen, dass der Index Werte in einer bestimmten Reihenfolge zurückgibt.

Wir werden keine Algorithmen zum Einfügen und Löschen von Werten in GiST diskutieren: Einige weitere Schnittstellenfunktionen führen diese Operationen aus. Es gibt jedoch einen wichtigen Punkt. Wenn ein neuer Wert in den Index eingefügt wird, wird die Position für diesen Wert im Baum so ausgewählt, dass die Prädikate der übergeordneten Zeilen so wenig wie möglich erweitert werden (idealerweise überhaupt nicht erweitert). Wenn jedoch ein Wert gelöscht wird, wird das Prädikat der übergeordneten Zeile nicht mehr reduziert. Dies geschieht nur in solchen Fällen: Eine Seite wird in zwei Teile geteilt (wenn auf der Seite nicht genügend Platz zum Einfügen einer neuen Indexzeile vorhanden ist) oder der Index wird von Grund auf neu erstellt (mit dem Befehl REINDEX oder VACUUM FULL). Daher kann sich die Effizienz des GiST-Index für häufig wechselnde Daten im Laufe der Zeit verschlechtern.

Weiter werden wir einige Beispiele für Indizes für verschiedene Datentypen und nützliche Eigenschaften von GiST betrachten:

• Punkte (und andere geometrische Objekte) und Suche nach nächsten Nachbarn.
• Intervalle und Ausschlussbeschränkungen.
• Volltextsuche.

R-Baum für Punkte

Wir werden das Obige anhand eines Index für Punkte in einer Ebene veranschaulichen (wir können ähnliche Indizes auch für andere geometrische Objekte erstellen). Ein regulärer B-Baum passt nicht zu diesem Datentyp, da für Punkte keine Vergleichsoperatoren definiert sind.

Die Idee des R-Baums besteht darin, die Ebene in Rechtecke aufzuteilen, die insgesamt alle indizierten Punkte abdecken. In einer Indexzeile wird ein Rechteck gespeichert, und das Prädikat kann folgendermaßen definiert werden: "Der gesuchte Punkt liegt innerhalb des angegebenen Rechtecks."

Die Wurzel des R-Baums enthält mehrere größte Rechtecke (die sich möglicherweise schneiden). Untergeordnete Knoten enthalten kleinere Rechtecke, die in das übergeordnete eingebettet sind und insgesamt alle zugrunde liegenden Punkte abdecken.

Theoretisch müssen Blattknoten Punkte enthalten, die indiziert werden, aber der Datentyp muss in allen Indexzeilen gleich sein, und daher werden wieder Rechtecke gespeichert, aber zu Punkten „reduziert“.

Um eine solche Struktur zu visualisieren, stellen wir Bilder für drei Ebenen des R-Baums bereit. Punkte sind Koordinaten von Flughäfen (ähnlich wie in der Tabelle "Flughäfen" der Demo-Datenbank , es werden jedoch weitere Daten von openflights.org bereitgestellt).


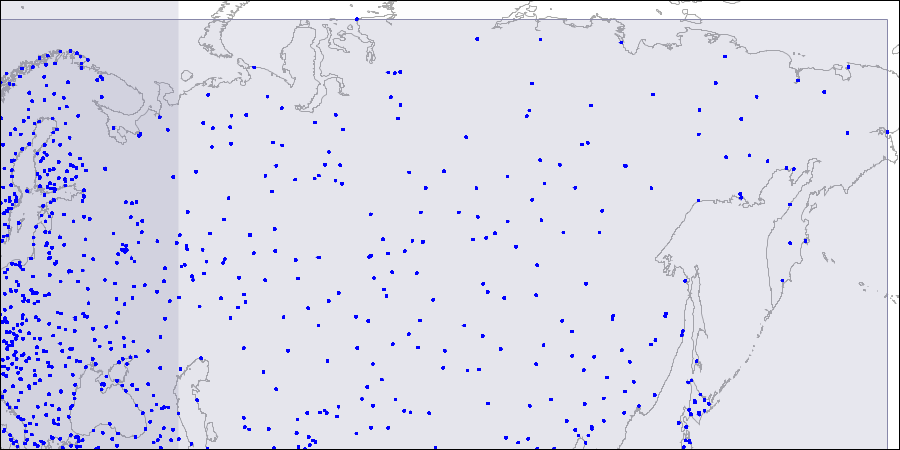Stufe eins: Zwei große sich überschneidende Rechtecke sind sichtbar.


Stufe zwei: Große Rechtecke werden in kleinere Bereiche aufgeteilt.


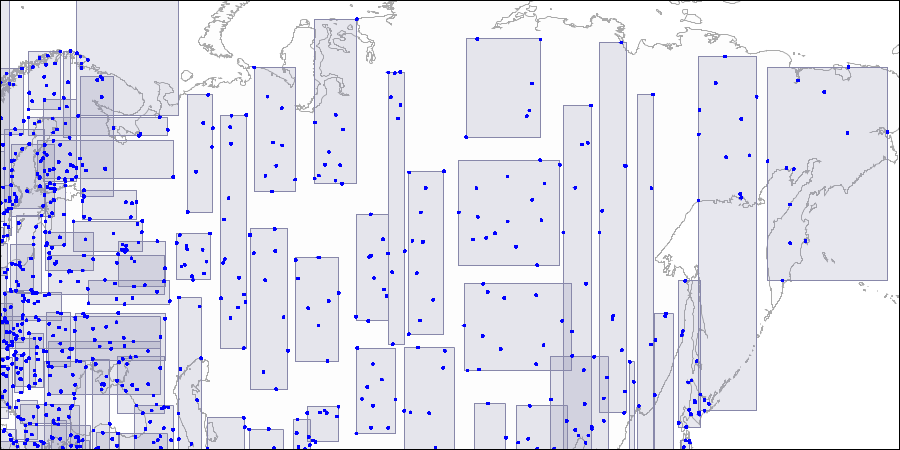Stufe drei: Jedes Rechteck enthält so viele Punkte, wie auf eine Indexseite passen.

Betrachten wir nun ein sehr einfaches "einstufiges" Beispiel:

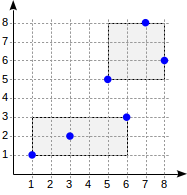
postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index on points using gist(p); 

Bei dieser Aufteilung sieht die Indexstruktur wie folgt aus:



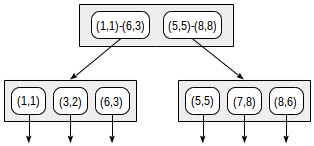
Der erstellte Index kann verwendet werden, um die folgende Abfrage zu beschleunigen, z. B. "Alle im angegebenen Rechteck enthaltenen Punkte finden". Diese Bedingung kann wie folgt formalisiert werden: p <@ box '(2,1),(6,3)' (Operator <@ aus der Familie "points_ops" bedeutet "enthalten in"):

 postgres=# set enable_seqscan = off; postgres=# explain(costs off) select * from points where p <@ box '(2,1),(7,4)'; 

  QUERY PLAN ---------------------------------------------- Index Only Scan using points_p_idx on points Index Cond: (p <@ '(7,4),(2,1)'::box) (2 rows) 

Die Konsistenzfunktion des Operators (" indiziertes Feld <@ Ausdruck ", wobei indiziertes Feld ein Punkt und Ausdruck ein Rechteck ist) ist wie folgt definiert. Für eine interne Zeile wird "Ja" zurückgegeben, wenn sich das Rechteck mit dem durch den Ausdruck definierten Rechteck schneidet. Für eine Blattzeile gibt die Funktion "Ja" zurück, wenn ihr Punkt ("reduziertes" Rechteck) in dem durch den Ausdruck definierten Rechteck enthalten ist.



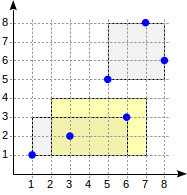
Die Suche beginnt mit dem Wurzelknoten. Das Rechteck (2,1) - (7,4) schneidet sich mit (1,1) - (6,3), schneidet sich jedoch nicht mit (5,5) - (8,8), daher besteht keine Notwendigkeit zum zweiten Teilbaum absteigen.



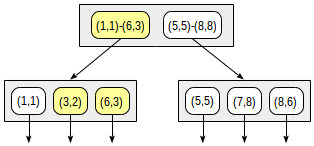
Bei Erreichen eines Blattknotens gehen wir die drei dort enthaltenen Punkte durch und geben zwei davon als Ergebnis zurück: (3.2) und (6.3).

 postgres=# select * from points where p <@ box '(2,1),(7,4)'; 

  p ------- (3,2) (6,3) (2 rows) 

Interna

Leider erlaubt die übliche "Seiteninspektion" keinen Blick in den GiST-Index. Es gibt aber auch einen anderen Weg: die Erweiterung "Gevel". Es ist nicht in der Standardlieferung enthalten, siehe Installationsanweisungen .

Wenn alles richtig gemacht ist, stehen Ihnen drei Funktionen zur Verfügung. Erstens können wir einige Statistiken erhalten:

 postgres=# select * from gist_stat('airports_coordinates_idx'); 

  gist_stat ------------------------------------------ Number of levels: 4 + Number of pages: 690 + Number of leaf pages: 625 + Number of tuples: 7873 + Number of invalid tuples: 0 + Number of leaf tuples: 7184 + Total size of tuples: 354692 bytes + Total size of leaf tuples: 323596 bytes + Total size of index: 5652480 bytes+ (1 row) 

Es ist klar, dass der Index für Flughafenkoordinaten 690 Seiten groß ist und dass der Index aus vier Ebenen besteht: Die Wurzel- und zwei interne Ebenen wurden in den obigen Abbildungen gezeigt, und die vierte Ebene ist Blatt.

Tatsächlich wird der Index für achttausend Punkte deutlich kleiner sein: Hier wurde er aus Gründen der Übersichtlichkeit mit einem 10% -Füllfaktor erstellt.

Zweitens können wir den Indexbaum ausgeben:

 postgres=# select * from gist_tree('airports_coordinates_idx'); 

  gist_tree ----------------------------------------------------------------------------------------- 0(l:0) blk: 0 numTuple: 5 free: 7928b(2.84%) rightlink:4294967295 (InvalidBlockNumber) + 1(l:1) blk: 335 numTuple: 15 free: 7488b(8.24%) rightlink:220 (OK) + 1(l:2) blk: 128 numTuple: 9 free: 7752b(5.00%) rightlink:49 (OK) + 1(l:3) blk: 57 numTuple: 12 free: 7620b(6.62%) rightlink:35 (OK) + 2(l:3) blk: 62 numTuple: 9 free: 7752b(5.00%) rightlink:57 (OK) + 3(l:3) blk: 72 numTuple: 7 free: 7840b(3.92%) rightlink:23 (OK) + 4(l:3) blk: 115 numTuple: 17 free: 7400b(9.31%) rightlink:33 (OK) + ... 

Und drittens können wir die in Indexzeilen gespeicherten Daten ausgeben. Beachten Sie die folgende Nuance: Das Ergebnis der Funktion muss in den gewünschten Datentyp umgewandelt werden. In unserer Situation ist dieser Typ "Box" (ein Begrenzungsrechteck). Beachten Sie beispielsweise fünf Zeilen auf der obersten Ebene:

 postgres=# select level, a from gist_print('airports_coordinates_idx') as t(level int, valid bool, a box) where level = 1; 

  level | a -------+----------------------------------------------------------------------- 1 | (47.663586,80.803207),(-39.2938003540039,-90) 1 | (179.951004028,15.6700000762939),(15.2428998947144,-77.9634017944336) 1 | (177.740997314453,73.5178070068359),(15.0664,10.57970047) 1 | (-77.3191986083984,79.9946975708),(-179.876998901,-43.810001373291) 1 | (-39.864200592041,82.5177993774),(-81.254096984863,-64.2382965088) (5 rows) 

Tatsächlich wurden die oben angegebenen Zahlen nur aus diesen Daten erstellt.

Operatoren für die Suche und Bestellung

Bisher diskutierte Operatoren (wie <@ im Prädikat p <@ box '(2,1),(7,4)' ) können als Suchoperatoren bezeichnet werden, da sie Suchbedingungen in einer Abfrage angeben.

Es gibt auch einen anderen Operatortyp: Bestelloperatoren. Sie werden für Spezifikationen der Sortierreihenfolge in der ORDER BY-Klausel anstelle herkömmlicher Spezifikationen für Spaltennamen verwendet. Das Folgende ist ein Beispiel für eine solche Abfrage:

 postgres=# select * from points order by p <-> point '(4,7)' limit 2; 

  p ------- (5,5) (7,8) (2 rows) 

p <-> point '(4,7)' hier ein Ausdruck, der einen Ordnungsoperator <-> , der den Abstand von einem Argument zum anderen angibt. Die Bedeutung der Abfrage besteht darin, zwei Punkte zurückzugeben, die dem Punkt am nächsten liegen (4.7). Eine solche Suche wird als k-NN - k-Suche nach dem nächsten Nachbarn bezeichnet.

Um Abfragen dieser Art zu unterstützen, muss eine Zugriffsmethode eine zusätzliche Distanzfunktion definieren, und der Bestelloperator muss in der entsprechenden Operatorklasse enthalten sein (z. B. "points_ops" -Klasse für Punkte). Die folgende Abfrage zeigt Operatoren mit ihren Typen ("s" - Suche und "o" - Reihenfolge):

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------+-------------+-------------- <<(point,point) | s | 1 strictly left >>(point,point) | s | 5 strictly right ~=(point,point) | s | 6 coincides <^(point,point) | s | 10 strictly below >^(point,point) | s | 11 strictly above <->(point,point) | o | 15 distance <@(point,box) | s | 28 contained in rectangle <@(point,polygon) | s | 48 contained in polygon <@(point,circle) | s | 68 contained in circle (9 rows) 

Die Anzahl der Strategien wird ebenfalls angezeigt und ihre Bedeutung erklärt. Es ist klar, dass es weit mehr Strategien als für "btree" gibt, von denen nur einige für Punkte unterstützt werden. Für andere Datentypen können unterschiedliche Strategien definiert werden.

Die Distanzfunktion wird für ein Indexelement aufgerufen und muss die Distanz (unter Berücksichtigung der Operatorsemantik) von dem durch den Ausdruck definierten Wert (" indizierter Feldordnungsoperatorausdruck ") zu dem angegebenen Element berechnen. Bei einem Blattelement ist dies nur der Abstand zum indizierten Wert. Für ein internes Element muss die Funktion das Minimum der Abstände zu den untergeordneten Blattelementen zurückgeben. Da das Durchsuchen aller untergeordneten Zeilen ziemlich kostspielig wäre, kann die Funktion die Entfernung optimistisch unterschätzen, jedoch auf Kosten der Verringerung der Sucheffizienz. Die Funktion darf jedoch niemals die Entfernung überschätzen, da dies die Arbeit des Index stört.

Die Distanzfunktion kann Werte eines beliebigen sortierbaren Typs zurückgeben (um Werte zu ordnen, verwendet PostgreSQL die Vergleichssemantik aus der entsprechenden Operatorfamilie der Zugriffsmethode "btree", wie zuvor beschrieben ).

Für Punkte in einer Ebene wird der Abstand in einem sehr üblichen Sinne interpretiert: Der Wert von (x1,y1) <-> (x2,y2) entspricht der Quadratwurzel der Summe der Quadrate der Differenzen der Abszissen und Ordinaten. Der Abstand von einem Punkt zu einem Begrenzungsrechteck wird als minimaler Abstand vom Punkt zu diesem Rechteck oder als Null angenommen, wenn der Punkt innerhalb des Rechtecks ​​liegt. Es ist einfach, diesen Wert zu berechnen, ohne durch untergeordnete Punkte zu gehen, und der Wert ist mit Sicherheit nicht größer als der Abstand zu einem untergeordneten Punkt.

Betrachten wir den Suchalgorithmus für die obige Abfrage.



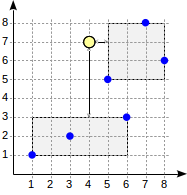
Die Suche beginnt mit dem Wurzelknoten. Der Knoten enthält zwei Begrenzungsrechtecke. Der Abstand zu (1,1) - (6,3) beträgt 4,0 und zu (5,5) - (8,8) beträgt 1,0.

Untergeordnete Knoten werden in der Reihenfolge der Vergrößerung durchlaufen. Auf diese Weise steigen wir zuerst zum nächsten untergeordneten Knoten ab und berechnen die Abstände zu den Punkten (wir zeigen die Zahlen in der Abbildung zur besseren Sichtbarkeit):



Diese Information reicht aus, um die ersten beiden Punkte (5,5) und (7,8) zurückzugeben. Da wir uns bewusst sind, dass der Abstand zu Punkten, die innerhalb des Rechtecks ​​(1,1) - (6,3) liegen, 4,0 oder mehr beträgt, müssen wir nicht zum ersten untergeordneten Knoten absteigen.

Aber was wäre, wenn wir die ersten drei Punkte finden müssten?

 postgres=# select * from points order by p <-> point '(4,7)' limit 3; 

  p ------- (5,5) (7,8) (8,6) (3 rows) 

Obwohl der zweite untergeordnete Knoten alle diese Punkte enthält, können wir nicht zurückkehren (8,6), ohne in den ersten untergeordneten Knoten zu schauen, da dieser Knoten nähere Punkte enthalten kann (da 4.0 <4.1).



In diesem Beispiel werden für interne Zeilen die Anforderungen für die Abstandsfunktion erläutert. Durch Auswahl eines kleineren Abstands (4,0 anstelle des tatsächlichen Abstands 4,5) für die zweite Zeile haben wir die Effizienz verringert (der Algorithmus hat unnötigerweise begonnen, einen zusätzlichen Knoten zu untersuchen), aber die Korrektheit des Algorithmus nicht beeinträchtigt.

Bis vor kurzem war GiST die einzige Zugriffsmethode, die mit bestellenden Betreibern umgehen konnte. Die Situation hat sich jedoch geändert: Die RUM-Zugriffsmethode (wird weiter diskutiert) hat sich bereits dieser Gruppe von Methoden angeschlossen, und es ist nicht unwahrscheinlich, dass sich ein guter alter B-Baum ihnen anschließt: Ein Patch, der von Nikita Glukhov, unserem Kollegen, entwickelt wurde, wird gerade erstellt von der Community diskutiert.

Ab März 2019 wird k-NN-Unterstützung für SP-GiST im kommenden PostgreSQL 12 (ebenfalls von Nikita verfasst) hinzugefügt. Patch für B-Tree ist noch in Bearbeitung.

R-Baum für Intervalle

Ein weiteres Beispiel für die Verwendung der GiST-Zugriffsmethode ist die Indizierung von Intervallen, z. B. Zeitintervallen (Typ "tsrange"). Der Unterschied besteht darin, dass interne Knoten Begrenzungsintervalle anstelle von Begrenzungsrechtecken enthalten.

Betrachten wir ein einfaches Beispiel. Wir werden ein Ferienhaus vermieten und Reservierungsintervalle in einer Tabelle speichern:

 postgres=# create table reservations(during tsrange); postgres=# insert into reservations(during) values ('[2016-12-30, 2017-01-09)'), ('[2017-02-23, 2017-02-27)'), ('[2017-04-29, 2017-05-02)'); postgres=# create index on reservations using gist(during); 

Der Index kann verwendet werden, um beispielsweise die folgende Abfrage zu beschleunigen:

 postgres=# select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  during ----------------------------------------------- ["2016-12-30 00:00:00","2017-01-08 00:00:00") ["2017-02-23 00:00:00","2017-02-26 00:00:00") (2 rows) 

 postgres=# explain (costs off) select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  QUERY PLAN ------------------------------------------------------------------------------------ Index Only Scan using reservations_during_idx on reservations Index Cond: (during && '["2017-01-01 00:00:00","2017-04-01 00:00:00")'::tsrange) (2 rows) 

&& Operator für Intervalle bezeichnet Schnittpunkt; Daher muss die Abfrage alle Intervalle zurückgeben, die sich mit dem angegebenen Intervall überschneiden. Für einen solchen Operator bestimmt die Konsistenzfunktion, ob sich das angegebene Intervall mit einem Wert in einer internen oder einer Blattzeile überschneidet.

Beachten Sie, dass es entweder nicht darum geht, Intervalle in einer bestimmten Reihenfolge abzurufen, obwohl Vergleichsoperatoren für Intervalle definiert sind. Wir können den "btree" -Index für Intervalle verwenden, aber in diesem Fall müssen wir auf die Unterstützung solcher Operationen verzichten:

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'range_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------------+-------------+-------------- @>(anyrange,anyelement) | s | 16 contains element <<(anyrange,anyrange) | s | 1 strictly left &<(anyrange,anyrange) | s | 2 not beyond right boundary &&(anyrange,anyrange) | s | 3 intersects &>(anyrange,anyrange) | s | 4 not beyond left boundary >>(anyrange,anyrange) | s | 5 strictly right -|-(anyrange,anyrange) | s | 6 adjacent @>(anyrange,anyrange) | s | 7 contains interval <@(anyrange,anyrange) | s | 8 contained in interval =(anyrange,anyrange) | s | 18 equals (10 rows) 

(Mit Ausnahme der Gleichheit, die in der Operatorklasse für die Zugriffsmethode "btree" enthalten ist.)

Interna

Wir können mit der gleichen "Gevel" -Erweiterung nach innen schauen. Wir müssen nur daran denken, den Datentyp im Aufruf von gist_print zu ändern:

 postgres=# select level, a from gist_print('reservations_during_idx') as t(level int, valid bool, a tsrange); 

  level | a -------+----------------------------------------------- 1 | ["2016-12-30 00:00:00","2017-01-09 00:00:00") 1 | ["2017-02-23 00:00:00","2017-02-27 00:00:00") 1 | ["2017-04-29 00:00:00","2017-05-02 00:00:00") (3 rows) 

Ausschlussbeschränkung

Der GiST-Index kann zur Unterstützung von Ausschlussbeschränkungen (EXCLUDE) verwendet werden.

Die Ausschlussbeschränkung stellt sicher, dass bestimmte Felder von zwei beliebigen Tabellenzeilen in Bezug auf einige Operatoren nicht miteinander "korrespondieren". Wenn der Operator "gleich" gewählt wird, erhalten wir genau die eindeutige Einschränkung: Die angegebenen Felder von zwei beliebigen Zeilen sind nicht gleich.

Die Ausschlussbeschränkung wird vom Index sowie von der eindeutigen Einschränkung unterstützt. Wir können jeden Operator so auswählen, dass:

1. Es wird von der Indexmethode "can_exclude" unterstützt (z. B. "btree", GiST oder SP-GiST, jedoch nicht GIN).
2. Es ist kommutativ, dh die Bedingung ist erfüllt: a Operator b = b Operator a.

Dies ist eine Liste geeigneter Strategien und Beispiele für Operatoren (Operatoren können, wie wir uns erinnern, unterschiedliche Namen haben und nicht für alle Datentypen verfügbar sein):

• Für "btree":
  
  • "Gleich" =
• Für GiST und SP-GiST:
  
  • "Kreuzung" &&
  • "Zufall" ~=
  • Nachbarschaft -|-

Beachten Sie, dass wir den Gleichheitsoperator in einer Ausschlussbedingung verwenden können, dies jedoch unpraktisch ist: Eine eindeutige Einschränkung ist effizienter. Genau deshalb haben wir bei der Erörterung von B-Bäumen keine Ausschlussbeschränkungen angesprochen.

Lassen Sie uns ein Beispiel für die Verwendung einer Ausschlussbeschränkung geben. Es ist vernünftig, keine Reservierungen für sich überschneidende Intervalle zuzulassen.

 postgres=# alter table reservations add exclude using gist(during with &&); 

Sobald wir die Ausschlussbeschränkung erstellt haben, können wir Zeilen hinzufügen:

 postgres=# insert into reservations(during) values ('[2017-06-10, 2017-06-13)'); 

Der Versuch, ein Schnittintervall in die Tabelle einzufügen, führt jedoch zu einem Fehler:

 postgres=# insert into reservations(during) values ('[2017-05-15, 2017-06-15)'); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_excl" DETAIL: Key (during)=(["2017-05-15 00:00:00","2017-06-15 00:00:00")) conflicts with existing key (during)=(["2017-06-10 00:00:00","2017-06-13 00:00:00")). 

Erweiterung "Btree_gist"

Lassen Sie uns das Problem komplizieren. Wir erweitern unser bescheidenes Geschäft und werden mehrere Cottages vermieten:

 postgres=# alter table reservations add house_no integer default 1; 

Wir müssen die Ausschlussbeschränkung ändern, damit die Hausnummern berücksichtigt werden. GiST unterstützt jedoch nicht die Gleichheitsoperation für Ganzzahlen:

 postgres=# alter table reservations drop constraint reservations_during_excl; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

 ERROR: data type integer has no default operator class for access method "gist" HINT: You must specify an operator class for the index or define a default operator class for the data type. 

In diesem Fall hilft die Erweiterung " btree_gist ", die die GiST-Unterstützung für Operationen hinzufügt, die B-Bäumen eigen sind. GiST kann schließlich alle Operatoren unterstützen. Warum sollten wir es nicht lehren, "größere", "kleinere" und "gleiche" Operatoren zu unterstützen?

 postgres=# create extension btree_gist; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

Jetzt können wir das erste Cottage noch nicht für die gleichen Daten reservieren:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 1); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_house_no_excl" 

Wir können jedoch den zweiten reservieren:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 2); 

Beachten Sie jedoch, dass GiST die Operatoren "größer", "kleiner" und "gleich" zwar irgendwie unterstützen kann, B-tree dies jedoch immer noch besser kann. Daher lohnt es sich, diese Technik nur zu verwenden, wenn der GiST-Index im Wesentlichen benötigt wird, wie in unserem Beispiel.

RD-Baum für die Volltextsuche

Über die Volltextsuche

Beginnen wir mit einer minimalistischen Einführung in die PostgreSQL-Volltextsuche (wenn Sie sich auskennen, können Sie diesen Abschnitt überspringen).

Die Aufgabe der Volltextsuche besteht darin, aus dem Dokumentensatz diejenigen Dokumente auszuwählen, die der Suchabfrage entsprechen. (Wenn es viele übereinstimmende Dokumente gibt, ist es wichtig, die besten übereinstimmenden Dokumente zu finden, aber wir werden an dieser Stelle nichts dazu sagen.)

Zu Suchzwecken wird ein Dokument in einen speziellen Typ "tsvector" konvertiert, der Lexeme und ihre Positionen im Dokument enthält. Lexeme sind Wörter, die in die für die Suche geeignete Form konvertiert wurden. Beispielsweise werden Wörter normalerweise in Kleinbuchstaben umgewandelt und variable Endungen abgeschnitten:

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile'); 

  to_tsvector ----------------------------------------- 'crook':4,10 'man':5 'mile':11 'walk':8 (1 row) 

Wir können auch sehen, dass einige Wörter ( Stoppwörter genannt ) vollständig gelöscht werden ("dort", "war", "a", "und", er "), da sie vermutlich zu oft vorkommen, als dass eine Suche nach ihnen sinnvoll wäre. All diese Konvertierungen können sicherlich konfiguriert werden, aber das ist eine andere Geschichte.

Eine Suchabfrage wird mit einem anderen Typ dargestellt: "tsquery". Eine Abfrage besteht ungefähr aus einem oder mehreren Lexemen, die durch Konnektive verbunden sind: "und" & "oder" |, "nicht"! .. Wir können auch Klammern verwenden, um die Priorität der Operation zu klären.

 postgres=# select to_tsquery('man & (walking | running)'); 

  to_tsquery ---------------------------- 'man' & ( 'walk' | 'run' ) (1 row) 

Für die @@ wird nur ein Übereinstimmungsoperator @@ verwendet.

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (walking | running)'); 

  ?column? ---------- t (1 row) 

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (going | running)'); 

  ?column? ---------- f (1 row) 

Diese Information reicht vorerst aus. In einem nächsten Artikel mit GIN-Index werden wir uns etwas eingehender mit der Volltextsuche befassen.

RD-Bäume

Für eine schnelle Volltextsuche muss zum einen in der Tabelle eine Spalte vom Typ "tsvector" gespeichert werden (um zu vermeiden, dass bei der Suche jedes Mal eine kostspielige Konvertierung durchgeführt wird), und zum anderen muss ein Index für diese Spalte erstellt werden. Eine der möglichen Zugriffsmethoden hierfür ist GiST.

 postgres=# create table ts(doc text, doc_tsv tsvector); postgres=# create index on ts using gist(doc_tsv); postgres=# insert into ts(doc) values ('Can a sheet slitter slit sheets?'), ('How many sheets could a sheet slitter slit?'), ('I slit a sheet, a sheet I slit.'), ('Upon a slitted sheet I sit.'), ('Whoever slit the sheets is a good sheet slitter.'), ('I am a sheet slitter.'), ('I slit sheets.'), ('I am the sleekest sheet slitter that ever slit sheets.'), ('She slits the sheet she sits on.'); postgres=# update ts set doc_tsv = to_tsvector(doc); 

Es ist sicherlich zweckmäßig, einen Auslöser mit dem letzten Schritt zu beauftragen (Konvertierung des Dokuments in "tsvector").

 postgres=# select * from ts; 

 -[ RECORD 1 ]---------------------------------------------------- doc | Can a sheet slitter slit sheets? doc_tsv | 'sheet':3,6 'slit':5 'slitter':4 -[ RECORD 2 ]---------------------------------------------------- doc | How many sheets could a sheet slitter slit? doc_tsv | 'could':4 'mani':2 'sheet':3,6 'slit':8 'slitter':7 -[ RECORD 3 ]---------------------------------------------------- doc | I slit a sheet, a sheet I slit. doc_tsv | 'sheet':4,6 'slit':2,8 -[ RECORD 4 ]---------------------------------------------------- doc | Upon a slitted sheet I sit. doc_tsv | 'sheet':4 'sit':6 'slit':3 'upon':1 -[ RECORD 5 ]---------------------------------------------------- doc | Whoever slit the sheets is a good sheet slitter. doc_tsv | 'good':7 'sheet':4,8 'slit':2 'slitter':9 'whoever':1 -[ RECORD 6 ]---------------------------------------------------- doc | I am a sheet slitter. doc_tsv | 'sheet':4 'slitter':5 -[ RECORD 7 ]---------------------------------------------------- doc | I slit sheets. doc_tsv | 'sheet':3 'slit':2 -[ RECORD 8 ]---------------------------------------------------- doc | I am the sleekest sheet slitter that ever slit sheets. doc_tsv | 'ever':8 'sheet':5,10 'sleekest':4 'slit':9 'slitter':6 -[ RECORD 9 ]---------------------------------------------------- doc | She slits the sheet she sits on. doc_tsv | 'sheet':4 'sit':6 'slit':2 

Wie soll der Index aufgebaut sein? Die direkte Verwendung des R-Baums ist keine Option, da unklar ist, wie ein "Begrenzungsrechteck" für Dokumente definiert werden soll. Wir können diesen Ansatz jedoch für Mengen modifizieren, einen sogenannten RD-Baum (RD steht für "Russian Doll"). Unter einer Menge wird in diesem Fall eine Menge von Lexemen verstanden, aber im Allgemeinen kann eine Menge eine beliebige sein.

Eine Idee von RD-Bäumen besteht darin, ein Begrenzungsrechteck durch eine Begrenzungsmenge zu ersetzen, dh eine Menge, die alle Elemente von untergeordneten Mengen enthält.

Es stellt sich eine wichtige Frage, wie Mengen in Indexzeilen dargestellt werden sollen. Am einfachsten ist es, alle Elemente der Menge aufzulisten. Dies könnte wie folgt aussehen:



Für den Zugriff über die Bedingung doc_tsv @@ to_tsquery('sit') könnten wir dann beispielsweise nur zu den Knoten absteigen, die das "sit" doc_tsv @@ to_tsquery('sit') enthalten:



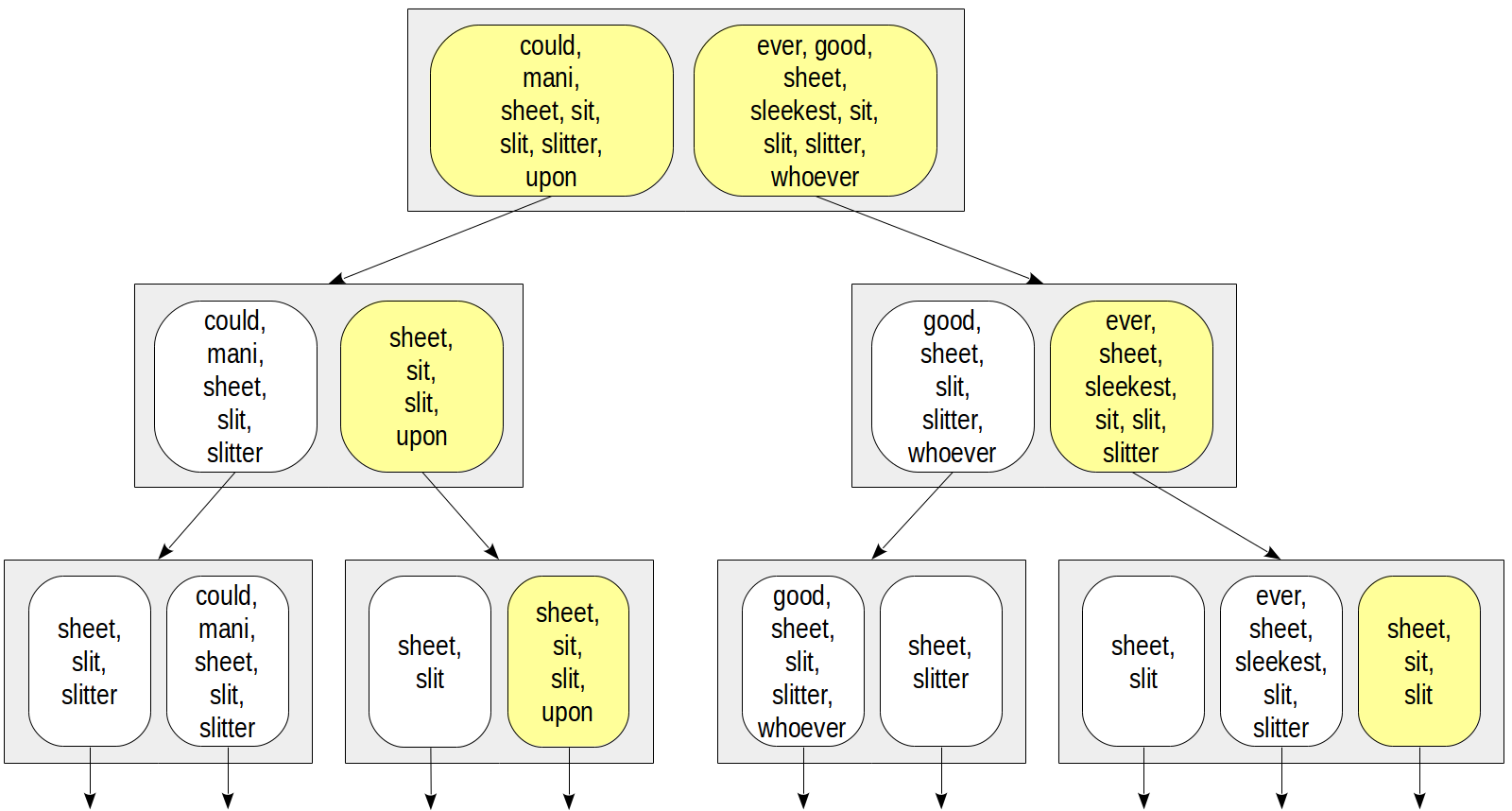
Diese Darstellung hat offensichtliche Probleme. Die Anzahl der Lexeme in einem Dokument kann sehr groß sein, sodass Indexzeilen eine große Größe haben und in TOAST gelangen, wodurch der Index weitaus weniger effizient wird. Selbst wenn jedes Dokument nur wenige eindeutige Lexeme enthält, kann die Vereinigung von Mengen dennoch sehr groß sein: Je höher der Stamm, desto größer die Indexzeilen.

Eine Darstellung wie diese wird manchmal verwendet, jedoch für andere Datentypen. Bei der Volltextsuche wird eine andere, kompaktere Lösung verwendet - ein sogenannter Signaturbaum . Die Idee ist allen bekannt, die sich mit Bloom-Filtern befasst haben.

Jedes Lexem kann mit seiner Signatur dargestellt werden : eine Bitfolge einer bestimmten Länge, bei der alle Bits bis auf eins Null sind. Die Position dieses Bits wird durch den Wert der Hash-Funktion des Lexems bestimmt (wir haben die Interna von Hash-Funktionen früher besprochen).

Die Dokumentensignatur ist das bitweise ODER der Signaturen aller Dokumentlexeme.

Nehmen wir die folgenden Signaturen von Lexemen an:

 könnte 1.000.000
 jemals 0001000
 gut 0000010
 mani 0000100
 Blatt 0000100
 schlankste 0100000
 sitzen 0010000
 Schlitz 0001000
 Slitter 0000001
 auf 0000010
 wer auch immer 0010000

Dann sind die Unterschriften der Dokumente wie folgt:

 Kann ein Blechschneider Blätter schneiden?  0001101
 Wie viele Blätter könnte ein Blattschneider schneiden?  1001101
 Ich schneide ein Blatt, ein Blatt, das ich schneide.  0001100
 Auf einem geschlitzten Laken sitze ich.  0011110
 Wer die Blätter schneidet, ist ein guter Blattschneider.  0011111
 Ich bin ein Blechschneider.  0000101
 Ich schneide Laken.  0001100
 Ich bin der glatteste Blattschneider, der jemals Blätter geschnitten hat.  0101101
 Sie schneidet das Blatt, auf dem sie sitzt.  0011100

Der Indexbaum kann wie folgt dargestellt werden:



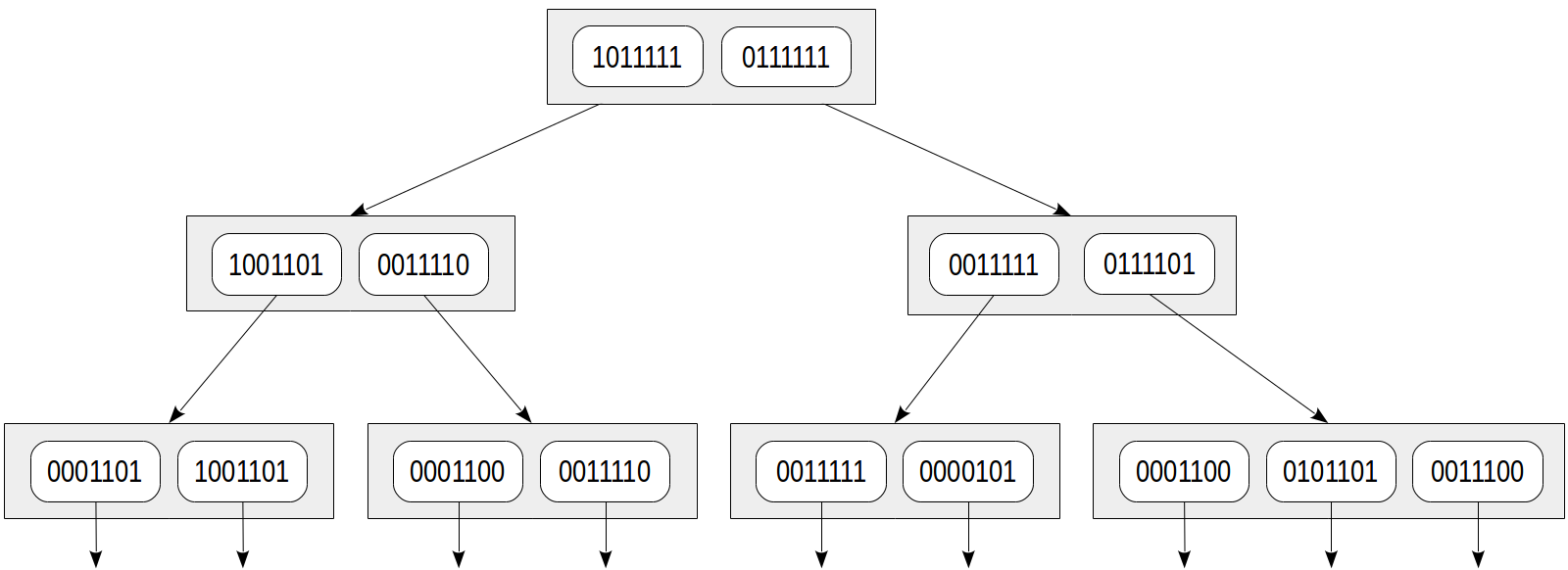
Die Vorteile dieses Ansatzes liegen auf der Hand: Indexzeilen sind gleich klein, und ein solcher Index ist kompakt. Ein Nachteil ist aber auch klar: Die Genauigkeit wird der Kompaktheit geopfert.

Betrachten wir die gleiche Bedingung doc_tsv @@ to_tsquery('sit') . Und berechnen wir die Signatur der Suchabfrage auf die gleiche Weise wie für das Dokument: 0010000 in diesem Fall. Die Konsistenzfunktion muss alle untergeordneten Knoten zurückgeben, deren Signaturen mindestens ein Bit aus der Abfragesignatur enthalten:



Vergleichen Sie mit der obigen Abbildung: Wir können sehen, dass der Baum gelb geworden ist, was bedeutet, dass während der Suche falsch positive Ergebnisse auftreten und übermäßige Knoten durchlaufen werden. Hier haben wir das "whoever" -Lexem aufgenommen, dessen Signatur leider mit der Signatur des "sit" -Lexems übereinstimmt. Es ist wichtig, dass im Muster keine falschen Negative auftreten können. Das heißt, wir werden die benötigten Werte sicher nicht verpassen.

Außerdem kann es vorkommen, dass verschiedene Dokumente auch die gleichen Signaturen erhalten: In unserem Beispiel sind unglückliche Dokumente "Ich schneide ein Blatt, ein Blatt, das ich schneide" und "Ich schneide Blätter" (beide haben die Signatur 0001100). Und wenn eine Blattindexzeile nicht den Wert von "tsvector" speichert, gibt der Index selbst falsch positive Ergebnisse aus. In diesem Fall fordert die Methode die Indizierungs-Engine natürlich auf, das Ergebnis mit der Tabelle erneut zu überprüfen, damit der Benutzer diese Fehlalarme nicht sieht. Die Sucheffizienz kann jedoch beeinträchtigt werden.

Tatsächlich ist eine Signatur in der aktuellen Implementierung 124 Byte groß, in den Abbildungen 7 Bit, sodass die oben genannten Probleme viel seltener auftreten als im Beispiel. In Wirklichkeit werden aber auch viel mehr Dokumente indiziert. Um die Anzahl der Fehlalarme der Indexmethode irgendwie zu verringern, wird die Implementierung etwas schwierig: Der indizierte "tsvector" wird in einer Blattindexzeile gespeichert, jedoch nur, wenn seine Größe nicht groß ist (etwas weniger als 1/16 von eine Seite, die für 8-KB-Seiten etwa ein halbes Kilobyte entspricht).

Beispiel

Um zu sehen, wie die Indizierung für tatsächliche Daten funktioniert, nehmen wir das Archiv der E-Mails "pgsql-hackers". Die im Beispiel verwendete Version enthält 356125 Nachrichten mit dem Versanddatum, dem Betreff, dem Autor und dem Text:

 fts=# select * from mail_messages order by sent limit 1; 

 -[ RECORD 1 ]------------------------------------------------------------------------ id | 1572389 parent_id | 1562808 sent | 1997-06-24 11:31:09 subject | Re: [HACKERS] Array bug is still there.... author | "Thomas G. Lockhart" <Thomas.Lockhart@jpl.nasa.gov> body_plain | Andrew Martin wrote: + | > Just run the regression tests on 6.1 and as I suspected the array bug + | > is still there. The regression test passes because the expected output+ | > has been fixed to the *wrong* output. + | + | OK, I think I understand the current array behavior, which is apparently+ | different than the behavior for v1.0x. + ... 

Hinzufügen und Ausfüllen der Spalte vom Typ "tsvector" und Erstellen des Index. Hier werden drei Werte in einem Vektor (Betreff, Autor und Nachrichtentext) zusammengefasst, um zu zeigen, dass das Dokument kein Feld sein muss, sondern aus völlig unterschiedlichen beliebigen Teilen bestehen kann.

 fts=# alter table mail_messages add column tsv tsvector; fts=# update mail_messages set tsv = to_tsvector(subject||' '||author||' '||body_plain); 

 NOTICE: word is too long to be indexed DETAIL: Words longer than 2047 characters are ignored. ... UPDATE 356125 

 fts=# create index on mail_messages using gist(tsv); 

Wie wir sehen können, wurde eine bestimmte Anzahl von Wörtern wegen zu großer Größe gelöscht. Der Index wird jedoch schließlich erstellt und kann Suchanfragen unterstützen:

 fts=# explain (analyze, costs off) select * from mail_messages where tsv @@ to_tsquery('magic & value'); 

  QUERY PLAN ---------------------------------------------------------- Index Scan using mail_messages_tsv_idx on mail_messages (actual time=0.998..416.335 rows=898 loops=1) Index Cond: (tsv @@ to_tsquery('magic & value'::text)) Rows Removed by Index Recheck: 7859 Planning time: 0.203 ms Execution time: 416.492 ms (5 rows) 

Wir können sehen, dass die Zugriffsmethode zusammen mit 898 Zeilen, die der Bedingung entsprechen, 7859 weitere Zeilen zurückgab, die durch erneutes Überprüfen mit der Tabelle herausgefiltert wurden. Dies zeigt einen negativen Einfluss des Genauigkeitsverlustes auf die Effizienz.

Interna

Um den Inhalt des Index zu analysieren, verwenden wir erneut die Erweiterung "gevel":

 fts=# select level, a from gist_print('mail_messages_tsv_idx') as t(level int, valid bool, a gtsvector) where a is not null; 

  level | a -------+------------------------------- 1 | 992 true bits, 0 false bits 2 | 988 true bits, 4 false bits 3 | 573 true bits, 419 false bits 4 | 65 unique words 4 | 107 unique words 4 | 64 unique words 4 | 42 unique words ... 

Werte des speziellen Typs "gtsvector", die in Indexzeilen gespeichert sind, sind tatsächlich die Signatur und möglicherweise die Quelle "tsvector". Wenn der Vektor verfügbar ist, enthält die Ausgabe die Anzahl der Lexeme (eindeutige Wörter), andernfalls die Anzahl der wahren und falschen Bits in der Signatur.

Es ist klar, dass im Wurzelknoten die Signatur zu "allen" degeneriert ist, dh eine Indexebene wurde absolut nutzlos (und eine weitere wurde mit nur vier falschen Bits fast nutzlos).

Eigenschaften

Schauen wir uns die Eigenschaften der GiST-Zugriffsmethode an (Abfragen wurden früher bereitgestellt ):

  amname | name | pg_indexam_has_property --------+---------------+------------------------- gist | can_order | f gist | can_unique | f gist | can_multi_col | t gist | can_exclude | t 

Das Sortieren von Werten und eindeutige Einschränkungen werden nicht unterstützt. Wie wir gesehen haben, kann der Index auf mehreren Spalten aufgebaut und in Ausschlussbeschränkungen verwendet werden.

Die folgenden Indexschicht-Eigenschaften sind verfügbar:

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | f 

Und die interessantesten Eigenschaften sind die der Säulenschicht. Einige der Eigenschaften sind unabhängig von Operatorklassen:

  name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f search_array | f search_nulls | t 

(Die Sortierung wird nicht unterstützt. Der Index kann nicht zum Durchsuchen eines Arrays verwendet werden. NULL-Werte werden unterstützt.)

Die beiden verbleibenden Eigenschaften "distance_orderable" und "returnable" hängen jedoch von der verwendeten Operatorklasse ab. Zum Beispiel erhalten wir für Punkte:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | t returnable | t 

Die erste Eigenschaft gibt an, dass der Entfernungsoperator für die Suche nach nächsten Nachbarn verfügbar ist. Und der zweite besagt, dass der Index nur für den Index-Scan verwendet werden kann. Obwohl Blattindexzeilen Rechtecke anstelle von Punkten speichern, kann die Zugriffsmethode das zurückgeben, was benötigt wird.

Die folgenden Eigenschaften gelten für Intervalle:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | t 

Für Intervalle ist die Distanzfunktion nicht definiert und daher ist die Suche nach nächsten Nachbarn nicht möglich.

Und für die Volltextsuche erhalten wir:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | f 

Die Unterstützung des Nur-Index-Scans ist verloren gegangen, da Blattzeilen nur die Signatur ohne die Daten selbst enthalten können. Dies ist jedoch ein geringfügiger Verlust, da sich ohnehin niemand für den Wert vom Typ "tsvector" interessiert: Dieser Wert wird zur Auswahl von Zeilen verwendet, während der Quelltext angezeigt werden muss, aber dennoch im Index fehlt.

Andere Datentypen

Abschließend werden einige weitere Typen erwähnt, die derzeit von der GiST-Zugriffsmethode unterstützt werden, zusätzlich zu den bereits diskutierten geometrischen Typen (am Beispiel von Punkten), Intervallen und Volltextsucharten.

Bei Standardtypen ist dies der Typ " inet " für IP-Adressen. Der Rest wird durch Erweiterungen hinzugefügt:

• cube bietet den Datentyp "cube" für mehrdimensionale Cubes. Für diesen Typ wird ebenso wie für geometrische Typen in einer Ebene die GiST-Operatorklasse definiert: R-Baum, der die Suche nach nächsten Nachbarn unterstützt.
  
• seg bietet den Datentyp "seg" für Intervalle mit Grenzen, die mit einer bestimmten Genauigkeit angegeben wurden, und unterstützt den GiST-Index für diesen Datentyp (R-Tree).
  
• intarray erweitert die Funktionalität von Integer-Arrays und fügt ihnen GiST-Unterstützung hinzu. Es sind zwei Operatorklassen implementiert: "gist__int_ops" (RD-Baum mit vollständiger Darstellung der Schlüssel in Indexzeilen) und "gist__bigint_ops" (Signatur-RD-Baum). Die erste Klasse kann für kleine Arrays verwendet werden, die zweite für größere Arrays.
  
• ltree fügt den Datentyp "ltree" für baumartige Strukturen und die GiST-Unterstützung für diesen Datentyp (RD-Baum) hinzu.
  
• pg_trgm fügt eine spezielle Operatorklasse "gist_trgm_ops" zur Verwendung von Trigrammen bei der Volltextsuche hinzu. Dies ist jedoch zusammen mit dem GIN-Index weiter zu erörtern.
  

Lesen Sie weiter .