Ich erinnere mich an eine wichtige Schlussfolgerung aus den vorhergehenden Teilen. Für ein zyklisches sequentielles Verhalten, das nicht mehrere Signale enthält (mehr als zweimaliges Umschalten eines Zyklus), kann die minimale logische Funktion jedes Signals in der folgenden Form dargestellt werden (natürlich ohne CSC-Konflikte):
1)
Dabei ist a * b * ... * c der Implikant einer oder mehrerer Variablen. g + h + ... + i - Dies ist möglicherweise eine leere Menge von Implikanten, die aus einer Variablen bestehen. x * f ist ein Implantat aus 2 Variablen, deren Vorhandensein in minimaler Form nicht erforderlich ist. Alle Variablen außer x können in direkter und inverser Form in die Formel aufgenommen werden, abhängig von der Anordnung der Vorzeichen der entsprechenden Ereignisse. Alle Variablen werden streng einmal als Argumente in die Formel aufgenommen.
Bevor wir fortfahren, werden wir uns ein Phänomen wie die Zersetzung genauer ansehen. Zuallererst ist die Zerlegung von Interesse, wodurch die Selbstsynchronisation erhalten bleibt. Beim Zerlegen einer logischen NOT-AND-OR-Funktion kann man als neues Element unterscheiden:
a) ein oder mehrere Implikanten,
b) mehrere Signale (Variablen) eines Implantats,
c) Wechselrichter mit einem Eingang.
Zunächst betrachten wir einen Sonderfall der NOR AND-Funktion. Das Verhalten einer solchen logischen Funktion (x = a + b + c + d) für das betreffende Modell:
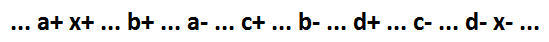
Sie kann mehrere Signale als separates Element unterscheiden.
Tatsächlich ist die Auswahl eines neuen Elements während der Zerlegung die Hinzufügung eines neuen Signals (f). Um ein korrektes Verhalten, Semimodularität und Selbstsynchronisation aufrechtzuerhalten, muss das Umschalten des neu hinzugefügten Signals f Konsequenzereignisse haben. Da die Zerlegung nur ein Element der Schaltung (in diesem Fall x) betrifft und die verbleibenden Elemente der Schaltung nicht beeinflusst, kann das Schalten des Signals f nur das Schalten des Signals x verursachen. Andernfalls würde die logische Funktion eines anderen Signals vom Signal f abhängen. Lassen Sie uns angesichts dieser Schlussfolgerung versuchen, mehrere Variablen außer der Variablen a als neues Element f hervorzuheben. Nehmen wir zum Beispiel die Variablen b und c. Sie bilden das logische Element f = b + c.
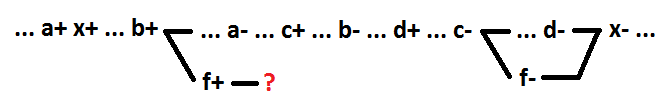
Wie zu sehen ist, ist es für das f + -Ereignis unmöglich, das Konsequenzereignis zu bestimmen, ohne die Richtigkeit des Verhaltens zu verletzen. Jede Gruppe von Signalen, die die Variable a nicht enthält, kann nicht als separates Element zugewiesen werden, während die Selbstsynchronisation beibehalten wird.
Ein Signal wie in diesem Beispiel wird als Einschalten bezeichnet. Im allgemeinen Fall ist das Schaltsignal für die Funktion ODER (UND) ein Signal. Wenn Sie es auf 1 (0) schalten, ändert sich der Wert der Funktion von 0 auf 1 (von 1 auf 0). Um die Selbstsynchronisation während der Zerlegung der logischen Funktion ODER (UND) bei der Auswahl eines neuen Elements aufrechtzuerhalten, müssen Sie das Schaltsignal verwenden. Bei der Auswahl eines neuen Elements müssen auch nur die Signale verwendet werden, die eine verbundene Kette bilden (im folgenden Beispiel a + b). x = f + c + d, f = a + b.
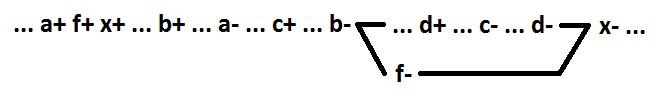
Bei Verwendung von a + b + d-Signalen bleibt die Selbstsynchronisation nicht erhalten.
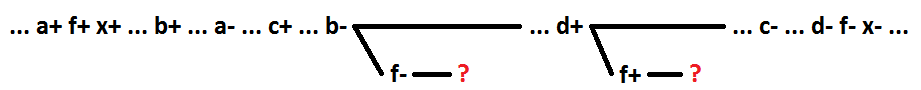
Für sequentielles Verhalten ohne mehrere Signale während der Zerlegung der logischen Funktion OR (I) stellt das Hervorheben der ersten paar im Prozess der Bereitstellung der Signale ausgehend von dem, das enthält, als neues Element sicher, dass die Schaltung selbstsynchronisiert ist.
Betrachten Sie nun die Nicht-ODER-Funktion (x =! A +! B). Als separates Element (f) können wir unter Beibehaltung der Selbstsynchronität nur den Eingangswechselrichter auswählen, der dem Schaltsignal entspricht (x = f +! B, f =! A). Die Trennung anderer Eingangswechselrichter als separates Element führt zu einer Verletzung der Selbstsynchronisation.
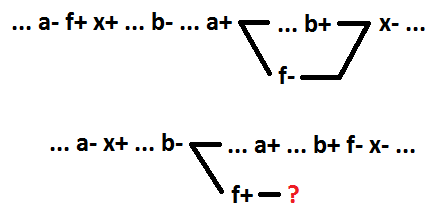
Fahren wir mit der UND-ODER-Funktion fort. In ähnlicher Weise definieren wir als Schaltsignal für die ODER-Funktion das Schaltimplikant für die UND-ODER-Funktion. Dies ist ein Implikant, dessen Änderung von 0 auf 1 zu einer Änderung des Werts der Funktion von 0 auf 1 führt. Ähnlich wie es für die ODER-Funktion herausgefunden wurde, für sequentielles Verhalten ohne mehrere Signale beim Zerlegen der logischen UND-ODER-Funktion, wobei die ersten paar als neues Element ausgewählt werden Während des Bereitstellungsprozesses garantiert der Implikant, beginnend mit der Einbeziehung, die Wahrung der Selbstsynchronisation der Schaltung. Andernfalls wird die Selbstsynchronisation unterbrochen. Im folgenden Beispiel ist vor der Zerlegung x = a * b + c. Nach der Zersetzung ist x = f + c, f = a * b.
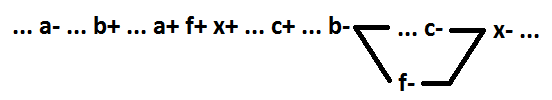
Für die UND-ODER-Funktion betrachten wir die Auswahl als ein neues Element mehrerer Variablen, die in demselben Implikanten enthalten sind. Es werden nur minimale Funktionen berücksichtigt. Nachfolgend sind alle möglichen Optionen für das Beispiel der Funktion x = a * b * c + d aufgeführt (für Option 4 - x = a * b * c + d + e, für Option 6 - x = a * b * c * d + e) . Das hervorgehobene Element ist f = a * b.

In Option 1 ist das Umschalten eines der zugewiesenen Signale (a +) die Ursache für das x + -Ereignis. In Option 2 ist das Umschalten eines der zugewiesenen Signale (a-) die Ursache für das x-Ereignis. In den Optionen 3 und 4 befindet sich das Umschalten eines der zugewiesenen Signale (a + bzw. a-) zwischen den Ereignissen x + und x- und ist nicht die Ursache für das Ereignis x-. Option 5 ist ein Sonderfall von Option 4, wenn der Implikant, in dem die Signale zugeordnet sind, inklusive ist. Die verbleibende Option 6 - alle Schaltvorgänge der zugewiesenen Signale befinden sich zwischen den Ereignissen x- und x + und sind nicht die Ursachen für das Ereignis x +.
Wie Sie sehen können, kann das f-Ereignis in den Optionen 1 und 6 nicht richtig positioniert werden. Solche Transformationen sind keine Zerlegung unter Wahrung der Selbstsynchronisation. In den Optionen 2, 3 und 4 bleibt die Selbstsynchronisation erhalten. Der Wert der Funktion x unterscheidet sich jedoch von f * c + d (f * c + d + e für 4 Optionen). Für 2 Optionen - x = f * (d + c), für 3 Optionen x = c * x + d *! F + x *! F, für 4 Optionen x = (f + d) * (e + c). Solche Transformationen sind keine Zerlegungen.
Nur Option 5 ist eine Zerlegung unter Beibehaltung der Selbstsynchronisation (x = f * c + d). In diesem Fall werden als separates Element im Einschlussimplikanten die ersten mehreren Signale ausgehend vom Einschluss ausgewählt (das Signal einschließlich des Implikanten And ist dasselbe wie das Signal einschließlich der And-Funktion). Wie oben gezeigt, wird ein ähnliches Ergebnis jedoch in zwei Schritten erzielt. Zunächst wird der Einschluss des Implantats hervorgehoben. Im zweiten Schritt werden die ersten Signale im neuen Element ausgewählt, beginnend mit dem Schaltsignal.
Fahren wir mit der NON-AND-OR-Funktion fort. Lassen Sie uns den Eingangswechselrichter als separates Element herausgreifen. Das Signal a entspricht dem Eingang des Elements x, an das ein dedizierter Eingangswechselrichter angeschlossen ist (f =! A).
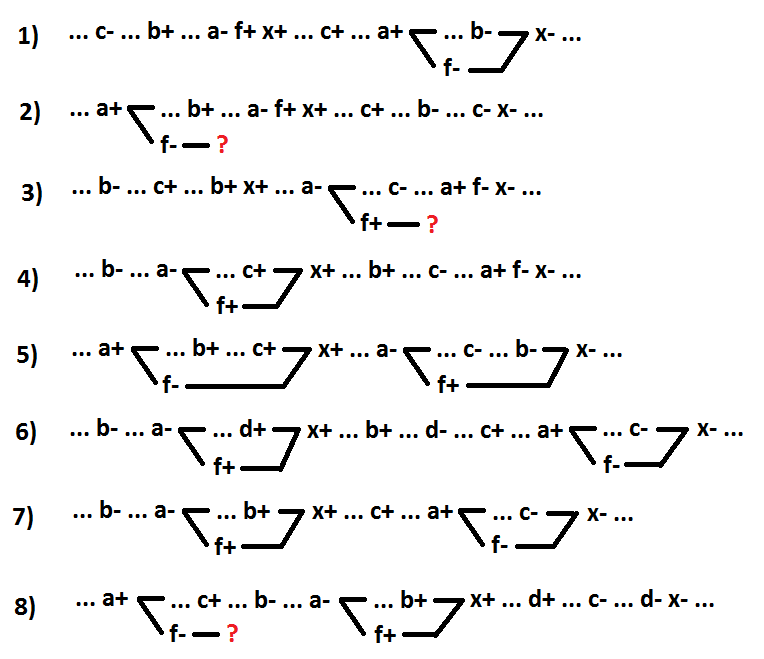
Optionen 1 und 2 - Schaltsignal a ist die Ursache des Ereignisses x + (1 - x =! A + b * c, 2 - x = b *! A + c). Optionen 3 und 4 - Umschalten des Signals a ist die Ursache des Ereignisses x- (3 - x =! A + b * c, 4 - x =! A * b + c). Optionen 5 und 6 - Das Umschalten des Signals a befindet sich zwischen den Ereignissen x + und x- und ist nicht die Ursache des Ereignisses x- (5 - x = b *! A + c, 6 - x =! A * b + d + c). Option 7 ist ein Sonderfall von Option 6, wenn Signal a ein Schaltsignal mit Implikanten ist (x =! A * b + c). Die verbleibende Option 8 - alle Signalschaltungen a befinden sich zwischen den Ereignissen x- und x + und sind nicht die Ursachen für das Ereignis x + (x = c *! A * b + d).
Wie Sie sehen können, sind die Optionen 2, 3 und 8 keine Zerlegung unter Beibehaltung der Selbstsynchronisation, da es unmöglich ist, die Signalumschaltung f korrekt zu positionieren. Für Option 4 ist nach der Konvertierung x = f * (c + b). Für Option 5 ist nach der Konvertierung x = c *! F +! F * x + b * x. Für Option 6 ist nach der Umrechnung x = (f + c) * (d + b). Diese Transformationen (Optionen 4, 5 und 6) sind keine Zerlegungen. Für Option 7 ist nach der Konvertierung x = f * b + c. Option 7 ist eine Zerlegung unter Beibehaltung der Selbstsynchronisation. In diesem Fall wird ein Wechselrichter, der dem Schaltsignal einschließlich der Implantate entspricht, als separates Element zugeordnet. Ein ähnliches Ergebnis wird in zwei Schritten unter Verwendung der obigen Transformationen erzielt. Zuerst wird der Einschluss des Implikanten hervorgehoben, dann wird ihm der Eingangsinverter des Einschaltsignals zugewiesen. Für Option 1 ist nach der Konvertierung x = f + b * c. Option 1 ist auch eine Zerlegung unter Beibehaltung der Selbstsynchronisation. Dies ist ein Sonderfall von Option 7, wenn der Einschluss des Implikanten aus einem Signal besteht.
Wir systematisieren die erzielten Ergebnisse. Für das betrachtete Modell sind beim Zerlegen einer logischen NOT-AND-OR-Funktion zur Aufrechterhaltung der Selbstsynchronität nur die folgenden Transformationen möglich - Zuordnung als separates Element:
1 - eines oder mehrere, beginnend mit dem inklusiven, überlappenden Implikanten (ein Sonderfall - für die Funktion der NON-OR-Auswahl mehrerer überlappender Signale, beginnend mit dem inklusive);
2 - im Einschluss implizieren mehrere, beginnend mit dem Einschluss, überlappende Signale;
3 - Eingangswechselrichter entsprechend dem Schaltsignal einschließlich Implikanten (ein Sonderfall - für die Funktion der Nicht-ODER-Auswahl des Eingangswechselrichters entsprechend dem Schaltsignal).
Diese Transformationen erlauben es dem Implikanten nicht, inklusiv zu sein, wenn es nicht vor der Transformation war. Daher die Schlussfolgerung: Wenn eine logische Funktion einen Implikanten enthält, der aus mehr als einem Signal besteht und nicht inklusive ist, kann eine solche Funktion nicht unter Verwendung einer Zerlegung fragmentiert werden, die die Selbstsynchronisation bis zu Elementen mit zwei Eingängen bewahrt. Jede logische NOT-AND-OR-Funktion, in der mehr als eine Variable nur einen inklusiven Implikanten enthält, kann mithilfe einer Zerlegung, die die Selbstsynchronisation bewahrt, in Elemente mit zwei Eingaben (2AND-NOT, 2OR-NOT) aufgeteilt werden.
Schritt 1 - Wenn das logische Element nur einen Implikanten enthält (oder alle Implikanten aus einer Variablen bestehen), fahren Sie mit Schritt 3 fort, andernfalls fahren Sie mit Schritt 2 fort.
Schritt 2 - Wählen Sie alle Implantate bis auf eines als separates Element aus, beginnend mit dem Einschluss. Als nächstes arbeiten wir mit dem neu erhaltenen Artikel. Fahren Sie mit Schritt 1 fort.
Schritt 3 - Wenn das Element aus zwei Variablen besteht, fahren Sie mit Schritt 5 fort, andernfalls fahren Sie mit Schritt 4 fort.
Schritt 4 - Wir wählen alle Variablen außer einer als separates Element aus, beginnend mit der Aufnahme. Als nächstes arbeiten wir mit dem neu erhaltenen Artikel. Fahren Sie mit Schritt 3 fort.
Schritt 5 - gilt für alle empfangenen Elemente mit zwei Eingaben.
Schritt 5.1 - Wenn sich die Eingangswechselrichter an beiden Eingängen befinden, konvertieren wir das Element in Dual.
Schritt 5.2 - Wenn der Eingangswechselrichter eins ist und einem Signal entspricht, das nicht eingeschaltet wird, wandeln wir das Element in ein duales um.
Schritt 5.3 - Der Eingangswechselrichter, falls vorhanden, wird als separates Element hervorgehoben. Zerkleinerung abgeschlossen.
Nun zurück zu Formel 1 am Anfang des Textes. Wenn der Implikant x * f nicht im logischen Ausdruck enthalten ist, sieht die Funktion folgendermaßen aus: x = a * b * c + g + h + i. Ihr Verhalten:
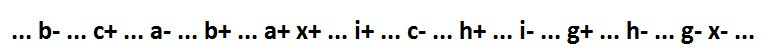
Wie Sie sehen können, ist der einzige Implikant von mehr als einer Variablen (a * b * c) inklusive. Und diese Funktion kann mit Hilfe der Zerlegung auf die minimalen Komponenten fragmentiert werden, während die Selbstsynchronisation erhalten bleibt.
Wenn der Implikant x * f in einem logischen Ausdruck vorhanden ist, sieht die Funktion folgendermaßen aus: x = a * b * c + x * f + g + h + i. Ihr Verhalten:
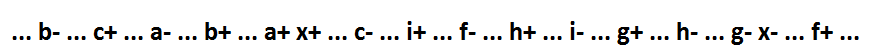
Der nicht inklusive x * f-Implikant besteht aus mehr als einer Variablen. Eine solche Funktion kann nicht fragmentiert werden, während die Selbstsynchronisation aufrechterhalten wird. Wir wenden jedoch eine Transformation an, die die Selbstsynchronisation bewahrt: Addieren Sie das Signal y - dual zum Signal x. Durch Hinzufügen des Signals y wird nur die Funktion des Signals x und des Signals geändert, deren Umschaltung eine Folge des Ereignisses x- war (die Variable x wird durch die Variable y ersetzt).
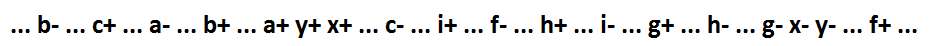
Jetzt ist x = (f + i + h + g) * y, y = c * b * a + x. Die Implikanten f + i + h + g und c * b * a einschließlich bzw. der Funktionen x und y können unter Beibehaltung der Selbstsynchronisation auf die minimalen Komponenten fragmentiert werden.
Ein vereinfachtes Verhaltensmodell (ohne Parallelität, Auswahl und mehrere Signale) ermöglicht es Ihnen, Eigenschaften zu identifizieren, die binären Prozessen von Natur aus eigen sind. Die Synthese von selbstsynchronen Schaltungen auf minimaler Basis ist ein natürliches Phänomen, das kein Design erfordert.