In einem früheren Artikel habe ich darauf hingewiesen, wie weit verbreitet das Problem des Missbrauchs des t-Kriteriums in wissenschaftlichen Veröffentlichungen ist (und dies ist nur aufgrund ihrer Offenheit möglich, und welcher Müll entsteht, wenn er in Kursen, Berichten, Schulungsaufgaben usw. verwendet wird - ist unbekannt). . Um dies zu diskutieren, sprach ich über die Grundlagen der Varianzanalyse und das vom Forscher selbst festgelegte Signifikanzniveau α. Für ein umfassendes Verständnis des Gesamtbildes der statistischen Analyse ist es jedoch erforderlich, eine Reihe wichtiger Dinge hervorzuheben. Und das grundlegendste davon ist das Konzept des Irrtums.
Fehler und falsche Anwendung: Was ist der Unterschied?
Jedes physische System enthält eine Art Fehler, Ungenauigkeit. In der verschiedensten Form: die sogenannte Toleranz - der Größenunterschied verschiedener Produkte des gleichen Typs; nichtlineare Charakteristik - wenn ein Gerät oder eine Methode innerhalb bestimmter Grenzen nach einem bekannten Gesetz misst und dann nicht mehr anwendbar ist; Diskretion - wenn wir technisch nicht in der Lage sind, eine reibungslose Ausgabeeigenschaft zu gewährleisten.
Gleichzeitig gibt es einen rein menschlichen Fehler - falsche Verwendung von Geräten, Instrumenten, mathematischen Gesetzen. Es gibt einen grundlegenden Unterschied zwischen dem dem System innewohnenden Fehler und dem Fehler bei der Anwendung dieses Systems. Es ist wichtig, diese beiden Konzepte, die als das gleiche Wort „Fehler“ bezeichnet werden, zu unterscheiden und nicht miteinander zu verwechseln. In diesem Artikel bevorzuge ich das Wort "Fehler", um die Eigenschaften des Systems zu kennzeichnen, und "falsche Verwendung" - für seine fehlerhafte Verwendung.
Das heißt, der Fehler des Lineals entspricht der Toleranz der Ausrüstung, wodurch Striche auf die Leinwand gelegt werden. Ein Fehler im Sinne einer falschen Verwendung wäre die Verwendung beim Messen der Details einer Uhr. Der Fehler des Steelyards ist darauf geschrieben und beträgt ungefähr 50 Gramm, und der Missbrauch des Steelyards würde darin bestehen, einen 25-kg-Beutel darauf zu wiegen, der die Feder vom Bereich des Hookeschen Gesetzes zum Bereich der plastischen Verformungen ausdehnt. Der Fehler eines Rasterkraftmikroskops beruht auf seiner Diskretion - Sie können Objekte nicht mit einer Sonde "berühren", die kleiner als ein Durchmesser von einem Atom ist. Es gibt jedoch viele Möglichkeiten, Daten zu missbrauchen oder falsch zu interpretieren. Usw.
Welche Art von Fehler hat dies bei statistischen Methoden? Und dieser Fehler ist genau das berüchtigte Signifikanzniveau α.
Fehler der ersten und zweiten Art
Ein Fehler im mathematischen Apparat der Statistik ist das Bayes'sche probabilistische Wesen selbst. Im letzten Artikel habe ich bereits erwähnt, worauf statistische Methoden basieren: Bestimmen des Signifikanzniveaus α als die größte zulässige Wahrscheinlichkeit, die Nullhypothese illegal abzulehnen, und der Forscher, diesen Wert dem Forscher unabhängig zuzuweisen.
Sehen Sie diese Konvention bereits? Tatsächlich gibt es bei den Kriterienmethoden keine bekannte mathematische Strenge. Die Mathematik arbeitet mit probabilistischen Merkmalen.
Und hier kommt ein weiterer Punkt, an dem eine Fehlinterpretation eines Wortes in einem anderen Kontext möglich ist. Es ist notwendig, zwischen dem Konzept der Wahrscheinlichkeit und der tatsächlichen Implementierung eines Ereignisses zu unterscheiden, ausgedrückt in der Verteilung der Wahrscheinlichkeit. Bevor wir beispielsweise mit einem unserer Experimente beginnen, wissen wir nicht, welchen Wert wir dadurch erhalten. Es gibt zwei mögliche Ergebnisse: Wenn wir einen bestimmten Wert aus dem Ergebnis gemacht haben, werden wir ihn entweder wirklich bekommen oder nicht. Es ist logisch, dass die Wahrscheinlichkeit beider Ereignisse 1/2 beträgt. Die im vorherigen Artikel gezeigte Gaußsche Kurve zeigt jedoch
die Wahrscheinlichkeitsverteilung , mit der wir den Zufall richtig erraten.
Sie können dies anhand eines Beispiels deutlich veranschaulichen. Lassen Sie uns 600 Mal zwei Würfel werfen - regelmäßig und betrügerisch. Wir erhalten folgende Ergebnisse:

Vor dem Experiment ist für beide Würfel der Verlust eines Gesichts gleich wahrscheinlich - 1/6. Nach dem Experiment erscheint jedoch die Essenz des Betrugswürfels, und wir können sagen, dass die Wahrscheinlichkeitsdichte der sechs darauf fallenden sechs 90% beträgt.
Ein weiteres Beispiel, über das Chemiker, Physiker und alle, die sich für Quanteneffekte interessieren, Bescheid wissen, sind Atomorbitale. Theoretisch kann ein Elektron im Raum „verschmiert“ und fast überall lokalisiert werden. In der Praxis gibt es jedoch Bereiche, in denen dies in 90 Prozent oder mehr Fällen der Fall sein wird. Diese Raumregionen, die von einer Oberfläche mit einer Wahrscheinlichkeitsdichte eines Elektrons von 90% gebildet werden, sind klassische Atomorbitale in Form von Kugeln, Hanteln usw.
Indem wir das Signifikanzniveau unabhängig einstellen, stimmen wir dem in seinem Namen beschriebenen Fehler bewusst zu. Aus diesem Grund kann kein einziges Ergebnis als „absolut zuverlässig“ angesehen werden - unsere statistischen Schlussfolgerungen enthalten immer eine gewisse Ausfallwahrscheinlichkeit.
Ein Fehler, der durch Bestimmen des Signifikanzniveaus α formuliert wird, wird als
Fehler der ersten Art bezeichnet . Es kann als „falscher Alarm“ oder genauer gesagt als falsch positives Ergebnis definiert werden. Was bedeuten die Worte „fälschlicherweise die Nullhypothese ablehnen“? Dies bedeutet, dass die beobachteten Daten fälschlicherweise als signifikante Unterschiede zwischen den beiden Gruppen angesehen werden. Eine falsche Diagnose über das Vorhandensein der Krankheit zu stellen, der Welt eine neue Entdeckung zu offenbaren, die es tatsächlich nicht gibt - dies sind Beispiele für Fehler der ersten Art.
Aber sollte es dann falsch negative Ergebnisse geben? Ganz richtig, und sie werden
Fehler der zweiten Art genannt . Beispiele sind eine vorzeitige Diagnose oder Enttäuschung als Ergebnis der Studie, obwohl sie tatsächlich wichtige Daten enthält. Fehler der zweiten Art werden seltsamerweise durch den Buchstaben β angezeigt. Dieses Konzept selbst ist für die Statistik jedoch nicht so wichtig wie die Zahl 1-β. Die Zahl 1-β wird als
Potenz des Kriteriums bezeichnet und kennzeichnet, wie Sie vielleicht erraten haben, die Fähigkeit des Kriteriums, ein signifikantes Ereignis nicht zu verpassen.
Der Inhalt statistischer Fehlermethoden der ersten und zweiten Art ist jedoch nicht nur deren Einschränkung. Das Konzept dieser Fehler kann direkt in der statistischen Analyse verwendet werden. Wie?
ROC-Analyse
Die ROC-Analyse (anhand der Betriebscharakteristik des Empfängers) ist eine Methode zur Quantifizierung der Anwendbarkeit eines bestimmten Attributs auf eine binäre Klassifizierung von Objekten. Einfach ausgedrückt, wir können eine Möglichkeit finden, kranke Menschen von gesunden Menschen, Katzen von Hunden, schwarze von weißen zu unterscheiden und dann die Gültigkeit dieser Methode zu überprüfen. Schauen wir uns noch einmal ein Beispiel an.
Lassen Sie Sie ein angehender Forensiker sein und entwickeln Sie einen neuen Weg, um diskret und eindeutig festzustellen, ob eine Person ein Krimineller ist. Sie haben ein quantitatives Zeichen gefunden: die kriminellen Neigungen von Menschen anhand der Häufigkeit ihres Zuhörens zu Mikhail Krug zu bewerten. Aber wird Ihr Symptom angemessene Ergebnisse liefern? Lass es uns richtig machen.
Sie benötigen zwei Personengruppen, um Ihre Kriterien zu validieren: normale Bürger und Kriminelle. Nehmen wir in der Tat an, dass die durchschnittliche jährliche Zeit, die sie Mikhail Krug zuhören, unterschiedlich ist (siehe Abbildung):
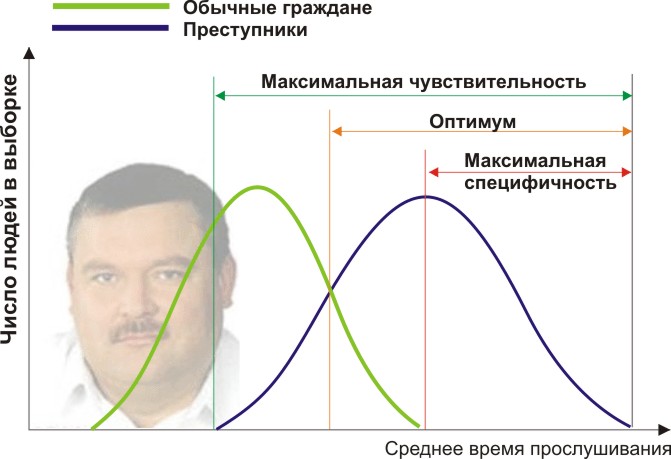
Hier sehen wir, dass sich unsere Stichproben durch das quantitative Vorzeichen der Hörzeit schneiden. Jemand hört sich den Kreis spontan im Radio an, ohne Verbrechen zu begehen, und jemand verstößt gegen das Gesetz, indem er andere Musik hört oder sogar taub ist. Welche Randbedingungen haben wir? Die ROC-Analyse führt in die Konzepte der Selektivität (Sensitivität) und Spezifität ein. Sensitivität ist definiert als die Fähigkeit, alle für uns interessanten Punkte (in diesem Beispiel Kriminelle) und die Spezifität zu identifizieren - nichts Falsch Positives zu erfassen (gewöhnliche Einwohner nicht zu verdächtigen). Wir können einige kritische quantitative Merkmale festlegen, die einige von den anderen trennen (orange) und von maximaler Empfindlichkeit (grün) bis maximaler Spezifität (rot) reichen.
Schauen wir uns das folgende Diagramm an:

Durch Verschieben des Werts unseres Attributs ändern wir das Verhältnis von falsch positiven und falsch negativen Ergebnissen (den Bereich unter den Kurven). Auf die gleiche Weise können wir Empfindlichkeit = Position definieren. Res-t / (Positiv Res-t + falsch-negativ. Res-t) und Spezifität = Neg. Res-t / (Negativ Res-t + falsch positiv. Res-t).
Vor allem aber können wir das Verhältnis von positiven zu falsch positiven Ergebnissen über den gesamten Wertebereich unseres quantitativen Attributs bewerten, das unsere gewünschte ROC-Kurve ist (siehe Abbildung):

Und wie verstehen wir aus dieser Grafik, wie gut unser Attribut ist? Berechnen Sie ganz einfach die Fläche unter der Kurve (AUC, Fläche unter der Kurve). Die gestrichelte Linie (0,0; 1,1) bedeutet die vollständige Übereinstimmung der beiden Stichproben und ein völlig bedeutungsloses Kriterium (die Fläche unter der Kurve beträgt 0,5 des gesamten Quadrats). Die Konvexität der ROC-Kurve zeigt jedoch nur die Perfektion des Kriteriums an. Wenn es uns gelingt, ein solches Kriterium zu finden, dass sich die Stichproben überhaupt nicht schneiden, nimmt der Bereich unter der Kurve den gesamten Graphen ein. Im Allgemeinen wird das Merkmal als gut angesehen, so dass eine Probe zuverlässig von einer anderen getrennt werden kann, wenn die AUC> 0,75 bis 0,8 beträgt.
Mit dieser Analyse können Sie eine Vielzahl von Problemen lösen. Nachdem Sie entschieden haben, dass zu viele Hausfrauen wegen Michael Krug unter Verdacht stehen und außerdem gefährliche Wiederholungstäter, die Noggano hören, übersehen werden, können Sie dieses Kriterium ablehnen und ein anderes entwickeln.
Die ROC-Analyse hat sich als ein Weg zur Verarbeitung von Funksignalen und zur Identifizierung von „Freunden oder Feinden“ nach einem Angriff auf Pearl Harbor herausgestellt (daher der seltsame Name für Empfängereigenschaften) und hat in der biomedizinischen Statistik eine breite Anwendung für die Analyse, Validierung, Erstellung und Charakterisierung von Biomarker-Panels gefunden usw. Es ist flexibel zu bedienen, wenn es auf einer soliden Logik basiert. Sie können beispielsweise Indikationen für die medizinische Untersuchung von Kernpatienten im Ruhestand entwickeln, indem Sie ein hochspezifisches Kriterium anwenden, die Effizienz der Erkennung von Herzerkrankungen erhöhen und Ärzte nicht mit unnötigen Patienten überlasten. Und während einer gefährlichen Epidemie eines bisher unbekannten Virus können Sie im Gegenteil ein hochselektives Kriterium entwickeln, damit niemand sonst buchstäblich der Impfung entgeht.
Bei der Beschreibung validierter Kriterien sind wir auf Fehler beider Art und deren Sichtbarkeit gestoßen. Ausgehend von diesen logischen Grundlagen können wir nun eine Reihe falscher stereotyper Beschreibungen der Ergebnisse zerstören. Einige falsche Formulierungen erfassen unseren Geist, oft verwirrt durch ihre ähnlichen Wörter und Konzepte und auch wegen der sehr geringen Aufmerksamkeit, die einer falschen Interpretation geschenkt wird. Dies muss möglicherweise separat geschrieben werden.