Delaunay-Triangulationsalgorithmus durch Sweeping-Line-Methode

Guten Tag!

In diesem Artikel werde ich detailliert den Algorithmus beschreiben, den ich erhalten habe, als ich die Idee verwendet habe, die gerade Linie zu fegen, um die Delaunay-Triangulation auf einer Ebene zu konstruieren. Es gibt einige Ideen, die ich nie getroffen habe, als ich Artikel über Triangulation gelesen habe.
Vielleicht findet sie auch jemand ungewöhnlich. Ich werde versuchen, alles in bester Tradition zu tun und die folgenden Dinge in die Geschichte aufzunehmen: eine Beschreibung der verwendeten Datenstrukturen, eine Beschreibung der Schritte des Algorithmus, einen Korrektheitsnachweis, Zeitschätzungen sowie einen Vergleich mit einem iterativen Algorithmus unter Verwendung des kD-Baums.

Definitionen und Erklärung des Problems

Triangulation

Sie sagen, dass die Triangulation für die Menge der Punkte in der Ebene angegeben wird, wenn einige Punktepaare durch eine Kante verbunden sind, jede endliche Fläche im resultierenden Diagramm ein Dreieck bildet, die Kanten sich nicht schneiden und das Diagramm die maximale Anzahl von Kanten aufweist.

Delaunay-Triangulation

Eine Delaunay-Triangulation ist eine Triangulation, bei der für jedes Dreieck keine Punkte aus der ursprünglichen Menge innerhalb des umschriebenen Kreises vorhanden sind.

Hinweis : Für einen bestimmten Satz von Punkten, in denen sich keine 4 Punkte auf demselben Kreis befinden, gibt es genau eine Delaunay-Triangulation.

Der Delaunay-Zustand

Es sei eine Triangulation auf die Menge der Punkte gegeben. Wir sagen, dass eine bestimmte Teilmenge von Punkten die Delaunay-Bedingung erfüllt, wenn die auf diese Teilmenge begrenzte Triangulation für ihn die Delaunay-Triangulation ist.

Kriterium für die Delaunay-Triangulation

Die Erfüllung der Delaunay-Bedingung für alle Punkte, die ein Viereck in einer Triangulation bilden, entspricht der Tatsache, dass diese Triangulation eine Delaunay-Triangulation ist.

Hinweis : Für nicht konvexe Vierecke ist die Delaunay-Bedingung immer erfüllt, und für konvexe Vierecke (deren Eckpunkte nicht auf demselben Kreis liegen) gibt es genau zwei mögliche Triangulationen (eine davon ist die Delaunay-Triangulation).

Die Aufgabe besteht darin, eine Delaunay-Triangulation für eine bestimmte Menge von Punkten zu erstellen.

Beschreibung des Algorithmus

Sichtbare Punkte und sichtbare Kanten

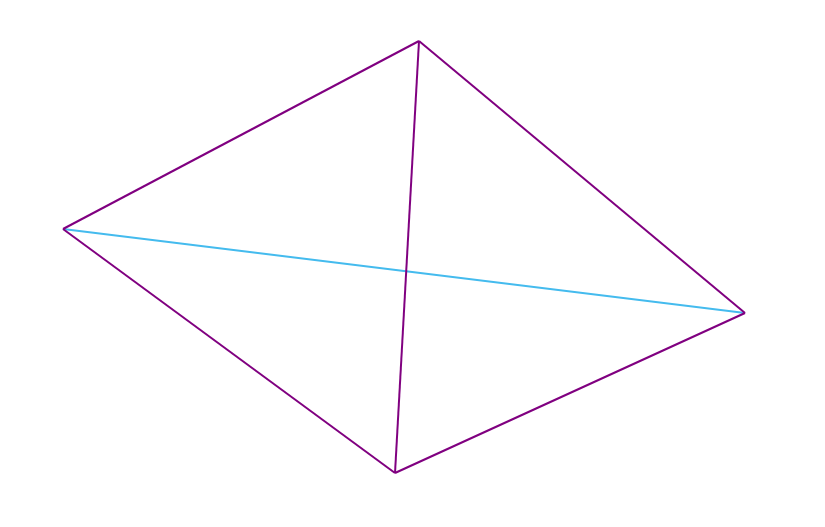
Es sei eine minimale konvexe Hülle (im Folgenden MBO) aus einer endlichen Menge von Punkten (Kanten, die einige der Punkte so verbinden, dass sie ein Polygon bilden, das alle Punkte der Menge enthält) und einem Punkt A gegeben, der außerhalb der Hülle liegt. Dann wird der Punkt der Ebene für Punkt A als sichtbar bezeichnet, wenn das Segment, das ihn mit Punkt A verbindet, das MBO nicht schneidet.

Eine MBO-Kante wird für Punkt A als sichtbar bezeichnet, wenn ihre Enden für A sichtbar sind.

Im folgenden Bild sind die für den roten Punkt sichtbaren Kanten rot markiert:

Hinweis : Die Delaunay-Triangulationskontur ist das MBO für die Punkte, auf denen sie aufgebaut ist.

Anmerkung 2 : Im Algorithmus bilden die für den hinzugefügten Punkt A sichtbaren Kanten eine Kette, dh mehrere MBO-Kanten in einer Reihe

Speichern der Triangulation im Speicher

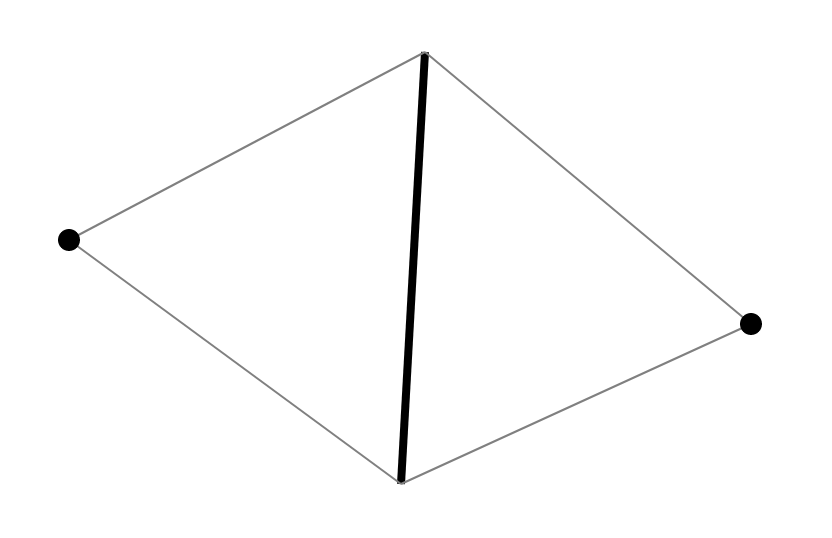
Es gibt einige Standardmethoden, die im Buch Skvortsov [1] gut beschrieben sind. Aufgrund der Besonderheiten des Algorithmus werde ich meine eigene Version anbieten. Da wir die 4-Gons auf den Delaunay-Zustand überprüfen wollen, betrachten wir ihre Struktur. Jedes Viereck in der Triangulation besteht aus 2 Dreiecken mit einer gemeinsamen Kante. Jede Kante hat genau 2 Dreiecke neben sich. Somit wird jedes Viereck in der Triangulation durch eine Kante und zwei Eckpunkte erzeugt, die der Kante in benachbarten Dreiecken gegenüberliegen.
Da zwei Dreiecke und ihre Nachbarschaft entlang der Kante und zwei Eckpunkte wiederhergestellt werden, können wir die Triangulation für alle diese Strukturen wiederherstellen. Dementsprechend wird vorgeschlagen, eine Kante mit zwei Eckpunkten in der Menge zu speichern und eine Suche entlang der Kante durchzuführen (ein geordnetes Paar von Eckpunkten).

Algorithmus

Die Idee der Sweeping-Linie ist, dass alle Punkte in eine Richtung sortiert und dann nacheinander verarbeitet werden.

1. Sortieren Sie alle Punkte entlang einer geraden Linie (der Einfachheit halber nach Koordinaten) $$$x$ )
2. Wir konstruieren ein Dreieck auf den ersten 3 Punkten.
   
   Ferner werden wir für jeden nächsten Punkt Schritte ausführen, die die Invariante bewahren, dass es eine Delaunay-Triangulation für bereits hinzugefügte Punkte und dementsprechend ein MBO für sie gibt.
3. Fügen Sie die Dreiecke hinzu, die aus den sichtbaren Kanten und dem Punkt selbst bestehen (dh fügen Sie die Kanten des betreffenden Punkts zu allen Enden der sichtbaren Kanten hinzu).
4. Wir überprüfen im Delaunay-Zustand alle Vierecke, die durch die sichtbaren Kanten erzeugt werden. Wenn die Bedingung irgendwo nicht erfüllt ist, bauen wir die Triangulation im Viereck neu auf (ich erinnere mich, dass es nur zwei davon gibt) und führen rekursiv die Prüfung für die Vierecke durch, die durch die Kanten des aktuellen Vierecks erzeugt werden (da erst danach die Delaunay-Bedingung verletzt werden könnte).

Hinweis : In Schritt (4) können Sie während eines rekursiven Starts die Vierecke nicht überprüfen, die durch die Kanten erzeugt werden, die von dem bei dieser Iteration berücksichtigten Punkt stammen (es gibt immer zwei von vier). Meistens sind sie nicht konvex, für konvex ist der Beweis rein geometrisch, ich überlasse es dem Leser. Ferner nehmen wir an, dass nur 2 rekursive Starts für jede Neuerstellung durchgeführt werden.

Überprüfen einer Verzögerungsbedingung

Möglichkeiten, Vierecke auf die Delaunay-Bedingung zu testen, finden Sie im selben Buch [1]. Ich stelle nur fest, dass bei der Auswahl einer Methode mit trigonometrischen Funktionen von dort mit ungenauer Implementierung negative Werte von Sinus erhalten werden können, es sinnvoll ist, sie modulo zu nehmen.

Suche nach sichtbaren Kanten

Es bleibt zu verstehen, wie sichtbare Kanten effektiv gefunden werden können. Beachten Sie, dass sich der zuvor hinzugefügte Punkt S bei der aktuellen Iteration im MBO befindet, da er die größte Koordinate hat $$$x$ und ist auch für den aktuellen Punkt sichtbar. Wenn wir dann feststellen, dass die Enden der sichtbaren Kanten eine durchgehende Kette sichtbarer Punkte bilden, können wir vom Punkt S in beide Richtungen entlang des MBO gehen und die Kanten sammeln, während sie sichtbar sind (die Sichtbarkeit der Kante wird mit dem Vektorprodukt überprüft). Daher ist es zweckmäßig, das MBO als doppelt verbundene Liste zu speichern, wobei bei jeder Iteration sichtbare Kanten entfernt und zwei neue vom betrachteten Punkt hinzugefügt werden.

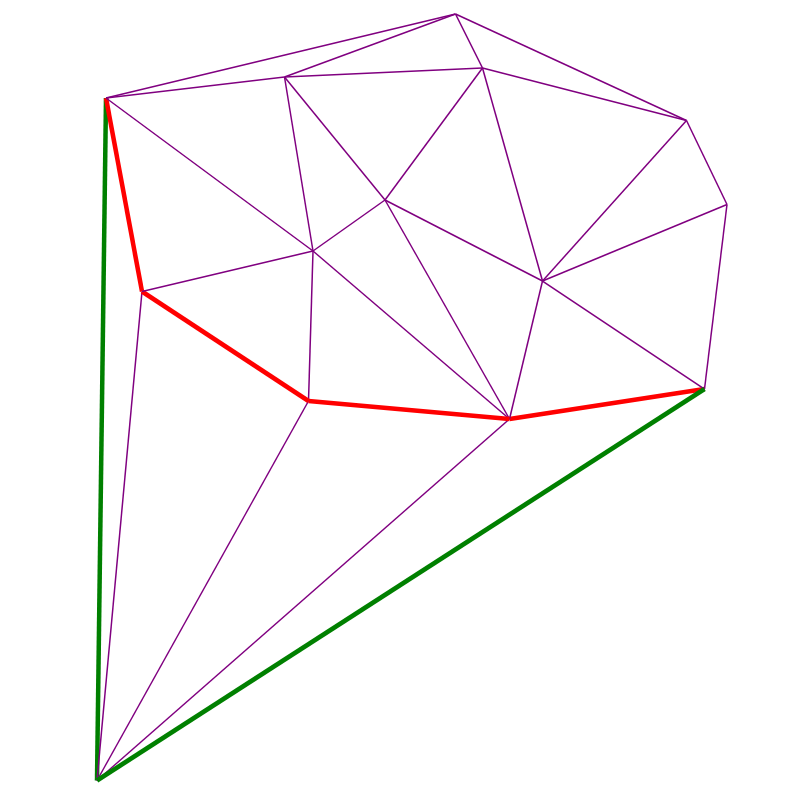
Algorithmusvisualisierung

Zwei rote Punkte - hinzugefügt und vorher. Rote Ränder bilden zu jedem Zeitpunkt den Rekursionsstapel aus Schritt (4):

Algorithmuskorrektheit

Um die Richtigkeit des Algorithmus zu beweisen, reicht es aus, die Erhaltung der Invariante in den Schritten (3) und (4) zu beweisen.

Schritt (3)

Nach Schritt (3) erhalten wir offensichtlich eine Triangulation des aktuellen Satzes von Punkten.

Schritt (4)

In dem Prozess von Schritt (4) befinden sich alle Vierecke, die die Delaunay-Bedingung nicht erfüllen (folgt aus der Beschreibung), was bedeutet, dass am Ende von Schritt (4) alle Vierecke die Delaunay-Bedingung erfüllen, dh die Delaunay-Triangulation wird tatsächlich konstruiert. Dann bleibt zu beweisen, dass der Prozess in Schritt (4) eines Tages enden wird. Dies folgt aus der Tatsache, dass alle Kanten, die während der Neuerstellung hinzugefügt werden, vom aktuellen fraglichen Scheitelpunkt stammen (d. H. Schrittweise) $$$k$ es gibt nicht mehr als $$$k-1$ ) und aufgrund der Tatsache, dass wir nach dem Hinzufügen dieser Kanten die von ihnen erzeugten Vierecke nicht berücksichtigen (siehe vorherige Bemerkung), was bedeutet, dass wir nicht mehr als einmal hinzufügen werden.

Zeitliche Komplexität

Im Durchschnitt funktioniert der Algorithmus bei gleichmäßigen Normalverteilungen ziemlich gut (die Ergebnisse sind in der folgenden Tabelle aufgeführt). Es wird davon ausgegangen, dass die Arbeitszeit beträgt $$$O (NlogN)$ . Im schlimmsten Fall findet eine Bewertung statt $$$O (N ^ 2)$ .

Werfen wir einen Blick auf die Arbeitszeit in Teilen und verstehen, welche die größte Auswirkung auf die Gesamtzeit hat:

Nach Richtung sortieren

Für die Sortierung verwenden wir die Schätzung $$$O (NlogN)$ .

Suche nach sichtbaren Kanten

Zunächst zeigen wir, dass die Gesamtzeit für die Suche nach sichtbaren Kanten insgesamt beträgt $$$O (N)$ . Beachten Sie, dass wir bei jeder Iteration alle sichtbaren Kanten und 2 weitere (zuerst nicht sichtbar) in linearer Zeit finden. In Schritt (3) fügen wir dem MBO neue 2 Kanten hinzu. Insgesamt also nicht mehr als $$$2N$ Rippen und verschiedene sichtbare Rippen werden daher nicht mehr sein $$$2N$ . Wir werden auch finden $$$2N$ Kanten, die nicht sichtbar sind. Insgesamt gibt es also keine mehr $$$4N$ Rippen, die der Zeit entsprechen $$$O (N)$ .

Neue Dreiecke bauen

Die Gesamtzeit für die Konstruktion von Dreiecken aus Schritt (3) mit bereits gefundenen sichtbaren Kanten ist offensichtlich $$$O (N)$ .

Triangulation wieder aufbauen

Es bleibt Schritt (4) zu behandeln. Beachten Sie zunächst, dass das Überprüfen der Delaunay-Bedingung und das Wiederherstellen, wenn sie nicht erfüllt sind, recht teure Aktionen sind (obwohl sie funktionieren $$$O (1)$ ) Nur bei Überprüfung der Delaunay-Bedingung können etwa 28 Rechenoperationen ausgeführt werden. Schauen wir uns die durchschnittliche Anzahl der Neuerstellungen in diesem Schritt an. Praktische Ergebnisse für einige Distributionen sind unten angegeben. Für sie möchte ich wirklich sagen, dass die durchschnittliche Anzahl von Umlagerungen mit einer logarithmischen Geschwindigkeit wächst, aber lassen wir dies als Annahme.

Hier möchte ich auch darauf hinweisen, dass die durchschnittliche Anzahl von Umlagerungen pro Punkt stark von der Richtung abweichen kann, in der die Sortierung durchgeführt wird. Für eine Million, die gleichmäßig auf einem langen, niedrigen Rechteck mit einem Seitenverhältnis von 100000: 1 verteilt ist, variiert diese Zahl zwischen 1,2 und 24 (diese Werte werden beim horizontalen bzw. vertikalen Sortieren von Daten erreicht). Daher sehe ich den Punkt darin, die Sortierrichtung auf beliebige Weise auszuwählen (in diesem Beispiel wurden bei willkürlicher Auswahl durchschnittlich etwa 2 Neuerstellungen erhalten) oder manuell auszuwählen, wenn die Daten im Voraus bekannt sind.

Daher dauert die Hauptzeit, die das Programm normalerweise benötigt, Schritt (4). Wenn es schnell läuft, ist es sinnvoll, über eine schnellere Sortierung nachzudenken.

Schlimmster Fall

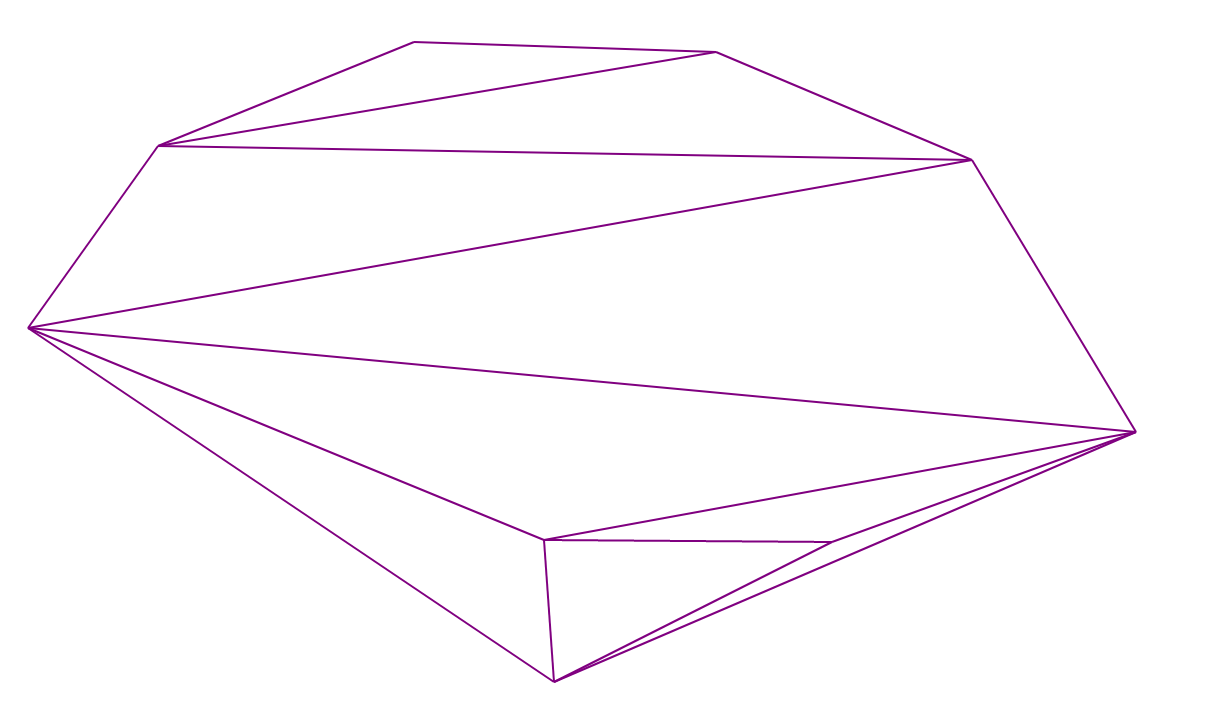
Schlimmster Fall auf $$$k$ Die Iteration erfolgt $$$k-1$ der rekursive Aufruf in Schritt (4), d. h. Summieren über alles i, erhalten wir im schlimmsten Fall das asymptotische Verhalten $$$O (N ^ 2)$ . Das folgende Bild zeigt ein schönes Beispiel, an dem das Programm lange arbeiten kann (durchschnittlich 1100 Neuerstellungen, wenn ein neuer Punkt mit einer Eingabe von 10.000 Punkten hinzugefügt wird).

Vergleich mit einem iterativen Algorithmus zur Konstruktion einer Delaunay-Triangulation unter Verwendung eines kD-Baums

Beschreibung des iterativen Algorithmus

Ich werde den obigen Algorithmus kurz beschreiben. Wenn der nächste Punkt eintrifft, verwenden wir den kD-Baum (ich rate Ihnen, irgendwo darüber zu lesen, wenn Sie es nicht wissen). Wir finden ein Dreieck, das bereits ziemlich nahe daran liegt. Dann umgehen wir die Tiefe und suchen nach einem Dreieck, in das der Punkt selbst fällt. Wir erweitern die Kanten bis zu den Eckpunkten des gefundenen Dreiecks und führen tatsächlich Schritt (4) aus unserem Algorithmus für die neuen Vierecke aus. Da der Punkt außerhalb der Triangulation liegen kann, wird zur Vereinfachung vorgeschlagen, alle Punkte mit einem großen Dreieck abzudecken (um ihn im Voraus zu konstruieren), um das Problem zu lösen.

Ähnlichkeit von Algorithmen

Wenn Punkte in der nach Richtung sortierten Reihenfolge hinzugefügt werden, funktioniert unser Algorithmus tatsächlich genauso wie iterativ, außer dass die Anzahl der Umordnungen geringer ist. Die folgende Animation zeigt dies perfekt. Darauf wurden Punkte von rechts nach links hinzugefügt, und alle sind von einem großen Dreieck bedeckt, das anschließend entfernt wird.

Algorithmusunterschiede

In einem iterativen Algorithmus erfolgt die Lokalisierung eines Punktes (Suche nach dem gewünschten Dreieck) im Durchschnitt über $$$O (logN)$ Bei den obigen Verteilungen treten durchschnittlich 3 Umlagerungen (wie in [1] gezeigt) unter der Bedingung einer willkürlichen Reihenfolge der Punkteversorgung auf. Somit gewinnt die Sweeping-Linie die Zeit des iterativen Algorithmus bei der Lokalisierung, verliert sie jedoch beim Wiederaufbau (was, wie ich mich erinnere, ziemlich schwierig ist). Darüber hinaus arbeitet der iterative Algorithmus online, was auch sein Unterscheidungsmerkmal ist.

Fazit

Hier zeige ich nur einige interessante Triangulationen, die sich aus der Funktionsweise des Algorithmus ergeben.

Schönes Muster

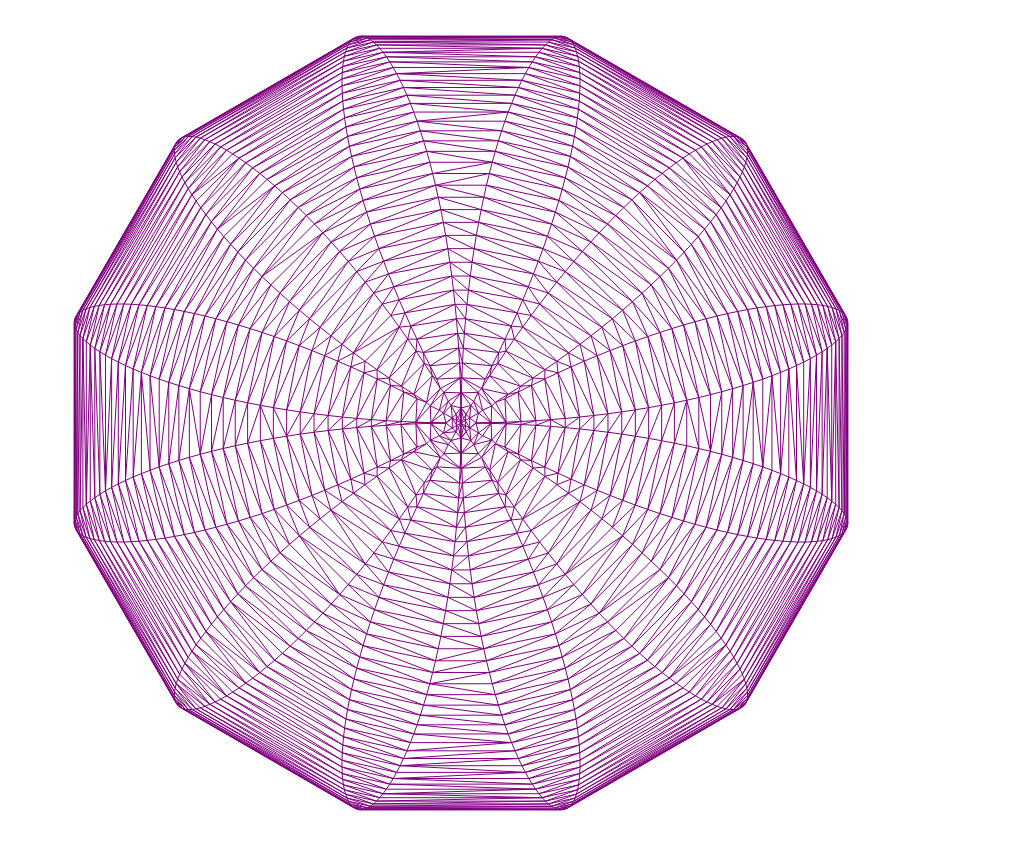
Normalverteilung 1000 Punkte

Gleichmäßige Verteilung, 1000 Punkte

Triangulation an den Standorten aller Städte Russlands

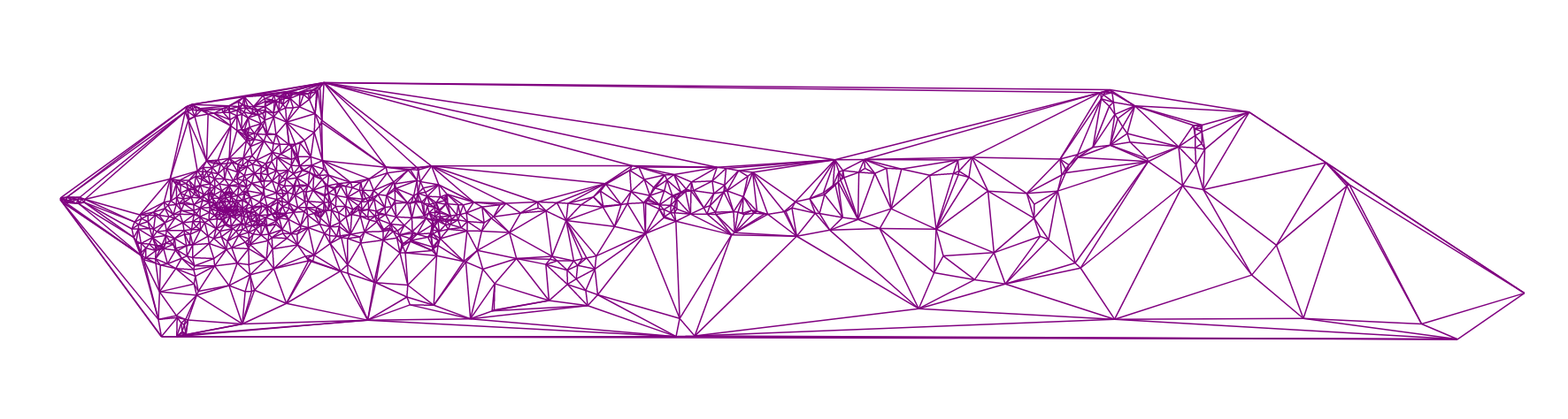
Hier sehen Sie ein Beispiel meines Codes für diesen Algorithmus:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Vielen Dank für Ihre Aufmerksamkeit!

Literatur

[1] Skvortsov A.V. Delaunay-Triangulation und ihre Anwendung. - Tomsk: Verlag Tom. Universität, 2002 .-- 128 p. ISBN 5-7511-1501-5