Labyrinthe: Klassifizierung, Erzeugung, Suche nach Lösungen

Dieser klassische Beitrag beschreibt die beliebtesten Methoden zum Erstellen und Durchlaufen von Labyrinthen. Der Artikel ist in vier Teile gegliedert: Klassifizierung, Generierungsalgorithmen, Algorithmen zum Lösen von Labyrinthen und andere Operationen mit Labyrinthen.

Labyrinthklassifikation

Die Labyrinthe als Ganzes (und damit die Algorithmen zu ihrer Erstellung) können in sieben verschiedene Klassifikationen unterteilt werden: Dimension, Hyperdimension, Topologie, Tessellation, Routing, Textur und Priorität. Das Labyrinth kann ein Element aus jeder Klasse in einer beliebigen Kombination verwenden.
Dimension: Die Dimensionsklasse bestimmt im Wesentlichen, wie viele Dimensionen im Raum das Labyrinth ausfüllt. Folgende Typen stehen zur Verfügung:

• 
  
  Zweidimensional : Die meisten Labyrinthe, sowohl Papier als auch Real, haben diese Dimension. Das heißt, wir können den Plan des Labyrinths immer auf einem Blatt Papier anzeigen und uns entlang bewegen, ohne andere Korridore des Labyrinths zu überqueren.
• Dreidimensional : Das dreidimensionale Labyrinth hat mehrere Ebenen. darin (zumindest in der orthogonalen Version) können Passagen zusätzlich zu den vier Himmelsrichtungen nach unten und nach oben gehen. Ein 3D-Labyrinth wird häufig als eine Reihe von 2D-Ebenen mit Treppen nach oben und unten dargestellt.
• 
  
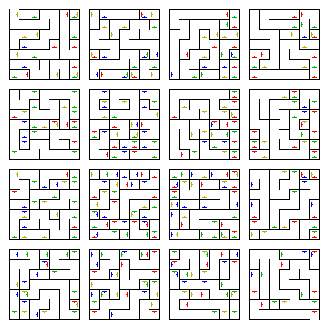
  Höhere Dimensionen : Sie können vierdimensionale und noch mehrdimensionale Labyrinthe erstellen. Manchmal werden sie als 3D-Labyrinthe mit „Portalen“ dargestellt, die durch die vierte Dimension führen, z. B. Portale in die „Vergangenheit“ und „Zukunft“.
• 
  
  Verflechtung : Labyrinthe mit Verflechtung - dies sind im Wesentlichen zweidimensionale (oder eher 2,5-dimensionale) Labyrinthe, in denen sich jedoch Passagen überlappen können. Bei der Anzeige ist es normalerweise ziemlich offensichtlich, wo sich die Sackgassen befinden und wie sich ein Durchgang über dem anderen befindet. Labyrinthe aus der realen Welt, in denen Brücken einen Teil des Labyrinths mit einem anderen verbinden, sind teilweise miteinander verflochten.

Hyperdimension: Die Klassifizierung nach Hyperdimension entspricht der Dimension eines Objekts, das sich durch ein Labyrinth bewegt, und nicht dem Labyrinth selbst. Folgende Typen stehen zur Verfügung:

• 
  
  Nicht-Hyperlabyrinthe : Fast alle Labyrinthe, auch solche, die in hoher Dimensionalität oder mit speziellen Regeln erstellt wurden, sind normalerweise Nicht-Hyperlabyrinthe. In ihnen arbeiten wir mit einem Punkt oder einem kleinen Objekt, zum Beispiel einem Ball oder dem Spieler selbst, der sich von Punkt zu Punkt bewegt, und die asphaltierte Route bildet eine Linie. An jedem Punkt gibt es eine leicht zählbare Anzahl von Auswahlmöglichkeiten.
• Hyperlabyrinthe: Hyperlabyrinthe sind Labyrinthe, in denen das zu lösende Objekt nicht nur ein Punkt ist. Ein Standardhyperlabyrinth (oder Hyperlabyrinth erster Ordnung) besteht aus einer Linie, die eine Oberfläche bildet, wenn sie sich entlang eines Pfades bewegt. Hyperlabyrinth kann nur in 3D oder in einem Medium mit einer größeren Dimension existieren, und der Eingang zum Hyperlabyrinth ist oft kein Punkt, sondern eine Linie. Hyperlabyrinth ist grundlegend anders, weil es notwendig ist, mehrere Teile entlang der Linie zu berücksichtigen und gleichzeitig mit ihnen zu arbeiten, und zu jedem Zeitpunkt gibt es eine nahezu unendliche Anzahl von Zuständen und Optionen für das, was mit der Linie getan werden kann. Die Lösungslinie ist unendlich oder ihre Endpunkte liegen außerhalb des Hyperlabyrinths, um zu vermeiden, dass die Linie zu einem Punkt komprimiert wird, da sie in diesem Fall als Nicht-Hyperlabyrinth betrachtet werden kann.
• Hyperhyperlabyrinth: Hyperlabyrinthe können beliebig hoch dimensioniert sein. Hyperhyperlabyrinth (oder Hyperlabyrinth zweiter Ordnung) erhöht erneut die Dimension des zu lösenden Objekts. Hier ist das zu lösende Objekt eine Ebene, die, wenn sie sich entlang des Pfades bewegt, eine dreidimensionale Figur bildet. Hyperhyperlabyrinth kann nur in einer 4D- oder höherdimensionalen Umgebung existieren.

Topologie: Die Topologieklasse beschreibt die Geometrie des Labyrinthraums, in dem er als Ganzes existiert. Folgende Typen stehen zur Verfügung:

• 
  
  Normal : Dies ist das Standardlabyrinth im euklidischen Raum.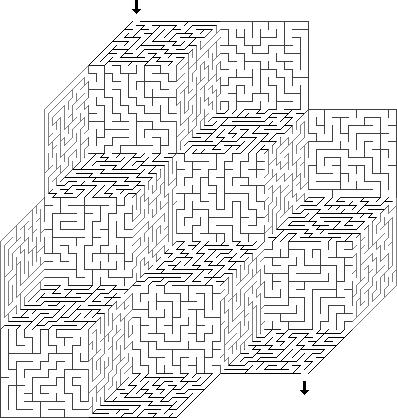
• 
  
  Planair : Der Begriff „Planair“ beschreibt jedes Labyrinth mit einer ungewöhnlichen Topologie. In der Regel bedeutet dies, dass die Ränder des Labyrinths auf interessante Weise miteinander verbunden sind. Beispiele: Labyrinthe auf der Oberfläche eines Würfels, Labyrinthe auf der Oberfläche eines Mobius-Streifens und Labyrinthe, die denen eines Torus entsprechen, bei dem die linke und rechte, obere und untere Seite paarweise verbunden sind.

Tessellation: Eine Klassifizierung der Geometrie der einzelnen Zellen, aus denen das Labyrinth besteht. Bestehende Typen:

• 
  
  Orthogonal : Dies ist ein rechteckiges Standardgitter, in dem Zellen Passagen haben, die sich im rechten Winkel schneiden. Im Rahmen der Tessellation können sie auch als Gammalabyrinthe bezeichnet werden.
• 
  
  Delta : Delta-Labyrinthe bestehen aus verbundenen Dreiecken, und an jede Zelle können bis zu drei Passagen angeschlossen werden.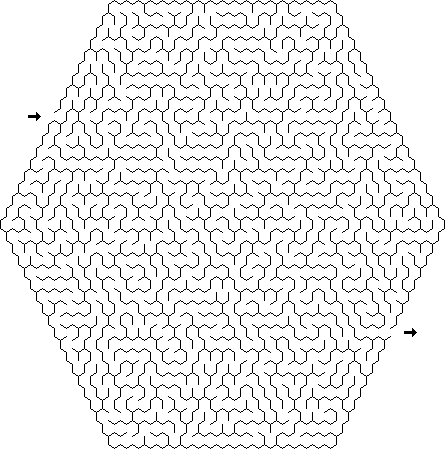
• 
  
  Sigma : Sigma-Labyrinthe bestehen aus verbundenen Sechsecken. Jede Zelle kann bis zu sechs Durchgänge haben.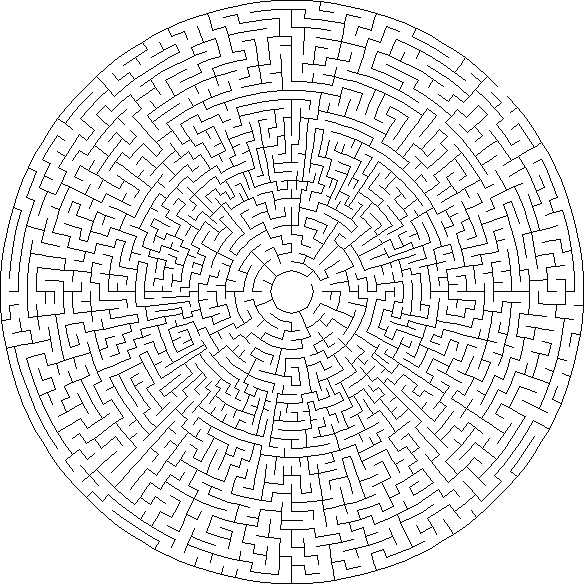
• 
  
  Theta : Theta-Labyrinthe bestehen aus konzentrischen Kreisen von Durchgängen, bei denen der Anfang oder das Ende in der Mitte und der andere am äußeren Rand liegt. Zellen haben normalerweise vier mögliche Verbindungspfade, aber aufgrund der größeren Anzahl von Zellen in den äußeren Ringen der Durchgänge kann es mehr geben.
• 
  
  Epsilon : Epsilon-Labyrinthe bestehen aus verbundenen Achtecken oder Quadraten. Jede Zelle in ihnen kann bis zu acht oder vier Durchgänge haben.
• 
  
  Zeta : Das Zeta-Labyrinth befindet sich in einem rechteckigen Raster. Nur neben horizontalen und vertikalen Passagen sind diagonale Passagen in einem Winkel von 45 Grad zulässig.
• 
  
  Omega : Der Begriff Omega bezieht sich auf fast jedes Labyrinth mit konstanter nicht orthogonaler Tessellation. Delta, Sigma, Theta und Ipsilon Labyrinthe sind von diesem Typ, wie viele andere Schemata, die Sie sich vorstellen können, zum Beispiel ein Labyrinth, das aus Paaren rechtwinkliger Dreiecke besteht.
• 
  
  Riss : Ein Risslabyrinth ist ein amorphes Labyrinth ohne ständige Tessellation, in dem sich Wände und Gehwege in zufälligen Winkeln befinden.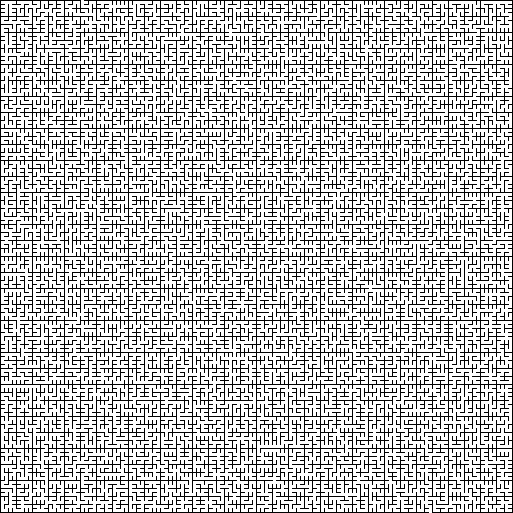
• 
  
  Fraktal : Ein fraktales Labyrinth ist ein Labyrinth aus kleineren Labyrinthen. Ein fraktales Labyrinth aus verschachtelten Zellen ist ein Labyrinth in jeder Zelle, in dem andere Labyrinthe platziert sind, und dieser Vorgang kann mehrmals wiederholt werden. Ein unendlich rekursives fraktales Labyrinth ist ein echtes Fraktal, in dem sich der Inhalt des Labyrinths selbst repliziert und ein im Wesentlichen unendlich großes Labyrinth erzeugt.

Routing: Die Klassifizierung nach Routing ist wahrscheinlich der interessanteste Aspekt bei der Erzeugung von Labyrinthen. From ist Arten von Durchgängen innerhalb der Geometrie zugeordnet, die in den oben beschriebenen Kategorien definiert sind.

• 
  
  Ideal : „Ideal“ ist ein Labyrinth ohne Schleifen oder geschlossene Kreisläufe und ohne unerreichbare Bereiche. Es wird auch ein einfach verbundenes Labyrinth genannt. Von jedem Punkt gibt es genau einen Pfad zu einem anderen Punkt. Labyrinth hat nur eine Lösung. Aus programmtechnischer Sicht kann ein solches Labyrinth als Baum, als Verbindungsmenge von Zellen oder Eckpunkten beschrieben werden.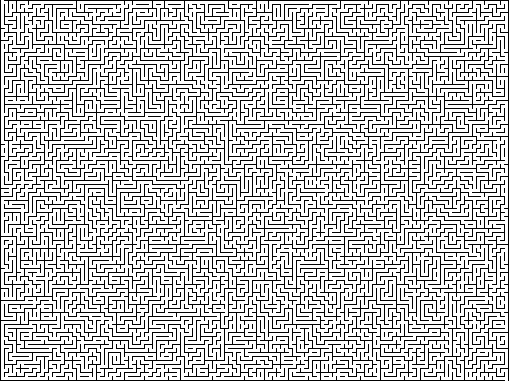
• 
  
  Geflochten : Geflochten bedeutet, dass es im Labyrinth keine Sackgassen gibt. Es wird auch das rein mehrfach verbundene Labyrinthlabyrinth genannt. In einem solchen Labyrinth werden Passagen verwendet, die geschlossen sind und zueinander zurückkehren (daher der Name „Korbweide“). Dadurch verbringen sie mehr Zeit damit, im Kreis zu laufen, anstatt in Sackgassen zu geraten. Ein hochwertiges gewebtes Labyrinth kann viel komplizierter sein als ein ideales Labyrinth derselben Größe.
• 
  
  Single-Route (Unicursal) : Single- Route bedeutet ein Labyrinth ohne Gabeln. Das Einweg-Labyrinth enthält einen langen, gewundenen Durchgang, der die Richtung im gesamten Labyrinth ändert. Es ist nicht sehr kompliziert, nur wenn Sie nicht versehentlich auf halber Strecke zurückkehren und nicht zum Anfang zurückkehren.
• 
  
  Spärlich: Ein spärliches Labyrinth durchläuft nicht jede Zelle, dh einige von ihnen werden nicht erstellt. Dies impliziert das Vorhandensein nicht erreichbarer Bereiche, dh in gewissem Sinne ist es das Gegenteil des Weidenlabyrinths. Ein ähnliches Konzept kann beim Hinzufügen von Wänden angewendet werden, sodass Sie ein unebenes Labyrinth mit breiten Gängen und Räumen erhalten.
• Teilweise Wicker: Teilweise Wicker Maze ist ein gemischtes Labyrinth, das sowohl Schleifen als auch Sackgassen aufweist. Das Wort „Korbweide“ kann zur quantitativen Beurteilung verwendet werden, dh ein „Labyrinth mit starkem Weben“ ist ein Labyrinth mit vielen entfernten Schleifen oder Wänden, und es gibt nur wenige im „Labyrinth mit schwachem Weben“.

Textur: Die Texturklassifizierung beschreibt den Stil von Durchläufen mit unterschiedlichem Routing und unterschiedlicher Geometrie. Textur ist nicht nur ein Parameter, der ein- oder ausgeschaltet werden kann. Hier einige Beispiele für Variablen:

• 
  
  Bias : In einem Labyrinth mit verschobenen Passagen tendieren gerade Passagen eher in eine Richtung als in andere. In einem Labyrinth mit hoher horizontaler Verschiebung haben wir beispielsweise lange Passagen von links nach rechts und nur kurze Passagen von oben nach unten, die sie verbinden. Ein solches Labyrinth ist normalerweise schwieriger „über die Fasern“ zu führen.
• 
  
  Überflug : Die Überflugmetrik bestimmt, wie lange es dauert, bis erzwungene Abbiegungen auftreten. In einem Labyrinth mit geringer Spannweite gibt es keine geraden Passagen, die länger als drei oder vier Zellen sind, und es sieht sehr zufällig aus. In einem Labyrinth mit einer hohen Spannweite hat das Labyrinth einen großen Prozentsatz an langen Durchgängen, wodurch es wie ein Mikrochip aussieht.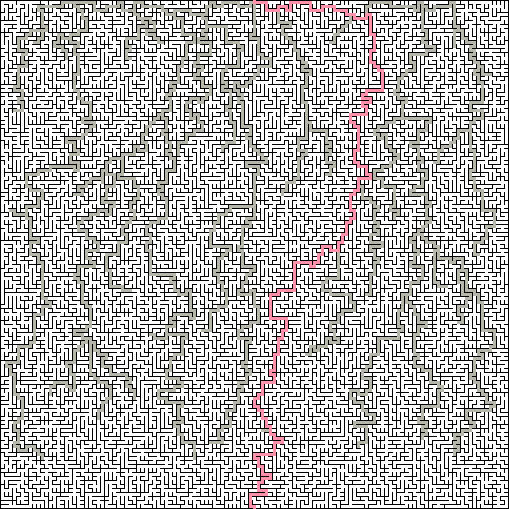
• 
  
  Elitismus: Der Indikator „ Elitismus “ des Labyrinths bestimmt die Länge der Lösung im Verhältnis zur Größe des Labyrinths. Elite-Labyrinthe haben normalerweise eine kurze, direkte Lösung, während in Nicht-Elite-Labyrinthen die Lösung einen großen Teil des Labyrinthbereichs durchläuft. Ein hochwertiges Elite-Labyrinth kann viel komplizierter sein als ein Nicht-Elite-Labyrinth.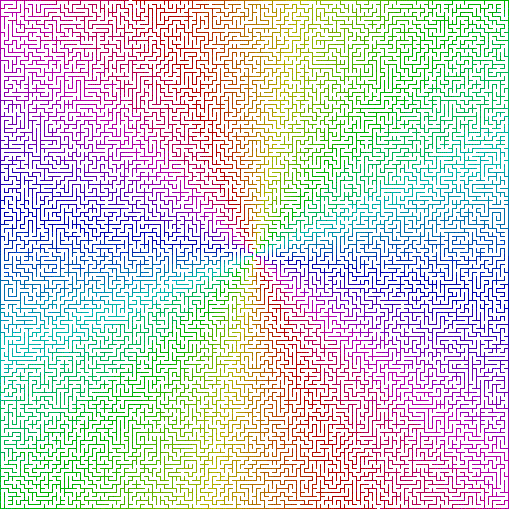
• 
  
  Symmetrie : Ein symmetrisches Labyrinth hat symmetrische Passagen, beispielsweise in der Rotationssymmetrie relativ zur Mitte oder entlang der horizontalen oder vertikalen Achse. Das Labyrinth kann teilweise oder vollständig symmetrisch sein und das Muster beliebig oft wiederholen.
• 
  
  Homogenität: Ein homogener Algorithmus erzeugt alle möglichen Labyrinthe mit gleicher Wahrscheinlichkeit. Ein Labyrinth kann als homogen bezeichnet werden, wenn es wie ein typisches Labyrinth aussieht, das durch einen homogenen Algorithmus erzeugt wird. Ein heterogener Algorithmus kann theoretisch auch alle möglichen Labyrinthe in jedem Raum erzeugen, jedoch nicht mit gleicher Wahrscheinlichkeit. Die Heterogenität kann noch weiter gehen - es kann Labyrinthe geben, die der Algorithmus niemals erzeugen wird.
• Flussfluss: Die Eigenschaft „Fluss“ bedeutet, dass der Algorithmus beim Erstellen eines Labyrinths nach den benachbarten Zellen (oder Wänden) sucht und diese reinigt, dh sie fließt (daher der Begriff „Fluidität“) wie Wasser in die noch nicht erstellten Teile des Labyrinths. In einem idealen Labyrinth mit einer geringeren Durchflussrate gibt es normalerweise viele kurze Sackgassen, und in einem „flüssigeren“ Labyrinth gibt es weniger Sackgassen, aber sie sind länger.

Priorität: Diese Klassifizierung zeigt, dass die Prozesse zur Erstellung von Labyrinthen in zwei Haupttypen unterteilt werden können: Hinzufügen von Wänden und Schnitzen von Passagen. Wenn es darum geht, dies zu generieren, kommt es normalerweise nur auf den Unterschied in den Algorithmen und nicht auf merkliche Unterschiede in den Labyrinthen an, aber es ist immer noch nützlich, dies zu berücksichtigen. Das gleiche Labyrinth wird oft auf beide Arten erzeugt:

• Hinzufügen von Wänden: Algorithmen, für die Wände Priorität haben, beginnen mit einem leeren Bereich (oder einem Außenrand) und fügen dabei Wände hinzu. In der realen Welt fügen echte Labyrinthe, die aus Hecken, Decken oder Holzwänden bestehen, definitiv Wände hinzu.
• Gänge schneiden: Algorithmen, deren Priorität Gänge sind, beginnen mit einem festen Block und schneiden dabei Passagen. In der realen Welt sind solche Labyrinthe Minentunnel oder Labyrinthe in Rohren.
• 
  
  Vorlage: Natürlich können Labyrinthe gleichzeitig Passagen schneiden und Wände hinzufügen. Einige Computeralgorithmen machen das. Eine Labyrinthvorlage ist ein Grafikbild, das kein Labyrinth ist, das sich in der geringsten Anzahl von Schritten in ein echtes Labyrinth verwandelt, aber dennoch die Textur der ursprünglichen Grafikvorlage beibehält. Komplexe Labyrinthstile wie sich überschneidende Spiralen lassen sich leichter als Muster in einem Computer implementieren, als zu versuchen, das richtige Labyrinth zu erstellen und dabei seinen Stil beizubehalten.

Sonstiges: Das Obige ist keineswegs eine vollständige Liste aller möglichen Klassen oder Elemente innerhalb jeder Klasse. Dies sind nur die Arten von Labyrinthen, die ich selbst geschaffen habe. Beachten Sie, dass fast jede Art von Labyrinth, einschließlich Labyrinthen mit speziellen Regeln, als gerichteter Graph ausgedrückt werden kann, in dem es in jedem Zustand eine endliche Anzahl von Zuständen und eine endliche Anzahl von Auswahlmöglichkeiten gibt. Dies wird als Äquivalenz der Labyrinthe bezeichnet . Hier sind einige andere Klassifikationen und Arten von Labyrinthen:

• 
  
  Orientierung : An bestimmten Stellen können Sie sich nur in eine Richtung bewegen. Aus programmtechnischer Sicht wird ein solches Labyrinth durch einen gerichteten Graphen beschrieben, im Gegensatz zu einem ungerichteten Graphen, der alle anderen Typen beschreibt.
• 
  
  Segmentierung : Das Labyrinth kann verschiedene Teile haben, die verschiedenen Klassen entsprechen.
• 
  
  Labyrinthe von unendlicher Länge: Wir können ein unendlich langes Labyrinth erstellen (eine endliche Anzahl von Spalten und eine beliebige Anzahl von Zeilen), aber gleichzeitig nur einen Teil des Labyrinths im Speicher speichern, von einem Ende zum anderen „scrollen“ und beim Erstellen der nächsten die vorherigen Zeilen zerstören. Ein Beispiel ist eine modifizierte Version des Hunt and Kill-Algorithmus. Man kann sich ein möglicherweise endloses Labyrinth in Form eines langen Films vorstellen, der aus einzelnen Bildern besteht. Es werden jeweils nur zwei aufeinanderfolgende Frames gespeichert. Lassen Sie uns den Hunt and Kill-Algorithmus ausführen, obwohl er eine Verzerrung erzeugt, die für den oberen Frame anfällig ist, sodass er zuerst endet. Nach der Fertigstellung wird der Rahmen nicht mehr benötigt, Sie können ihn drucken oder etwas anderes damit machen. Wie auch immer, verwerfen Sie es, machen Sie den teilweise erstellten unteren Rahmen zu einem neuen oberen Rahmen und löschen Sie den neuen unteren Rahmen. Wiederholen Sie den Vorgang, bis wir aufhören möchten, und warten Sie dann, bis Hunt And Kill beide Frames abgeschlossen hat. Die einzige Einschränkung besteht darin, dass das Labyrinth niemals einen Pfad hat, der sich über eine Länge von mehr als zwei Frames zum Eingang hin verzweigt. Der einfachste Weg, ein endloses Labyrinth zu erstellen, ist der Eller-Algorithmus oder der Sidewinder-Algorithmus, da sie bereits zeilenweise Labyrinthe erstellen, sodass Sie sie einfach endlos Linien zum Labyrinth hinzufügen lassen können.
• 
  
  Virtuelle fraktale Labyrinthe: Virtuell ist ein Labyrinth, in dem nicht das gesamte Labyrinth gleichzeitig gespeichert wird. Beispielsweise kann nur ein Teil der 100 x 100 Durchgänge in der Nähe Ihres Standorts in einer Simulation gespeichert werden, in der Sie durch ein großes Labyrinth gehen. Die Erweiterung verschachtelter fraktaler Labyrinthe kann verwendet werden, um riesige virtuelle Labyrinthe zu erstellen, beispielsweise eine Milliarde pro Milliarde Durchgänge. Wenn wir eine echte Kopie des Labyrinths von einer Milliarde pro Milliarde Pässen (mit einem Abstand von sechs Fuß zwischen den Passagen) bauen würden, würde es die Erdoberfläche mehr als 6.000 Mal füllen! Stellen Sie sich ein Labyrinth von 10 ⁹ bis 10 ⁹ Durchgängen oder ein geschlossenes Labyrinth mit nur 9 Ebenen vor. Wenn wir mindestens ein 100x100-Teil um uns haben möchten, reicht es aus, auf der untersten Ebene ein Unterlabyrinth von 100x100 Durchgängen und sieben 10x10-Labyrinthen zu erstellen, in das es eingebettet ist, um genau zu wissen, wo sich die Wände innerhalb des 100x100-Teils befinden. (Eigentlich ist es besser, vier benachbarte Teile mit einer Größe von 100 x 100 zu haben, die ein Quadrat bilden, falls Sie sich in der Nähe der Kante oder Ecke des Teils befinden. Hier gilt jedoch das gleiche Konzept.) Um sicherzustellen, dass das Labyrinth beim Bewegen konstant und unverändert bleibt, haben wir eine Formel: Definieren einer zufälligen Startnummer für jede Koordinate auf jeder Verschachtelungsebene. Virtuelle fraktale Labyrinthe ähneln dem Mandelbrot-Fraktal, in dessen Bildern es virtuell existiert, und wir müssen eine bestimmte Koordinate mit einer ziemlich hohen Vergrößerung besuchen. so dass es erscheint.

Labyrinth-Algorithmen

Hier ist eine Liste verallgemeinerter Algorithmen zum Erstellen der verschiedenen oben beschriebenen Labyrinthklassen:

• 
  
  Ideal : Um ein ideales Standardlabyrinth zu schaffen, muss es normalerweise „wachsen“, um sicherzustellen, dass keine Schleifen und isolierten Bereiche vorhanden sind. Wir beginnen an der Außenwand und fügen zufällig ein Fragment der Wand hinzu, das sie berührt. Wir fügen dem Labyrinth weiterhin zufällig Wandsegmente hinzu, stellen jedoch sicher, dass jedes neue Segment ein Ende der vorhandenen Wand berührt und sich das andere Ende im noch nicht erstellten Teil des Labyrinths befindet. Wenn Sie ein Wandsegment hinzufügen, dessen beide Enden vom Rest des Labyrinths getrennt sind, wird eine nicht verbundene Wand mit einer Schleife erstellt. Wenn Sie ein Segment hinzufügen, dessen beide Enden das Labyrinth berühren, entsteht ein nicht erreichbarer Bereich. Dies ist eine Methode zum Hinzufügen von Wänden. Es ist fast analog zum Ausschneiden von Passagen, bei denen Teile der Passagen so geschnitten werden, dass nur ein Ende den vorhandenen Pass berührt.
• 
  
  : , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
• 
  
  : — , , , , . U- , , , , . . , : , , , . , . , .
• 
  
  : , . , , . - , , , , .
• 3D : , , , . - .
• 
  
  : , , . ( ): , , , . , . , ; , . , , .
• 
  
  Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
• 
  
  : «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
• 
  
  : — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
• 
  
  Planair : Planair- , . — . , .
• 
  
  : , , , -, , , , . , . , , , , , .

Es gibt viele Möglichkeiten, perfekte Labyrinthe zu erstellen, und jeder von ihnen hat seine eigenen Eigenschaften. Unten finden Sie eine Liste spezifischer Algorithmen. Alle beschreiben die Schaffung eines Labyrinths durch Ausschneiden von Passagen. Sofern nicht anders angegeben, kann jedes auch durch Hinzufügen von Wänden implementiert werden:

• 
  
  Rekursiver Backtracker : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
• 
  
  : , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
• 
  
  Prims Algorithmus (true) : Dieser Algorithmus erstellt einen minimalen Spanning Tree, indem er eindeutig zufällige Kantengewichte verarbeitet. Der erforderliche Speicherplatz ist proportional zur Größe des Labyrinths. Wir beginnen an einem beliebigen Scheitelpunkt (das fertige Labyrinth ist das gleiche, egal von oben, wo wir beginnen). Wir wählen die Kante des Durchgangs mit dem kleinsten Gewicht aus, das das Labyrinth mit einem Punkt verbindet, der sich noch nicht darin befindet, und befestigen es dann am Labyrinth. Das Labyrinth ist fertig, wenn die fraglichen Kanten nicht mehr übrig sind. Um die nächste Kante effizient auszuwählen, benötigen Sie eine Prioritätswarteschlange (normalerweise mithilfe eines Heaps implementiert), in der alle Kanten des Rahmens gespeichert sind. Dieser Algorithmus ist jedoch ziemlich langsam, da die Auswahl von Elementen aus dem Heap log (n) Zeit benötigt. Daher ist es besser, den Kraskal-Algorithmus zu bevorzugen, der auch einen minimalen Spannbaum erzeugt, da er schneller ist und Labyrinthe mit identischer Struktur erzeugt. Tatsächlich können die Algorithmen Prima und Kraskal mit demselben zufälligen Startwert dieselben Labyrinthe erzeugen.
• 
  
  Prims Algorithmus (vereinfacht) : Dieser Prims Algorithmus erstellt einen minimalen Spannbaum. Es wird so vereinfacht, dass alle Kantengewichte gleich sind. Es erfordert eine Speicherkapazität proportional zur Größe des Labyrinths. Wir gehen von einem zufälligen Peak aus. Wir wählen zufällig den Rand des Durchgangs aus, der das Labyrinth mit einem Punkt verbindet, der sich noch nicht darin befindet, und befestigen ihn dann am Labyrinth. Das Labyrinth ist fertig, wenn die fraglichen Kanten nicht mehr übrig sind. Da die Kanten schwerelos und nicht geordnet sind, können sie als einfache Liste gespeichert werden, dh die Auswahl der Elemente aus der Liste erfolgt sehr schnell und nimmt konstante Zeit in Anspruch. Daher ist es viel schneller als der echte Prim-Algorithmus mit zufälligen Kantengewichten. Die erzeugte Labyrinthtextur hat eine geringere Flussrate und eine einfachere Lösung als die echte Prim-Methode, da sie sich wie verschütteter Sirup gleichmäßig vom Startpunkt aus verteilt und keine Rippenfragmente mit höherem Gewicht umgeht, die später berücksichtigt werden.
• 
  
  Prims Algorithmus (modifiziert) : Dieser Prims Algorithmus erstellt einen minimalen Spannbaum, der so modifiziert ist, dass alle Gewichte der Kanten gleich sind. Es ist jedoch so implementiert, dass anstelle von Kanten Zellen betrachtet werden. Die Speichermenge ist proportional zur Größe des Labyrinths. Während des Erstellungsprozesses kann jede Zelle einen von drei Typen haben: (1) „intern“: Die Zelle ist Teil des Labyrinths und bereits darin ausgeschnitten. (2) „Grenze“: Die Zelle ist nicht Teil des Labyrinths und wurde noch nicht ausgeschnitten, befindet sich jedoch neben der Zelle, die bereits „intern“ ist, und (3) „extern“: Die Zelle ist noch nicht Teil des Labyrinths, und keiner ihrer Nachbarn ist auch die „interne“ Zelle. Wir beginnen mit der Auswahl einer Zelle, machen sie "intern" und setzen für alle Nachbarn den Typ auf "Grenze". Wir wählen zufällig die "Grenz" -Zelle aus und schneiden einen Durchgang von einer der benachbarten "internen" Zellen hinein. Wir ändern den Status dieser "Grenzzelle" in "intern" und ändern den Typ aller Nachbarn von "extern" in "Grenze". Das Labyrinth ist abgeschlossen, wenn keine "Grenz" -Zellen mehr vorhanden sind (dh keine "externen" Zellen mehr vorhanden sind, was bedeutet, dass jeder "intern" geworden ist). Dieser Algorithmus erzeugt Labyrinthe mit einem sehr niedrigen Ertragsindex, hat viele kurze Deadlocks und eine ziemlich einfache Lösung. Das resultierende Labyrinth ist dem Ergebnis des vereinfachten Prima-Algorithmus sehr ähnlich, mit einem kleinen Unterschied: Die Hohlräume im Spanning Tree werden nur gefüllt, wenn eine Grenzzelle zufällig ausgewählt wird, im Gegensatz zu der dreifachen Wahrscheinlichkeit, diese Zelle durch eine der dazu führenden Grenzzellen zu füllen. Darüber hinaus ist der Algorithmus sehr schnell und schneller als der vereinfachte Prim-Algorithmus, da die Kantenliste nicht kompiliert und verarbeitet werden muss.
• 
  
  Aldous-Broder- Algorithmus: Interessant an diesem Algorithmus ist, dass er homogen ist, dh mit gleicher Wahrscheinlichkeit alle möglichen Labyrinthe einer bestimmten Größe erzeugt. Darüber hinaus ist kein zusätzlicher Speicher oder Stapel erforderlich. Wir wählen einen Punkt aus und bewegen uns zufällig in eine benachbarte Zelle. Wenn wir in eine ungeschnittene Zelle geraten sind, schneiden Sie den Durchgang aus der vorherigen Zelle in diese aus. Wir bewegen uns weiter zu benachbarten Zellen, bis wir die Passagen zu allen Zellen herausgeschnitten haben. Dieser Algorithmus erzeugt Labyrinthe mit einer geringen Durchflussrate, die nur geringfügig höher ist als der Kraskal-Algorithmus. (Dies bedeutet, dass es für einen bestimmten Austausch mehr Labyrinthe mit einem niedrigen Ertragsindex als mit einem hohen gibt, da das Labyrinth mit einer durchschnittlichen Wahrscheinlichkeit ebenso niedrig ist.) Das Schlechte an diesem Algorithmus ist, dass er sehr langsam ist, weil er keine intellektuelle Suche nach letzterem durchführt Zellen, das heißt in der Tat, haben keine Garantien für die Fertigstellung. Aufgrund seiner Einfachheit kann es jedoch schnell viele Zellen durchlaufen, sodass es schneller abgeschlossen wird, als Sie vielleicht denken. Im Durchschnitt dauert die Fertigstellung siebenmal länger als bei Standardalgorithmen, obwohl es in schlechten Fällen viel länger dauern kann, wenn der Zufallszahlengenerator die letzten Zellen ständig vermeidet. Es kann als Hinzufügen von Wänden implementiert werden, wenn die Grenzwand als einzelner Scheitelpunkt betrachtet wird, d. H. Wenn die Bewegung uns beispielsweise zur Grenzwand bewegt, teleportieren wir uns zu einem zufälligen Punkt entlang der Grenze und bewegen uns erst dann weiter. Beim Hinzufügen von Wänden funktioniert es fast doppelt so schnell, da die Teleportation entlang der Grenzmauer einen schnelleren Zugang zu den entfernten Teilen des Labyrinths ermöglicht.
• 
  
  Wilsons Algorithmus : Dies ist eine verbesserte Version des Aldous-Broder-Algorithmus. Er erzeugt Labyrinthe mit genau der gleichen Textur (die Algorithmen sind homogen, dh alle möglichen Labyrinthe werden mit gleicher Wahrscheinlichkeit erzeugt), aber der Wilson-Algorithmus ist viel schneller. Es braucht Speicher bis zur Größe des Labyrinths. Wir beginnen mit einer zufällig ausgewählten anfänglichen Labyrinthzelle. Wir wählen eine zufällige Zelle aus, die noch nicht Teil des Labyrinths ist, und führen einen zufälligen Spaziergang durch, bis wir eine Zelle finden, die bereits zum Labyrinth gehört. Sobald wir auf den bereits erstellten Teil des Labyrinths stoßen, kehren wir zur ausgewählten zufälligen Zelle zurück und schneiden den gesamten Pfad aus, indem wir diese Zellen zum Labyrinth hinzufügen. Genauer gesagt, wenn wir auf dem Weg zurückkehren, schneiden wir jede Zelle in der Richtung ein, in der der zufällige Spaziergang beim letzten Verlassen der Zelle stattgefunden hat. Dies vermeidet das Auftreten von Schleifen entlang des Rückweges, so dass ein langer Durchgang das Labyrinth verbindet. Das Labyrinth ist abgeschlossen, wenn alle Zellen daran befestigt sind. Der Algorithmus hat die gleichen Geschwindigkeitsprobleme wie Aldous-Broder, da es lange dauern kann, den ersten zufälligen Pfad zur ursprünglichen Zelle zu finden, aber nach dem Platzieren mehrerer Pfade wird der Rest des Labyrinths ziemlich schnell herausgeschnitten. Im Durchschnitt läuft es fünfmal schneller als Aldous-Broder und weniger als zweimal langsamer als die besten Algorithmen. Es ist zu bedenken, dass das Hinzufügen von Wänden doppelt so schnell funktioniert, da die gesamte Grenzmauer anfangs Teil des Labyrinths ist, sodass sich die ersten Wände viel schneller verbinden.
• 
  
  Hunt and Kill- Algorithmus : Dieser Algorithmus ist praktisch, da er keinen zusätzlichen Speicher oder Stapel benötigt und daher zum Erstellen großer Labyrinthe oder Labyrinthe auf schwachen Computern geeignet ist, da nicht genügend Speicherplatz zur Verfügung steht. Da es keine Regeln gibt, die ständig befolgt werden müssen, ist es auch am einfachsten, Labyrinthe mit unterschiedlichen Texturen damit zu ändern und zu erstellen. Es ähnelt fast einem rekursiven Backtracker, nur dass keine Zelle in der Nähe der aktuellen Position erstellt wurde. Wir wechseln in den "Jagd" -Modus und scannen systematisch das Labyrinth, bis wir eine nicht erstellte Zelle neben der bereits geschnittenen Zelle finden. In dieser Phase beginnen wir wieder mit dem Schneiden an diesem neuen Standort. Das Labyrinth ist abgeschlossen, wenn im "Jagd" -Modus alle Zellen gescannt werden. Dieser Algorithmus neigt dazu, Labyrinthe mit einer hohen Flussrate zu erzeugen, die jedoch nicht so hoch sind wie der rekursive Backtracker. Sie können es zwingen, Labyrinthe mit einer niedrigeren Durchflussrate zu erzeugen, die häufiger in den "Jagd" -Modus wechseln. Es läuft langsamer aufgrund der Zeit, die für die Jagd auf die letzten Zellen aufgewendet wurde, aber nicht viel langsamer als der Kraskal-Algorithmus. Es kann nach dem Prinzip des Hinzufügens von Wänden implementiert werden, wenn Sie gelegentlich zufällig teleportieren, um die Probleme zu vermeiden, die einem rekursiven Backtracker inhärent sind.
• 
  
  Wachsender Algorithmus
  Baum (Wachsender Baum-Algorithmus) : Dies ist ein verallgemeinerter Algorithmus, der Labyrinthe mit unterschiedlichen Texturen erstellen kann. Der erforderliche Speicher kann die Größe des Labyrinths erreichen. Jedes Mal, wenn eine Zelle geschnitten wird, fügen wir sie der Liste hinzu. Wählen Sie eine Zelle aus der Liste aus und schneiden Sie den Durchgang zu der nicht erstellten Zelle daneben aus. Wenn sich in der Nähe der aktuellen Zelle keine nicht erstellten Zellen befinden, löschen Sie die aktuelle Zelle aus der Liste. Das Labyrinth ist abgeschlossen, wenn die Liste nichts anderes enthält. Das Interessante am Algorithmus ist, dass Sie abhängig davon, wie Sie eine Zelle aus der Liste auswählen, viele verschiedene Texturen erstellen können. Wenn Sie beispielsweise immer die zuletzt hinzugefügte Zelle auswählen, wird dieser Algorithmus zu einem rekursiven Backtracker. Wenn Sie Zellen immer zufällig auswählen, verhält es sich ähnlich, jedoch nicht identisch mit dem Prim-Algorithmus. Wenn Sie immer die ältesten Zellen auswählen, die der Liste hinzugefügt wurden, erstellen wir ein Labyrinth mit dem niedrigstmöglichen Ertragsindex, der sogar unter dem des Prim-Algorithmus liegt. Wenn Sie normalerweise die allerletzte Zelle auswählen, aber gelegentlich eine zufällige Zelle auswählen, hat das Labyrinth eine hohe Flussrate, aber eine kurze und direkte Lösung. Wenn eine der neuesten Zellen zufällig ausgewählt wird, hat das Labyrinth eine geringe Durchflussrate, aber eine lange und gewundene Lösung.
• 
  
  Wachsender Waldalgorithmus : Dies ist ein allgemeinerer Algorithmus, der Typen basierend auf Bäumen und Mengen kombiniert. Es ist eine Erweiterung des Baumwachstumsalgorithmus, der im Wesentlichen mehrere Instanzen umfasst, die gleichzeitig erweitert werden. Wir beginnen mit allen Zellen, die zufällig in einer Liste von "neu" sortiert sind. Darüber hinaus hat jede Zelle wie zu Beginn des Kruskal-Algorithmus ihren eigenen Satz. Wählen Sie zunächst eine oder mehrere Zellen aus, indem Sie sie aus der Liste "Neu" in die Liste "Aktiv" verschieben. Wählen Sie eine Zelle aus der Liste "aktiv" aus und schneiden Sie die Passage zur nächsten nicht erstellten Zelle aus der Liste "neu" aus. Fügen Sie der Liste "aktiv" eine neue Zelle hinzu und kombinieren Sie die Sätze von zwei Zellen. Wenn versucht wird, in den vorhandenen Teil des Labyrinths zu schneiden, aktivieren Sie ihn, wenn sich die Zellen in verschiedenen Sätzen befinden, und kombinieren Sie die Zellen, wie im Kraskal-Algorithmus. Wenn sich in der Nähe der aktuellen Zelle keine "neuen" Zellen befinden, verschieben Sie die aktuelle Zelle in die Liste der "fertigen". Das Labyrinth ist abgeschlossen, wenn die Liste der "aktiven" leer wird. Am Ende kombinieren wir alle verbleibenden Mengen wie im Kruskal-Algorithmus. In regelmäßigen Abständen können Sie neue Bäume erstellen, indem Sie wie zu Beginn eine oder mehrere Zellen aus der Liste "Neu" in die Liste "Aktiv" verschieben. Durch Steuern der Anzahl der ursprünglichen Bäume und der Anteile der neu erstellten Bäume können Sie viele eindeutige Texturen generieren, die mit den bereits flexiblen Parametern des Baumwachstumsalgorithmus kombiniert werden.
• 
  
  Ellers Algorithmus : Dies ist ein spezieller Algorithmus, da er nicht nur schneller als alle anderen ist, sondern auch keine offensichtlichen Vorurteile oder Mängel aufweist. Darüber hinaus wird der Speicher beim Erstellen am effizientesten genutzt. Es ist nicht einmal erforderlich, dass sich das gesamte Labyrinth im Speicher befindet, sondern es wird ein Volumen verwendet, das proportional zur Größe der Zeile ist. Es erstellt zeilenweise ein Labyrinth. Nachdem die Generierung der Zeichenfolge abgeschlossen ist, berücksichtigt der Algorithmus dies nicht mehr. Jede Zelle in einer Reihe ist in einer Menge enthalten. Zwei Zellen gehören zu derselben Gruppe, wenn sich zwischen ihnen entlang des bereits erstellten Labyrinths ein Pfad befindet. Mit diesen Informationen können Sie Passagen in der aktuellen Zeile ausschneiden, ohne Schleifen oder isolierte Bereiche zu erstellen. Tatsächlich ist es dem Kraskal-Algorithmus ziemlich ähnlich, nur dass es hier zeilenweise gebildet wird, während Kraskal durch das gesamte Labyrinth schaut. Das Erstellen einer Zeile besteht aus zwei Teilen: Verbinden Sie benachbarte Zellen innerhalb der Zeile zufällig, d. H. wir schneiden horizontale Passagen aus und verbinden dann zufällig die Zellen zwischen der aktuellen und der nächsten Reihe, d.h. vertikale Passagen ausschneiden. Beim Schneiden horizontaler Passagen verbinden wir keine Zellen, die sich bereits im selben Satz befinden (da sonst eine Schleife erstellt wird), und beim Schneiden vertikaler Passagen müssen wir eine Zelle verbinden, wenn sie eine Einheitsgröße hat (wenn Sie sie verlassen, wird ein isolierter Bereich erstellt). Wenn wir horizontale Passagen schneiden, verbinden wir Zellen, wenn sie sich im selben Satz befinden (weil jetzt ein Pfad zwischen ihnen besteht), und wenn wir vertikale Passagen schneiden, wenn wir keine Verbindung mit der Zelle herstellen, legen wir sie in einen separaten Satz (weil sie jetzt vom Rest des Labyrinths getrennt sind ) Die Erstellung beginnt mit der Tatsache, dass vor dem Verbinden der Zellen in der ersten Zeile jede Zelle ihren eigenen Satz hat. Die Erstellung ist abgeschlossen, nachdem die Zellen in der letzten Zeile verbunden wurden. Es gibt eine spezielle Regel für die Fertigstellung: Zum Zeitpunkt der Fertigstellung sollte sich jede Zelle im selben Satz befinden, um isolierte Bereiche zu vermeiden. (Die letzte Zeile wird erstellt, indem jedes der Paare benachbarter Zellen kombiniert wird, die sich noch nicht in derselben Gruppe befinden.) Es ist am besten, die Gruppe mithilfe einer zyklisch doppelt verknüpften Liste von Zellen zu implementieren (die nur ein Array sein kann, das Zellen mit Zellenpaaren auf beiden Seiten derselben Gruppe verbindet) Führen Sie das Einfügen, Löschen und Überprüfen des Vorhandenseins benachbarter Zellen in einem Satz für eine konstante Zeit durch. Das Problem bei diesem Algorithmus ist das Ungleichgewicht bei der Verarbeitung der verschiedenen Kanten des Labyrinths. Um Flecken in Texturen zu vermeiden, müssen Sie Verbindungszellen in den richtigen Proportionen verbinden und überspringen.
• 
  
  Rekursive Division: Dieser Algorithmus ähnelt dem rekursiven Backtracking, da beide Stapel verwenden. Nur funktioniert er nicht mit Gängen, sondern mit Wänden. Wir beginnen mit der Erstellung einer zufälligen horizontalen oder vertikalen Wand, die einen zugänglichen Bereich in einer zufälligen Zeile oder Spalte schneidet, und platzieren zufällig leere Räume entlang dieser. Dann wiederholen wir rekursiv den Vorgang für die beiden durch die Trennwand erzeugten Teilregionen. Um optimale Ergebnisse zu erzielen, müssen Sie eine Abweichung bei der Auswahl von horizontal oder vertikal hinzufügen, die auf den Proportionen des Bereichs basiert. Beispielsweise sollte ein Bereich, dessen Breite doppelt so hoch ist wie die Höhe, häufiger durch vertikale Wände geteilt werden. Dies ist der schnellste Algorithmus ohne Richtungsabweichungen und kann oft sogar mit Labyrinthen konkurrieren, die auf Binärbäumen basieren, da mehrere Zellen gleichzeitig erstellt werden, obwohl er einen offensichtlichen Nachteil in Form langer Wände aufweist, die das Innere des Labyrinths schneiden. Dieser Algorithmus ist eine Art eingebetteter fraktaler Labyrinthe, aber anstatt ständig Labyrinthe von Zellen fester Größe mit Labyrinthen gleicher Größe in jeder Zelle zu erstellen, teilt er einen bestimmten Bereich zufällig in ein Labyrinth zufälliger Größe: 1x2 oder 2x1. Rekursive Division kann nicht zum Ausschneiden von Passagen verwendet werden, da dies zur Schaffung einer offensichtlichen Lösung führt, die entweder entlang der Außenkante folgt oder auf andere Weise die Innenseite direkt schneidet.
• 
  
  Labyrinthe basierend auf Binärbäumen : Tatsächlich sind dies die einfachsten und schnellstmöglichen Algorithmen. Die erstellten Labyrinthe weisen jedoch eine Textur mit einer sehr hohen Vorspannung auf. Für jede Zelle schneiden wir einen Durchgang entweder nach oben oder nach links, jedoch niemals in beide Richtungen. In der Version mit zusätzlichen Wänden wird für jeden nach unten oder rechts führenden Scheitelpunkt ein Wandsegment hinzugefügt, jedoch nicht in beide Richtungen. Jede Zelle ist unabhängig von allen anderen Zellen, da wir beim Erstellen nicht den Status einiger anderer Zellen überprüfen müssen. Daher ist dies ein realer Algorithmus zum Erzeugen von Labyrinthen ohne Speicher, der nicht durch die Größe der erstellten Labyrinthe begrenzt ist. Tatsächlich ist dies ein Binärbaum, wenn wir die obere linke Ecke als Wurzel betrachten und jeder Knoten oder jede Zelle einen eindeutigen übergeordneten Knoten hat, der eine Zelle darüber oder links davon ist. Auf Binärbäumen basierende Labyrinthe unterscheiden sich von idealen Standardlabyrinthen, da mehr als die Hälfte der Zelltypen in ihnen nicht existieren können. Zum Beispiel wird es niemals Kreuzungen in ihnen geben, und alle Sackgassen haben Passagen, die nach oben oder links und niemals nach unten oder rechts führen. Labyrinthe haben in der Regel Passagen, die diagonal von links oben nach rechts unten führen, und es ist viel einfacher, sich von rechts unten nach links oben zu bewegen. Sie können sich immer nach oben oder links bewegen, aber niemals gleichzeitig in beide Richtungen, sodass Sie sich immer deterministisch diagonal nach oben und links bewegen können, ohne auf Barrieren zu stoßen. Sie haben die Möglichkeit zu wählen und in Sackgassen zu geraten, indem Sie sich nach unten und rechts bewegen. , , , .
• 
  
  Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .

Algorithmus	% Sackgassen	Typ	Priorität	Keine Voreingenommenheit?	Homogen?	Die Erinnerung	Zeit	% Lösung
Einzelne Route	0	Baum	Die Wände	Ja	Niemals	N ^ 2	379	100,0
Rekursiver Backtracker	10	Baum	Gehwege	Ja	Niemals	N ^ 2	27	19.0
Jagen und töten	11 (21)	Baum	Gehwege	Ja	Niemals	0	100 (143)	9,5 (3,9)
Rekursive Division	23	Baum	Die Wände	Ja	Niemals	N *	10	7.2
Binärer Baum	25	Viele	Beides	Nein	Niemals	0 *	10	2.0
Sidewinder	27	Viele	Beides	Nein	Niemals	0 *	12	2.6
Eller-Algorithmus	28	Viele	Beides	Nein	Nein	N *	20	4,2 (3,2)
Wilson-Algorithmus	29	Baum	Beides	Ja	Ja	N ^ 2	48 (25)	4.5
Aldous-Broder-Algorithmus	29	Baum	Beides	Ja	Ja	0	279 (208)	4.5
Kraskal-Algorithmus	30	Viele	Beides	Ja	Nein	N ^ 2	33	4.1
Prima-Algorithmus (wahr)	30	Baum	Beides	Ja	Nein	N ^ 2	160	4.1
Prima-Algorithmus (vereinfacht)	32	Baum	Beides	Ja	Nein	N ^ 2	59	2.3
Prima-Algorithmus (modifiziert)	36 (31)	Baum	Beides	Ja	Nein	N ^ 2	30	2.3
Baum wächst	49 (39)	Baum	Beides	Ja	Nein	N ^ 2	48	11.0
Wald wächst	49 (39)	Beides	Beides	Ja	Nein	N ^ 2	76	11.0

Diese Tabelle fasst die Eigenschaften der oben beschriebenen Algorithmen zur Erzeugung idealer Labyrinthe zusammen. Zum Vergleich wurde ein Einweg-Labyrinthalgorithmus hinzugefügt (theoretisch sind Einweg-Labyrinthe ideal). Spaltenerklärung:

• : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
• : : , , . , , , , . , , .
• : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
• : , . , . Sidewinder , . , . Hunt and Kill , , , .
• : . «» , . «» , , . «» , , . , .
• : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
• : , , , . , ( 10), . 100x100 Daedalus. , , , .
• : , , . , 100x100 . . «» . , . , . , , , .

Es gibt viele Möglichkeiten, Labyrinthe zu lösen, und jede hat ihre eigenen Eigenschaften. Hier ist eine Liste spezifischer Algorithmen:

• 
  
  Folgen entlang der Wände (Wall Follower) : . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
• 
  
  : , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
• 
  
  : (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
• 
  
  Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
• 
  
  (Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
• 
  
  (Dead end filler) : . , . , , . , . , , . , , .
• 
  
  Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
• 
  
  Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
• 
  
  Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
• 
  
  (Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
• 
  
  (Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .
• Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
• Random mouse: , , .. , . 180 , . , , . , , .

		?	Priorität	?	?	?	?
Random Mouse	1	Nein	Du bist	/	Nein	Ja	Nein
Wall Follower	1	Nein	Du bist	/	Ja	Ja	Ja
	1	Nein	Du bist	/	Ja	Ja	Ja
	1	Ja	+	Nein	Ja	Nein	Ja
Recursive Backtracker	1	Ja	Du bist	Nein	Ja	Nein	Ja
Tremo-Algorithmus	1	Ja	Du bist	Innen / über	Nein	Nein	Ja
Sackgasse Füller	Alle +	Nein	Labyrinth	Über	Nein	Ja	Ja
Sackgasse Füller	Alle +	Nein	Labyrinth	Über	Nein	Ja	Ja
Sackgasse Sealer	Alle +	Ja	Labyrinth	Nein	Nein	Nein	Ja
Sackgassenfüller	Alle	Ja	Labyrinth	Über	Nein	Ja	Nein
Kollisionslöser	Alles am kürzesten	Ja	Sie +	Nein	Nein	Nein	Ja
Suche nach kürzesten Wegen	Alles am kürzesten	Ja	Sie +	Nein	Ja	Nein	Ja
Suche nach dem kürzesten Weg	1 kürzeste	Ja	Sie +	Nein	Ja	Nein	Ja

In dieser Tabelle sind die Eigenschaften der oben beschriebenen Labyrinthlösungsalgorithmen kurz aufgeführt. Nach diesen Kriterien ist es möglich, Algorithmen zur Lösung von Labyrinthen zu klassifizieren und zu bewerten. Spaltenerklärungen:

• : , . . , () . Dead end filler cul-de-sac filler ( blind alley sealer ) , , , «+».
• : . Random mouse «», , wall follower «», , . dead end filler cul-de-sac filler «», .
• : : «» ( ) . , ( «») («+») . , .
• : , , . , «», , ( ), , , , . .
• : . , , , , . Wall follower, . Recursive backtracker shortest path(s) finder .
• : . .
• Schnell: Wird der Entscheidungsprozess als schnell angesehen? Die effizientesten Algorithmen reichen aus, um jede Zelle des Labyrinths nur einmal zu betrachten, oder sie können Teile davon vollständig überspringen. Die Laufzeit sollte proportional zur Größe des Labyrinths oder O (n ^ 2) sein, wobei n die Anzahl der Zellen entlang einer Seite ist. Zufällige Mäuse sind langsam, da ihre Fertigstellung nicht garantiert ist und der Sackgassenfüller möglicherweise das Labyrinth von jeder Gabel löst.

Andere Operationen mit Labyrinthen

Neben dem Erstellen und Lösen von Labyrinthen können Sie mit ihnen auch andere Vorgänge ausführen:

• 
  
  : « », , Fill FloodFill. FloodFill , , . , , FloodFill , . , , FloodFill , , . «» .
• 
  
  (Isolation remover): , , . , . , . ( , ) , . , , . .
• 
  
  : , , . , , . , . ( , ) . , , , . , .
• 
  
  : , . , , , , . , , . , . , blind alley sealer ( , ). , , .

• Daedalus : Daedalus, Windows. Daedalus .