Gugologie (dies ist kein Tippfehler) für Programmierer

Es ist schwieriger, über Mathematik zu schreiben (so dass es interessant ist) als über Physik. Ich hoffe jedoch, dass Sie zumindest die Beispiele für verrückte C-Programme lesen.


Monster können aus völlig harmlosen Dingen wachsen. Nehmen Sie zum Beispiel das Spiel der Teilzeichenfolgen. Wir schreiben eine Folge von Buchstaben a und b und wählen Teilzeichenfolgen von Zeichen 1 bis Zeichen 2, von 2 bis 4, von drei bis 6, von n bis 2n aus, bis die Länge der Hauptzeichenfolge ausreicht. Unsere Aufgabe ist es sicherzustellen, dass in diesen Teilzeichenfolgen die kürzeren nicht mehr eingehen. Ich habe sogar einen SQL-Parser geschrieben:

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 

Hier ist eine Beispielausgabe:



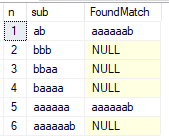
Wie Sie sehen können, haben die Teilzeichenfolgen 1 und 5 den Test nicht bestanden. Wir können das letzte Zeichen entfernen und die resultierende 11-stellige Zeichenfolge 'abbbaaaaaaaa' besteht den Test. Es stellt sich heraus, dass dies die längste mögliche Zeichenfolge im zweistelligen Alphabet ist, die diese Bedingung erfüllt.

Für ein Alphabet mit einem Zeichen beträgt die maximale Zeichenfolgenlänge 3 und dann aus rein technischen Gründen. Es stellt sich heraus, dass die maximale Länge für ein Alphabet mit einer beliebigen Anzahl von Buchstaben endlich ist. Also haben wir:

$$

$$f (1) = 3$$

$$

$$f (2) = 11$$

$$

$$f (3) = ???$$

Testen Sie Ihre Intuition darüber, wie lange eine Zeichenfolge in einem aus drei Buchstaben bestehenden Alphabet bestehen kann. 100? 1000? In der Tat viel mehr als Googol und viel mehr als GoogolPlekh.

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

Und ich muss Zeit aufwenden, um die Stärke der Schützen zu zeigen.

Pfeile (Hyperoperation)

Wir verwenden die Multiplikation, um nicht viele Additionsoperationen zu schreiben:

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

Wir verwenden die Potenzierung, um nicht viele Multiplikationen zu schreiben:

$$

$$2 ^ 3 = 2 * 2 * 2$$

Betrachtet man die Addition als eine Operation der Stufe 0, die Multiplikation als 1, die Exponentiation als 2, so kann man beispielsweise die Operation "Pfeil" einführen

$$

$$3 \ uparrow 3 = 3 ^ {(3 ^ 3)} = 3 ^ {27} = 7'625'597'484'987$$

Beachten Sie, dass Klammern hier bereits wichtig sind. Die nächste Stufe ist die Zwei-Pfeil-Operation:

$$

$$3 \ uparrow \ uparrow 3 = 3 \ uparrow (3 \ uparrow 3) = 3 \ uparrow 7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

Die letzte Dreifachpyramide hat eine Höhe von 7 Milliarden, und diese Zahl ist bereits viel, viel größer als Googol und Googolpleks. Wir bezeichnen diese riesige Zahl als Dunkelheit (es war eine solche Zahl in der alten russischen Sprache) und versuchen, einen weiteren Schritt zu tun:

$$

$$3 \ uparrow ^ 3 3 = 3 \ uparrow \ uparrow \ uparrow 3 = 3 \ uparrow \ uparrow (3 \ uparrow \ uparrow 3) = 3 \ uparrow \ uparrow {dunkel} = 3 \ uparrow 3 \ uparrow 3 ... \ uparrow 3$$

(und so oft) ... Man kann sich schon vorstellen, wie groß diese Zahl ist. Bitte beachten Sie, dass wir bei vielen Pfeilen oben einen Repeater schreiben. So können Sie verstehen, wie großartig

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

Und mehr

Mit Pfeilen wird sozusagen nur die kleinste der großen Zahlen erstellt. Die Wachstumsrate von Funktionen wird in einem bestimmten Maßstab gemessen - durch Vergleich mit schnell wachsenden Funktionen . Die erste Funktion in dieser Hierarchie entspricht der Addition, die zweite der Multiplikation, die dritte dem Pfeil und die n-ten bis n-2 Pfeile (ungefähr, nicht genau). Aber du kannst definieren

$$

$$f_w (n) = f_n (n)$$

Eine solche Funktion für n = 3 ist vergleichbar mit einem Pfeil, für n = 4 mit zwei Pfeilen, und wenn der Parameter n wächst, übertrifft sie das Wachstum der Funktion mit einer beliebigen statischen Anzahl von Pfeilen.

Sie können noch weiter gehen: $$$f_w, f_ {w + 1}, f_ {w + n}, f_ {w2}, f_ {w ^ 2}, f_ {w ^ w}, f_ {w ^ {w ^ {w}}}, f_ \ epsilon$ Diese Funktionen werden durch Ordnungszahlen oder in der russischen Literatur durch Ordnungszahlen indiziert. Das Bild mit der Struktur der anfänglichen Ordnungszahlen geht dem Artikel voraus, aber sie erstrecken sich viel weiter und beginnen weiter

Kleine Mystik

Die endlose Omega-Pyramide gibt eine Ordnungszahl $$$\ epsilon_0$ . Lesen Sie mehr über die Funktion, deren Wachstum anhand dieser Ordnungszahl gemessen wird. Es stellt sich heraus, dass eine Funktion so schnell wächst, dass die formale Arithmetik im Prinzip nicht beweisen kann, dass eine solche Funktion überhaupt definiert ist!

Natürlich wissen Sie über Godels Theorem, dass es unbeweisbare Aussagen gibt. Das einzige Beispiel für eine solche Aussage ist jedoch in der Regel Gödels Konstruktion selbst („Ich bin unbeweisbar“). Der Satz von Goodstein ist ein gutes Beispiel für eine solche Aussage.

Darüber hinaus stellt sich heraus, dass Ordnungszahlen in gewisser Weise die Kraft von Theorien messen . Die "Stärke" der formalen Arithmetik ist $$$\ epsilon_0$ hat die vereinfachte Kripke-Plateka-Mengenlehre die Stärke der Feferman-Schutte- Ordnungszahl usw.

Tin - Maths Tourniquet - C Sprachwettbewerb

Ein Wettbewerb wurde abgehalten, um große Zahlen zu generieren. Nein, die Programmierung für eine Turing-Maschine ist immer noch zu grausam, daher wurde C für eine abstrakte unendliche Maschine mit sizeof (int) = unendlich verwendet. Sie können auch malloc () verwenden, und die Speicherkapazität ist wie beim Stapel unbegrenzt. Nur die Programmlänge war begrenzt - das Programm musste in 512 Bytes (ohne Leerzeichen) passen, aber die Verwendung eines Präprozessors (#define) war erlaubt.

Die Ergebnisse werden auf der Mathematik-Website veröffentlicht . Schauen Sie sich gleichzeitig das Design der Website eines echten Mathematikers an. Die Ergebnisse sind hier . Hier ist der Text des Programms, der den zweiten Platz belegte und die Nummer ungefähr angibt

$$

$$f_ {w ^ w} (10 ^ {500})$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} 

Der Programmtext des Gewinners ist länger, ich wollte nur zeigen, wo er beginnt:

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} 

Aber selbst der Veranstalter des Wettbewerbs fand es schwierig zu bewerten, wie groß die Zahl war ( sehr groß geschrieben ).

Beschäftigte Biber

Okay, genug, um mit winzigen Zahlen fertig zu werden, machen wir große. Stellen Sie sich vor, dass ein universeller Wettbewerb organisiert wurde, um ein Programm zur Generierung der größten Anzahl zu schreiben. Da die Anzahl der Programme nicht länger als 512 Zeichen ist, gibt es natürlich immer einen absoluten Gewinner. Bezeichnen wir es als BB (512) - beschäftigte Biberfunktion .

Es ist klar, dass BB (1024) >> BB (512). Aber wie schnell wächst die BB-Funktion? Es stellt sich heraus, dass es schneller wächst als alles, was wir getroffen haben. Die BB-Funktion selbst ist algorithmisch nicht lösbar und kann nicht auf einem Computer berechnet werden. Mit zunehmender Länge des gültigen Programms können wir jedoch immer mehr neue Ideen umsetzen. BB wächst also schneller als jede algorithmisch entscheidbare Funktion.

GROSSER FUSS

Okay, genug, um mit winzigen Zahlen fertig zu werden, machen wir große. Ah, habe ich das schon gesagt? Es wäre cool, BB (BB (n)) laufen zu lassen. Da BB jedoch nicht berechenbar ist, gibt es technische Schwierigkeiten (eine solche Funktion ist in Turing-Maschinen mit Orakeln berechenbar - um Orakel nicht mit Oracle DBMS zu verwechseln).

Aber Sie können es einfacher machen, anstatt eines Programms eine Formel mit Quantifizierern der Länge n zu betrachten. Eine Quantifiziererformel spielt keine Rolle, ob etwas berechenbar ist oder nicht. Sie können also mindestens die Funktion BB (1.000.000.000) übernehmen und sie auf sich selbst anwenden (BB (BB (1.000.000))). Und das ist nur das, was mir zuerst in den Sinn kam.

Die größte Zahl, die durch eine Formel mit höchstens n Zeichen angegeben werden kann, wird mit FOOT (n) bezeichnet.

$$

$$BIG FOOT = FOOT ^ {10} (10 ^ {100})$$

PS

Für den nächsten Artikel möchte ich verstehen, worauf ich mich konzentrieren soll. Nehmen Sie bitte an der Umfrage teil