Verringerung der Stichprobengröße experimenteller Daten ohne Informationsverlust

Was ist das Problem der experimentellen Datenhistogramme?

Die Grundlage des Produktqualitätsmanagements eines Industrieunternehmens ist die Erfassung experimenteller Daten mit deren anschließender Verarbeitung.

Die anfängliche Verarbeitung der experimentellen Ergebnisse beinhaltet den Vergleich der Hypothesen über das Gesetz der Datenverteilung, das mit dem kleinsten Fehler eine Zufallsvariable über die beobachtete Stichprobe beschreibt.

Hierzu wird die Probe in Form eines Histogramms bestehend aus dargestellt $$$k$ Säulen in Längenintervallen aufgebaut $$$d$ .

Die Identifizierung der Form der Verteilung der Messergebnisse erfordert auch eine Reihe von Problemen, deren Lösungseffizienz für verschiedene Verteilungen unterschiedlich ist (z. B. unter Verwendung der Methode der kleinsten Quadrate oder Berechnung der Entropieschätzungen).

Darüber hinaus ist auch die Identifizierung der Verteilung erforderlich, da die Streuung aller Schätzungen (Standardabweichung, Überschuss, Kurtosis usw.) auch von der Form des Verteilungsgesetzes abhängt.

Der Erfolg der Identifizierung der Verteilungsform experimenteller Daten hängt von der Stichprobengröße ab. Wenn diese klein ist, werden die Verteilungsmerkmale durch die Zufälligkeit der Stichprobe selbst maskiert. In der Praxis ist es aus verschiedenen Gründen nicht möglich, eine große Stichprobengröße bereitzustellen, beispielsweise mehr als 1000.

In einer solchen Situation ist es wichtig, die Probendaten bestmöglich in den Intervallen zu verteilen, wenn die Intervallreihen für weitere Analysen und Berechnungen erforderlich sind.

Für eine erfolgreiche Identifizierung ist es daher notwendig, das Problem der Zuweisung der Anzahl von Intervallen k zu lösen

A. Hald in dem Buch [1] überzeugt weitgehend davon, dass es eine optimale Anzahl von Gruppierungsintervallen gibt, wenn die schrittweise Hüllkurve des Histogramms, das auf diesen Intervallen aufgebaut ist, der glatten Verteilungskurve der allgemeinen Bevölkerung am nächsten kommt.

Eines der praktischen Anzeichen für die Annäherung an das Optimum ist das Verschwinden von Einbrüchen im Histogramm, und dann wird das größte k als nahe am Optimum betrachtet, bei dem das Histogramm immer noch einen glatten Charakter behält.

Offensichtlich hängt die Art des Histogramms von der Konstruktion von Intervallen ab, die zu einer Zufallsvariablen gehören, aber selbst im Fall einer einheitlichen Partition ist eine zufriedenstellende Methode für diese Konstruktion immer noch nicht verfügbar.

Die Partition, die als korrekt angesehen werden könnte, führt dazu, dass der Approximationsfehler durch die stückweise konstante Funktion der vermeintlich kontinuierlichen Verteilungsdichte (Histogramm) minimal ist.

Die Schwierigkeiten werden durch die Tatsache verursacht, dass die geschätzte Dichte unbekannt ist, daher beeinflusst die Anzahl der Intervalle stark die Form der Häufigkeitsverteilung der endgültigen Probe.

Bei einer festen Stichprobenlänge führt die Vergrößerung der Verteilungsintervalle nicht nur zu einer Verfeinerung der empirischen Wahrscheinlichkeit, in sie zu fallen, sondern auch zu einem unvermeidlichen Informationsverlust (sowohl im allgemeinen Sinne als auch im Sinne der Wahrscheinlichkeitsdichteverteilungskurve), weshalb bei weiterer ungerechtfertigter Vergrößerung die untersuchte Verteilung zu stark geglättet wird .

Sobald dies geschehen ist, verschwindet die Aufgabe der optimalen Aufteilung des Bereichs unter dem Histogramm nicht aus dem Sichtfeld der Spezialisten, und bis die einzig festgelegte Meinung zu ihrer Lösung erscheint, bleibt die Aufgabe relevant.

Auswahl der Kriterien zur Bewertung der Qualität des Histogramms der experimentellen Daten

Das Pearson-Kriterium erfordert bekanntlich die Aufteilung der Stichprobe in Intervalle - in diesen wird der Unterschied zwischen dem angenommenen Modell und der verglichenen Stichprobe bewertet.

$$$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

wo: $$$E_ {j}$ - experimentelle Frequenzen $$$(n_ {j})$ ;; $$$M_ {j}$ - Frequenzwerte in derselben Spalte, m-Anzahl der Histogrammspalten.

Die Anwendung dieses Kriteriums bei Intervallen konstanter Länge, die üblicherweise zur Erstellung von Histogrammen verwendet werden, ist jedoch ineffizient. Daher werden in den Arbeiten zur Wirksamkeit des Pearson-Kriteriums die Intervalle nicht mit gleicher Länge, sondern mit gleicher Wahrscheinlichkeit gemäß dem akzeptierten Modell betrachtet.

In diesem Fall unterscheiden sich jedoch die Anzahl der Intervalle gleicher Länge und die Anzahl der Intervalle gleicher Wahrscheinlichkeit um ein Vielfaches (mit Ausnahme einer gleich wahrscheinlichen Verteilung), so dass man die Zuverlässigkeit der in [2] erhaltenen Ergebnisse bezweifeln kann.

Als Näherungskriterium wird empfohlen, den Entropiekoeffizienten zu verwenden, der wie folgt berechnet wird [3]:

$$$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

$$$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

wo: $$$n_ {i}$ - die Anzahl der Beobachtungen im i-ten Intervall $$$i = 0, ..., m$

Algorithmus zur Bewertung der Qualität des Histogramms experimenteller Daten unter Verwendung des Entropiekoeffizienten und des Moduls numpy.histogram

Die Syntax für die Verwendung des Moduls lautet wie folgt [4]:

numpy.histogram (a, Behälter = m, Bereich = keine, normiert = keine, Gewichte = keine, Dichte = keine)

Wir werden Methoden zum Ermitteln der optimalen Anzahl m von Histogramm-Aufteilungsintervallen betrachten, die im Modul numpy.histogram implementiert sind:

• 'auto' - maximale Bewertungen von 'sturges' und 'fd' sorgen für gute Leistung;
• 'fd' (Freedman Diaconis Estimator) - ein zuverlässiger (emissionsbeständiger) Bewerter, der die Variabilität und Größe der Daten berücksichtigt;
• 'doane' - eine verbesserte Version der Störschätzung, die mit Datensätzen mit einer nicht normalen Verteilung genauer funktioniert;
• 'scott' ist ein weniger zuverlässiger Bewerter, der die Variabilität und Größe der Daten berücksichtigt.
• 'Stein' - Der Bewerter basiert auf einer Gegenprüfung der Schätzung des Quadrats des Fehlers und kann als Verallgemeinerung der Scottschen Regel angesehen werden.
• „Reis“ - Der Gutachter berücksichtigt nicht die Variabilität, sondern nur die Größe der Daten und überschätzt häufig die Anzahl der erforderlichen Intervalle.
• 'sturges' - Die Methode (standardmäßig), bei der nur die Größe der Daten berücksichtigt wird, ist nur für Gaußsche Daten optimal und unterschätzt die Anzahl der Intervalle für große nicht-Gaußsche Datensätze.
• 'sqrt' ist der Quadratwurzelschätzer für die Datengröße, die von Excel und anderen Programmen zur schnellen und einfachen Berechnung der Anzahl der Intervalle verwendet wird.

Um mit der Beschreibung des Algorithmus zu beginnen, passen wir das Modul numpy.histogram () an, um den Entropiekoeffizienten und den Entropiefehler zu berechnen:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h 

Betrachten Sie nun die Hauptstufen des Algorithmus:

1) Wir bilden eine Kontrollprobe (im Folgenden als "große Probe" bezeichnet), die die Anforderungen für den Fehler bei der Verarbeitung experimenteller Daten erfüllt . Aus einer großen Stichprobe bilden wir durch Entfernen aller ungeraden Elemente eine kleinere Stichprobe (im Folgenden als "kleine Stichprobe" bezeichnet);

2) Für alle Bewerter 'auto', 'fd', 'doane', 'scott', 'stone', 'Rice', 'sturges', 'sqrt' berechnen wir den Entropiekoeffizienten ke1 und den Fehler h1 für eine große Stichprobe und den Entropiekoeffizienten ke2 und der Fehler h2 für eine kleine Stichprobe sowie der Absolutwert der Differenz - abs (ke1-ke2);

3) Wir steuern die numerischen Werte der Bewerter in mindestens vier Intervallen und wählen den Bewerter aus, der den Mindestwert der absoluten Differenz liefert - abs (ke1-ke2).

4) Für die endgültige Entscheidung über die Wahl eines Gutachters bauen wir auf einem Histogramm die Verteilungen für die großen und kleinen Stichproben auf, wobei der Gutachter den minimalen abs-Wert (ke1-ke2) und auf dem zweiten mit dem Gutachter den maximalen abs-Wert (ke1-ke2) liefert. Das Auftreten zusätzlicher Sprünge in einer kleinen Stichprobe im zweiten Histogramm bestätigt die richtige Wahl des Bewerters im ersten.

Betrachten Sie die Arbeit des vorgeschlagenen Algorithmus an einer Stichprobe von Daten aus einer Veröffentlichung [2]. Die Daten wurden durch zufällige Auswahl von 80 Rohlingen aus 500 mit anschließender Messung ihrer Masse erhalten. Das Werkstück muss eine Masse in folgenden Grenzen haben: $$$m = 17 _ {- 0,4} ^ {+ 0,6}$ kg Wir bestimmen die optimalen Histogrammparameter anhand der folgenden Auflistung:


Wir bekommen:

Die Standardabweichung für die Probe (n = 80): 0,24
Die mathematische Erwartung für die Stichprobe (n = 80): 17.158
Die Standardabweichung für die Stichprobe (n = 40): 0,202
Die mathematische Erwartung der Stichprobe (n = 40): 17.138
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = auto
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = fd
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = doane
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = scott
ke1 = 1,898, h1 = 0,455, ke2 = 1,934, h2 = 0,39, dke = 0,036, m = Stein
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = Reis
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = Störe
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = sqrt



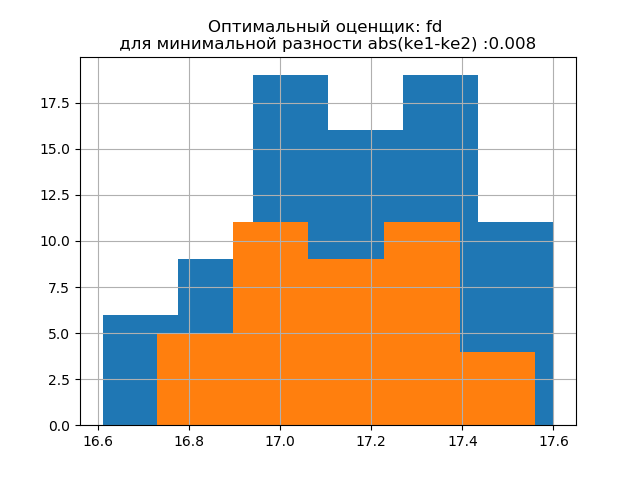
Die Form der Verteilung einer großen Probe ähnelt der Form der Verteilung einer kleinen Probe. Wie aus dem Skript hervorgeht, ist 'fd' ein zuverlässiger (emissionsbeständiger) Bewerter, der die Variabilität und Größe der Daten berücksichtigt. In diesem Fall nimmt der Entropiefehler der kleinen Probe sogar geringfügig ab: h1 = 0,46, h2 = 0,386 mit einer leichten Abnahme des Entropiekoeffizienten von k1 = 1,918 auf k2 = 1,91.



Die Verteilungsmuster von großen und kleinen Proben unterscheiden sich. Wie aus der Beschreibung hervorgeht, ist 'doane' eine verbesserte Version des 'sturges'-Scores, die bei Datensätzen mit einer nicht normalen Verteilung besser funktioniert. In beiden Stichproben liegt der Entropiekoeffizient nahe bei zwei und die Verteilung nahe am Normalen. Das Auftreten zusätzlicher Sprünge in einer kleinen Stichprobe in diesem Histogramm im Vergleich zur vorherigen zeigt zusätzlich die richtige Wahl des Bewerters 'fd' an .

Wir erzeugen zwei neue Stichproben für die Normalverteilung mit den Parametern mu = 20, Sigma = 0,5 und Größe = 100 unter Verwendung der Beziehung:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) 

Die entwickelte Methode ist auf die erhaltene Probe unter Verwendung des folgenden Programms anwendbar:



Wir bekommen:
Die Standardabweichung für die Probe (n = 100): 0,524
Die mathematische Erwartung für die Stichprobe (n = 100): 19.992
Die Standardabweichung für die Probe (n = 50): 0,462
Die mathematische Erwartung der Stichprobe (n = 50): 20.002
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = auto
ke1 = 1,979, h1 = 1,037, ke2 = 1,915, h2 = 0,885, dke = 0,064, m = fd
ke1 = 1,979, h1 = 1,037, ke2 = 1,804, h2 = 0,834, dke = 0,175, m = doane
ke1 = 1,943, h1 = 1,018, ke2 = 1,934, h2 = 0,894, dke = 0,009, m = scott
ke1 = 1,943, h1 = 1,018, ke2 = 1,804, h2 = 0,834, dke = 0,139, m = Stein
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = Reis
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = Störe
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = sqrt



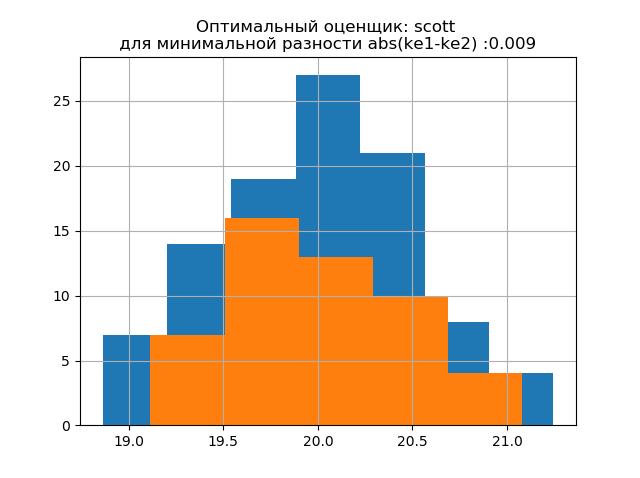
Die Form der Verteilung einer großen Probe ähnelt der Form der Verteilung einer kleinen Probe. Wie aus der Beschreibung hervorgeht, ist 'scott' ein weniger zuverlässiger Bewerter, der die Variabilität und Größe der Daten berücksichtigt. In diesem Fall nimmt der Entropiefehler einer kleinen Probe sogar geringfügig ab: h1 = 1,018 und h2 = 0,894 mit einer leichten Abnahme des Entropiekoeffizienten von k1 = 1,943 auf k2 = 1,934. . Es ist zu beachten, dass wir für die neue Stichprobe die gleiche Tendenz hatten, die Parameter wie im vorherigen Beispiel zu ändern.



Die Verteilungsmuster von großen und kleinen Proben unterscheiden sich. Wie aus der Beschreibung hervorgeht, ist 'doane' eine verbesserte Version der 'sturges'- Schätzung, die bei Datensätzen mit einer nicht normalen Verteilung genauer funktioniert. In beiden Proben ist die Verteilung normal. Das Auftreten zusätzlicher Sprünge in einer kleinen Stichprobe in diesem Histogramm im Vergleich zum vorherigen zeigt zusätzlich die richtige Wahl des "Scott" -Bewerters an.

Verwendung von Anti-Aliasing zur vergleichenden Analyse von Histogrammen

Durch Glätten der Histogramme, die auf den großen und kleinen Stichproben erstellt wurden, können Sie deren Identität unter dem Gesichtspunkt der Beibehaltung der in einer größeren Stichprobe enthaltenen Informationen genauer bestimmen. Stellen Sie sich die letzten beiden Histogramme als Glättungsfunktionen vor:




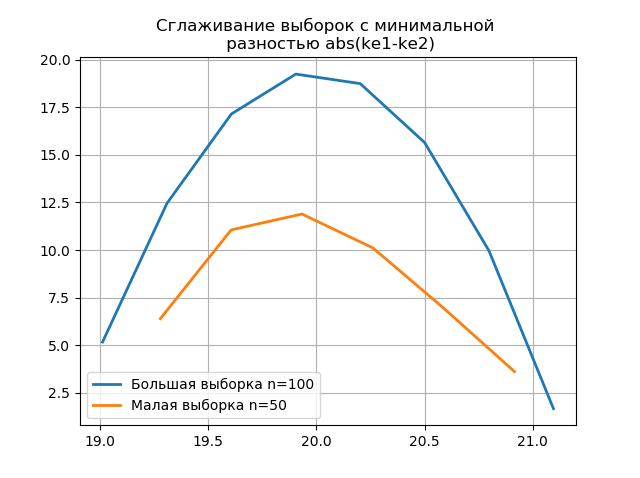
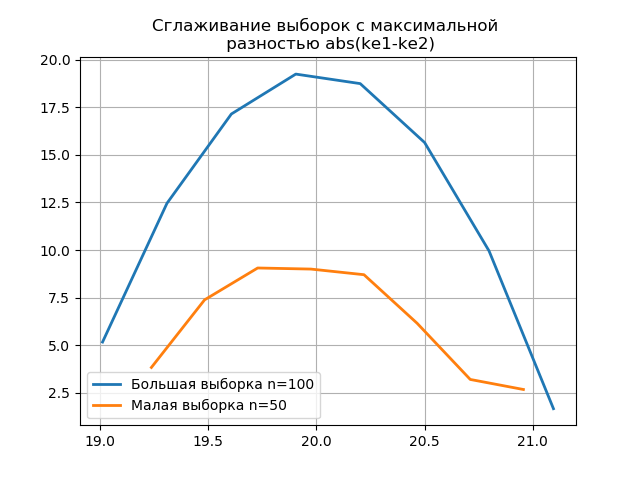
Das Auftreten zusätzlicher Sprünge in einer kleinen Stichprobe in der Grafik eines geglätteten Histogramms im Vergleich zum vorherigen zeigt zusätzlich die richtige Wahl des Scott- Gutachters an.

Schlussfolgerungen

Die im Artikel vorgestellten Berechnungen im Bereich der bei der Herstellung üblichen kleinen Proben bestätigten die Effizienz der Verwendung des Entropiekoeffizienten als Kriterium für die Aufrechterhaltung des Informationsgehalts der Probe bei gleichzeitiger Verringerung ihres Volumens . Die Technik der Verwendung der neuesten Version des Moduls numpy.histogram mit integrierten Evaluatoren wird in Betracht gezogen: "Auto", "FD", "Doane", "Scott", "Stein", "Reis", "Stör", "Sqrt", die für die Optimierung völlig ausreichend sind Analyse experimenteller Daten zu Intervallschätzungen.

Referenzen:

1. Hald A. Mathematische Statistik mit technischen Anwendungen. - Moskau: Verlag. Lit., 1956
2. Kalmykov V.V., Antonyuk F.I., Zenkin N.V.
Bestimmung der optimalen Anzahl experimenteller Datengruppierungsklassen für Intervallschätzungen // South Siberian Scientific Bulletin. - 2014. - Nr. 3. - P. 56-58.
3. Novitsky P. V. Das Konzept des Entropiewertes des Fehlers // Messtechnik. - 1966. - Nr. 7. —S. 11-14.
4.numpy.histogram - NumPy v1.16 Handbuch