Einführung

Wie kann man herausfinden, dass eine Person verstanden hat, was Monaden sind? Er selbst wird Ihnen dies in den ersten 5 Minuten der Kommunikation erzählen und sicherlich versuchen, es zu erklären. Er wird auch einen Text darüber schreiben und ihn, wenn möglich, irgendwo veröffentlichen, damit alle anderen auch verstehen, was Monaden sind.

Unter funktionalen Programmierern, insbesondere auf Haskell, sind Monaden zu einem lokalen Mem geworden. Sie werden oft versucht zu erklären, ausgehend von Sonderfällen und sofort mit Anwendungsbeispielen. Aus diesem Grund versteht der Hörer möglicherweise nicht die Hauptessenz des Konzepts, und Monaden bleiben schwarze Magie oder einfach ein Mittel, um Nebenwirkungen in rein funktionalen Sprachen zu unterdrücken.

Ich werde zuerst über die Grundkonzepte der Kategorietheorie sprechen, und dann werden wir uns aus praktischer Sicht der Definition einer Monade nähern und feststellen, dass tatsächlich sehr viele Programmierer diese mächtige Abstraktion in einer ihrer Erscheinungsformen verwenden.

Meine Präsentation basiert größtenteils auf Bartosz Milewskis Buch "Kategorietheorie für Programmierer", das als eine Reihe von Blog-Posts erstellt wurde , als PDF verfügbar ist und kürzlich in Papierform veröffentlicht wurde.

Die Beispiele werden in Haskell bereitgestellt. Es wird davon ausgegangen, dass der Leser mit der Syntax und den Grundkonzepten der Sprache vertraut ist. In dem erwähnten Buch gibt es Beispiele in C ++, Sie können die Reinheit und Verständlichkeit des Codes vergleichen.

Kategorien

Definition

Die Kategorien selbst sind sehr einfache Konstruktionen. Eine Kategorie ist eine Sammlung von Objekten und Morphismen zwischen ihnen. Morphismen können als unidirektionale Pfeile betrachtet werden, die Objekte verbinden. Im allgemeinen Fall ist nichts über das Wesen der Objekte selbst bekannt. Die Kategorietheorie funktioniert nicht mit Objekten, sondern mit Morphismen bzw. deren Zusammensetzung .

Die folgende Notation wird verwendet:

• Ob _C - Objekte der Kategorie C ;
• Hom _C (A, B) - Morphismen von A nach B;
• g ∘ f ist die Zusammensetzung der Morphismen f und g.

Bei der Definition einer Kategorie unterliegen Morphismen zusätzlichen Einschränkungen:

1. Wenn für ein Morphismuspaar f und g f ein Morphismus von A nach B ist (f ∈ Hom (A, B)), g ein Morphismus von B nach C ist (g ∈ Hom (B, C)), dann existiert eine Zusammensetzung g ∘ f ist ein Morphismus von A nach C (g ∘ f ∈ Hom (A, C)).
2. Für jedes Objekt wird ein Identitätsmorphismus id _A ∈ Hom (A, A) angegeben.

Es gibt zwei wichtige Eigenschaften, die jede Kategorie erfüllen muss (Axiome der Kategorietheorie):

1. Die Assoziativität der Zusammensetzung: h ∘ (g ∘ f) = (h ∘ g) ∘ f;
2. Zusammensetzung mit dem Identitätsmorphismus: Wenn f ∈ Hom (A, B), dann ist f ∘ id _A = id _B ∘ f = f.

Kategorien werden sehr einfach und natürlich als gerichtete Grafiken dargestellt. Grundsätzlich kann jeder orientierte Graph zu einer Kategorie erweitert werden, indem bei Bedarf Zusammensetzungen von Morphismen und identischen Morphismen hinzugefügt werden.

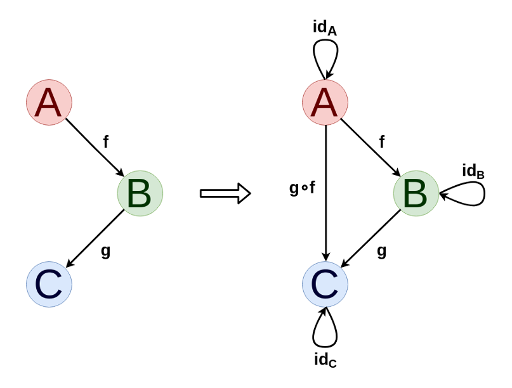
Für jede Kategorie können Sie eine doppelte Kategorie definieren (bezeichnet mit C ^op , in der Morphismen durch Drehen der Pfeile der ursprünglichen Kategorie erhalten werden und die Objekte gleich sind. Auf diese Weise können wir doppelte Aussagen und Theoreme formulieren, deren Wahrheit sich nicht ändert, wenn die Pfeile invertiert werden.

Objekte und Morphismen bilden nicht notwendigerweise Mengen (im klassischen Sinne aus der Mengenlehre), daher wird im allgemeinen Fall der Ausdruck "Klasse von Objekten" verwendet. Kategorien, in denen Klassen von Objekten und Morphismen noch Mengen sind, werden als kleine Kategorien bezeichnet . Weiter werden wir nur mit ihnen arbeiten.

Typen und Funktionen

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

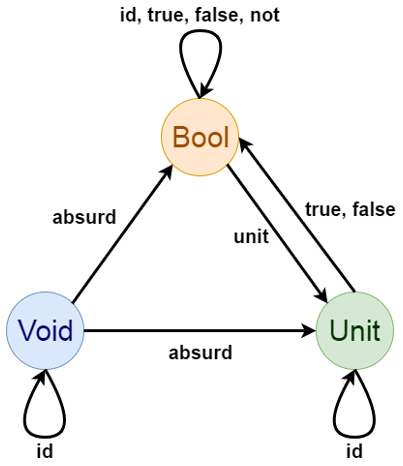
Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

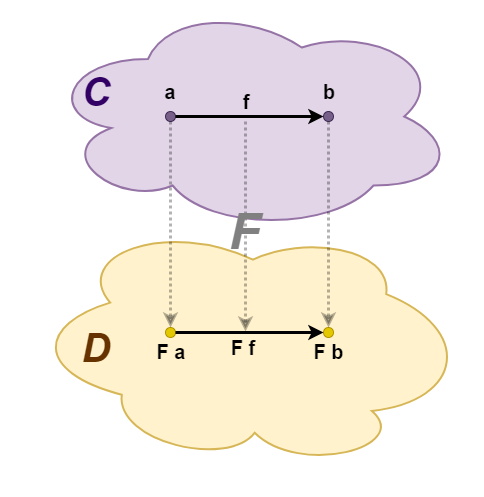
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

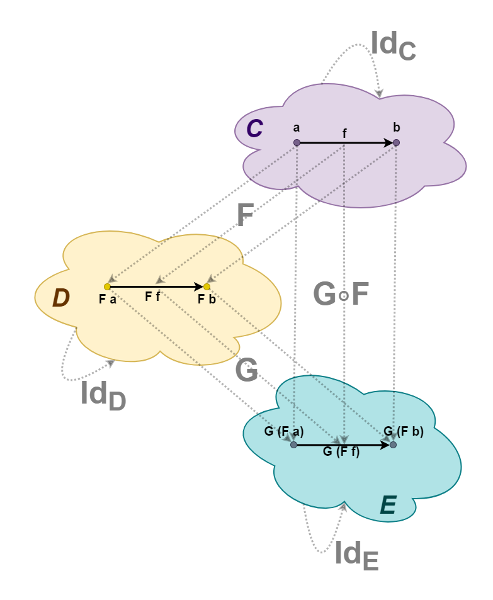
, , -, — (). , Cat ( ).

Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .