🏆 🌋 🤚🏽 Neuronale Quantenzustände - Darstellung einer Wellenfunktion durch ein neuronales Netzwerk 🚖 🍭 👺

In diesem Artikel werden wir die ungewöhnliche Anwendung neuronaler Netze im Allgemeinen und begrenzte Boltzmann-Maschinen im Besonderen zur Lösung zweier komplexer Probleme der Quantenmechanik betrachten - das Finden der Grundzustandsenergie und die Annäherung der Wellenfunktion eines Vielkörpersystems.

Wir können sagen, dass dies eine kostenlose und vereinfachte Nacherzählung eines Artikels [2] ist, der 2017 in Science veröffentlicht wurde, sowie einiger nachfolgender Arbeiten. Ich fand keine populärwissenschaftlichen Darstellungen dieser Arbeit in russischer Sprache (und nur in dieser englischen Version), obwohl sie mir sehr interessant erschien.

Minimale wesentliche Konzepte aus der Quantenmechanik und dem tiefen Lernen

Ich möchte sofort darauf hinweisen , dass diese Definitionen extrem vereinfacht sind . Ich bringe sie für diejenigen, für die das beschriebene Problem ein dunkler Wald ist.

Ein Zustand ist einfach eine Reihe physikalischer Größen, die ein System beschreiben. Für ein im Weltraum fliegendes Elektron sind es beispielsweise seine Koordinaten und sein Impuls, und für ein Kristallgitter ist es eine Reihe von Spins von Atomen, die sich in seinen Knoten befinden.

Die Wellenfunktion des Systems ist eine komplexe Funktion des Systemzustands. Eine bestimmte Blackbox, die eine Eingabe akzeptiert, z. B. eine Reihe von Drehungen, aber eine komplexe Zahl zurückgibt. Die für uns wichtige Haupteigenschaft der Wellenfunktion ist, dass ihr Quadrat der Wahrscheinlichkeit dieses Zustands entspricht:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

Es ist logisch, dass das Quadrat der Wellenfunktion auf Eins normiert werden sollte (und dies ist auch eines der wesentlichen Probleme).

Hilbert-Raum - in unserem Fall ist eine solche Definition ausreichend - der Raum aller möglichen Zustände des Systems. Für ein System mit 40 Drehungen, das die Werte +1 oder -1 annehmen kann, ist beispielsweise der Hilbert-Raum alles

2^{40}

$2 ^ {40}$ mögliche Bedingungen. Für Koordinaten, die Werte annehmen können

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ ist die Dimension des Hilbert-Raumes unendlich. Es ist die enorme Dimension des Hilbert-Raums für alle realen Systeme, die das Hauptproblem darstellt, das es nicht erlaubt, Gleichungen analytisch zu lösen: Dabei gibt es Integrale / Summationen über den gesamten Hilbert-Raum, die nicht „frontal“ berechnet werden können. Eine merkwürdige Tatsache: Während des gesamten Lebens des Universums kann man nur einen kleinen Teil aller möglichen Zustände treffen, die im Hilbert-Raum enthalten sind. Dies wird sehr gut durch ein Bild aus einem Artikel über Tensor Networks [1] veranschaulicht, der schematisch den gesamten Hilbert-Raum und jene Zustände darstellt, die nach einem Polynom aus der Eigenschaft der Komplexität des Raums (Anzahl von Körpern, Partikeln, Spins usw.) erfüllt werden können.

Eine begrenzte Boltzmann-Maschine - wenn auch schwer zu erklären, handelt es sich um ein ungerichtetes grafisches Wahrscheinlichkeitsmodell, dessen Einschränkung die bedingte Unabhängigkeit der Wahrscheinlichkeiten von Knoten einer Schicht von Knoten derselben Schicht ist. Wenn auf einfache Weise, dann ist dies ein neuronales Netzwerk mit einer Eingabe und einer verborgenen Schicht. Die Werte der Ausgabe von Neuronen in der verborgenen Schicht können 0 oder 1 sein. Der Unterschied zum üblichen neuronalen Netzwerk besteht darin, dass die Ausgaben der Neuronen der verborgenen Schicht Zufallsvariablen sind, die mit einer Wahrscheinlichkeit ausgewählt werden, die dem Wert der Aktivierungsfunktion entspricht:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

s i g m a

$\ sigma$ - Sigmoid-Aktivierungsfunktion ,

b_{i}

$b_i$ - Offset für das i-te Neuron,

W

$W$ - das Gewicht des neuronalen Netzes,

s_{j}

$s_j$ - sichtbare Schicht. Begrenzte Boltzmann-Maschinen gehören zu den sogenannten "Energiemodellen", da wir die Wahrscheinlichkeit eines bestimmten Zustands einer Maschine mit der Energie dieser Maschine ausdrücken können:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

wobei v und h die sichtbaren und verborgenen Schichten sind, a und b die Verschiebungen der sichtbaren und verborgenen Schichten sind, W die Gewichte sind. Dann ist die Wahrscheinlichkeit des Zustands in folgender Form darstellbar:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

Dabei ist Z der Normalisierungsterm, auch statistische Summe genannt (dies ist erforderlich, damit die Gesamtwahrscheinlichkeit gleich Eins ist).

Einführung

Heute gibt es unter den Spezialisten für tiefes Lernen eine Meinung, die begrenzt ist
Boltzmann-Maschinen (im Folgenden - OMB) sind ein veraltetes Konzept, das bei realen Aufgaben praktisch nicht anwendbar ist. 2017 erschien jedoch ein Artikel [2] in Science, der den sehr effizienten Einsatz von OMB bei Problemen der Quantenmechanik zeigte.

Die Autoren bemerkten zwei wichtige Tatsachen, die offensichtlich erscheinen mögen, aber noch nie jemandem in den Sinn gekommen waren:

OMB ist ein neuronales Netzwerk, das nach dem universellen Theorem von Tsybenko theoretisch jede Funktion mit beliebig hoher Genauigkeit approximieren kann (es gibt immer noch viele Einschränkungen, aber Sie können sie überspringen).
OMB ist ein System, dessen Wahrscheinlichkeit für jeden Zustand eine Funktion der Eingabe (sichtbare Schicht), der Gewichte und der Verschiebungen des neuronalen Netzwerks ist.

Gut und weiter sagten die Autoren: Lassen Sie unser System vollständig durch die Wellenfunktion beschreiben, die die Wurzel der OMB-Energie ist, und die OMB-Eingaben sind die Merkmale unseres Systemzustands (Koordinaten, Drehungen usw.):

P s i (s) = f r a c 1 Z s q r t e^{E (s, h)}

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)}}$

Dabei sind s die Eigenschaften des Zustands (z. B. Backs), h die Ausgänge der verborgenen Schicht von OMB, E die Energie von OMB, Z die Normalisierungskonstante (statistische Summe).

Das war's, der Artikel in Science ist fertig, dann bleiben nur noch wenige kleine Details übrig. Zum Beispiel ist es notwendig, das Problem der nicht berechenbaren Partitionsfunktion aufgrund der großen Größe des Hilbert-Raums zu lösen. Und der Satz von Tsybenko besagt, dass ein neuronales Netzwerk jede Funktion approximieren kann, aber es sagt überhaupt nichts darüber aus, wie ein geeigneter Satz von Netzwerkgewichten und -versätzen dafür gefunden werden kann. Nun, und wie immer beginnt der Spaß hier.

Modelltraining

Jetzt gibt es einige Modifikationen des ursprünglichen Ansatzes, aber ich werde nur den Ansatz aus dem ursprünglichen Artikel betrachten [2].

Herausforderung

In unserem Fall lautet die Trainingsaufgabe wie folgt: eine Annäherung der Wellenfunktion zu finden, die den Zustand mit minimaler Energie am wahrscheinlichsten macht. Dies ist intuitiv klar: Die Wellenfunktion gibt uns die Wahrscheinlichkeit eines Zustands, der Eigenwert des Hamilton-Operators (der Energieoperator oder noch einfachere Energie - dieses Verständnis reicht im Rahmen dieses Artikels) für die Wellenfunktion ist Energie. Alles ist einfach.

In Wirklichkeit werden wir uns bemühen, eine andere Größe zu optimieren, die sogenannte lokale Energie, die immer größer oder gleich der Energie des Grundzustands ist:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

hier

s i g m a

$\ sigma$ Ist unser Zustand

s i g m a^{'}

$\ sigma '$ - alle möglichen Zustände des Hilbert-Raums (in Wirklichkeit werden wir einen näheren Wert betrachten),

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ Ist das Matrixelement des Hamiltonian. Dies hängt zum Beispiel stark vom spezifischen Hamilton-Operator ab, beispielsweise für das Ising-Modell

f (s i g m a)

$f (\ sigma)$ wenn

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ und

- c o n s t

$-const$ in allen anderen Fällen. Hören Sie jetzt hier nicht auf; Es ist wichtig, dass diese Elemente für verschiedene populäre Hamiltonianer gefunden werden können.

Optimierungsprozess

Probenahme

Ein wichtiger Teil des Ansatzes aus dem Originalartikel war der Stichprobenprozess. Eine modifizierte Variante des Metropolis-Hastings- Algorithmus wurde verwendet. Das Fazit lautet:

Wir gehen von einem zufälligen Zustand aus.
Wir ändern das Vorzeichen eines zufällig ausgewählten Spins in das Gegenteil (für die Koordinaten gibt es andere Modifikationen, aber sie existieren auch).
Mit einer Wahrscheinlichkeit von $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Big | ^ 2$ in einen neuen Zustand wechseln.
N-mal wiederholen.

Als Ergebnis erhalten wir eine Reihe von Zufallszuständen, die gemäß der Verteilung ausgewählt werden, die unsere Wellenfunktion uns gibt. Sie können die Energiewerte in jedem Zustand und die mathematische Energieerwartung berechnen

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

Es kann gezeigt werden, dass die Schätzung des Energiegradienten (genauer gesagt der erwartete Wert des Hamilton-Operators) gleich ist:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

Fazit

Dies geht aus einem Vortrag von G. Carleo im Jahr 2017 für die Advanced School on Quantum Science and Quantum Technology hervor. Es gibt Einträge auf Youtube.

Bezeichnen:

D_{k}^{*} (x) = f r a c p a r t i e l l e_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ partielle_ {p_k} \ Psi (x)} {\ Psi (x)}$

Dann:

p a r t i e l l e_{p_{k}} m a t h b b E (H) =

$\ partielle_ {p_k} \ mathbb {E} (H) =$

p a r t i e l l e f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ partielle \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} c a .

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ ca.$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

Dann lösen wir einfach das Optimierungsproblem:

Wir probieren Zustände aus unserer OMB aus.
Wir berechnen die Energie jedes Zustands.
Schätzen Sie den Gradienten.
Wir aktualisieren das Gewicht von OMB.

Infolgedessen tendiert der Energiegradient gegen Null, der Energiewert nimmt ab, ebenso wie die Anzahl der eindeutigen neuen Zustände im Metropolis-Hastings-Prozess, da wir durch Abtasten aus der wahren Wellenfunktion fast immer den Grundzustand erhalten. Intuitiv erscheint dies logisch.

In der ursprünglichen Arbeit wurden für kleine Systeme die Werte der Grundzustandsenergie erhalten, die sehr nahe an den genauen analytisch erhaltenen Werten liegen. Es wurde ein Vergleich mit den bekannten Ansätzen zum Ermitteln der Energie des Grundzustands durchgeführt, und NQS gewann, insbesondere angesichts der relativ geringen Rechenkomplexität von NQS im Vergleich zu den bekannten Methoden.

NetKet - eine Bibliothek aus dem Ansatz der "Erfinder"

Einer der Autoren des Originalartikels [2] entwickelte mit seinem Team die hervorragende NetKet-Bibliothek [3], die einen (meiner Meinung nach) sehr gut optimierten C-Kernel sowie die Python-API enthält, die mit Abstraktionen auf hoher Ebene arbeitet.

Die Bibliothek kann über pip installiert werden. Windows 10-Benutzer müssen das Linux-Subsystem für Windows verwenden.

Betrachten wir die Arbeit mit der Bibliothek als Beispiel für eine Kette von 40 Drehungen mit den Werten + -1 / 2. Wir werden das Heisenberg-Modell betrachten, das benachbarte Wechselwirkungen berücksichtigt.

NetKet verfügt über eine hervorragende Dokumentation, mit der Sie schnell herausfinden können, was und wie zu tun ist. Es gibt viele eingebaute Modelle (Rücken, Bosonen, Ising, Heisenberg-Modelle usw.) und die Möglichkeit, das Modell selbst vollständig zu beschreiben.

Anzahl Beschreibung

Alle Modelle sind grafisch dargestellt. Für unsere Kette ist das eingebaute Hypercube-Modell mit einer Dimension und periodischen Randbedingungen geeignet:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Beschreibung von Hilbert Space

Unser Hilbert-Raum ist sehr einfach - alle Drehungen können entweder +1/2 oder -1/2 annehmen. Für diesen Fall ist das eingebaute Modell für Spins geeignet:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Beschreibung des Hamiltonianers

Wie ich bereits schrieb, ist in unserem Fall der Hamiltonianer der Heisenberg-Hamiltonianer, für den es einen eingebauten Operator gibt:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Beschreibung des RBM

In NetKet können Sie eine vorgefertigte RBM-Implementierung für Spins verwenden - dies ist nur unser Fall. Aber im Allgemeinen gibt es viele Autos, man kann verschiedene ausprobieren.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

Hier ist Alpha die Dichte der Neuronen in der verborgenen Schicht. Für 40 Neuronen des sichtbaren und des Alpha 4 gibt es 160 davon. Es gibt eine andere Möglichkeit, direkt durch die Zahl anzuzeigen. Der zweite Befehl initialisiert Gewichte zufällig aus

N (0, s i g m a)

$N (0, \ sigma)$ . In unserem Fall beträgt Sigma 0,01.

Samler

Ein Sampler ist ein Objekt, das uns von einem Sample aus unserer Distribution zurückgegeben wird, das durch die Wellenfunktion im Hilbert-Raum gegeben ist. Wir werden den oben beschriebenen Metropolis-Hastings-Algorithmus verwenden, der für unsere Aufgabe modifiziert wurde:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

Um genau zu sein, ist der Sampler ein schwierigerer Algorithmus als der oben beschriebene. Hier prüfen wir gleichzeitig bis zu 12 Optionen parallel, um den nächsten Punkt auszuwählen. Aber das Prinzip ist im Allgemeinen dasselbe.

Optimierer

Dies beschreibt den Optimierer, der zum Aktualisieren der Modellgewichte verwendet wird. Basierend auf persönlichen Erfahrungen mit neuronalen Netzen in Bereichen, die ihnen „vertrauter“ sind, ist die beste und zuverlässigste Option der gute alte stochastische Gradientenabstieg mit einem Moment (hier gut beschrieben):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

Schulung

NetKet hat eine Ausbildung sowohl ohne Lehrer (unser Fall) als auch mit einem Lehrer (zum Beispiel die sogenannte „Quantentomographie“, dies ist jedoch das Thema eines separaten Artikels). Wir beschreiben einfach die "Lehrer" und das wars:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

Die Variation Monte Carlo gibt an, wie wir den Gradienten der Funktion bewerten, die wir optimieren. n_smaples ist die Größe des Samples aus unserer Distribution, das der Sampler zurückgibt.

Ergebnisse

Wir werden das Modell wie folgt ausführen:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

Die Bibliothek wird mit OpenMPI erstellt, und das Skript muss folgendermaßen ausgeführt werden: mpirun -n 12 python Main.py (12 ist die Anzahl der Kerne).

Die Ergebnisse, die ich erhalten habe, sind wie folgt:

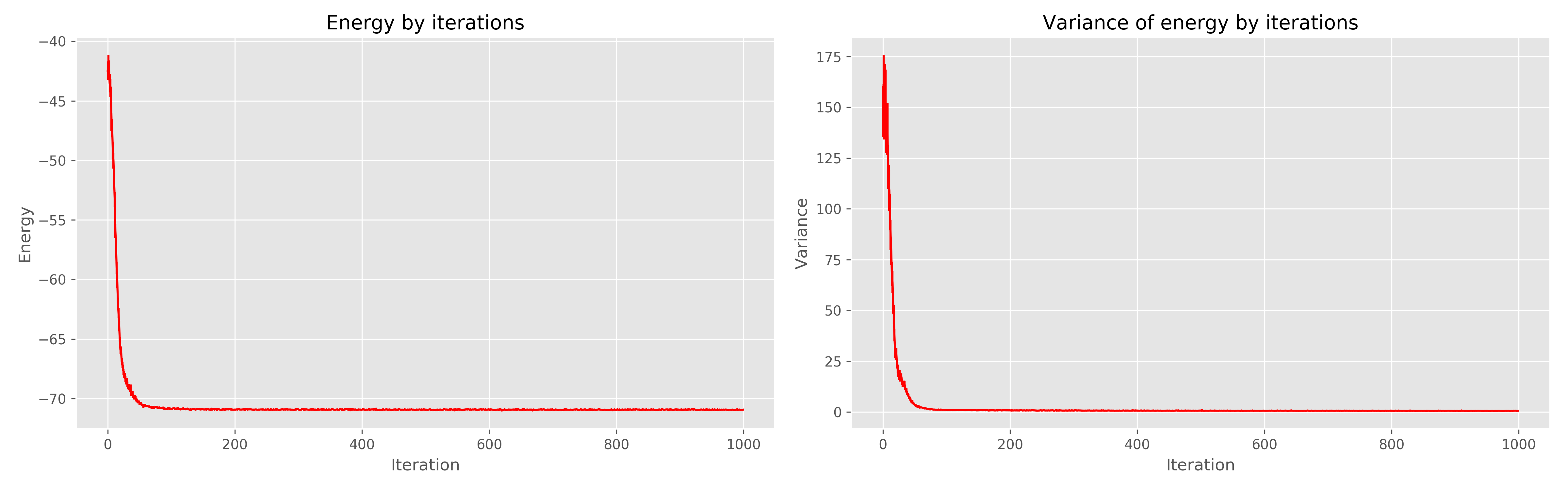
Links ist der Energiediagramm aus der Zeit des Lernens, rechts die Streuung der Energie aus der Zeit des Lernens.
Es ist zu sehen, dass 1000 Epochen eindeutig überflüssig sind, 300 wären genug gewesen. Im Allgemeinen funktioniert es sehr cool, konvergiert schnell.

Literatur

Orús R. Eine praktische Einführung in Tensornetzwerke: Matrixproduktzustände und projizierte verschränkte Paarzustände // Annals of Physics. - 2014 - T. 349. - S. 117-158.
Carleo G., Troyer M. Lösung des Quanten-Vielteilchen-Problems mit künstlichen neuronalen Netzen // Wissenschaft. - 2017. - T. 355. - Nr. 6325. - S. 602-606.
www.netket.org

Neuronale Quantenzustände - Darstellung einer Wellenfunktion durch ein neuronales Netzwerk