Myonenkatalyse in Bezug auf die Quantenchemie. Teil II: elektronisch vs. Myon chemische Bindung

Mnogabukaff, dass die Quantenchemie über das Prinzip der Myonenkatalyse nachdenkt: Wie genau Myon die Temperatur des gewünschten Plasmas senkt. In zwei Teilen (der erste Teil kann hier gelesen werden ).

Das Wesentliche des zweiten Teils ist einfach: Ein Myon ist schwerer als ein Elektron, bietet also eine stärkere chemische Bindung und eine größere Konvergenz der Kerne und senkt dadurch die erforderliche Plasmatemperatur zum Zünden einer thermonuklearen Reaktion.

Aber diejenigen, die sich die Formeln und Grafiken ansehen und die konzeptionelle Essenz der Quantenchemie auf die einfachsten (quasi) Moleküle anwenden möchten, sind unter cat willkommen.

Einführung

Im ersten Teil (siehe hier ) haben wir den Unterschied zwischen einem Wasserstoffatom untersucht $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ von seinem schweren Myon Gegenstück $$$\ mathrm {p} ^ + \ mu ^ -$ : Im zweiten Fall wird das Myon stärker gebunden und sitzt näher am Proton. Gleichzeitig haben wir einige wichtige Dinge untersucht, die wir hier brauchen werden (Formen von Orbitalen und das atomare Einheitensystem).

Im zweiten Teil (d. H. Hier) werden wir versuchen zu verstehen, warum, wie und wie stark die zum Zünden der thermonuklearen Reaktion erforderliche Plasmatemperatur abnimmt. Die Reaktionen, die uns interessieren, sind:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {neue Kernel + Energie}$$

wobei n, m = 1,2,3 Proton, Deuterium bzw. Tritium entsprechen. Natürlich haben diese Kerne eine positive Ladung. Wenn Sie also versuchen, sie näher zu bringen, beginnen sie sich gemäß dem Coulomb-Gesetz abzustoßen (siehe vorherigen Teil ), und dies ist genau die Barriere, die das Einsetzen von Fusionsreaktionen verhindert. Übrigens spielt diese Abstoßung bei nuklearen Zerfallsreaktionen die entgegengesetzte Rolle, da die voneinander abstoßenden Fragmente nach der Trennung vom gemeinsamen Kern zusätzliche kinetische Energie erhalten und diese Energie in Kernkraftwerken erwärmt wird.

Um diese Coulomb-Barriere zu überwinden, ist eine Erhöhung der Plasmatemperatur ( T ) erforderlich, die, wie sich jeder aus dem Schulkurs der MKT erinnert , durch die Formel mit der durchschnittlichen Partikelgeschwindigkeit im Plasma ( v ) verbunden ist

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

wobei m die Masse der Teilchen ist und $$$k_ \ mathrm {B}$ - Boltzmann-Konstante .

Stellen wir uns jedoch vor, wir haben zwei Wasserstoffkerne zu einem bestimmten Teilchen kombiniert, wo sie sich bereits in der Nähe befinden, und daher ist der Rest der Barriere für sie bereits sehr klein. Dann müssten wir diese Partikel deutlich beschleunigen (sprich: wir brauchen niedrigere Temperaturen), um sie zu etwas Neuem zu kombinieren. Und genau diese Rolle sollte ein Zwischenion spielen $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ , ein Analogon des Ions eines Wasserstoffmoleküls $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Nachdem wir die Unterschiede zwischen diesen beiden Partikeln untersucht haben, werden wir feststellen, wie effektiv das Myon die Zündtemperatur der thermonuklearen Fusion senkt.

MILCH MO LKAO Methode

Wir haben also unser molekulares System, bestehend aus 2 Wasserstoffkernen mit einer Ladung + e (ein Elektronenladungsmodulo) und einem Teilchen (Elektron oder Myon) mit einer Ladung - e . Unser System ist isoliert, bis es mit anderen Partikeln kollidiert, und daher kann seine Energie in seine Bestandteile zerlegt werden:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

wo die ersten beiden Begriffe ( $$$T (\ mathrm {H} _1)$ und $$$T (\ mathrm {H} _2)$ ) Ist die kinetische Energie von Wasserstoffkernen der dritte Term ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) Ist die kinetische Energie eines negativen Teilchens (Elektron oder Myon) der vierte Term $$$V (\ mathrm {H_1 \ text {from} H_2})$ Ist die Energie der Coulomb-Abstoßung von Wasserstoff voneinander und die verbleibenden zwei sind die Coulomb-Anziehungskraft des Elektrons / Myons auf jedes der Protonen. Im allgemeinen Fall ist dies ein 3-Körper-Problem, nur ein Quantenproblem. Natürlich ist es sehr schwierig, es in der Stirn zu lösen. Glücklicherweise sind die Kerne mindestens 1800-mal schwerer als das Elektron und 10-mal schwerer als das Myon, sodass sie sich deutlich langsamer bewegen als kleine negative Teilchen. Aus diesem Grund können Sie das Problem zunächst nacheinander lösen: Ermitteln Sie zunächst die Energie von Bewegungen, die nicht mit der Bewegung von Kernen zusammenhängen, d. H. $$$E_ \ mathrm {e}$ und dann volle Energie. Es sieht so aus.

1. Die Anordnung der Wasserstoffkerne relativ zueinander wird ausgewählt, und dies bestimmt die Coulomb-Wechselwirkungen zwischen ihnen und mit dem Elektron / Myon. Coulomb-Potenzial $$$V (R) = k \ frac {q_1q_2} {R}$ hängt nur von Partikelladungen ab $$$q_i$ und der Abstand zwischen ihnen, so dass dieser Wert für alle Wasserstoffisotope gleich ist. Ferner ist das Problem der Bewegung eines Elektrons / Myons im Bereich dieser Kerne gelöst. Dies ist die Aufgabe eines Körpers.
2. Diese Energien $$$E_ \ mathrm {e}$ werden für alle möglichen Anordnungen der Kerne relativ zueinander berechnet, und dies ist die effektive potentielle Bewegungsenergie der Kerne. In unserem Fall müssen wir die Energien in unterschiedlichen Abständen zueinander berechnen, damit das Potenzial für ein Kernpaar immer eindimensional ist. Nun, dann müssen wir nur das Zweikörperproblem der Bewegung zweier Wasserstoffisotope relativ zueinander lösen.

Offensichtlich liegt die Wurzel des Problems bei uns in der Berechnung der Elektronen / Myon-Energie im Bereich der Kerne $$$E_ \ mathrm {e}$ . In der Tat ist dies die chemische Bindung: ein bestimmtes Potential, das die Kerne an bestimmten Stellen zusammenhält. Und genau diese Aufgabe, die Energie der chemischen Bindung zu finden, ist die Hauptaufgabe in der Quantenchemie.

Leider sind sowohl das Myon als auch das Elektron Quantenteilchen. Um diese Energie zu finden, müssen wir daher auf die Methoden der Quantenmechanik zurückgreifen. Tatsächlich ist unser Problem der Bewegung eines Elektrons / Myons im Feld zweier identischer Kerne explizit gelöst (siehe hier ), aber diese Lösung ist sehr kompliziert und das Ergebnis ist nicht so klar wie im Fall eines wasserstoffähnlichen Atoms. Daher werden wir versuchen, einen anderen, ungefähren Ansatz zu zerlegen, der auf alle Systeme anwendbar ist. Dies ist das sogenannte Molekülorbitale Methode als lineare Kombination von Atomorbitalen oder MO LKAO.

Schauen wir uns die Schrödinger-Gleichung für die Bewegung eines Elektrons / Myons im Bereich der Wasserstoffkerne genauer an:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ partielle ^ 2} {\ partielle x ^ 2} + \ frac {\ partielle ^ 2} {\ partielle y ^ 2} + \ frac {\ partielle ^ 2} {\ partielle z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V. } _ \ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

Diese Gleichung wurde im atomaren Einheitensystem geschrieben (siehe PS im vorherigen Teil ), daher beträgt die Ladung des Wasserstoffkerns und des Elektrons / Myons +1, -1, die Elektronenmasse m = 1 und für das Myon m ≈207.

Und wenn Sie genauer hinschauen, können Sie sehen, dass Sie im Hamilton-Operator ein Stück auswählen können, das nur mit der Bewegung eines negativen Teilchens um nur einen der Kerne verbunden ist, der nur der Hamilton-Operator des Wasserstoffatoms ist. Dies kann auf zwei Arten geschehen:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

Außerhalb des Hamiltonian eines wasserstoffähnlichen Atoms ( $$$\ hat {H} _i, \ i = $ 1.$ ) Wir haben immer 2 Teile: die Wechselwirkungsenergie eines Elektrons / Myons mit einem anderen Kern ( $$$\ hat {V} _j$ ) und nukleare Abstoßungsenergie ( $$$\ hat {V} _ \ mathrm {HH}$ ) Die zweite davon beeinflusst die Bewegung von Elektronen überhaupt nicht - es ist nur eine Verschiebung der Energie um einen bestimmten Betrag, aber die Wechselwirkung eines Elektrons mit einem anderen Kern ist eine wichtige Sache.
Wir können uns vorstellen, dass sich unser Teilchen zu jedem Zeitpunkt nur um einen der Kerne dreht und die Wechselwirkung mit dem zweiten nur eine Korrektur ist. Als Rotationsmethode um einen der Kerne können wir annehmen, dass sich das Elektron / Myon im Grundzustand (1s) befindet, dessen Wellenfunktion uns aus dem vorherigen Teil bekannt ist:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

wo $$$R_1$ Ist der Bohr-Radius für ein Teilchen. Im Falle eines Elektrons $$$R_1 = 1$ Bor (das ist der Bohr-Radius für ein Elektron, der ungefähr 0,5 Angström entspricht) und im Fall eines Myons $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
Um die Elektronen / Myon-Wellenfunktion im Bereich von 2 Kernen irgendwie zu approximieren, können wir versuchen, die folgende Darstellung zu nehmen:

$$

$$\ psi \ ca. c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

und dann wird das Problem der Lösung einer komplexen partiellen Differentialgleichung mit uns auf die Suche nach 2 unbekannten Koeffizienten c ₁ und c ₂ reduziert. Dies ist das sehr molekulare Orbital, das als Summe mit den Koeffizienten (eine lineare Kombination der wissenschaftlichen) atomaren 1s-Orbitale dargestellt wird.

Natürlich brauchen wir eine Gleichung für diese Parameter. Und es ist ganz einfach, wenn Sie diese Näherung in die Schrödinger-Gleichung einsetzen $$$\ hat {H} \ psi = E \ psi$ ::

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

Eigentlich wollen wir, dass dieses Verhältnis überall erfüllt wird, damit wir irgendwie die Durchschnittswerte von all dem berechnen können. Wir multiplizieren diese Gleichung links mit $$$<1s_1 |$ und $$$<1s_2 |$ und über alle Koordinaten integrieren. Als Ergebnis erhalten wir ein System von 2 linearen Gleichungen, wobei es notwendig ist, die Koeffizienten c ₁ , c ₂ und Energie E zu finden :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Jeder, der lineare Algebra studiert hat, wird ein verallgemeinertes Eigenvektor-Eigenwert-Problem erkennen. Bevor wir es lösen, werden wir analysieren, was die Elemente der 2 Matrizen, das vorhandene Tuta, sind (und gleichzeitig ihre kurze Bezeichnung mit einem Buchstaben einführen).

• Beginnen wir mit dem einfachsten: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - Dies ist die Normalisierung von Wellenfunktionen, und wie wir uns erinnern, beträgt die Gesamtwahrscheinlichkeit, ein Elektron / Myon zu finden, irgendwo mindestens 1.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - das ist das sogenannte Überlappungsintegral, das zeigt, wie sich 1s-Elektronenwolken für jedes der Atome überlappen.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . Dieses Integral besteht aus mehreren Teilen:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Hier ist es ähnlich:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  d.h. die Energie eines wasserstoffähnlichen Atoms und die Abstoßung des Kerns, skaliert durch das Überlappungsintegral (erster und letzter Term), und sozusagen die Energie des Elektrons / Myons, das von einem Atom zum anderen springt.
  

Finden wir die Ausdrücke für die Energien unseres wasserstoffähnlichen Ions aus der Gleichung, die wie folgt umgeschrieben wurde

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 & S \\ S. & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Um die Energie zu finden, die Sie benötigen, um die Gleichung zu lösen:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

wobei "det" die Determinante bezeichnet (Determinante einer Matrix, auf Russisch).

Die Lösungen dieser quadratischen Gleichung in Bezug auf E sind:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Das erste Stück ist offensichtlich die Energie des Atoms, das zweite ist die internukleare Abstoßung, dieselbe Coulomb-Barriere, die die Entzündung der thermonuklearen Reaktion verhindert, und die letzte komplexe Struktur muss behandelt werden.

Wenn wir die internukleare Abstoßung verwerfen, die nur ein Bezugspunkt für die Elektronen / Myon-Energie ist, erhalten wir zwei Zustände mit Energie

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Da funktionieren beide Wellen $$$| 1s_1 \ rangle$ und $$$| 1s_2 \ rangle$ - positiv und $$$\ hat {V} _i <0$ (weil das negative Teilchen immer zum positiven gezogen wird), dann $$$\ epsilon_ + <- \ frac {m} {2}$ (Energie eines einzelnen Atoms) und $$$\ epsilon _-> - \ frac {m} {2}$ d.h. Wir erhalten ein Standardbild der Molekülorbitale:



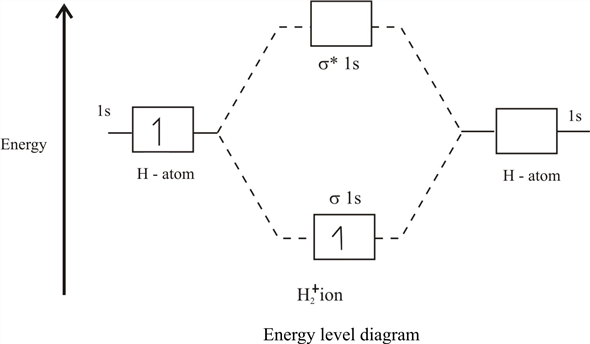
Unteres Orbital mit Energie $$$E _ +$ Bindung genannt, und die Oberseite (mit Energie $$$E _-$ ) - Anti-Bindung oder Lockerung. Wenn ein Elektron / Myon auf dem niedermolekularen Orbital sitzt, profitiert es davon, dass es um 2 Kerne herumfliegt als um einen, und durch seine Bewegung verringert es die Gesamtenergie des Systems. Und dies ist die sehr magische chemische Bindung, die die Abstoßung des Kerns abschirmt und es den Kernen ermöglicht, einige Zeit nebeneinander zu sein.

Und hier müssen die Integrale der chemischen Bindung berechnet werden, um zu verstehen, wie genau die Wasserstoffkerne sein dürfen. Tatsächlich werden alle drei gesuchten Integrale analytisch berechnet, aber es ist furchtbar hämorrhoiden und kompliziert (alle Interessierten siehe Kapitel 9 in Flarys Buch über Quantenchemie ). Daher werden wir einen anderen Weg gehen, einfacher und diese Integrale numerisch unter Verwendung der Monte-Carlo-Methode berechnen.

Metropolis-Methode

Ich sehe es im Text über thermonukleare Energie als sehr logisch an, ihrem Großvater Tribut zu zollen: dem militärischen Atom und insbesondere dem Manhattan-Projekt . Von ihm aus entwickelte sich die Monte-Carlo-Methode und insbesondere der Metropolis-Algorithmus , dessen einer der Autoren, Edward Teller, der „Vater der Wasserstoffbombe“ ist (dh die Person, die die thermonukleare Fusion auf dem Envetok-Atoll gestartet hat).


Im Allgemeinen werden wir das Wesentliche der Methode analysieren. Es ist für die Aufgaben der statistischen Mechanik bestimmt. Die Hauptverteilung darin ist die Boltzmann-Verteilung: Die Wahrscheinlichkeit, ein System in einem bestimmten Zustand zu erkennen, ist $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . Und der beobachtete Wert einiger Parameter A für das System im thermodynamischen Gleichgewicht ist gleich dem Integral

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

Dabei ist q die Koordinaten, die den Zustand des Systems parametrisieren (z. B. die Koordinaten / Impulse der Partikel), und Z ist der Normalisierungsfaktor, der als Partitionsfunktion bezeichnet wird:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

Wenn das System sooooo viele Partikel enthält, ist es völlig unrealistisch, keines der Integrale in der Stirn zu zählen. Die naive Monte-Carlo-Methode, bei der wir einfach eine Reihe zufälliger q- Koordinaten auswählen, liefert auch nichts Sinnvolles, wenn es wirklich mögliche Zustände des Systems gibt, für die die Wahrscheinlichkeit besteht $$$\ exp (- \ beta E)$ merklich ungleich Null, sehr wenige. Und genau für solche Fälle benötigen wir eine Stichprobe nach Signifikanz, in der wir dem Algorithmus erlauben, nur ausreichend wahrscheinliche Stellen im Zustandsraum abzutasten.

Der Metropolis-Algorithmus sieht wie folgt aus.

1. Zu Beginn der Simulation wählen wir im Konfigurationsraum eine Startnäherung aus $$$\ mathbf {q} ^ {(0)}$ und einen Vektor des maximal möglichen Inkrements $$$\ delta \ mathbf {q}$ . Am Anfang berechnen wir die Energie des Systems $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (Lesewahrscheinlichkeit $$$p = \ exp (- \ beta E ^ {(0)})$ )
2. Die neue Konfiguration im n-ten Schritt lautet wie folgt.
   
   1. Berechnen Sie die Energie der Testkonfiguration $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (d. h. Wahrscheinlichkeit $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ )
   2. Und dann vergleichen wir die alte Wahrscheinlichkeit $$$p ^ {(n)}$ mit Versuch $$$p_ \ mathrm {trial}$
      
      
      • wenn die neue Konfiguration eine größere oder gleiche Wahrscheinlichkeit hat ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} \ geq 1$ ) oder äquivalent dazu ist die Energie des neuen Punktes niedriger oder gleich wie beim alten ( $$$E_ \ mathrm {trial} \ leq E ^ {(n)}$ ), dann wird der neue Punkt akzeptiert und das System geht hinein ( $$$q ^ {(n + 1)} = q_ \ mathrm {trial}$ ),
      • wenn die Testkonfiguration energiereicher ist ( $$$E_ \ mathrm {trial}> E ^ {(n)}$ ), was gleichwertig ist $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ In diesem Fall generieren wir eine Zufallszahl $$$P \ in [0; 1)$ aus einer gleichmäßigen Verteilung und vergleichen Sie es mit dem Verhältnis der Wahrscheinlichkeiten, die die Übergangswahrscheinlichkeiten sind. Wenn $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ , dann akzeptieren wir einen neuen Punkt, und wenn nicht ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ), dann lehnen wir ab und das System bleibt in der alten Konfiguration ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. In vielen Schritten gemäß dem obigen Algorithmus wird ein signifikanter (d. H. Wirklich wichtiger) Teil des möglichen Raums von Systemkonfigurationen abgetastet. Das für uns interessante Integral wird nach folgender Formel berechnet:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

So funktioniert der Metropolis-Algorithmus.

Und jetzt wäre es notwendig, es an die Berechnung der 3 Integrale anzupassen, die uns interessieren. Schauen wir sie uns genauer an.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ wo $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - Koordinaten des Elektrons / Myons, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ Sind die Koordinaten der Wasserstoffkerne und $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - Abstände zwischen positiven und negativen Partikeln,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ begrenzt _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ begrenzt _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

Es ist zu sehen, dass, wenn wir die 1s-Funktion eines der Atome für die Wahrscheinlichkeit p berechnen,


dann ist alles andere unter dem Vorzeichen des Integrals (die zweite Wellenfunktion und in 2 von 3 Fällen das Anziehungspotential des Elektrons / Myons zum Kern) eine Funktion, deren Durchschnittswert berechnet wird. Das einzige, was im Gegensatz zur üblichen Berechnung nach der Metropolis-Methode getan werden muss, ist, die Normalisierung der Integrale zu begradigen. Tatsache ist, dass die Standardnormalisierung aktiviert ist

$$

$$Z = \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ border_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

Und wir brauchen Normalisierung dazu $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ wo

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ begrenzt _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ int \ Grenzen _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ Grenzen_ {0} ^ {+ \ infty} \ exp (-2 m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

Dies bedeutet, dass jedes nach der Metropole berechnete Integral mit einem Faktor multipliziert werden muss

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

Dies kann bereits in Form eines bestimmten Skripts angeordnet werden, beispielsweise in Python (der Code befindet sich beispielsweise unten).


Mit solchen Berechnungen können wir endlich die potentiellen Energien im Wasserstoffion vergleichen $$$\ mathrm {H} _2 ^ +$ und sein Myon-Gegenstück.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ vs. $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

Mit einem Skript können wir also die Oberfläche der potentiellen Energie der Annäherung der Wasserstoffkerne berechnen, die durch ein Elektron und ein Myon gebunden sind. Als Energiereferenzpunkt nehmen wir Atome, die unendlich voneinander verdünnt sind (d. H. $$$-m / 2$ , was gleich dem Potential im Abstand zwischen den Kernen ist $$$R = + \ infty$ )

Im Falle eines Elektrons sieht das Potential nahe dem Minimum folgendermaßen aus:



Das Minimum tritt in einem Abstand von ungefähr 2 Bor auf (d. H. Ungefähr die Summe von 2 Atomradien), und die Dissoziationsenergie des Moleküls in Fragmente beträgt ungefähr 0,06 Hartree, was einer Erwärmung auf ungefähr 20.000 Kelvin entspricht (oder Celsius, hier spielt es keine Rolle). Um Energien umzuwandeln, empfehle ich die Verwendung solcher Online-Ressourcen.

Eine ähnliche Situation mit einem muonal gebundenen Wasserstoffion:



Da der Bohr-Radius für Myonenwasserstoff kleiner ist (siehe vorherigen Teil ), sitzen die Wasserstoffkerne bei der minimalen potentiellen Energie auch etwa 200-mal näher. Die Abbauenergie dieses Moleküls beträgt bereits mehr als 10 Hartree, was einer Temperatur von mehr als drei Lyam-Grad entspricht ( $$$\ approx (3.2 \ cdot 10 ^ 6) ^ \ circ$ )

Für die Zündung erfordern die Reaktionen normalerweise eine Temperatur in der Größenordnung von 10 ⁸ K , was etwa 320 Hartree entspricht. Lassen Sie uns sehen, in welchen Entfernungen eine ähnliche Energie im Fall des gewöhnlichen Divodoronions und im Fall seiner Myonversion erreicht wird:



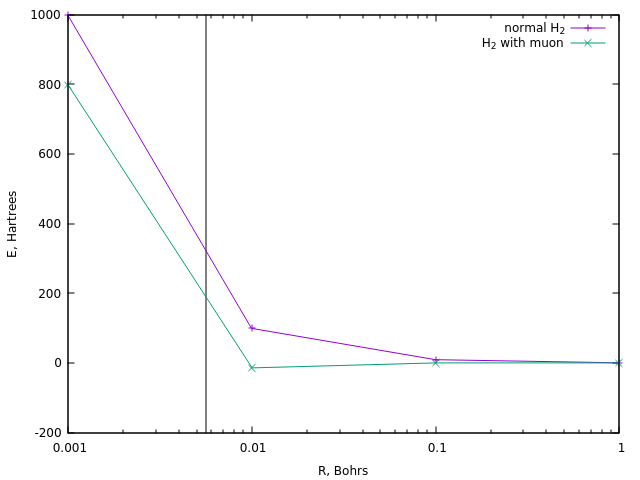
Im ersteren Fall entspricht dies einem Abstand von etwa 0,0058 Bor (vertikale Linie).

Ein ähnlicher Abstand in Myonenwasserstoff wird bei einer Energie von etwa 190 ha erreicht, d.h. ungefähr eineinhalb Mal weniger. Und dies ist die einfachste Schätzung der Temperatur der Myonenkatalyse.

Aber in der Tat wird alles noch cooler. Tatsache ist, dass sich ein stabiles Teilchen bildet $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ dann schwingen diese Kerne, während das Myon lebt, relativ zueinander. Und hier kann ein Tunnel vom Zustand "zwei Wasserstoffatome" in den Zustand "schwererer Kern" auftreten, und die Wahrscheinlichkeit des Tunnelns hängt von der erforderlichen Tunnellänge d ungefähr als ab $$$p ^ {- d}$ Wenn wir die beiden Kerne durch das Myon näher zusammenbringen, erhöhen wir die Wahrscheinlichkeit des Tunnelverlaufs dieser Reaktion erheblich. Leider erfordern Schätzungen dieses Effekts keine Quantenchemie mehr, sondern Kernphysik, so dass dieser Teil der Diskussion den Rahmen dieses Beitrags sprengt. Also werden wir damit aufhören.

PS Warum ist es nicht so einfach?

Tatsächlich ist die Bildung dieser Partikel unter Plasmabedingungen nicht so einfach. Tatsache ist, dass wenn wir zwei Teilchen kollidieren, ihre Gesamtenergie offensichtlich die Dissoziationsenergie (oder Ionisation im Fall eines Kerns + Elektron / Myon) übersteigt. Wenn sie also kollidieren, bilden sie kein stabiles Teilchen (Atom, Ion, Molekül), sondern fliegen vorbei aneinander vorbei. Um aneinander festzuhalten, müssen sie irgendwo überschüssige Energie abwerfen, und dafür brauchen wir ein drittes Extra, das diese Energie aufnimmt. Es kann ein Photon oder eine Art linkes Teilchen sein, das in der Nähe fliegt, aber die Hauptsache ist, dass die Bedingungen zu dieser Mitnahme von überschüssiger Energie beitragen sollten.

PPS

Wenn Sie Kommentare / Erläuterungen / Fragen haben, schreiben Sie in Kommentare oder in PM. Ich werde alles korrigieren, ich werde antworten und alles erklären.