Eintrag
Im
YOW! 2013 einer der Entwickler der Haskell-Sprache,
prof. Philip Wadler zeigte, wie Monaden es reinen Funktionssprachen ermöglichen, im Wesentlichen zwingende Operationen wie Eingabe-Ausgabe und Ausnahmebehandlung auszuführen. Es überrascht nicht, dass das Interesse des Publikums an diesem Thema zu einem explosionsartigen Wachstum der Veröffentlichungen über Monaden im Internet geführt hat. Leider verwenden die meisten dieser Veröffentlichungen Beispiele, die in funktionalen Sprachen geschrieben sind, was bedeutet, dass Neulinge in der funktionalen Programmierung etwas über Monaden lernen möchten. Monaden sind jedoch nicht spezifisch für Haskell oder funktionale Sprachen und können durch Beispiele in imperativen Programmiersprachen veranschaulicht werden. Dies ist der Zweck dieses Handbuchs.
Wie unterscheidet sich dieser Leitfaden von den anderen? Wir werden versuchen, die Monaden in nicht mehr als 15 Minuten zu öffnen, wobei wir nur die Intuition und einige elementare Beispiele für Python-Code verwenden. Daher werden wir nicht anfangen, zu theoretisieren und uns mit Philosophie zu befassen und
Burritos ,
Raumanzüge ,
Schreibtische und Endofunktoren zu diskutieren.
Motivationsbeispiele
Wir werden drei Fragen im Zusammenhang mit der Zusammensetzung von Funktionen betrachten. Wir werden sie auf zwei Arten lösen: den üblichen Imperativ und die Verwendung von Monaden. Dann vergleichen wir die verschiedenen Ansätze.
1. Protokollierung
Angenommen, wir haben drei unäre Funktionen:
f1 ,
f2 und
f3 , die eine Zahl annehmen und diese um 1, 2 bzw. 3 erhöht zurückgeben. Jede Funktion generiert auch eine Nachricht, die einen Bericht über den abgeschlossenen Vorgang darstellt.
def f1(x): return (x + 1, str(x) + "+1") def f2(x): return (x + 2, str(x) + "+2") def f3(x): return (x + 3, str(x) + "+3")
Wir möchten sie verketten, um den Parameter
x , mit anderen Worten, wir möchten
x+1+2+3 berechnen. Darüber hinaus müssen wir eine lesbare Erklärung erhalten, was jede Funktion getan hat.
Wir können das gewünschte Ergebnis auf folgende Weise erzielen:
log = "Ops:" res, log1 = f1(x) log += log1 + ";" res, log2 = f2(res) log += log2 + ";" res, log3 = f3(res) log += log3 + ";" print(res, log)
Diese Lösung ist nicht ideal, da sie aus einer großen Anzahl monotoner Middleware besteht. Wenn wir unserer Kette eine neue Funktion hinzufügen möchten, müssen wir diesen Verknüpfungscode wiederholen. Darüber hinaus beeinträchtigen Manipulationen mit den Variablen
res und
log die Lesbarkeit des Codes, was es schwierig macht, der Hauptlogik des Programms zu folgen.
Idealerweise sollte ein Programm wie eine einfache Funktionskette aussehen, wie
f3(f2(f1(x))) . Leider stimmen die von
f1 und
f2 Datentypen nicht mit den Parametertypen
f2 und
f3 überein. Aber wir können der Kette neue Funktionen hinzufügen:
def unit(x): return (x, "Ops:") def bind(t, f): res = f(t[0]) return (res[0], t[1] + res[1] + ";")
Jetzt können wir das Problem wie folgt lösen:
print(bind(bind(bind(unit(x), f1), f2), f3))
Das folgende Diagramm zeigt den bei
x=0 ablaufenden Rechenprozess. Hier sind
v1 ,
v2 und
v3 die Werte, die als Ergebnis von Aufrufen von
unit und
bind .

Die
unit konvertiert den Eingabeparameter
x in ein Tupel aus einer Zahl und einer Zeichenfolge. Die
bind ruft die an sie übergebene Funktion als Parameter auf und akkumuliert das Ergebnis in der Zwischenvariablen
t .
Wir konnten vermeiden, Middleware zu wiederholen, indem wir sie in die
bind einfügten. Wenn wir nun die Funktion
f4 ,
f4 wir sie einfach in die Kette ein:
bind(f4, bind(f3, ... ))
Und wir müssen keine weiteren Änderungen vornehmen.
2. Liste der Zwischenwerte
Wir werden dieses Beispiel auch mit einfachen unären Funktionen beginnen.
def f1(x): return x + 1 def f2(x): return x + 2 def f3(x): return x + 3
Wie im vorherigen Beispiel müssen wir diese Funktionen zusammensetzen, um
x+1+2+3 zu berechnen. Wir müssen auch eine Liste aller Werte erhalten, die sich aus der Arbeit unserer Funktionen ergeben, dh
x ,
x+1 ,
x+1+2 und
x+1+2+3 .
Im Gegensatz zum vorherigen Beispiel sind unsere Funktionen zusammensetzbar, dh die Typen ihrer Eingabeparameter stimmen mit dem Typ des Ergebnisses überein. Daher gibt eine einfache Kette
f3(f2(f1(x))) das Endergebnis zurück. In diesem Fall verlieren wir jedoch die Zwischenwerte.
Lösen wir das Problem "frontal":
lst = [x] res = f1(x) lst.append(res) res = f2(res) lst.append(res) res = f3(res) lst.append(res) print(res, lst)
Leider enthält diese Lösung auch viel Middleware. Und wenn wir uns entscheiden,
f4 hinzuzufügen, müssen wir diesen Code erneut wiederholen, um die richtige Liste der Zwischenwerte zu erhalten.
Daher fügen wir wie im vorherigen Beispiel zwei zusätzliche Funktionen hinzu:
def unit(x): return (x, [x]) def bind(t, f): res = f(t[0]) return (res, t[1] + [res])
Jetzt schreiben wir das Programm als eine Kette von Aufrufen um:
print(bind(bind(bind(unit(x), f1), f2), f3))
Das folgende Diagramm zeigt den bei
x=0 ablaufenden Rechenprozess. Wiederum bezeichnen
v1 ,
v2 und
v3 die Werte, die von
unit und
bind werden.

3. Leere Werte
Versuchen wir, ein interessanteres Beispiel zu geben, diesmal mit Klassen und Objekten. Angenommen, wir haben eine
Employee Klasse mit zwei Methoden:
class Employee: def get_boss(self):
Jedes Objekt der
Employee Klasse verfügt über einen Manager (ein anderes Objekt der
Employee Klasse) und ein Gehalt, auf die über geeignete Methoden zugegriffen wird. Beide Methoden können auch
None (der Mitarbeiter hat keinen Manager, das Gehalt ist unbekannt).
In diesem Beispiel erstellen wir ein Programm, das das Gehalt des Leiters dieses Mitarbeiters anzeigt. Wenn der Manager nicht gefunden wird oder sein Gehalt nicht ermittelt werden kann, gibt das Programm
None .
Im Idealfall müssen wir so etwas schreiben
print(john.get_boss().get_wage())
In diesem Fall wird unser Programm jedoch mit einem Fehler beendet, wenn eine der Methoden
None zurückgibt.
Ein offensichtlicher Weg, um mit dieser Situation umzugehen, könnte folgendermaßen aussehen:
result = None if john is not None and john.get_boss() is not None and john.get_boss().get_wage() is not None: result = john.get_boss().get_wage() print(result)
In diesem Fall erlauben wir zusätzliche Aufrufe der
get_wage get_boss und
get_wage . Wenn diese Methoden schwer genug sind (z. B. Zugriff auf die Datenbank), reicht unsere Lösung nicht aus. Deshalb ändern wir es:
result = None if john is not None: boss = john.get_boss() if boss is not None: wage = boss.get_wage() if wage is not None: result = wage print(result)
Dieser Code ist hinsichtlich der Berechnung optimal, wird jedoch aufgrund von drei verschachtelten
if schlecht gelesen. Daher werden wir versuchen, den gleichen Trick wie in den vorherigen Beispielen zu verwenden. Definieren Sie zwei Funktionen:
def unit(e): return e def bind(e, f): return None if e is None else f(e)
Und jetzt können wir die gesamte Lösung in einer Zeile zusammenfassen.
print(bind(bind(unit(john), Employee.get_boss), Employee.get_wage))
Wie Sie wahrscheinlich bereits bemerkt haben, mussten wir in diesem Fall die
unit nicht schreiben: Sie gibt einfach den Eingabeparameter zurück. Aber wir werden es so lassen, dass es für uns einfacher ist, unsere Erfahrungen zu verallgemeinern.
Beachten Sie auch, dass wir in Python Methoden als Funktionen verwenden können, mit denen wir
Employee.get_boss(john) anstelle von
john.get_boss() schreiben konnten.
Das folgende Diagramm zeigt den Berechnungsprozess, wenn John keinen Anführer hat, d. H.
john.get_boss() gibt
None .
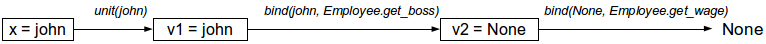
Schlussfolgerungen
Angenommen, wir möchten die Funktionen des gleichen Typs
f1 ,
f2 ,
… ,
fn kombinieren. Wenn ihre Eingabeparameter mit den Ergebnissen übereinstimmen, können wir eine einfache Kette der Form
fn(… f2(f1(x)) …) . Das folgende Diagramm zeigt einen verallgemeinerten Berechnungsprozess mit Zwischenergebnissen, die als
v1 ,
v2 ,
… ,
vn .

Oft ist dieser Ansatz nicht anwendbar. Die Arten von Eingabewerten und Funktionsergebnissen können wie im ersten Beispiel variieren. Oder Funktionen können zusammensetzbar sein, aber wir möchten zusätzliche Logik zwischen Aufrufen einfügen, da wir in den Beispielen 2 und 3 eine Aggregation von Zwischenwerten bzw. eine Prüfung auf einen leeren Wert eingefügt haben.
1. Imperative Entscheidung
In allen Beispielen haben wir zunächst den einfachsten Ansatz verwendet, der durch das folgende Diagramm dargestellt werden kann:

Bevor wir
f1 aufrufen
f1 wir einige Initialisierungen durchgeführt. Im ersten Beispiel haben wir eine Variable zum Speichern eines gemeinsamen Protokolls initialisiert, im zweiten für eine Liste von Zwischenwerten. Danach haben wir Funktionsaufrufe mit einem bestimmten Verbindungscode durchsetzt: Wir haben Aggregatwerte berechnet und das Ergebnis auf
None überprüft.
2. Monaden
Wie wir in den Beispielen gesehen haben, litten imperative Entscheidungen immer unter Ausführlichkeit, Wiederholung und verwirrender Logik. Um eleganteren Code zu erhalten, haben wir ein bestimmtes Entwurfsmuster verwendet, nach dem wir zwei Funktionen erstellt haben:
unit und
bind . Diese Vorlage wird als
Monade bezeichnet . Die
bind enthält Middleware, während das
unit die Initialisierung implementiert. Dies ermöglicht es uns, die endgültige Lösung auf eine Zeile zu vereinfachen:
bind(bind( ... bind(bind(unit(x), f1), f2) ... fn-1), fn)
Der Berechnungsprozess kann durch ein Diagramm dargestellt werden:

Ein Aufruf von
unit(x) erzeugt einen Anfangswert von
v1 . Dann erzeugt
bind(v1, f1) einen neuen Zwischenwert
v2 , der beim nächsten Aufruf zum
bind(v2, f2) . Dieser Prozess wird fortgesetzt, bis ein Endergebnis erhalten wird. Durch die Definition verschiedener
unit und
bind im Rahmen dieser Vorlage können wir verschiedene Funktionen in einer Berechnungskette kombinieren.
Monadenbibliotheken (
z. B. PyMonad oder OSlash, ca. Transl. ) Enthalten normalerweise gebrauchsfertige Monaden (Paare von
unit und
bind ) zum Implementieren bestimmter Funktionszusammensetzungen.
Um Funktionen zu verketten, müssen die von
unit und
bind zurückgegebenen Werte vom gleichen Typ sein wie die Eingabeparameter von
bind . Dieser Typ wird
monadisch genannt . In Bezug auf das obige Diagramm muss der Typ der Variablen
v1 ,
v2 ,
… ,
vn ein monadischer Typ sein.
Überlegen Sie abschließend, wie Sie den mit Monaden geschriebenen Code verbessern können. Offensichtlich wirken wiederholte
bind unelegant. Um dies zu vermeiden, definieren Sie eine andere externe Funktion:
def pipeline(e, *functions): for f in functions: e = bind(e, f) return e
Jetzt stattdessen
bind(bind(bind(bind(unit(x), f1), f2), f3), f4)
Wir können die folgende Abkürzung verwenden:
pipeline(unit(x), f1, f2, f3, f4)
Fazit
Monaden sind ein einfaches und leistungsstarkes Entwurfsmuster, mit dem Funktionen erstellt werden. In deklarativen Programmiersprachen hilft es, zwingende Mechanismen wie Protokollierung oder Eingabe / Ausgabe zu implementieren. In imperativen Sprachen
Es hilft, Code zu verallgemeinern und zu verkürzen, der eine Reihe von Aufrufen von Funktionen desselben Typs verknüpft.
Dieser Artikel bietet nur ein oberflächliches, intuitives Verständnis von Monaden. Weitere Informationen erhalten Sie bei folgenden Quellen:
- Wikipedia
- Monaden in Python (mit schöner Syntax!)
- Zeitleiste der Monaden-Tutorials