Arten von Unendlichkeiten und Hirnstamm

Dieser Artikel ist eine Fortsetzung eines Artikels über große Zahlen . Aber jetzt werden wir noch weiter gehen - in die Unendlichkeit der Unendlichkeit.

Dafür brauchen wir ZFC - die Mengenlehre Zermelo, Frenkel + Choice. Wahl ist das Axiom der Wahl, das umstrittenste Axiom der Mengenlehre. Sie verdient einen separaten Artikel. Es wird davon ausgegangen, dass Sie die "Kraft" des Sets kennen. Wenn nicht, dann google, sicher wird dies besser angegeben als ich. Hier werde ich nur einige erinnern

Bekannte Fakten

• Die Potenz einer Menge von ganzen Zahlen wird mit bezeichnet $$ . Dies ist die erste unendliche Kraft, solche Mengen werden als zählbar bezeichnet.
• Die Potenz einer unendlichen Teilmenge von ganzen Zahlen ist einfach, gerade usw. - auch zählbar.
• Die Menge der rationalen Zahlen, dh die Brüche p / q, ist ebenfalls zählbar, sie können von einer Schlange weitergegeben werden.
• Für jede Stromversorgung gibt es eine Powerset-Operation - die Menge aller Teilmengen, die mehr Strom erzeugt als die ursprüngliche. Manchmal wird diese Operation als Erhöhen einer Zwei auf eine Potenz bezeichnet, d.h. $$ . Potenzsatz aus der berechneten Leistung ist die Leistung des Kontinuums.
• Kontinuumskraft besitzt: endliche und unendliche Segmente, planare und volumetrische Figuren und sogar n-dimensionale Räume als Ganzes
• Für gewöhnliche Mathematik gilt folgende Kraft: $$ Praktisch nicht erforderlich, normalerweise erfolgt die gesamte Arbeit mit zählbaren Sätzen und Kontinuumsleistungssätzen

Jetzt

Wenig bekannte Fakten

In ZFC können nicht alle Elementauflistungen festgelegt werden. Es gibt Sammlungen, die so breit sind, dass es unmöglich ist, sie als Mengen zuzulassen, Paradoxe entstehen. Insbesondere ist die " Menge aller Mengen " keine Menge. Es gibt jedoch Mengen-Theorien, in denen solche Mengen erlaubt sind.

Weiter. Mengenlehre ... Welche Objekte? Zahlen? Ein Apfel? Orangen? Seltsamerweise benötigt ZFC keine Objekte. Nehmen Sie die leere Menge {} und stimmen Sie zu, dass sie 0 bedeutet. 1 bezeichnet mit {{}} die Zwei als {{{}}} und so weiter. {5,2} ist {{{{{{{}}}}}, {{{}}}. Mit ganzen Zahlen können wir reale erstellen, und Sammlungen von realen können beliebige Formen erstellen.

Die Mengenlehre ist also ... wie man sagt ... eine hohle Theorie. Diese Theorie handelt von nichts. Genauer gesagt, wie Sie Klammern verschachteln (nisten, dh ineinander setzen) können.

Die einzige in der Mengenlehre definierte Operation ist $$ - ein Symbol der Zugehörigkeit. Aber was ist mit Vereinigung, Ausgrenzung, Gleichheit usw.? Dies sind alles Makros, zum Beispiel:

$$

Das heißt, bei der Übersetzung ins Russische werden zwei Mengen als gleich angesehen, wenn beim Testen eines Elements auf Zugehörigkeit zu ihnen die gleichen Ergebnisse erzielt werden

Die Mengen sind nicht geordnet, aber dies kann behoben werden: Das geordnete Paar (p, v) sei {{p}, {p, v}}. Aus Sicht des Programmierers unelegant, aber genug für einen Mathematiker. Jetzt setzt die Menge aller Parameter-Wert-Paare eine Funktion, die nun auch gesetzt ist! Et voila! Alle mathematischen Analysen, die auf der Ebene der Sprachen zweiter Ordnung funktionieren, da sie nicht von der Existenz von Zahlen , sondern von der Existenz von Funktionen sprechen, kollabieren zu einer Sprache erster Ordnung!

Die Mengenlehre ist also eine schlechte Theorie ohne Objekte und mit einem Beziehungssymbol, das absolut monströse Kraft besitzt - ohne neue Annahmen erzeugt sie aus sich selbst formale Arithmetik, reelle Zahlen, Analyse, Geometrie und vieles mehr. Dies ist eine Art TOE-Mathematik.

Kontinuumshypothese - CH

Gibt es Macht zwischen $$ und $$ ? Cantor konnte dieses Problem nicht lösen, der „König der Mathematiker“ Hilbert lobte seine Bedeutung, aber erst später wurde bewiesen, dass diese Hypothese weder bewiesen noch widerlegt werden kann. Sie ist unabhängig von ZFC.

Dies bedeutet, dass Sie zwei verschiedene Mathematikarten erstellen können: eine mit ZFC + CH, die andere mit ZFC + (nicht CH). In der Tat sogar mehr als zwei. Angenommen, wir lehnen CH ab, das heißt, wir werden das zwischen glauben $$ und $$ Es gibt immer noch Macht. Wie viele kann es geben? Eins, zwei? Gödel glaubte, dass nur einer. Wie sich jedoch herausstellte, führt die Annahme, dass es 2, 17, 19393493 gibt, nicht zu Widersprüchen. Beliebige Zahl, aber nicht unendlich!

Wenn wir in der formalen Arithmetik auf eine unbeweisbare Aussage stoßen, wissen wir aus bestimmten Gründen, dass diese Aussage, obwohl sie nicht beweisbar ist, tatsächlich entweder wahr oder falsch ist. In der Mengenlehre funktioniert das nicht, wir bekommen wirklich verschiedene Mathematiker. Wie soll man damit umgehen? Es gibt drei philosophische Ansätze:

Formalismus: Warum eigentlich überrascht sein? Wir legen die Regeln des Symbolspiels fest, verschiedene Regeln - ein anderes Ergebnis. Sie müssen nicht nach einem Problem suchen, bei dem es nicht vorhanden ist

Platonismus: Aber wie kann man dann erklären, dass völlig unterschiedliche Theorien wie ZFC und New Foundations, die auf völlig unterschiedlichen Prinzipien beruhen, fast immer das gleiche Ergebnis liefern? Bedeutet dies, dass hinter den Formeln eine Art Realität steckt, die wir studieren? Diese Ansicht wurde zum Beispiel von Gödel vertreten

Multiversum: Wir können viele Axiomaten haben, die manchmal das gleiche Ergebnis liefern, manchmal nicht. Wir müssen das Bild als Ganzes wahrnehmen - wenn Farbe mit verschiedenen Axiomensystemen assoziiert ist, dann ist der farbige Effektbaum Mathematik. Wenn etwas überall wahr ist - es ist weiß, aber es gibt auch farbige Zweige.

Höher und höher.

In Zukunft werden wir der Einfachheit halber die Kontinuumshypothese akzeptieren, d.h. $$ - es ist sehr bequem. Tatsächlich werden wir auch das stärkere Axiom akzeptieren, die verallgemeinerte Kontinuumshypothese, dass es zwischen x und Powerset (x) niemals Zwischenkräfte gibt. Jetzt iterieren wir das Powerset und alles ist einfach:

$$

Wie weit können wir gehen? Nach einer unendlichen Anzahl von Iterationen kommen wir zu $$ - unendliche Kraft in Ordnung! Übrigens war seine Existenz für Cantor nicht offensichtlich. Aber eine Sekunde! Schließlich ist die Powerset-Funktion daher immer definiert $$ kann nicht der letzte sein!

$$

Um zu bekommen $$ Es ist notwendig, das Powerset unendlich und noch dreimal zu wiederholen. Haben Sie bereits begonnen, das Dach abzureißen? Sonst wird es sein. Denn wieder, nachdem wir das Powerset unendlich oft wiederholt haben, kommen wir zu $$ , danach natürlich $$

Nachdem wir unendlich oft die Unendlichkeit erreicht haben , erhalten wir den Index $$ . Wie gefällt Ihnen diese Kraft zum Beispiel: $$ ? Während wir das Powerset über die Liste der Ordnungszahlen iterierten, sind hier die ersten Ordnungszahlen:



aber es gibt viele, viele mehr. Also werden wir alles sofort überspringen und es tun

Großer Schritt sofort

Achtung! Was unten geschrieben steht, kann für Ihr Gehirn gefährlich sein! Wir haben das Powerset zählbar oft wiederholt, aber winken wir nicht dem Kontinuum zu ? Ehrlich gesagt bin ich selbst ein bisschen Wurst von der Tatsache, dass der Zyklus ein Kontinuum von Zeiten durchgeführt werden kann, aber die Mengenlehre erfordert Existenz

$$

Als nächstes werden wir schneller gehen:

$$

Der letzte Alef hat einen Index von Null, aber der lokale Latex erlaubt es nicht, ihn zu setzen - es gibt zu viele Ebenen. Aber die Hauptsache ist, dass Sie verstanden haben, egal wie neue monströse Kraft wir erschaffen würden, wir können sagen - ja, dies ist nur ein Repeater , und diese ganze Konstruktion in Form eines Index für das neue Aleph setzen. Jetzt wachsen die Kapazitäten wie ein Schneeball, wir können nicht aufgehalten werden, die Pyramide der Alephs ist höher und wir können jede Kraft erzeugen ... Oder nicht?

Unerreichbare Kraft

Was ist, wenn die Kraft so groß ist? $$ dass wir es nicht erreichen werden, egal wie wir versuchen, es „von unten“ zu erreichen, indem wir Strukturen aus Alephs bauen? Es stellt sich heraus, dass die Existenz einer solchen Macht unabhängig von ZFC ist. Sie können seine Existenz akzeptieren oder nicht.

Ich höre das Flüstern von Occams Rasiermesser ... Nein, nein. Mathematiker halten sich an das entgegengesetzte Prinzip, das als ontologischer Maximalismus bezeichnet wird - lassen Sie alles Mögliche existieren. Es gibt jedoch noch mindestens zwei weitere Gründe, warum ich diese Hypothese akzeptieren möchte.

• Erstens ist dies nicht die erste unerreichbare Kraft, die wir kennen. Erstens ... das ist die bekannte Zählkraft. Seltsamerweise sind alle Eigenschaften unerreichbar - es ist einfach nicht üblich, es so zu nennen:
• Es gibt keine Möglichkeit, unendliche Potenz „von unten“ zu erhalten - weder das endliche Hinzufügen von Elementen noch das endliche Iterieren von Powerset () mit endlichen Mengen für Seed erhalten Sie keine Unendlichkeit. Um unendlich zu werden, müssen Sie es bereits irgendwo haben.
• Die Existenz unendlicher Kraft wird durch ein spezielles Axiom eingeführt - das Axiom der Unendlichkeit. Ohne sie ist die Existenz unendlicher Macht nicht beweisbar.

Zweitens: Wenn wir das Axiom der Unendlichkeit ablehnen, erhalten wir FinSet, eine einfache Spielzeugsatztheorie mit endlichen Mengen. Schreiben wir alle diese Mengen auf (das sogenannte Theoriemodell ).

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

Und wir bekommen ... eine unendliche Menge endlicher Mengen ... Das heißt, das Modell der Theorie der endlichen Mengen ist unendlich und spielt die Rolle der "Menge aller Mengen" darin. Vielleicht hilft dies zu verstehen, warum die Theorie nicht über die „Menge aller Mengen“ sprechen kann - eine solche Menge existiert immer als Modell außerhalb der Theorie und hat andere Eigenschaften als Mengen innerhalb. Sie können das Unendliche nicht zur Theorie der endlichen Mengen hinzufügen.

Und ja $$ es ist die "Menge aller Mengen" der ZFC-Theorie. In diesem Video wird am Ende sehr schön über unerreichbare Kraft gesagt, aber wir müssen weitermachen.

Noch weiter.

Natürlich können wir durch Iteration noch weiter gehen $$ . Nachdem wir alle oben beschriebenen Schritte durchlaufen haben und riesige Repeater-Türme gebaut haben, stoßen wir erneut auf einen unerreichbaren Kardinal (aber jetzt brauchen wir keine neuen Axiome, mit dem Axiom der Existenz unerreichbarer Kraft, das wir gerade hinzugefügt haben, ist dies beweisbar geworden). Und immer wieder.

$$

Beachten Sie, dass der Pfeil für uns jetzt nicht mehr so ​​sinnvoll ist wie die Ausführung der Powerset () - Funktion, sondern GetNextInaccessible (). Ansonsten sieht alles sehr ähnlich aus, wir haben:

$$

Dann werden wir definitiv etwas erreichen ... oder nicht?

Hierarchie großer Kapazitäten.

Ja, mit GetNextInaccessible stoßen wir auf eine unerreichbare Leistung. Seine Existenz erfordert ein weiteres Axiom. Es gibt hyper-hyper-unerreichbare Kräfte. Usw. Es gibt aber auch andere Möglichkeiten, die Macht zu bestimmen , nicht nur durch Unerreichbarkeit:



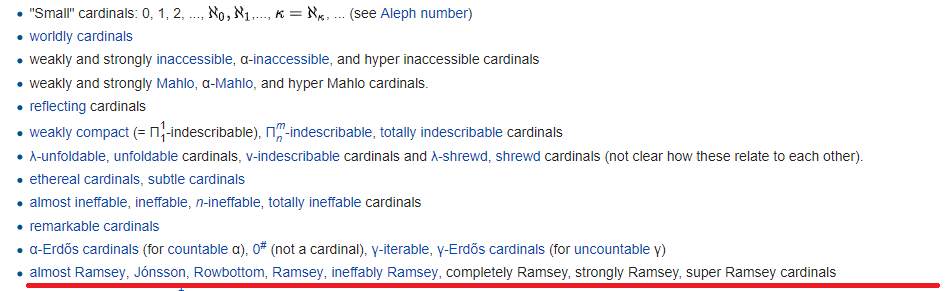
Hinter jedem Link befindet sich in der Regel eine endlose Hierarchie mit einer beliebigen Anzahl von Hyper- und Repeater-Präfixen. Die Gesamtzahl der Formeln, die unerreichbare Kardinäle bestimmen, ist jedoch nicht so groß - denn die Anzahl der Formeln ist zählbar !!! Daher werden sie früher oder später enden. Wo sie enden, wird eine rote Linie gezogen. Alles unter dieser Linie ist unsicherer definiert, wenn auch formal.

Die rote Linie selbst markiert das Ende von Gödels Universum (aber vergessen Sie nicht, dass Gödel ZWEI verschiedene Universen erschaffen hat) - das Universum von Mengen, die mit Formeln von unten konstruiert wurden. Kapazitäten oberhalb der roten Linie werden als hmm, "klein" und darunter - groß bezeichnet:



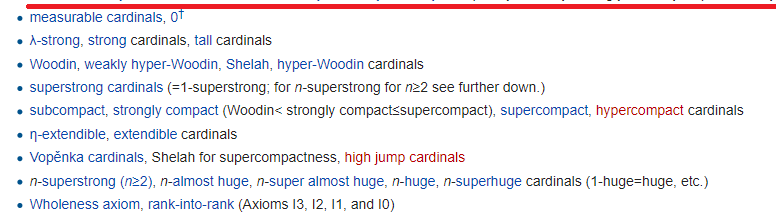
Die Hauptidee in ihnen ist, dass das Universum der Mengen so groß wird, dass es beginnt, sich in verschiedenen Sinnen zu wiederholen. Jede Zeile erfordert wie immer ein separates Axiom und mehrere. Und was noch interessanter ist, all dies ist nicht so nutzlos, wie Sie vielleicht denken. Zum Beispiel wird das stärkste Axiom (Rang-in-Rang) ganz unten benötigt , um die Tatsache über die Tabletten zu beweisen .

Unten ist eine Umfrage, die letzte Auswahl wird hier entschlüsselt.