Nein, natürlich meine ich es nicht ernst. Es muss eine Grenze geben, inwieweit es möglich ist, das Thema zu vereinfachen. Für die ersten Phasen, ein Verständnis der Grundkonzepte und einen schnellen "Einstieg" in das Thema kann dies jedoch zulässig sein. Und wie man dieses Material richtig benennt (Optionen: „Maschinelles Lernen für Dummies“, „Analyse der Daten aus den Windeln“, „Algorithmen für die Kleinsten“), werden wir am Ende diskutieren.
Zum Geschäft. Er schrieb mehrere Anwendungsprogramme auf MS Excel zur Visualisierung und Visualisierung von Prozessen, die bei der Analyse von Daten in verschiedenen Methoden des maschinellen Lernens ablaufen. Sehen ist letztendlich Glauben nach den Medien der Kultur, die die meisten dieser Methoden entwickelt haben (übrigens keineswegs alle. Die leistungsstärkste "Support Vector Method" oder SVM, Support Vector Machine, ist eine Erfindung unseres Landsmanns Vladimir Vapnik, Moskauer Institut für Management. 1963 übrigens! Jetzt lehrt und arbeitet er jedoch in den USA.
Drei Dateien zur Überprüfung
1. K-bedeutet Clustering
Aufgaben dieser Art beziehen sich auf „Lernen ohne Lehrer“. Wenn wir die Anfangsdaten in eine bestimmte Anzahl von Kategorien aufteilen müssen, die im Voraus bekannt sind, aber keine „richtigen Antworten“ haben, müssen wir sie aus den Daten selbst extrahieren. Das grundlegende klassische Problem, Unterarten von Irisblüten zu finden (Ronald Fisher, 1936!), Das als erstes Zeichen dieses Wissensgebiets gilt, ist von solcher Natur.
Die Methode ist recht einfach. Wir haben eine Menge von Objekten, die als Vektoren dargestellt werden (Mengen von N Zahlen). Bei Iris handelt es sich um Sätze von 4 Zahlen, die eine Blume charakterisieren: die Länge und Breite der äußeren bzw. inneren Blütenhüllen (
Iris Fisher - Wikipedia ). Als Abstand oder Maß für die Nähe zwischen Objekten wird die übliche kartesische Metrik gewählt.
Ferner werden die Zentren der Cluster willkürlich ausgewählt (oder nicht willkürlich, siehe unten), und die Abstände von jedem Objekt zu den Zentren der Cluster werden berechnet. Jedes Objekt in diesem Iterationsschritt wird als zum nächsten Zentrum gehörend markiert. Dann wird der Mittelpunkt jedes Clusters auf das arithmetische Mittel der Koordinaten seiner Mitglieder übertragen (analog zur Physik wird er auch als "Massenschwerpunkt" bezeichnet), und der Vorgang wird wiederholt.
Der Prozess konvergiert schnell genug. In den zweidimensionalen Bildern sieht es so aus:
1. Die anfängliche zufällige Verteilung der Punkte in der Ebene und die Anzahl der Cluster

2. Definieren Sie die Clusterzentren und weisen Sie ihren Clustern Punkte zu
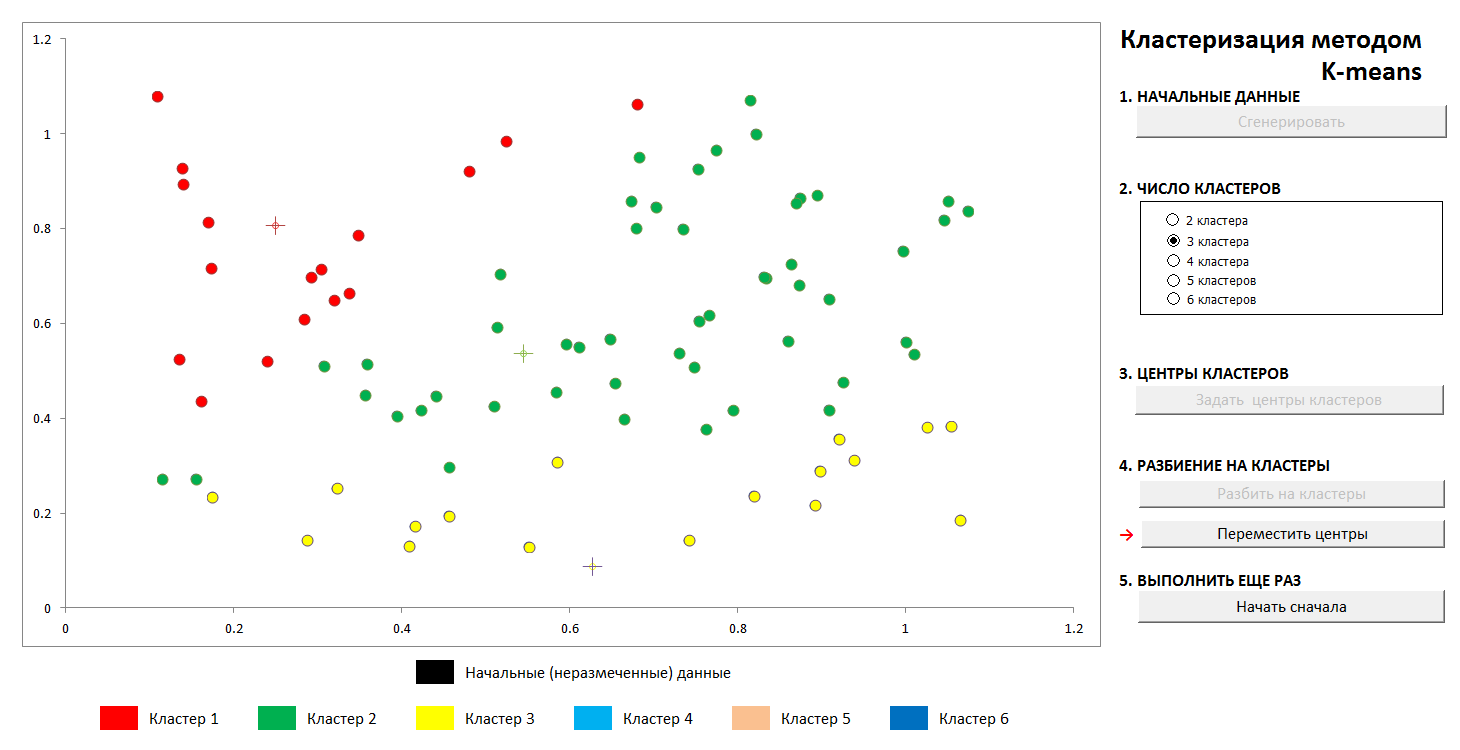
3. Übertragung der Koordinaten der Clusterzentren, Neuberechnung der Punkte, bis sich die Zentren stabilisiert haben. Die Flugbahn von der Mitte des Clusters zur Endposition ist sichtbar.

Sie können jederzeit neue Cluster-Center festlegen (ohne eine neue Punkteverteilung zu generieren!) Und feststellen, dass der Partitionierungsprozess nicht immer eindeutig ist. Mathematisch bedeutet dies, dass wir für die optimierte Funktion (die Summe der Quadrate der Abstände von den Punkten zu den Zentren ihrer Cluster) kein globales, sondern ein lokales Minimum finden. Dieses Problem kann entweder durch eine nicht zufällige Auswahl der Anfangszentren der Cluster oder durch Aussortieren der möglichen Zentren behoben werden (manchmal ist es vorteilhaft, sie genau an einem bestimmten Punkt zu platzieren, dann besteht zumindest die Garantie, dass wir keine leeren Cluster erhalten). In jedem Fall hat eine endliche Menge immer eine exakte Untergrenze.
Sie können mit dieser Datei unter diesem Link spielen (vergessen Sie nicht, die Makrounterstützung zu aktivieren. Dateien werden auf Viren überprüft).
Beschreibung der Wikipedia-Methode -
k-means-Methode2. Approximation durch Polynome und Datenaufschlüsselung. Umschulung
Ein bemerkenswerter Wissenschaftler und Popularisierer der Datenwissenschaft K.V. Woronzow spricht kurz über Methoden des maschinellen Lernens als "die Wissenschaft des Zeichnens von Kurven durch Punkte". In diesem Beispiel finden wir das Muster in den Daten nach der Methode der kleinsten Quadrate.
Die Technik der Aufteilung der Quelldaten in "Training" und "Kontrolle" sowie ein Phänomen wie Umschulung oder "Umschulung" für die Daten wird gezeigt. Mit der richtigen Näherung haben wir einen bestimmten Fehler in den Trainingsdaten und einen etwas größeren Fehler in den Kontrolldaten. Wenn es falsch ist, ist es eine genaue Anpassung der Trainingsdaten und ein großer Fehler bei der Steuerung.
(Es ist eine bekannte Tatsache, dass es durch N Punkte möglich ist, eine einzelne Kurve des N-1. Grades zu zeichnen, und diese Methode liefert im Allgemeinen nicht das gewünschte Ergebnis. Das
Lagrange-Interpolationspolynom auf Wikipedia )
1. Wir legen die anfängliche Verteilung fest

2. Teilen Sie die Punkte im Verhältnis 70 zu 30 in „Training“ und „Kontrolle“ ein.

3. Wir zeichnen eine Näherungskurve für die Trainingspunkte, wir sehen den Fehler, den es auf den Kontrolldaten gibt

4. Wir zeichnen die genaue Kurve durch die Trainingspunkte und sehen einen ungeheuren Fehler in den Kontrolldaten (und Null im Training, aber worum geht es?).

Natürlich wird die einfachste Variante mit einer einzelnen Aufteilung in Teilmengen "Training" und "Kontrolle" gezeigt, im allgemeinen Fall wird dies wiederholt durchgeführt, um die Koeffizienten bestmöglich anzupassen.
Die Datei ist hier verfügbar, Antivirus geprüft. Aktivieren Sie die Makros, um ordnungsgemäß zu funktionieren
3. Gradientenabstieg und Fehlerdynamik
Es wird einen 4-dimensionalen Fall und eine lineare Regression geben. Die linearen Regressionskoeffizienten werden schrittweise durch das Gradientenabstiegsverfahren bestimmt, anfangs sind alle Koeffizienten Nullen. Ein separates Diagramm zeigt die Dynamik der Fehlerreduzierung, da die Koeffizienten immer feiner abgestimmt werden. Es ist möglich, alle vier zweidimensionalen Projektionen zu sehen.
Wenn Sie den Gradientenabstiegsschritt zu groß einstellen, ist es klar, dass jedes Mal, wenn wir das Minimum überspringen, das Ergebnis in einer größeren Anzahl von Schritten erreicht wird, obwohl wir am Ende trotzdem kommen werden (es sei denn, wir berühren den Abstiegsschritt zu stark, dann geht der Algorithmus “ im Abstand "). Und der Graph der Abhängigkeit des Fehlers vom Iterationsschritt ist nicht glatt, sondern "ruckartig".
1. Generieren Sie Daten und legen Sie den Gradientenabstiegsschritt fest
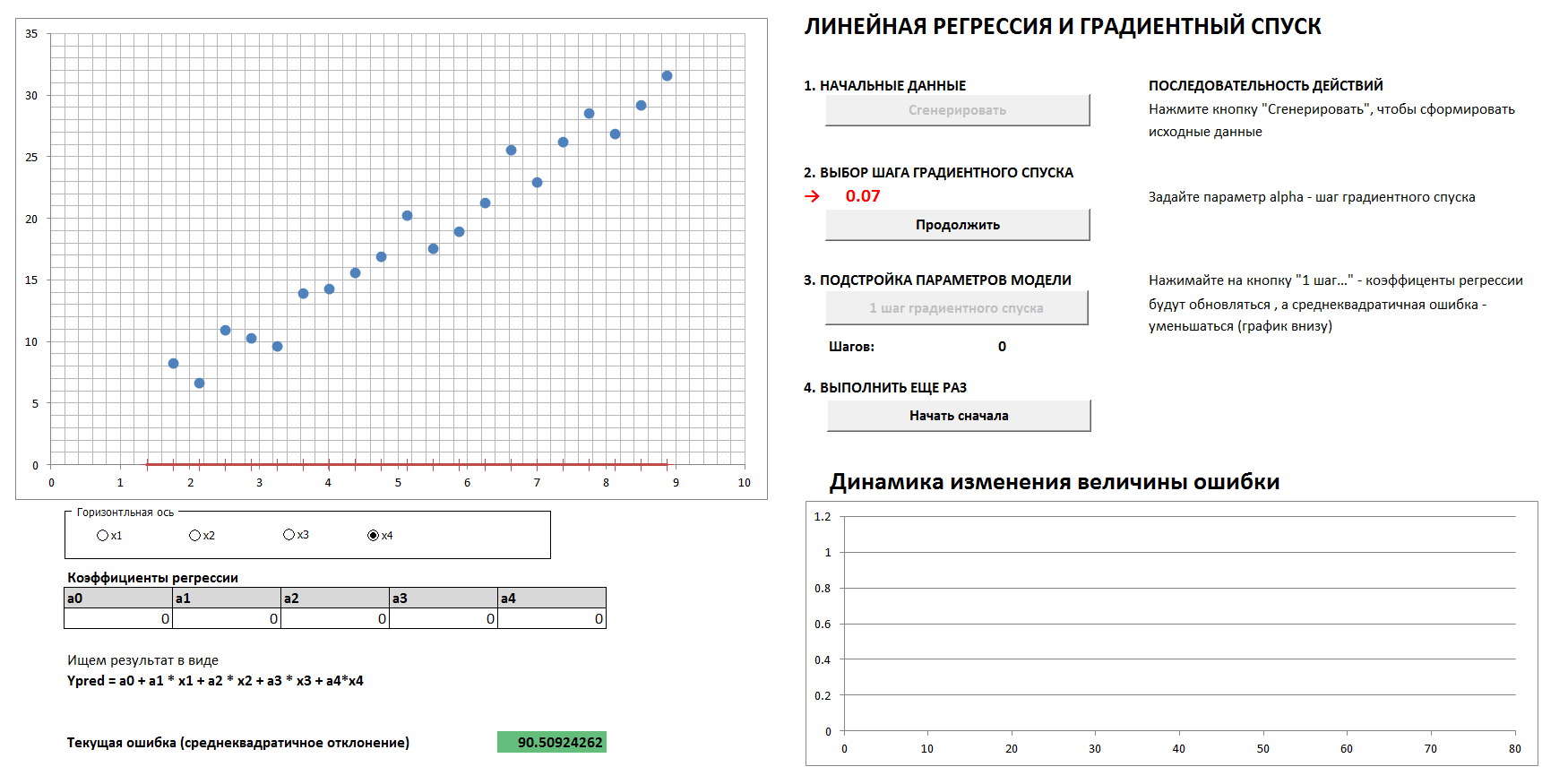
2. Mit der richtigen Wahl des Gradientenabstiegs kommen wir reibungslos und schnell genug auf ein Minimum

3. Wenn der Schritt des Gradientenabfalls falsch ausgewählt ist, überspringen wir das Maximum, das Fehlerdiagramm ist "ruckartig", die Konvergenz dauert eine größere Anzahl von Schritten

und

4. Bei einer völlig falschen Auswahl des Gradientenabstiegsschritts entfernen wir uns vom Minimum

(Um den Vorgang mit den in den Bildern gezeigten Werten des Gradientenabstiegsschritts zu reproduzieren, aktivieren Sie das Kontrollkästchen "Referenzdaten".)
Datei - über diesen Link müssen Sie Makros aktivieren, es gibt keine Viren.Ist eine solche Vereinfachung und Präsentationsmethode nach Ansicht einer angesehenen Community akzeptabel? Soll ich den Artikel ins Englische übersetzen?