"An was für einen Teufel sollte ich mich auswendig an all diese verdammten Algorithmen und Datenstrukturen erinnern?"
Diesbezüglich kommt es auf die Kommentare der meisten Artikel zum Durchgang technischer Interviews an. Die Hauptthese lautet in der Regel, dass alles, was auf die eine oder andere Weise verwendet wird, bereits zehnmal implementiert wurde und es höchst unwahrscheinlich ist, dass sich dieser gewöhnliche Programmierer damit befassen muss. Nun, bis zu einem gewissen Grad ist dies wahr. Aber wie sich herausstellte, wurde nicht alles implementiert, und ich musste leider (oder zum Glück?) Immer noch eine Datenstruktur erstellen.
Geheimnisvolle modifizierte Merkle Patricia Trie.
Da es zu diesem Baum überhaupt keine Informationen über den Habr und das Medium gibt - ein bisschen mehr - möchte ich Ihnen sagen, um welche Art von Tier es sich handelt und womit es gefressen wird.

Was ist das?
Haftungsausschluss: Die Hauptinformationsquelle für die Implementierung war für mich das Gelbe Papier sowie die Quellcodes Parity-Ethereum und Go-Ethereum . Es gab ein Minimum an theoretischen Informationen zur Rechtfertigung bestimmter Entscheidungen, daher sind alle Schlussfolgerungen über die Gründe für bestimmte Entscheidungen meine persönlichen. Falls ich mich in etwas irre - ich freue mich über Korrekturen in den Kommentaren.
Ein Baum ist eine Datenstruktur, die ein zusammenhängender azyklischer Graph ist. Hier ist alles einfach, das kennt jeder.
Der Präfixbaum ist der Stammbaum, in dem Schlüssel-Wert-Paare gespeichert werden können, da die Knoten in zwei Typen unterteilt sind: diejenigen, die einen Teil des Pfads (Präfix) enthalten, und Blattknoten, die den gespeicherten Wert enthalten. Ein Wert ist in einem Baum genau dann vorhanden, wenn wir mit dem Schlüssel den ganzen Weg von der Wurzel des Baums gehen und einen Knoten mit einem Wert am Ende finden können.
Der PATRICIA-Baum ist ein Präfixbaum, in dem die Präfixe binär sind - das heißt, jeder Schlüsselknoten speichert Informationen über ein Bit.
Der Merkle- Baum ist ein Hash-Baum, der auf einer Art Datenkette aufgebaut ist und dieselben Hashes zu einem (Root) zusammenfasst und Informationen über den Status aller Datenblöcke speichert. Das heißt, der Root-Hash ist eine Art "digitale Signatur" des Zustands der Blockkette. Dieses Ding wird aktiv in der Blockchain verwendet, und mehr darüber finden Sie hier .

Gesamt: Modifizierte Merkle Patricia Trie (im Folgenden kurz MPT) ist ein Hash-Baum, in dem Schlüssel-Wert-Paare gespeichert werden, während die Schlüssel in binärer Form dargestellt werden. Und worum es genau bei „Modified“ geht, erfahren wir etwas später, wenn wir die Implementierung besprechen.
Warum ist das so?
MPT wird im Ethereum-Projekt verwendet, um Daten über Konten, Transaktionen, Ergebnisse ihrer Ausführung und andere Daten zu speichern, die für das Funktionieren des Systems erforderlich sind.
Im Gegensatz zu Bitcoin, bei dem der Status implizit ist und von jedem Knoten unabhängig berechnet wird, wird der Kontostand jedes Kontos (sowie die damit verbundenen Daten) direkt in der Blockchain in der Luft gespeichert. Darüber hinaus sollte das Auffinden und die Invarianz von Daten kryptografisch bereitgestellt werden - nur wenige Personen verwenden Kryptowährung, bei der sich der Kontostand eines zufälligen Kontos ohne objektive Gründe ändern kann.
Das Hauptproblem der Entwickler von Ethereum ist die Erstellung einer Datenstruktur, mit der Sie Schlüssel-Wert-Paare effektiv speichern und gleichzeitig die gespeicherten Daten überprüfen können. Also erschien MPT.
Wie ist es?
MPT ist ein Präfix-PATRICIA-Baum, in dem die Schlüssel Folgen von Bytes sind.
Die Kanten in diesem Baum sind Halbbyte-Sequenzen (halbe Bytes). Dementsprechend kann ein Knoten bis zu 16 Nachkommen haben (entsprechend Zweigen von 0x0 bis 0xF).
Knoten sind in 3 Typen unterteilt:
- Zweigknoten. Der zum Verzweigen verwendete Knoten. Enthält bis zu 1 bis 16 Links zu untergeordneten Knoten. Kann auch einen Wert enthalten.
- Erweiterungsknoten. Ein Hilfsknoten, der einen Teil des Pfads speichert, der mehreren untergeordneten Knoten gemeinsam ist, sowie eine Verknüpfung zum Zweigknoten, der darunter liegt.
- Blattknoten. Ein Knoten, der einen Teil des Pfads und einen gespeicherten Wert enthält. Es ist das Ende in der Kette.
Wie bereits erwähnt, basiert MPT auf einem anderen kv-Repository, in dem Knoten in Form von "link" => " RLP codierter Knoten" gespeichert werden.
Und hier haben wir ein neues Konzept: RLP. Kurz gesagt, dies ist eine Methode zum Codieren von Daten, die Listen oder Bytesequenzen darstellen. Beispiel: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . Ich werde nicht besonders auf Details eingehen, und bei der Implementierung verwende ich eine vorgefertigte Bibliothek, da auch die Berichterstattung über dieses Thema einen bereits ziemlich großen Artikel aufblähen wird. Wenn Sie noch interessiert sind, können Sie hier mehr lesen. Wir beschränken uns auf die Tatsache, dass wir Daten in RLP codieren und zurückdecodieren können.
Eine Verbindung zu einem Knoten ist wie folgt definiert: Wenn die Länge des RLP codierten Knotens 32 oder mehr Bytes beträgt, ist die Verbindung ein keccak Hash aus der RLP Darstellung des Knotens. Wenn die Länge weniger als 32 Bytes beträgt, ist die Verbindung die RLP Darstellung des Knotens selbst.
Im zweiten Fall müssen Sie den Knoten natürlich nicht in der Datenbank speichern, weil Es wird vollständig im übergeordneten Knoten gespeichert.

Die Kombination von drei Knotentypen ermöglicht es Ihnen, Daten effektiv zu speichern, wenn nur wenige Schlüssel vorhanden sind (dann werden die meisten Pfade in Erweiterungs- und Blattknoten gespeichert und es gibt nur wenige Verzweigungsknoten) und wenn viele Knoten vorhanden sind (Pfade werden nicht explizit gespeichert). aber sie "sammeln" sich während des Durchgangs durch Zweigknoten).
Ein vollständiges Beispiel eines Baums mit allen Arten von Knoten:
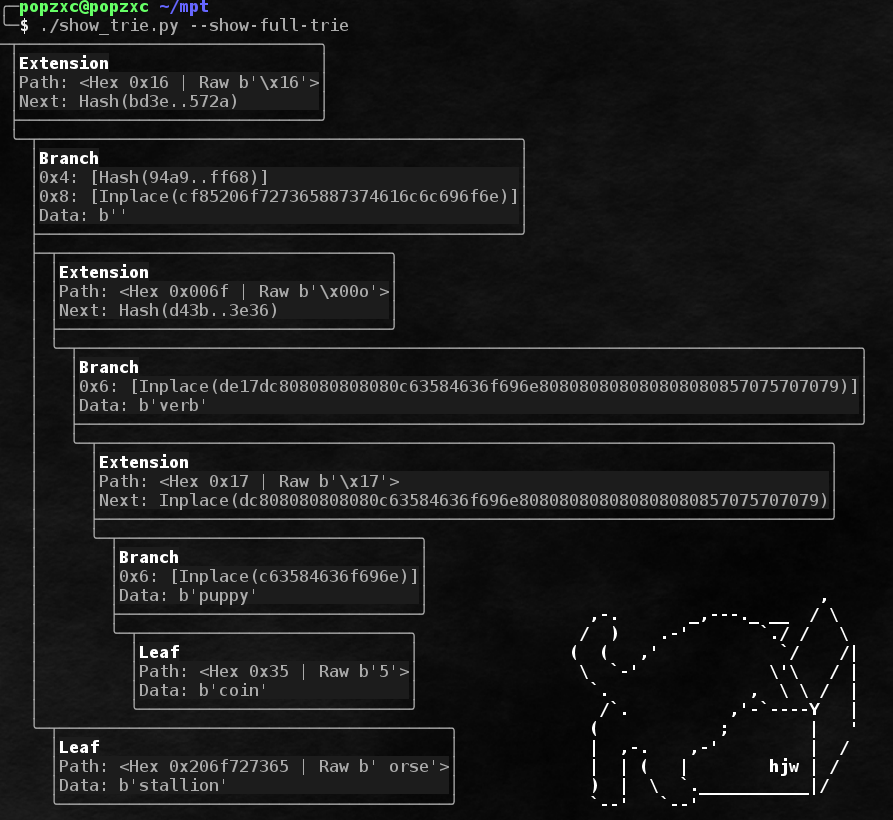
Wie Sie vielleicht bemerkt haben, haben die gespeicherten Teile der Pfade Präfixe. Präfixe werden für verschiedene Zwecke benötigt:
- Unterscheidungsknoten von Blattknoten unterscheiden.
- Zum Ausrichten von Sequenzen einer ungeraden Anzahl von Knabbereien.
Die Regeln zum Erstellen von Präfixen sind sehr einfach:
- Das Präfix benötigt 1 Nibble. Wenn die Pfadlänge (ohne das Präfix) ungerade ist, beginnt der Pfad unmittelbar nach dem Präfix. Wenn die Pfadlänge gerade ist, wird zum Ausrichten nach dem Präfix zuerst Nibble 0x0 hinzugefügt.
- Das Präfix ist anfänglich 0x0.
- Wenn die Pfadlänge ungerade ist, wird 0x1 zum Präfix hinzugefügt, wenn gerade - 0x0.
- Wenn der Pfad zu einem Blattknoten führt, wird 0x2 zum Präfix hinzugefügt, wenn 0x0 zum Erweiterungsknoten hinzugefügt wird.
Bei Beatiks wird es meiner Meinung nach klarer:
0b0000 => , Extension 0b0001 => , Extension 0b0010 => , Leaf 0b0011 => , Leaf
Entfernung, die keine Entfernung ist
Trotz der Tatsache, dass der Baum Knoten löscht, bleibt alles, was einmal hinzugefügt wurde, für immer im Baum.
Dies ist erforderlich, um nicht für jeden Block einen vollständigen Baum zu erstellen, sondern nur den Unterschied zwischen der alten und der neuen Version des Baums zu speichern.
Dementsprechend können wir unter Verwendung verschiedener Root-Hashes als Einstiegspunkt jeden der Zustände abrufen, in denen sich der Baum jemals befunden hat.

Dies sind nicht alle Optimierungen. Es gibt noch mehr, aber wir werden nicht darüber sprechen - und so ist der Artikel groß. Sie können jedoch selbst lesen .
Implementierung
Die Theorie ist vorbei, lasst uns zur Praxis übergehen. Wir werden Verkehrssprache aus der IT-Welt verwenden, das ist python .
Da es viel Code geben wird und für das Format des Artikels viel reduziert und geteilt werden muss, werde ich sofort einen Link zu github hinterlassen .
Bei Bedarf sehen Sie dort das ganze Bild.
Zunächst definieren wir die Baumschnittstelle, die wir als Ergebnis erhalten möchten:
class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
Die Schnittstelle ist sehr einfach. Verfügbare Vorgänge sind das Abrufen, Löschen, Einfügen und Ändern (kombiniert im Update) sowie das Abrufen des Root-Hash.
Der Speicher wird an die Methode __init__ - eine __init__ Datenstruktur, in der wir die Knoten sowie root speichern - die "Spitze" des Baums. Wenn None als root , gehen wir davon aus, dass der Baum leer ist und von Grund auf neu funktioniert.
_Remark: Sie fragen sich möglicherweise, warum die Variablen in den Methoden als encoded_key und encoded_value und nicht nur als key / value . Die Antwort ist einfach: Gemäß der Spezifikation müssen alle Schlüssel und Werte in RLP codiert sein. Wir werden uns damit keine Sorgen machen und diesen Beruf den Bibliotheksbenutzern überlassen.
Bevor wir jedoch mit der Implementierung des Baums selbst beginnen, müssen zwei wichtige Dinge getan werden:
- Implementieren Sie die
NibblePath Klasse, eine Kette von Nibbles, um sie nicht manuell zu codieren. - So implementieren Sie die
Node Klasse im Rahmen dieser Klasse - Extension , Leaf und Branch .
Knabberweg
Also, NibblePath . Da wir uns aktiv im Baum bewegen, sollte die Grundlage für die Funktionalität unserer Klasse die Fähigkeit sein, den "Versatz" vom Anfang des Pfades an festzulegen und ein bestimmtes Knabbern zu erhalten. In diesem Wissen definieren wir die Basis unserer Klasse (sowie einige nützliche Konstanten für die Arbeit mit den folgenden Präfixen):
class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data
Ganz einfach, nicht wahr?
Es bleiben nur Funktionen zum Codieren und Decodieren einer Folge von Halbbytes zu schreiben.
class NibblePath:
Im Prinzip ist dies das Minimum, das für ein bequemes Arbeiten mit Knabbereien erforderlich ist. Natürlich gibt es in der aktuellen Implementierung noch eine Reihe von Hilfsmethoden (z. B. combine , Zusammenführen von zwei Pfaden zu einem), aber ihre Implementierung ist sehr trivial. Bei Interesse finden Sie die Vollversion hier .
Knoten
Wie wir bereits wissen, sind unsere Knoten in drei Typen unterteilt: Blatt, Erweiterung und Zweig. Alle können codiert und decodiert werden, und der einzige Unterschied besteht in den darin gespeicherten Daten. Um ehrlich zu sein, sind dies algebraische Datentypen, und in Rust würde ich zum Beispiel etwas im Geiste schreiben:
pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), }
In Python als solchem gibt es jedoch kein ADT. Daher definieren wir die Node Klasse. Darin befinden sich drei Klassen, die den Knotentypen entsprechen. Wir implementieren die Codierung direkt in den Knotenklassen und die Decodierung in der Node .
Die Implementierung ist jedoch elementar:
Blatt:
class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self):
Erweiterung:
class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self):
Zweig:
class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self):
Alles ist sehr einfach. Das einzige, was Fragen verursachen kann, ist die Funktion _prepare_reference_for_encoding .
Dann gestehe ich, ich musste eine kleine Krücke benutzen. Tatsache ist, dass die verwendete rlp Bibliothek die Daten rekursiv decodiert und die Verknüpfung zu einem anderen Knoten, wie wir wissen, rlp Daten sein kann (falls der codierte Knoten weniger als 32 Zeichen lang ist). Das Arbeiten mit Links in zwei Formaten - Hash-Bytes und einem dekodierten Knoten - ist sehr unpraktisch. Aus diesem Grund habe ich zwei Funktionen geschrieben, die nach dem Dekodieren des Knotens die Links im Byte-Format zurückgeben und gegebenenfalls vor dem Speichern dekodieren. Diese Funktionen sind:
def _prepare_reference_for_encoding(ref):
Beenden Sie mit Knoten, indem Sie eine Node schreiben. Es gibt nur zwei Methoden: Dekodieren Sie den Knoten und verwandeln Sie den Knoten in eine Verknüpfung.
class Node:
Eine Pause
Fuh! Es gibt viele Informationen. Ich denke es ist Zeit sich zu entspannen. Hier ist eine weitere Katze für dich:
Milota, richtig? Okay, zurück zu unseren Bäumen.
MerklePatriciaTrie
Hurra - Hilfselemente sind fertig, wir gehen zu den leckersten über. Für alle Fälle erinnere ich die Benutzeroberfläche an unseren Baum. Gleichzeitig implementieren wir die Methode __init__ .
class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
Aber mit den restlichen Methoden werden wir uns eins nach dem anderen befassen.
bekommen
Die get Methode (wie im Prinzip die anderen Methoden) besteht aus zwei Teilen. Die Methode selbst bereitet die Daten vor und bringt das Ergebnis in die erwartete Form, während die eigentliche Arbeit innerhalb der Hilfsmethode erfolgt.
Die grundlegende Methode ist sehr einfach:
class MerklePatriciaTrie:
_get nicht viel komplizierter: Um zum gewünschten Knoten zu gelangen, müssen wir vom Stamm zum gesamten bereitgestellten Pfad wechseln. Wenn wir am Ende einen Knoten mit Daten gefunden haben (Blatt oder Zweig) - Hurra, werden die Daten empfangen. Wenn das Bestehen nicht möglich war, fehlt der erforderliche Schlüssel im Baum.
Implementierung:
class MerklePatriciaTrie:
Gleichzeitig werden wir Methoden zum Speichern und Laden von Knoten schreiben. Sie sind einfach:
class MerklePatriciaTrie:
Update
Die update Methode ist bereits interessanter. Gehen Sie einfach bis zum Ende durch und fügen Sie den Blattknoten ein, der nicht immer funktioniert. Es ist wahrscheinlich, dass sich der Schlüsseltrennpunkt irgendwo innerhalb des bereits gespeicherten Blatt- oder Erweiterungsknotens befindet. In diesem Fall müssen Sie sie trennen und mehrere neue Knoten erstellen.
Im Allgemeinen kann jede Logik durch die folgenden Regeln beschrieben werden:
- Während der Pfad vollständig mit den vorhandenen Knoten übereinstimmt, steigen wir den Baum rekursiv ab.
- Wenn der Pfad fertig ist und wir uns im Zweig- oder Blattknoten befinden, bedeutet dies, dass durch
update einfach der Wert aktualisiert wird, der diesem Schlüssel entspricht. - Wenn die Pfade geteilt sind (dh wir aktualisieren den Wert nicht, sondern fügen einen neuen ein), befinden wir uns im Zweigknoten. Erstellen Sie einen Blattknoten und geben Sie im entsprechenden Zweigzweig einen Link dazu an.
- Wenn die Pfade geteilt sind und wir uns im Blatt- oder Erweiterungsknoten befinden, müssen wir einen Verzweigungsknoten erstellen, der die Pfade trennt, und gegebenenfalls einen Erweiterungsknoten für den gemeinsamen Teil des Pfads.
Lassen Sie uns dies schrittweise im Code ausdrücken. Warum nach und nach? Weil die Methode groß ist und es schwierig sein wird, sie in großen Mengen zu verstehen.
Ich werde hier jedoch einen Link zur vollständigen Methode hinterlassen.
class MerklePatriciaTrie:
Es gibt nicht genug allgemeine Logik, das Interessanteste ist drinnen, if s.
if type(node) == Node.Leaf
Lassen Sie uns zunächst die Blattknoten behandeln. Mit ihnen sind nur 2 Szenarien möglich:
Der Rest des Pfades, dem wir folgen, entspricht genau dem Pfad, der im Blattknoten gespeichert ist. In diesem Fall müssen wir nur den Wert ändern, den neuen Knoten speichern und einen Link dazu zurückgeben.
Die Wege sind unterschiedlich.
In diesem Fall müssen Sie einen Verzweigungsknoten erstellen, der die beiden Pfade trennt.
Wenn einer der Pfade leer ist, wird sein Wert direkt an den Verzweigungsknoten übertragen.
Andernfalls müssen zwei Blattknoten erstellt werden, die um die Länge des gemeinsamen Teils der Pfade + 1 Halbbyte verkürzt sind (dieses Halbbyte wird durch den Index des entsprechenden Zweigs des Zweigknotens angezeigt).
Sie müssen auch überprüfen, ob es einen gemeinsamen Teil des Pfads gibt, um zu verstehen, ob wir auch einen Erweiterungsknoten erstellen müssen.
Im Code sieht es folgendermaßen aus:
if type(node) == Node.Leaf: if node.path == path:
Die Prozedur _create_branch_node lautet wie folgt:
def _create_branch_node(self, path_a, value_a, path_b, value_b):
if type(node) == Node.Extension
Im Fall des Erweiterungsknotens sieht alles wie ein Blattknoten aus.
Wenn der Pfad vom Erweiterungsknoten ein Präfix für unseren Pfad ist, fahren wir einfach rekursiv fort.
Andernfalls müssen wir die Trennung mithilfe des Verzweigungsknotens durchführen, wie im oben beschriebenen Fall.
Dementsprechend ist der Code:
elif type(node) == Node.Extension: if path.starts_with(node.path):
Die Prozedur _create_branch_extension entspricht logisch der Prozedur _create_branch_leaf , funktioniert jedoch mit dem Erweiterungsknoten.
if type(node) == Node.Branch
Aber mit dem Branch-Node ist alles einfach. Wenn der Pfad leer ist, speichern wir einfach den neuen Wert im aktuellen Zweigknoten. Wenn der Pfad nicht leer ist, „beißen“ wir ein Knabbern davon ab und gehen rekursiv tiefer.
Ich denke, der Code braucht keine Kommentare.
elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node)
löschen
Fuh! Die letzte Methode bleibt bestehen. Er ist der fröhlichste. Die Komplexität des Löschens besteht darin, dass wir die Struktur in den Zustand zurückversetzen müssen, in den sie gefallen wäre, wenn wir die gesamte update ohne den gelöschten Schlüssel durchgeführt hätten.
, , , , . "", , .
. , N- , N+1 . enum — DeleteAction , .
delete :
class MerklePatriciaTrie:
, get update . . .
if type(node) == Node.Leaf
. . — , , .
:
if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError
, "" — . , . .
if type(node) == Node.Extension
C Extension- :
- , Extension- . — .
_delete , "" .- . :
- . .
- . .
- Branch-. . , Branch- . , , Leaf-. — Extension-.
:
elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError
if type(node) == Node.Branch
.
, . Branch-, …
Warum? Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .
? :
:
- , .
- ,
_delete .
:
elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else:
_DeleteAction .
- Branch- , ( , ). .
if action == MerklePatriciaTrie._DeleteAction.UPDATED:
- ( , ), , .
. :
- . , , , . , .
- , . Leaf- . .
- , . , , .
- , , Branch- . ,
_DeleteAction — UPDATED .
if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0:
_build_new_node_from_last_branch .
— Leaf Extension, , .
— Branch, Extension , , Branch.
def _build_new_node_from_last_branch(self, branches):
Der Rest
. , … root .
Hier:
class MerklePatriciaTrie:
, .
… . , , Ethereum . , , , . , :)
, , pip install -U eth_mpt — .

Ergebnisse
?
, -, , - , , . — , .
-, , , — . , skip list interval tree, — , , .
-, , . , - .
-, — .
, , — !
: 1 , 2 , 3 . ! , .