Wir haben bereits die PostgreSQL- Indizierungs-Engine , die Schnittstelle der Zugriffsmethoden und drei Methoden besprochen: Hash-Index , B-Tree und GiST . In diesem Artikel beschreiben wir SP-GiST.

SP-GiST

Zunächst ein paar Worte zu diesem Namen. Der Teil "GiST" spielt auf eine gewisse Ähnlichkeit mit der gleichnamigen Zugriffsmethode an. Die Ähnlichkeit besteht: Beide sind verallgemeinerte Suchbäume, die einen Rahmen für die Erstellung verschiedener Zugriffsmethoden bieten.

"SP" steht für Space Partitioning. Der Raum hier ist oft genau das, was wir als Raum bezeichnen, zum Beispiel eine zweidimensionale Ebene. Aber wir werden sehen, dass jeder Suchraum gemeint ist, dh tatsächlich jede Wertdomäne.

SP-GiST eignet sich für Strukturen, bei denen der Raum rekursiv in nicht schneidende Bereiche aufgeteilt werden kann. Diese Klasse umfasst Quadtrees, k-dimensionale Bäume (kD-Bäume) und Radix-Bäume.

Struktur

Die Idee der SP-GiST-Zugriffsmethode besteht also darin, die Wertdomäne in nicht überlappende Subdomänen aufzuteilen, von denen jede wiederum auch aufgeteilt werden kann. Eine solche Partitionierung führt zu nicht ausgeglichenen Bäumen (im Gegensatz zu B-Bäumen und regulären GiST).

Die Eigenschaft, sich nicht zu überschneiden, vereinfacht die Entscheidungsfindung beim Einfügen und Suchen. Andererseits sind die induzierten Bäume in der Regel schwach verzweigt. Beispielsweise hat ein Knoten eines Quadtree normalerweise vier untergeordnete Knoten (im Gegensatz zu B-Bäumen, bei denen die Knoten Hunderte betragen) und eine größere Tiefe. Bäume wie diese passen gut zur Arbeit im RAM, aber der Index wird auf einer Festplatte gespeichert. Um die Anzahl der E / A-Vorgänge zu verringern, müssen Knoten in Seiten gepackt werden, und dies ist nicht einfach effizient durchzuführen. Außerdem kann die Zeit, die benötigt wird, um verschiedene Werte im Index zu finden, aufgrund von Unterschieden in den Verzweigungstiefen variieren.

Diese Zugriffsmethode übernimmt wie GiST Aufgaben auf niedriger Ebene (gleichzeitiger Zugriff und Sperren, Protokollierung und ein reiner Suchalgorithmus) und bietet eine spezielle vereinfachte Schnittstelle, um die Unterstützung neuer Datentypen und neuer Partitionierungsalgorithmen zu ermöglichen.

Ein interner Knoten des SP-GiST-Baums speichert Verweise auf untergeordnete Knoten. Für jede Referenz kann ein Etikett definiert werden. Außerdem kann ein interner Knoten einen Wert speichern, der als Präfix bezeichnet wird . Tatsächlich ist dieser Wert kein obligatorisches Präfix; Es kann als beliebiges Prädikat betrachtet werden, das für alle untergeordneten Knoten erfüllt ist.

Blattknoten von SP-GiST enthalten einen Wert vom indizierten Typ und einen Verweis auf eine Tabellenzeile (TID). Die indizierten Daten selbst (Suchschlüssel) können als Wert verwendet werden, sind jedoch nicht obligatorisch: Ein verkürzter Wert kann gespeichert werden.

Darüber hinaus können Blattknoten in Listen gruppiert werden. Ein interner Knoten kann also nicht nur auf einen Wert verweisen, sondern auf eine ganze Liste.

Beachten Sie, dass Präfixe, Beschriftungen und Werte in Blattknoten unabhängig voneinander ihre eigenen Datentypen haben.

Wie in GiST ist die Konsistenzfunktion die Hauptfunktion, die für die Suche definiert werden muss . Diese Funktion wird für einen Baumknoten aufgerufen und gibt eine Reihe von untergeordneten Knoten zurück, deren Werte mit dem Suchprädikat "übereinstimmen" (wie üblich in der Form " Operatorausdruck für indizierte Felder "). Für einen Blattknoten bestimmt die Konsistenzfunktion, ob der indizierte Wert in diesem Knoten dem Suchprädikat entspricht.

Die Suche beginnt mit dem Wurzelknoten. Mit der Konsistenzfunktion können Sie herausfinden, welche untergeordneten Knoten ein Besuch sinnvoll ist. Der Algorithmus wiederholt sich für jeden der gefundenen Knoten. Die Suche steht an erster Stelle.

Auf der physischen Ebene werden Indexknoten in Seiten gepackt, um die Arbeit mit den Knoten unter dem Gesichtspunkt von E / A-Operationen effizient zu gestalten. Beachten Sie, dass eine Seite entweder interne oder Blattknoten enthalten kann, jedoch nicht beide.

Beispiel: Quadtree

Ein Quadtree wird verwendet, um Punkte in einer Ebene zu indizieren. Eine Idee ist, Bereiche rekursiv in vier Teile (Quadranten) in Bezug auf den Mittelpunkt aufzuteilen. Die Tiefe der Zweige in einem solchen Baum kann variieren und hängt von der Dichte der Punkte in geeigneten Quadranten ab.

So sieht es in Zahlen aus, am Beispiel der Demo-Datenbank, die von Flughäfen auf der Website openflights.org erweitert wurde . Übrigens haben wir kürzlich eine neue Version der Datenbank veröffentlicht, in der wir unter anderem Längen- und Breitengrad durch ein Feld vom Typ "Punkt" ersetzt haben.


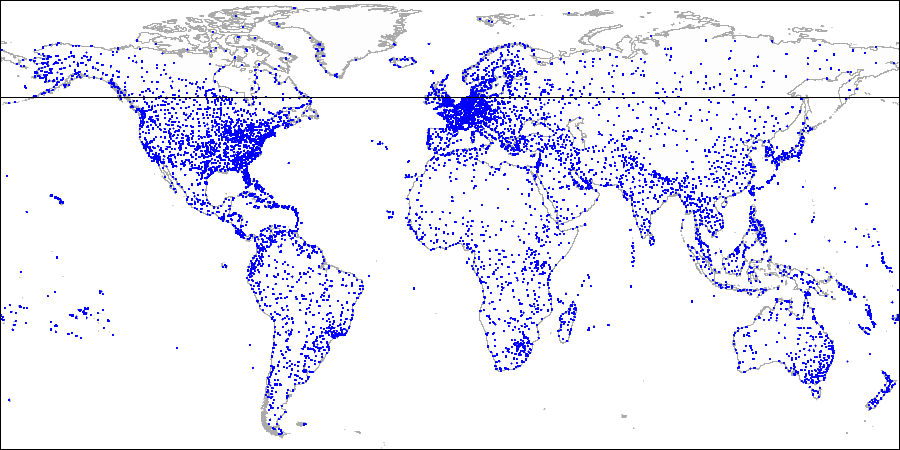
Zuerst teilen wir das Flugzeug in vier Quadranten auf ...


Dann teilen wir jeden der Quadranten ...


Und so weiter, bis wir die endgültige Partitionierung erhalten.

Lassen Sie uns weitere Details eines einfachen Beispiels bereitstellen, das wir bereits im GiST-Artikel betrachtet haben . Sehen Sie, wie die Partitionierung in diesem Fall aussehen könnte:



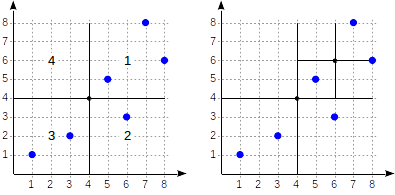
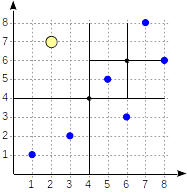
Die Quadranten sind wie in der ersten Abbildung gezeigt nummeriert. Platzieren wir die untergeordneten Knoten aus Gründen der Bestimmtheit genau in derselben Reihenfolge von links nach rechts. Eine mögliche Indexstruktur in diesem Fall ist in der folgenden Abbildung dargestellt. Jeder interne Knoten verweist auf maximal vier untergeordnete Knoten. Jede Referenz kann wie in der Abbildung mit der Quadrantennummer gekennzeichnet werden. Die Implementierung enthält jedoch keine Bezeichnung, da es bequemer ist, ein festes Array von vier Referenzen zu speichern, von denen einige leer sein können.



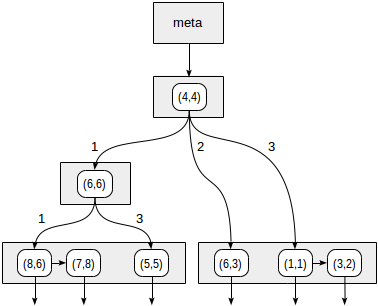
Punkte, die an den Grenzen liegen, beziehen sich auf den Quadranten mit der kleineren Zahl.

postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index points_quad_idx on points using spgist(p); 

In diesem Fall wird standardmäßig die Operatorklasse "quad_point_ops" verwendet, die die folgenden Operatoren enthält:

 postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'quad_point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amopstrategy -----------------+-------------- <<(point,point) | 1 strictly left >>(point,point) | 5 strictly right ~=(point,point) | 6 coincides <^(point,point) | 10 strictly below >^(point,point) | 11 strictly above <@(point,box) | 8 contained in rectangle (6 rows) 

Schauen wir uns zum Beispiel an, wie die Abfrage select * from points where p >^ point '(2,7)' wird (finden Sie alle Punkte, die über dem angegebenen liegen).



Wir beginnen mit dem Wurzelknoten und verwenden die Konsistenzfunktion, um auszuwählen, zu welchen untergeordneten Knoten abzusteigen ist. Für den Operator >^ vergleicht diese Funktion den Punkt (2,7) mit dem Mittelpunkt des Knotens (4,4) und wählt die Quadranten aus, die die gesuchten Punkte enthalten können, in diesem Fall den ersten und vierten Quadranten.

In dem Knoten, der dem ersten Quadranten entspricht, bestimmen wir erneut die untergeordneten Knoten unter Verwendung der Konsistenzfunktion. Der zentrale Punkt ist (6,6), und wir müssen noch einmal durch den ersten und vierten Quadranten schauen.



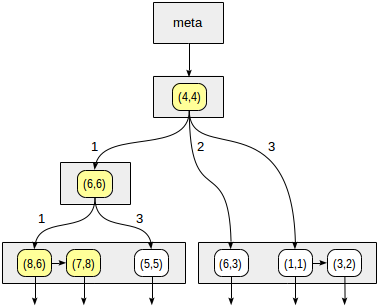
Die Liste der Blattknoten (8.6) und (7.8) entspricht dem ersten Quadranten, von dem nur der Punkt (7.8) die Abfragebedingung erfüllt. Der Verweis auf den vierten Quadranten ist leer.

Im internen Knoten (4.4) ist auch der Verweis auf den vierten Quadranten leer, wodurch die Suche abgeschlossen wird.

 postgres=# set enable_seqscan = off; postgres=# explain (costs off) select * from points where p >^ point '(2,7)'; 

  QUERY PLAN ------------------------------------------------ Index Only Scan using points_quad_idx on points Index Cond: (p >^ '(2,7)'::point) (2 rows) 

Interna

Wir können die interne Struktur von SP-GiST-Indizes mithilfe der bereits erwähnten Erweiterung " gevel " untersuchen. Schlechte Nachrichten sind, dass diese Erweiterung aufgrund eines Fehlers mit modernen Versionen von PostgreSQL nicht richtig funktioniert. Eine gute Nachricht ist, dass wir planen, "pageinspect" mit der Funktionalität von "gevel" ( Diskussion ) zu erweitern. Und der Fehler wurde bereits in "pageinspect" behoben.

Wiederum ist eine schlechte Nachricht, dass der Patch ohne Fortschritt hängen geblieben ist.

Nehmen wir zum Beispiel die erweiterte Demo-Datenbank, mit der Bilder mit der Weltkarte gezeichnet wurden.

 demo=# create index airports_coordinates_quad_idx on airports_ml using spgist(coordinates); 

Zunächst können wir einige Statistiken für den Index erhalten:

 demo=# select * from spgist_stats('airports_coordinates_quad_idx'); 

  spgist_stats ---------------------------------- totalPages: 33 + deletedPages: 0 + innerPages: 3 + leafPages: 30 + emptyPages: 2 + usedSpace: 201.53 kbytes+ usedInnerSpace: 2.17 kbytes + usedLeafSpace: 199.36 kbytes+ freeSpace: 61.44 kbytes + fillRatio: 76.64% + leafTuples: 5993 + innerTuples: 37 + innerAllTheSame: 0 + leafPlaceholders: 725 + innerPlaceholders: 0 + leafRedirects: 0 + innerRedirects: 0 (1 row) 

Und zweitens können wir den Indexbaum selbst ausgeben:

 demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_quad_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix point, -- prefix type node_label int, -- label type (unused here) leaf_value point -- list value type ) order by tid, n; 

  tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------------+------------------ (1,1) | 0 | 1 | (5,3) | (-10.220,53.588) | (1,1) | 1 | 1 | (5,2) | (-10.220,53.588) | (1,1) | 2 | 1 | (5,1) | (-10.220,53.588) | (1,1) | 3 | 1 | (5,14) | (-10.220,53.588) | (3,68) | | 3 | | | (86.107,55.270) (3,70) | | 3 | | | (129.771,62.093) (3,85) | | 4 | | | (57.684,-20.430) (3,122) | | 4 | | | (107.438,51.808) (3,154) | | 3 | | | (-51.678,64.191) (5,1) | 0 | 2 | (24,27) | (-88.680,48.638) | (5,1) | 1 | 2 | (5,7) | (-88.680,48.638) | ... 

Beachten Sie jedoch, dass „spgist_print“ nicht alle Blattwerte ausgibt, sondern nur den ersten aus der Liste und daher eher die Struktur des Index als dessen vollständigen Inhalt anzeigt.

Beispiel: k-dimensionale Bäume

Für die gleichen Punkte in der Ebene können wir auch eine andere Möglichkeit vorschlagen, den Raum zu unterteilen.

Zeichnen wir eine horizontale Linie durch den ersten indizierten Punkt. Es teilt die Ebene in zwei Teile: obere und untere. Der zweite zu indizierende Punkt fällt in einen dieser Teile. Zeichnen wir durch diesen Punkt eine vertikale Linie , die diesen Teil in zwei Teile aufteilt: rechts und links. Wir ziehen wieder eine horizontale Linie durch den nächsten Punkt und eine vertikale Linie durch den nächsten Punkt und so weiter.

Alle auf diese Weise erstellten internen Knoten des Baums haben nur zwei untergeordnete Knoten. Jede der beiden Referenzen kann entweder zum nächsten internen Knoten in der Hierarchie oder zur Liste der Blattknoten führen.

Diese Methode kann leicht für k-dimensionale Räume verallgemeinert werden, und daher werden die Bäume in der Literatur auch als k-dimensionale (kD-Bäume) bezeichnet.

Erläuterung der Methode am Beispiel von Flughäfen:


Zuerst teilen wir das Flugzeug in obere und untere Teile ...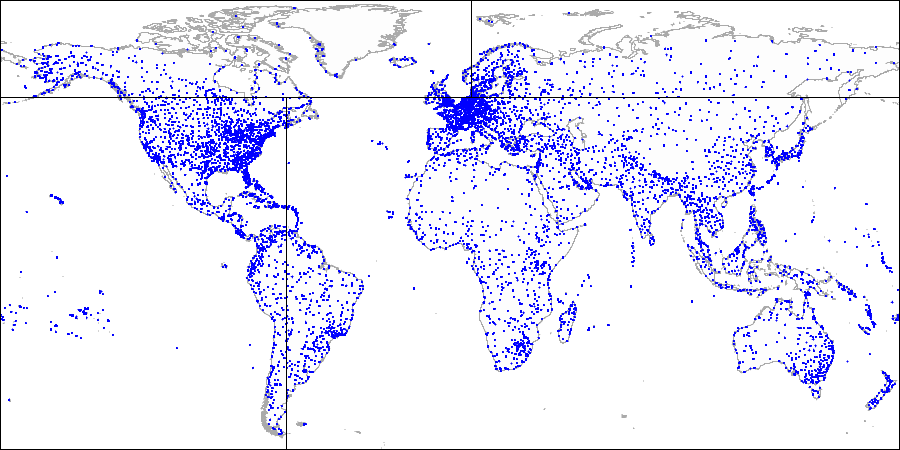


Dann teilen wir jedes Teil in linke und rechte Teile ...


Und so weiter, bis wir die endgültige Partitionierung erhalten.

Um eine Partitionierung wie diese zu verwenden, müssen Sie beim Erstellen eines Index die Operatorklasse "kd_point_ops" explizit angeben.

 postgres=# create index points_kd_idx on points using spgist(p kd_point_ops); 

Diese Klasse enthält genau die gleichen Operatoren wie die "Standard" -Klasse "quad_point_ops".

Interna

Wenn wir durch die Baumstruktur schauen, müssen wir berücksichtigen, dass das Präfix in diesem Fall nur eine Koordinate und kein Punkt ist:

 demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_kd_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix float, -- prefix type node_label int, -- label type (unused here) leaf_value point -- list node type ) order by tid, n; 

  tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------+------------------ (1,1) | 0 | 1 | (5,1) | 53.740 | (1,1) | 1 | 1 | (5,4) | 53.740 | (3,113) | | 6 | | | (-7.277,62.064) (3,114) | | 6 | | | (-85.033,73.006) (5,1) | 0 | 2 | (5,12) | -65.449 | (5,1) | 1 | 2 | (5,2) | -65.449 | (5,2) | 0 | 3 | (5,6) | 35.624 | (5,2) | 1 | 3 | (5,3) | 35.624 | ... 

Beispiel: Radixbaum

Wir können SP-GiST auch verwenden, um einen Radix-Baum für Zeichenfolgen zu implementieren. Die Idee eines Radixbaums besteht darin, dass eine zu indizierende Zeichenfolge nicht vollständig in einem Blattknoten gespeichert wird, sondern durch Verketten der in den darüber liegenden Knoten gespeicherten Werte bis zur Wurzel erhalten wird.

Angenommen, wir müssen die URLs der Site indizieren: "postgrespro.ru", "postgrespro.com", "postgresql.org" und "planet.postgresql.org".

 postgres=# create table sites(url text); postgres=# insert into sites values ('postgrespro.ru'),('postgrespro.com'),('postgresql.org'),('planet.postgresql.org'); postgres=# create index on sites using spgist(url); 

Der Baum sieht wie folgt aus:



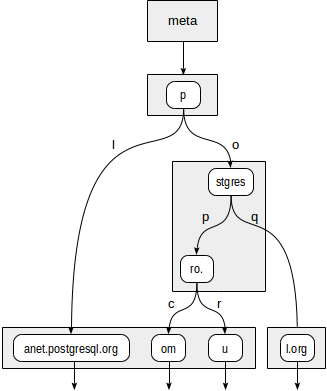
Die internen Knoten des Baums speichern Präfixe, die allen untergeordneten Knoten gemeinsam sind. In untergeordneten Knoten von "stgres" beginnen die Werte beispielsweise mit "p" + "o" + "stgres".

Im Gegensatz zu Quadtrees ist jeder Zeiger auf einen untergeordneten Knoten zusätzlich mit einem Zeichen gekennzeichnet (genauer gesagt mit zwei Bytes, dies ist jedoch nicht so wichtig).

Die Operatorklasse "Text_ops" unterstützt B-Baum-ähnliche Operatoren: "gleich", "größer" und "kleiner":

 postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'text_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amopstrategy -----------------+-------------- ~<~(text,text) | 1 ~<=~(text,text) | 2 =(text,text) | 3 ~>=~(text,text) | 4 ~>~(text,text) | 5 <(text,text) | 11 <=(text,text) | 12 >=(text,text) | 14 >(text,text) | 15 (9 rows) 

Der Unterschied zwischen Operatoren mit Tildes besteht darin, dass sie eher Bytes als Zeichen bearbeiten.

Manchmal kann sich eine Darstellung in Form eines Radixbaums als viel kompakter als ein B-Baum herausstellen, da die Werte nicht vollständig gespeichert, sondern bei Bedarf beim Abstieg durch den Baum rekonstruiert werden.

Betrachten Sie eine Abfrage: select * from sites where url like 'postgresp%ru' . Es kann mit dem Index durchgeführt werden:

 postgres=# explain (costs off) select * from sites where url like 'postgresp%ru'; 

  QUERY PLAN ------------------------------------------------------------------------------ Index Only Scan using sites_url_idx on sites Index Cond: ((url ~>=~ 'postgresp'::text) AND (url ~<~ 'postgresq'::text)) Filter: (url ~~ 'postgresp%ru'::text) (3 rows) 

Tatsächlich wird der Index verwendet, um Werte zu finden, die größer oder gleich "postgresp", aber kleiner als "postgresq" (Index Cond) sind, und dann werden übereinstimmende Werte aus dem Ergebnis ausgewählt (Filter).

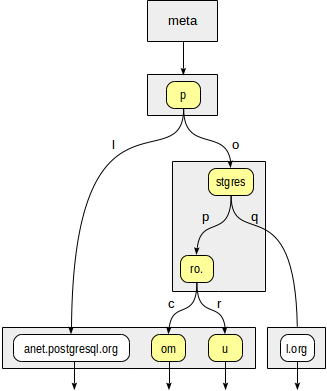
Zunächst muss die Konsistenzfunktion entscheiden, zu welchen untergeordneten Knoten der "p" -Wurzel wir absteigen müssen. Es stehen zwei Optionen zur Verfügung: "p" + "l" (kein Abstieg erforderlich, was auch ohne tieferes Tauchen klar ist) und "p" + "o" + "stgres" (Abstieg fortsetzen).

Für den Knoten "stgres" ist ein erneuter Aufruf der Konsistenzfunktion erforderlich, um "postgres" + "p" + "ro" zu überprüfen. (Abstieg fortsetzen) und "postgres" + "q" (kein Abstieg erforderlich).

Für "ro". Bei einem Knoten und allen untergeordneten Blattknoten antwortet die Konsistenzfunktion mit "Ja", sodass die Indexmethode zwei Werte zurückgibt: "postgrespro.com" und "postgrespro.ru". Ein passender Wert wird in der Filterphase ausgewählt.

Interna

Beim Durchsuchen der Baumstruktur müssen die Datentypen berücksichtigt werden:

 postgres=# select * from spgist_print('sites_url_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix text, -- prefix type node_label smallint, -- label type leaf_value text -- leaf node type ) order by tid, n; 

Eigenschaften

Schauen wir uns die Eigenschaften der SP-GiST-Zugriffsmethode an (Abfragen wurden früher bereitgestellt ):

  amname | name | pg_indexam_has_property --------+---------------+------------------------- spgist | can_order | f spgist | can_unique | f spgist | can_multi_col | f spgist | can_exclude | t 

SP-GiST-Indizes können nicht zum Sortieren und zur Unterstützung der eindeutigen Einschränkung verwendet werden. Darüber hinaus können solche Indizes nicht für mehrere Spalten erstellt werden (im Gegensatz zu GiST). Es ist jedoch zulässig, solche Indizes zur Unterstützung von Ausschlussbeschränkungen zu verwenden.

Die folgenden Indexschicht-Eigenschaften sind verfügbar:

  name | pg_index_has_property ---------------+----------------------- clusterable | f index_scan | t bitmap_scan | t backward_scan | f 

Der Unterschied zu GiST besteht darin, dass Clustering nicht möglich ist.

Und schließlich sind die folgenden Eigenschaften der Spaltenschicht:

  name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f distance_orderable | f returnable | t search_array | f search_nulls | t 

Das Sortieren wird nicht unterstützt, was vorhersehbar ist. Entfernungsoperatoren für die Suche nach nächsten Nachbarn sind in SP-GiST bisher nicht verfügbar. Diese Funktion wird höchstwahrscheinlich in Zukunft unterstützt.

Es wird in PostgreSQL 12, dem Patch von Nikita Glukhov, unterstützt.

SP-GiST kann zumindest für die besprochenen Operatorklassen für den Nur-Index-Scan verwendet werden. Wie wir gesehen haben, werden in einigen Fällen indizierte Werte explizit in Blattknoten gespeichert, während in den anderen Fällen die Werte während des Baumabstiegs Teil für Teil rekonstruiert werden.

Nullen

Um das Bild nicht zu komplizieren, haben wir bisher keine NULL-Werte erwähnt. Aus den Indexeigenschaften geht hervor, dass NULL-Werte unterstützt werden. Wirklich:

 postgres=# explain (costs off) select * from sites where url is null; 

  QUERY PLAN ---------------------------------------------- Index Only Scan using sites_url_idx on sites Index Cond: (url IS NULL) (2 rows) 

NULL ist jedoch für SP-GiST etwas Fremdes. Alle Operatoren aus der Operatorklasse "spgist" müssen streng sein: Ein Operator muss NULL zurückgeben, wenn einer seiner Parameter NULL ist. Die Methode selbst stellt dies sicher: NULL-Werte werden einfach nicht an Operatoren übergeben.

Um die Zugriffsmethode für den Nur-Index-Scan zu verwenden, müssen NULL-Werte ohnehin im Index gespeichert werden. Und sie werden gespeichert, aber in einem separaten Baum mit eigener Wurzel.

Andere Datentypen

Neben Punkten und Radixbäumen für Strings sind auch andere auf SP-GiST basierende Methoden in PostgreSQL implementiert:

• Die Operatorklasse Box_ops bietet einen Quadtree für Rechtecke.
  Jedes Rechteck wird durch einen Punkt in einem vierdimensionalen Raum dargestellt , sodass die Anzahl der Quadranten gleich 16 ist. Ein Index wie dieser kann die Leistung von GiST übertreffen, wenn es viele Schnittpunkte der Rechtecke gibt: In GiST ist es unmöglich, Grenzen zu zeichnen um sich überschneidende Objekte voneinander zu trennen, während es keine derartigen Probleme mit Punkten gibt (auch nicht vierdimensional).
  
• Die Operatorklasse "Range_ops" bietet einen Quadtree für Intervalle.
  Ein Intervall wird durch einen zweidimensionalen Punkt dargestellt : Die untere Grenze wird zur Abszisse und die obere Grenze wird zur Ordinate.
  

Lesen Sie weiter .