🤦🏿 👃🏿 😉 Wir modellieren den MUSIC-Algorithmus zur Bestimmung der Ankunftsrichtung einer elektromagnetischen Welle ✈️ 🧝🏾 😏

Aaspcats

Vorwort

Ich werde meine Einführung von weitem beginnen. Es war einmal, dass Ihr bescheidener Diener im fernen Jahr 2016-2017 einen sechsmonatigen Schulungskurs in der fernen Stadt Ilmenau (Deutschland) absolvierte, wo er das Masterstudium Kommunikation und Signalverarbeitung (im Großen und Ganzen) erfolgreich abschloss. Das Programm war nicht einfach, aber jetzt ist es sogar angenehm, sich daran zu erinnern. Manchmal ...

Am Ende dieser Ausbildung hatte ich neben dem Diplom noch einige verschiedene Materialien zur Hand, die ich für falsch hielt, nicht zu teilen.

Eines dieser Materialien liegt vor Ihnen.

Welche Ziele habe ich bei der Vorbereitung des Seminars verfolgt :

über einige bereits etablierte, „intelligente“ Ansätze zum Thema Antennenarrays sprechen, die am besten zugänglich sind, und dies auf Russisch;
Führen Sie eine kleine Simulation in der Sprache Python 3 durch , um andere Funkingenieure dazu zu bewegen, sich die Programmiersprachen genauer anzusehen (falls Sie dies noch nicht genau untersucht haben).
Stellen Sie Links zu guter englischsprachiger Literatur bereit - ohne fremde Quellen zu lesen, leider nirgendwo.

Was zu beachten ist :

Die MUSIC-Methode (MUltiple SIgnal Classification) - dies bezieht sich tatsächlich auf die Vorschau.

Ein Beispiel für die Diagrammbildung und die MVDR-Methode finden Sie hier (wenn Sie Fragen oder Vorschläge für zusätzliches Material haben, können Sie die Diskussion auf Github.Gist fortsetzen).

Wie ich oben sagte, werden wir Python verwenden, nämlich:

import numpy as np import matplotlib.pyplot as plt

Warum nicht MATLAB, einer der beliebtesten und bequemsten Kandidaten für die lineare Algebra-Modellierung? Weil ich zeigen möchte, dass ähnliche Arbeiten in Python ausgeführt werden können und der Umfang von Python viel größer ist als der von MATLAB. Daher ist es meiner Meinung nach nützlich, mit der Python-Syntax vertraut zu sein.

Fangen wir an!

Formeln werden über https://upmath.me/ erstellt . Vielen Dank an die Macher für ein tolles Tool!

Erklärung des Problems

Angenommen, es gibt eine lineare Antennenanordnung, die aus einer Anzahl von Elementen besteht, die voneinander beabstandet sind $\ Delta = \ frac {\ lambda} {2}$ (Schritt des Antennenarrays), wo $\ lambda$ - die Länge der elektromagnetischen Trägerwelle (EM).

Elektromagnetische Wellen fallen aus verschiedenen Richtungen auf dieses Antennenarray.

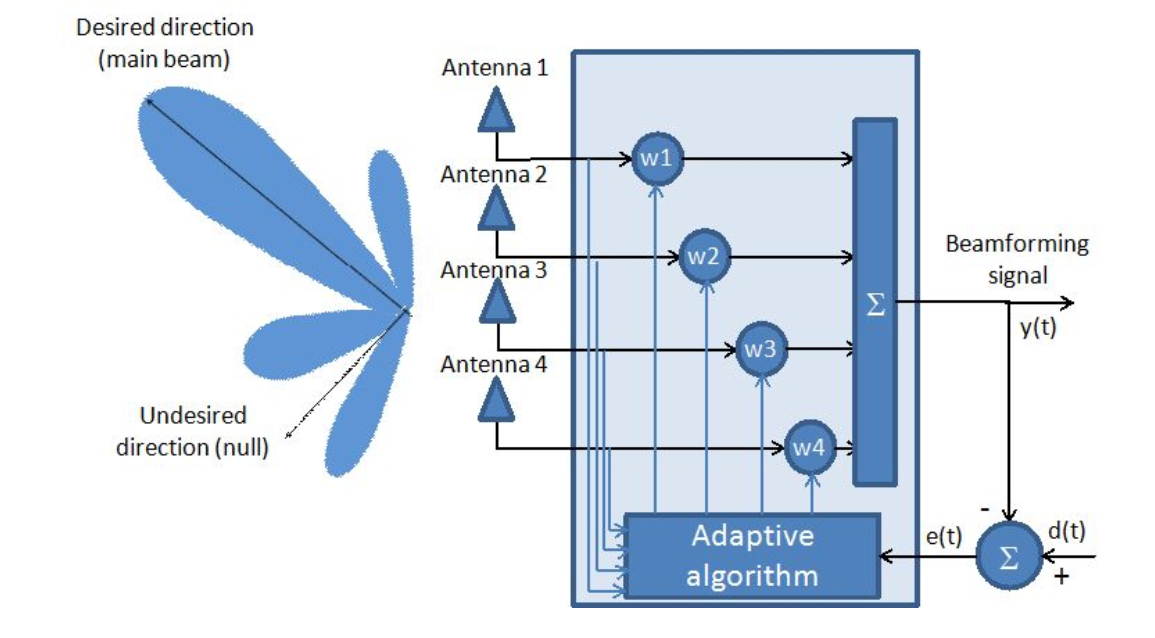
Abb. 1. Adaptives Antennensystem.

Wie aus der Figur ersichtlich ist, wird das Antennenarray als adaptives Filter betrachtet.

Finden des optimalen Koeffizientenvektors ( $\ mathbf {w} _ {opt}$ ) ist die Hauptaufgabe adaptiver Antennenarrays aus mathematischer Sicht.

Zunächst wissen wir nicht, aus welchen bestimmten Richtungen die Signale kommen und wie viele davon. Um diesen Widerspruch aufzulösen, verwenden wir den MUSIC-Algorithmus, einen Algorithmus zur Schätzung von Raumfrequenzen mit hoher Auflösung.

Empfangssignalsimulation

Wir können das Modell des empfangenen Signals durch die Formel darstellen:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

wo $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - Matrix von Abtastvektoren (Lenkvektoren) des Antennenarrays ( $a_i = \ exp (-j \ mu m_i)$ , $m = 0, 1 ... (M-1)$ , $M.$ - die Anzahl der Elemente des Antennenarrays, $d$ - die Anzahl der EM-Wellenquellen, $\ Theta$ - Winkel der Ankunftsrichtung der EM-Welle), $\ mathbf {S}$ - Matrix der übertragenen Zeichen und $\ mathbf {N}$ - Matrix des additiven Rauschens.

Abb. 2. Omnidirektionales lineares Antennenarray (ULAA - Uniform Linear Antennenna Array) [1, S. 32].

Lassen Sie uns diese Formel auf "alltägliche" Weise überdenken: Auf unserem Gitter bekommen wir etwas "Durcheinander" von verschiedenen Signalen, die wir mit bezeichnen $\ mathbf {X}$ . Wir erhalten keine expliziten Informationen über die Anzahl der Quellen und Richtungen, Informationen darüber sind jedoch im empfangenen Signal enthalten.

Wir fangen an zu suchen!

Um dies zu tun, gehen sie normalerweise zu Manipulationen nicht mit den Matrizen komplexer Signalamplituden selbst über, sondern mit ihren Kovarianzen (d. H. Im Wesentlichen mit Potenzen):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

Bedingungen

Wir führen eine wichtige Bedingung ein, die berücksichtigt werden muss: die Rayleigh-Winkelauflösungsgrenze:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

wo $D = M \ Delta$ Ist die Länge des linearen Gitters.

Wir definieren den Ankunftswinkel einer elektromagnetischen Welle durch das Konzept der Ortsfrequenz neu:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

wo $\ mu_R$ - Es gibt eine Standardbreite der Hauptkeule des Strahls ( Standardstrahlbreite ).

Um zu überprüfen, wie effektiv unsere Methode ist und unter welchen Bedingungen, führen wir einige vorgegebene Werte für den Winkelabstand ein:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - Aufteilung in eine Strahlbreite;
$\ mu_1 = -0,5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,5 \ mu_R \ quad$ - Aufteilung in eine zweite Strahlbreite;
$\ mu_1 = -0,3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,3 \ mu_R \ quad$ - Aufteilung in drei Zehntel der Strahlbreite.

Definieren Sie die Eingabeparameter:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

Ein bisschen Theorie über die Methode selbst

Zunächst stellen wir fest, dass der Vorläufer der MUSIC-Methode die Pisarenko- Methode (1973) ist. Das betrachtete Problem der Pisarenko-Methode bestand darin, die Frequenzen der Summe komplexer Exponentiale in weißem Rauschen abzuschätzen. V. F. Pisarenko zeigte, dass Frequenzen von Eigenvektoren gefunden werden können, die dem minimalen Eigenwert der Autokorrelationsmatrix entsprechen. In der Folge wurde diese Methode ein Sonderfall der MUSIC-Methode. [2, S. 459]

Schmidt und seine Kollegen schlugen 1979 den Multiple Signal Classification Algorithm (MUSIC) vor [4]. Der Hauptansatz dieses Algorithmus besteht darin, die Kovarianzmatrix des empfangenen Signals in Eigenwerte zu zerlegen. Da dieser Algorithmus unkorreliertes Rauschen berücksichtigt, hat die erzeugte Kovarianzmatrix eine diagonale Form. Hier werden die Signal- und Rauschunterräume unter Verwendung der linearen Algebra berechnet und sind orthogonal zueinander. Daher verwendet der Algorithmus die Orthogonalitätseigenschaft, um Signal- und Rauschunterräume zu extrahieren [5].

Der verallgemeinerte MUSIC-Algorithmus kann wie folgt definiert werden:

Finden Sie die Kovarianzmatrix $\ mathbf {R} _ {xx}$
Finden Sie Eigenvektoren über EVD oder einen anderen geeigneten numerischen Algorithmus:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

Finden Sie das Pseudospektrum (warum mit dem Präfix Pseudo, wir werden unten diskutieren) MUSIK durch die folgende Formel:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limit_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

wo $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T.$ Liegt der Exponentialvektor für die Frequenz ω in einem gegebenen Bereich und $\ mathbf {u} _i$ - der i-te Eigenvektor (Eigenvektor) der Kovarianzmatrix (1) entsprechend dem Rauschunterraum der Matrix (1) - daher die Indexierung mit $d + 1$ ( $d$ Ist der Rang der Matrix (1)).

Versuchen Sie zur besseren Übersichtlichkeit, das entsprechende MATLAB-Skript auszuführen, das als Referenz bereitgestellt wird. Achten Sie auf zwei Hauptpunkte:
Anstatt das Quadrat der zweiten Norm im Nenner (2) zu berechnen, wenden die Autoren den FFT-Algorithmus auf Eigenvektoren an, was die Modellierung durch Verwendung integrierter Funktionen erleichtert und der Theorie im Allgemeinen aus mathematischer Sicht nicht widerspricht.
Die Kovarianzmatrix wird durch Faltungsmatrizen berechnet. Ein anderer Ansatz wurde oben gezeigt, um räumliche Frequenzen abzuschätzen.

Wie Sie dem Namen entnehmen können, ist MUSIC auch eine klassische Methode zur Schätzung der Empfangsrichtung mit hoher Auflösung. Der Algorithmus zur Berechnung von Pseudospektren in diesem Zusammenhang ist nachstehend angegeben:

wir finden die Kovarianzmatrix des empfangenen Signals;
Finde den Null-Unterraum $\ mathbf {U} _0$ ::

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

Wählen Sie einen Suchbereich aus:

$a (\ mu) = \ begin {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

wo $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

Berechnen Sie das Pseudospektrum:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

Die Beziehung zwischen der Spektralanalyse und der Analyse der Ankunftswinkel (DoA - Arriaval-Richtung) von EM-Wellen ist in Tabelle 1 beschrieben.

Tabelle 1 Kommunikation zwischen MUSIC-Anwendungen : Signalarray-Verarbeitung und Oberschwingungssuche [6].

Variable	Signalarray-Verarbeitung	Harmonische Suche
$M.$	Anzahl der Sensoren	Die Anzahl der Zeiträume
$N.$	Die Anzahl der Zeiträume	Anzahl der Experimente
$d$	Anzahl der Wellenfronten	Die Anzahl der komplexen Komponenten
$\ mu$	Raumfrequenzen	Normalisierte Frequenzen

Im Allgemeinen kann der Prozess des Empfangens durch Arrays (Gitter) mit dem Prozess der klassischen Diskretisierung verglichen werden, weil Tatsächlich führt jeder Sensor, der eine Welle mit einer bestimmten Phasenverzögerung (d. h. mit einer bestimmten Zeitverzögerung) empfängt, die Funktionen eines Abtastdelta-Impulses aus. Die Anzahl der Realisierungen (Experimente) der klassischen Spektralanalyse entspricht der Anzahl der Zeitsegmente (Schnappschüsse). Jede Quelle hat ihre eigene Wellenfront, was bei der Spektralanalyse der Anzahl der eindeutigen Sinuskurven des Signals entspricht.

Und jetzt zurück zum Moment der Berechnung der Eigenvektoren. Wir haben oben bereits diese Vektoren erwähnt $a (\ theta_i) \ epsilon A.$ wo $i = 1,2, .., d$ sind orthogonal zum Rauschunterraum der Kovarianzmatrix, d.h.

$a (\ theta_i) ^ TU_0 = 0 ^ T.$

Tatsächlich sehen wir ein Gleichungssystem, in dem wir die Wurzeln finden können - Eigenvektoren. Ein solches Verfahren ermöglicht es im Gegensatz zu numerischen Algorithmen (für die, wie oben erwähnt, für EVD gilt), eher reale als ungefähre Eigenwerte zu erhalten. Deshalb können wir mit diesem Ansatz kein Pseudospektrum, sondern ein Spektrum erhalten. Die gleiche Idee bildete die Grundlage des Root-MUSIC- Algorithmus.

Modellierung

Fuf! Schließlich werden alle Formeln beschrieben und etwas erklärt. Wir können mit dem Modellieren beginnen.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

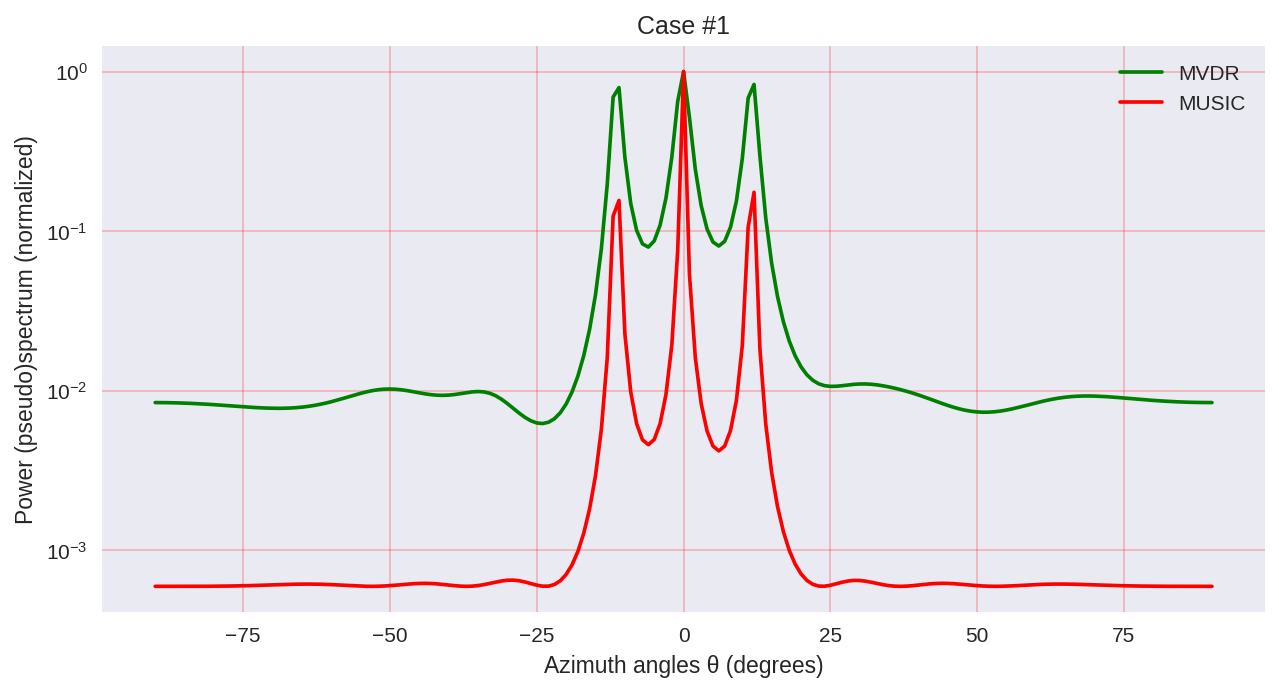
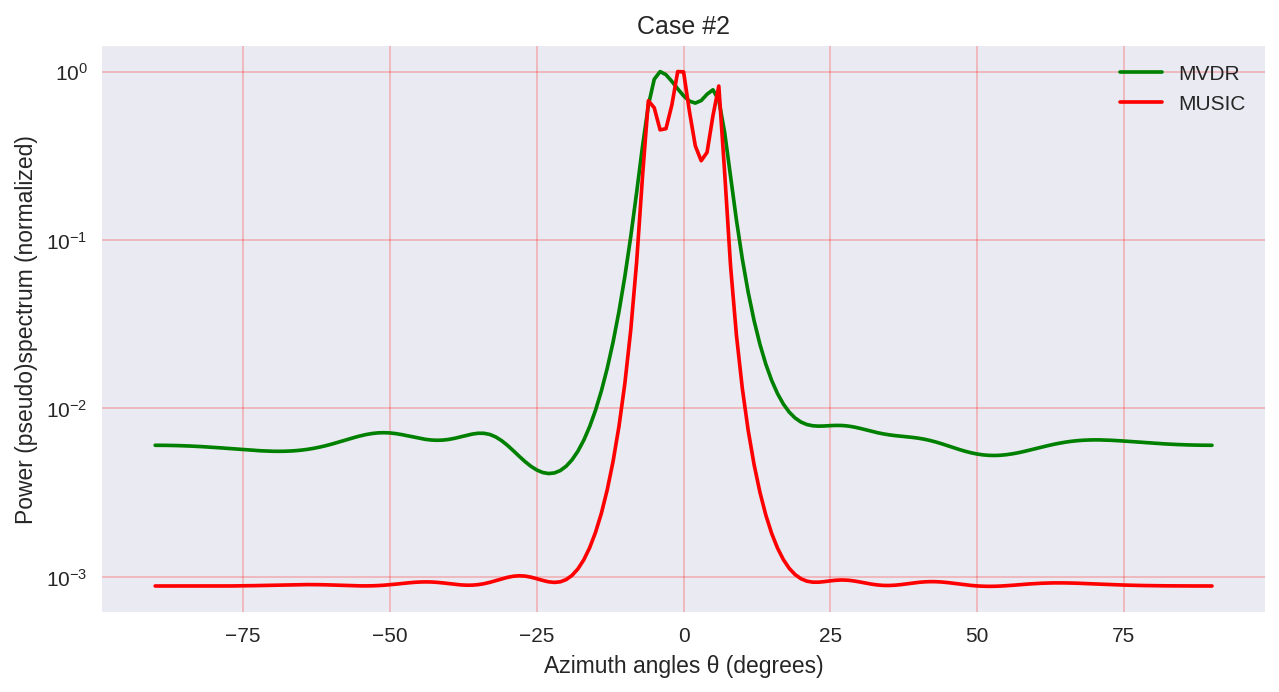
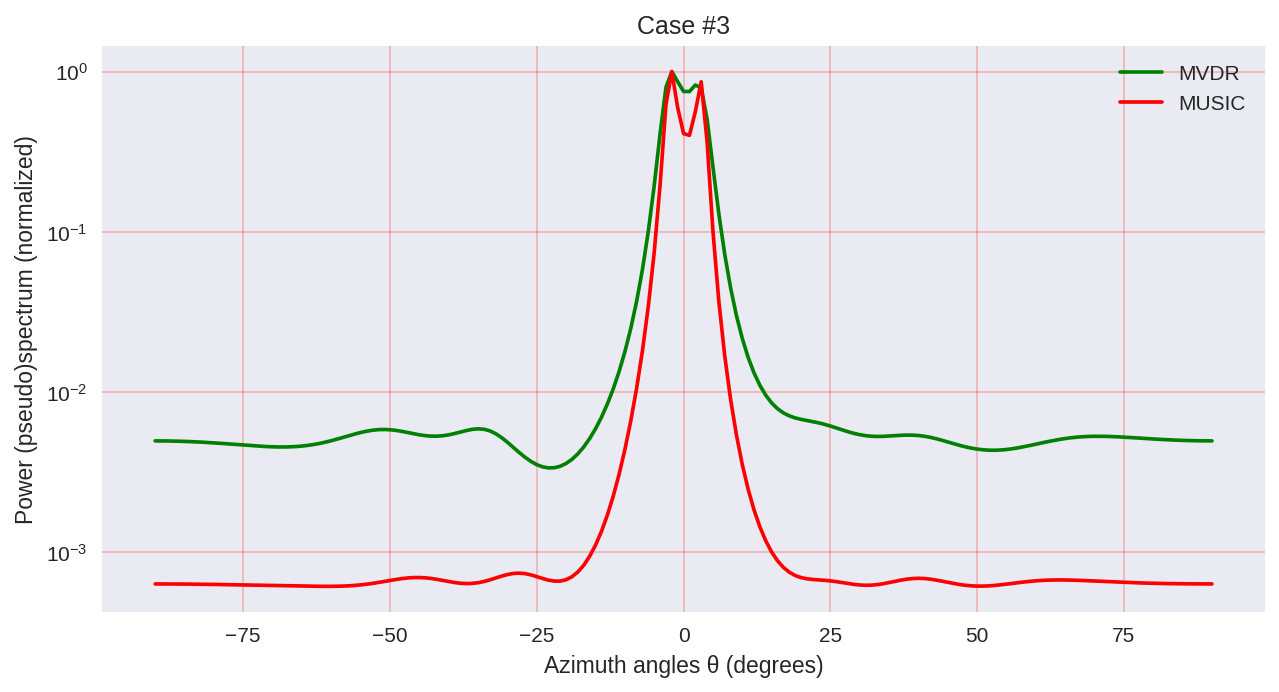
Wie wir sehen können, hat MUSIC eine höhere Auflösung und ermöglicht im Allgemeinen bessere Ergebnisse als beispielsweise MVDR - der gleiche Vertreter parametrischer Methoden der Spektralanalyse.

Es sollte jedoch berücksichtigt werden, dass wir bei der Verwendung von MUSIC rechenintensivere Algorithmen wie EVD oder SVD verwenden, was für eine höhere Genauigkeit mit einem gewissen Preis verbunden ist.

Solche Dinge.

Liste der verwendeten Literatur:

Haykin, Simon und KJ Ray Liu. Handbuch zur Array-Verarbeitung und zu Sensornetzwerken. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Hayes MH Statistische digitale Signalverarbeitung und Modellierung. - John Wiley & Sons, 2009.
Haykin, Simon S. Adaptive Filtertheorie. Pearson Education India, 2008. pp. 422-427
Richmond, Christ D. "Capon-Algorithmus mittlere quadratische Fehlerschwelle SNR-Vorhersage und Wahrscheinlichkeit der Auflösung." IEEE Transactions on Signal Processing 53.8 (2005): 2748 & ndash; 2764.
SKP Gupta, MUSIC und verbesserter MUSIC-Algorithmus zur Vermeidung der Ankunftsdorektion, IEEE, 2015.
Vorlesungen von Professor Martin Haardt ( Array Array )

Wir modellieren den MUSIC-Algorithmus zur Bestimmung der Ankunftsrichtung einer elektromagnetischen Welle