Deep Learning in der optischen Flussberechnung

Mit dem Aufkommen vieler verschiedener neuronaler Netzwerkarchitekturen gehören viele klassische Computer Vision-Techniken der Vergangenheit an. Immer seltener verwenden Menschen SIFT und HOG zur Objekterkennung und MBH zur Aktionserkennung. Wenn sie es verwenden, ähneln sie eher handgefertigten Zeichen für die entsprechenden Gitter. Heute werden wir uns eines der klassischen CV-Probleme ansehen, bei denen die klassischen Methoden immer noch die Führung übernehmen, während DL-Architekturen sie träge in den Hinterkopf atmen.

Optische Durchflussschätzung

Die Aufgabe der Berechnung des optischen Flusses zwischen zwei Bildern (normalerweise zwischen benachbarten Bildern eines Videos) besteht darin, ein Vektorfeld zu konstruieren $$$O$die gleiche Größe im Übrigen $$$O (i, j)$entspricht dem scheinbaren Pixelverschiebungsvektor $$$(i, j)$vom ersten bis zum zweiten Frame. Indem wir ein solches Vektorfeld zwischen allen benachbarten Bildern des Videos erstellen, erhalten wir ein vollständiges Bild davon, wie sich bestimmte Objekte darauf bewegt haben. Mit anderen Worten, dies ist die Aufgabe, alle Pixel in einem Video zu verfolgen. Der optische Strom wird sehr häufig verwendet - bei Aufgaben zur Aktionserkennung können Sie sich beispielsweise mit einem solchen Vektorfeld auf die Bewegungen konzentrieren, die auf dem Video auftreten, und sich von seinem Kontext entfernen [7]. Noch häufigere Anwendungen sind visuelle Kilometerzähler, Videokomprimierung, Nachbearbeitung (z. B. Hinzufügen eines Zeitlupeneffekts) und vieles mehr.



Es gibt Raum für einige Unklarheiten - was genau wird aus mathematischer Sicht als sichtbare Verzerrung angesehen? Normalerweise wird angenommen, dass die Pixelwerte ohne Änderungen von einem Bild zum nächsten gehen, mit anderen Worten:

$$

$$I (i, j, t) = I (i + u_i, j + u_j, t + 1),$$

wo $$$I (i, j, t)$- Pixelintensität in Koordinaten $$$(i, j)$dann optischer Fluss $$$(u_i, u_j)$zeigt, wo sich dieses Pixel zum nächsten Zeitpunkt bewegt hat (d. h. im nächsten Bild).

Auf dem Bild sieht es so aus:





Das Visualisieren eines Vektorfeldes direkt mit Vektoren ist visuell, aber nicht immer bequem. Daher besteht die zweite übliche Methode darin, mit Farbe zu visualisieren:





Jede Farbe in diesem Bild codiert einen bestimmten Vektor. Der Einfachheit halber werden Vektoren, die länger als 20 sind, zugeschnitten, und der Vektor selbst kann anhand der Farbe aus dem folgenden Bild wiederhergestellt werden:




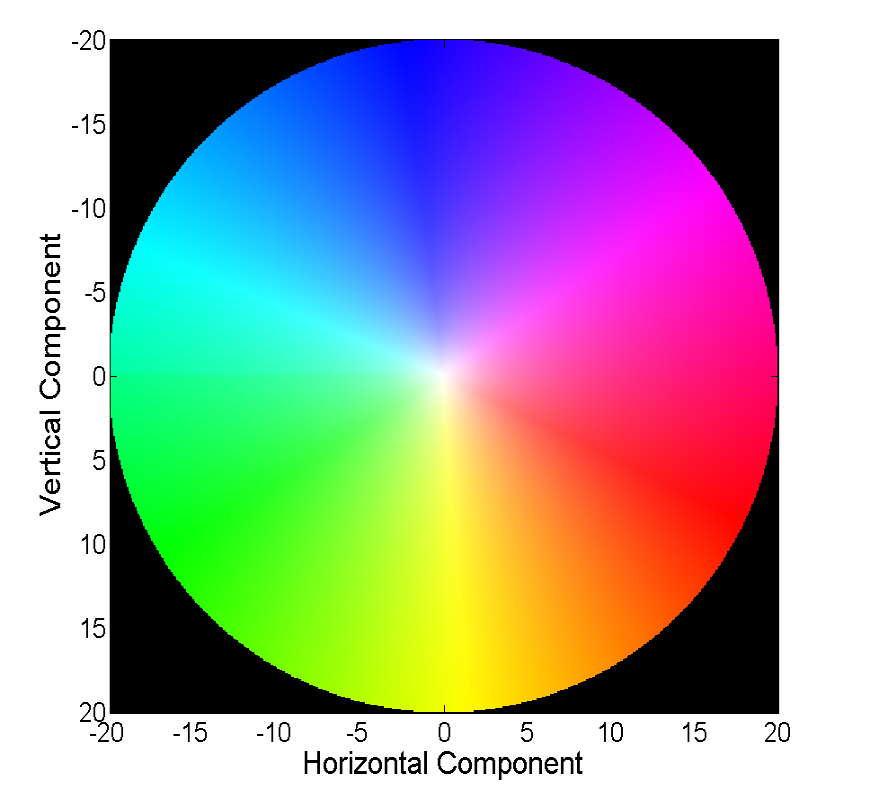
Klassische Methoden haben eine ziemlich gute Genauigkeit erreicht, die manchmal ihren Preis hat. Wir werden die Fortschritte betrachten, die neuronale Netze bei der Lösung dieses Problems in den letzten 4 Jahren erzielt haben.

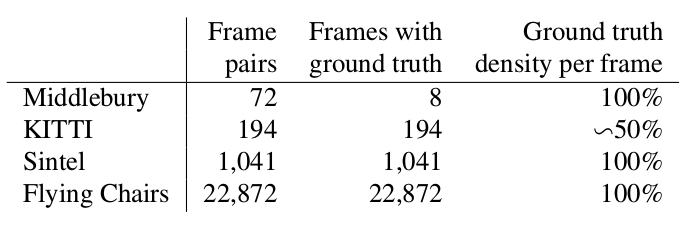
Daten und Metriken

Zwei Wörter darüber, welche Datensätze zu Beginn unserer Geschichte (d. H. 2015) verfügbar und beliebt waren und wie sie die Qualität des resultierenden Algorithmus messen.

Middlebury

Ein winziger Datensatz von 8 Bildpaaren mit kleinen Offsets, der jedoch auch jetzt noch zur Validierung von Algorithmen zur Berechnung des optischen Flusses verwendet wird.

Kitty

Dies ist ein Datensatz, der für Anwendungen für selbstfahrende Autos gekennzeichnet und mit LIDAR-Technologie zusammengestellt wurde. Es wird häufig zur Validierung von Algorithmen zur Berechnung des optischen Flusses verwendet und enthält viele ziemlich komplizierte Fälle mit scharfen Übergängen zwischen Frames.

Sintel

Ein weiterer sehr verbreiteter Maßstab, der auf der Grundlage des offenen und in Blender gezeichneten Cartoon Sintel in zwei Versionen erstellt wurde, die als sauber und endgültig bezeichnet werden. Der zweite ist viel komplizierter, weil enthält viele atmosphärische Effekte, Rauschen, Unschärfe und andere Probleme für die Algorithmen zur Berechnung des optischen Flusses.

EPE

Die Standardfehlerfunktion für die Aufgabe zur Berechnung des optischen Flusses ist Endpunktfehler oder EPE. Dies ist einfach der euklidische Abstand zwischen dem berechneten Algorithmus und dem wahren optischen Fluss, gemittelt über alle Pixel.

Flownet (2015)

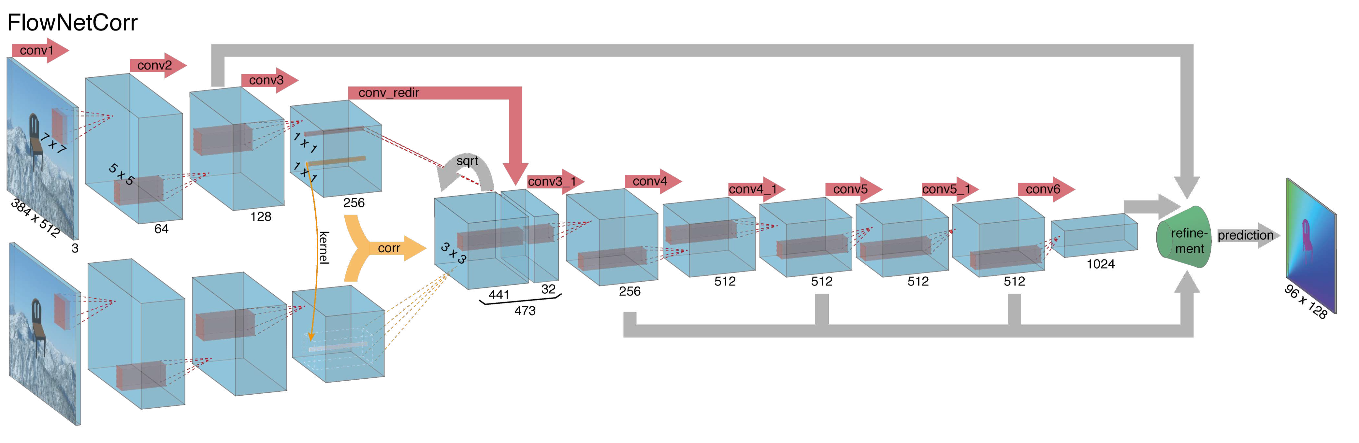
Als die Autoren (von den Universitäten München und Freiburg) 2015 mit dem Aufbau einer neuronalen Netzwerkarchitektur für die Berechnung des optischen Flusses begannen, hatten sie zwei Probleme: Es gab keinen großen markierten Datensatz für diese Aufgabe, und das manuelle Markieren wäre schwierig (versuchen Sie zu markieren, wo ich mich bewegt habe) Erstens jedes Pixel des Bildes im nächsten Bild. Diese Aufgabe war ganz anders als alle Aufgaben, die zuvor mit Hilfe von CNN-Architekturen gelöst wurden. Tatsächlich ist dies eine Aufgabe der Pixel-für-Pixel-Regression, wodurch sie der Aufgabe der Segmentierung (Pixel-für-Pixel-Klassifizierung) ähnelt, aber anstelle eines Bildes haben wir zwei Eingaben, und intuitiv sollten die Zeichen irgendwie den Unterschied zwischen den beiden Bildern zeigen. Als erste Iteration wurde beschlossen, nur zwei RGB-Frames als Eingabe zu platzieren (nachdem tatsächlich ein 6-Kanal-Bild empfangen wurde), zwischen denen wir den optischen Strom berechnen möchten, und U-net als Architektur mit einer Reihe von Änderungen zu verwenden. Dieses Netzwerk wurde FlowNetS genannt (S steht für Simple):





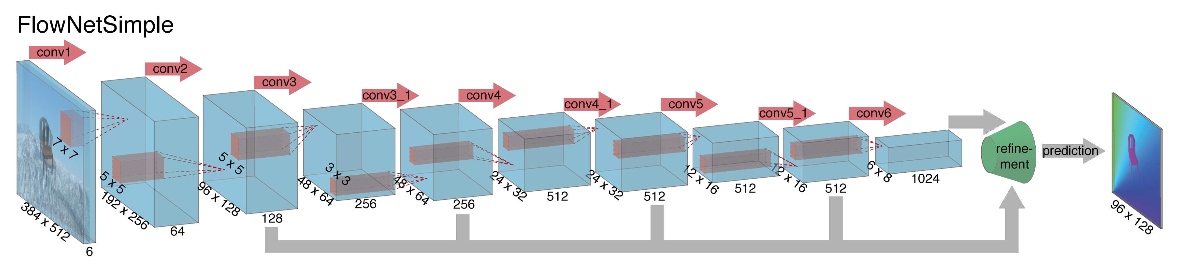
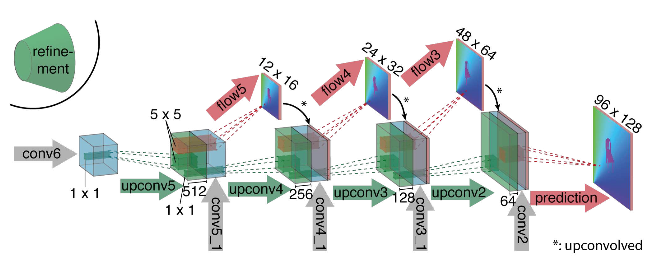
Wie Sie dem Diagramm entnehmen können, fällt der Encoder nicht auf, der Decoder unterscheidet sich in mehreren Punkten von den klassischen Optionen:

1. Die Vorhersage des optischen Flusses erfolgt nicht nur von der letzten Ebene, sondern auch von allen anderen. Um die Grundwahrheit für die i-te Ebene des Decoders zu erhalten, wird das ursprüngliche Ziel (d. H. Der optische Strom) einfach (fast das gleiche wie das Bild) auf die gewünschte Auflösung reduziert, und das auf der i-ten Ebene erhaltene Prädikat geht weiter, t es wird mit einer Merkmalskarte verkettet, die aus dieser Ebene hervorgeht. Die allgemeine Funktion des Lernverlusts ist eine gewichtete Summe der Verluste von allen Ebenen des Decoders, während die Gewichtung selbst umso größer ist, je näher die Ebene an der Netzwerkausgabe liegt. Die Autoren geben keine Erklärung dafür, warum dies getan wird, aber höchstwahrscheinlich liegt der Grund darin, dass scharfe Bewegungen auf frühen Ebenen besser zu erkennen sind, dann sind die Vektoren im optischen Strom mit niedrigerer Auflösung nicht so groß.
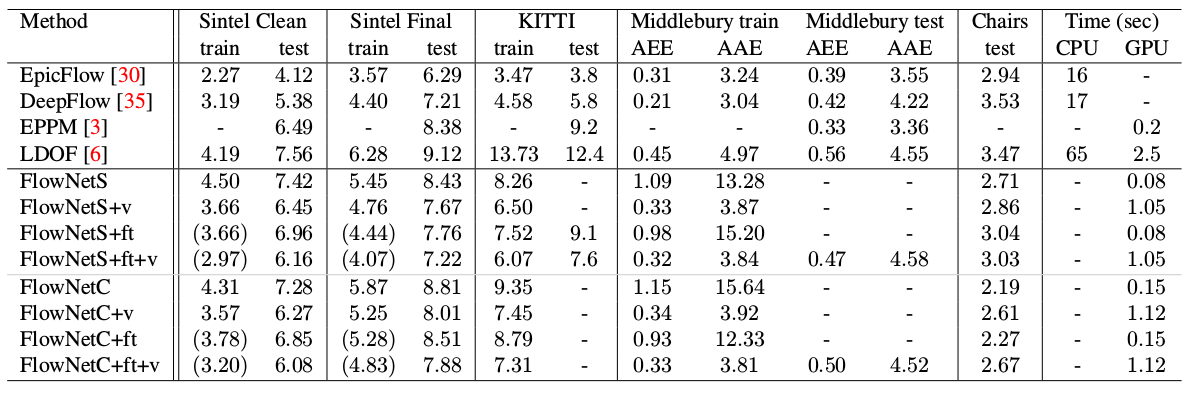
2. Das Diagramm zeigt, dass die Eingangsauflösung der Bilder 384 x 512 beträgt und die Ausgabe viermal kleiner ist. Die Autoren stellten fest, dass, wenn Sie diese Ausgabe durch einfache bilineare Interpolation auf 384 x 512 erhöhen, die gleiche Qualität erzielt wird, als würden Sie zwei weitere Ebenen des Decoders anschließen. Sie können auch den Variationsansatz [2] verwenden, der die Qualität beweist (+ v in der Tabelle mit Qualität).
3. Wie in U-net werden Attributkarten vom Codierer an den Decodierer gesendet und wie in der Abbildung gezeigt verkettet.

Um zu verstehen, wie die Autoren versucht haben, ihre Basislinie zu verbessern, müssen Sie wissen, wie die Korrelation zwischen Bildern ist und warum sie bei der Berechnung des optischen Flusses hilfreich sein kann. Wenn wir also zwei Bilder haben und wissen, dass das zweite das nächste Bild im Video relativ zum ersten ist, können wir versuchen, den Bereich um den Punkt im ersten Bild (für den wir eine Verschiebung zum zweiten Bild finden möchten) mit Bereichen gleicher Größe im zweiten Bild zu vergleichen. Unter der Annahme, dass die Verschiebung pro Zeiteinheit nicht zu groß sein könnte, kann der Vergleich nur in einer bestimmten Nachbarschaft des Startpunkts betrachtet werden. Hierzu wird eine Kreuzkorrelation verwendet. Lassen Sie uns anhand eines Beispiels veranschaulichen.

Nehmen Sie zwei benachbarte Bilder des Videos. Wir möchten feststellen, wo sich ein bestimmter Punkt vom ersten zum zweiten Bild verschoben hat. Angenommen, ein Bereich um diesen Punkt hat sich auf die gleiche Weise verschoben. In der Tat werden benachbarte Pixel in einem Video normalerweise zusammen versetzt, wie z höchstwahrscheinlich sind sie visuell Teil eines Objekts. Diese Annahme wird beispielsweise in differenziellen Ansätzen aktiv verwendet, die in [5], [6] ausführlicher gelesen werden können.

fig, ax = plt.subplots(1, 2, figsize=(20, 10)) ax[0].imshow(frame1) ax[1].imshow(frame2); 

Versuchen wir, einen Punkt in der Mitte der Pfote des Kätzchens zu finden und ihn im zweiten Bild zu finden. Nehmen Sie einen Bereich um ihn herum.

 patch1 = frame1[90:190, 140:250] plt.imshow(patch1); 

Wir berechnen die Korrelation zwischen diesem Bereich (in der englischen Literatur wird häufig eine Vorlage oder ein Patch aus dem ersten Bild geschrieben) und dem zweiten Bild. Die Vorlage „geht“ einfach durch das zweite Bild und berechnet den folgenden Wert zwischen sich und Teilen gleicher Größe im zweiten Bild:



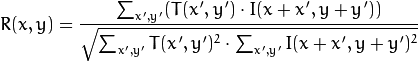
Je größer der Wert dieses Werts ist, desto mehr sieht die Vorlage wie das entsprechende Stück im zweiten Bild aus. Mit OpenCV kann dies folgendermaßen geschehen:

 corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED) plt.imshow(corr, cmap='gray'); 

Weitere Details finden Sie in [7].

Das Ergebnis ist wie folgt:



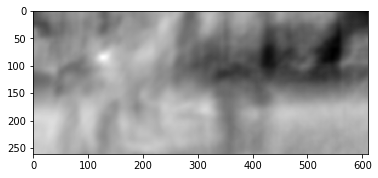
Wir sehen einen klaren Peak, der weiß angezeigt wird. Finden Sie es im zweiten Frame:

 min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr) h, w, _ = patch1.shape top_left = max_loc bottom_right = (top_left[0] + w, top_left[1] + h) frame2_copy = frame2.copy() cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2) plt.imshow(frame2_copy); 

Wir sehen, dass der Fuß korrekt gefunden wurde. Anhand dieser Daten können wir verstehen, in welche Richtung er sich vom ersten zum zweiten Bild bewegt hat, und den entsprechenden optischen Fluss berechnen. Zusätzlich stellt sich heraus, dass dieser Vorgang gegenüber photometrischen Verzerrungen, d. H. Wenn die Helligkeit im zweiten Bild stark ansteigt, bleibt der Kreuzkorrelationspeak zwischen den Bildern bestehen.

In Anbetracht all dessen entschieden sich die Autoren, die sogenannte Korrelationsschicht in ihre Architektur einzuführen, aber es wurde beschlossen, die Korrelation nicht gemäß den Eingabebildern, sondern gemäß den Attributkarten nach mehreren Schichten des Codierers zu berücksichtigen. Eine solche Schicht hat aus offensichtlichen Gründen keine Lernparameter, obwohl sie im Wesentlichen der Faltung ähnlich ist, aber anstelle von Filtern verwenden wir hier keine Gewichte, sondern einen Bereich des zweiten Bildes:



Seltsamerweise führte dieser Trick zu keiner signifikanten Verbesserung der Qualität der Autoren dieses Artikels. Er wurde jedoch erfolgreicher in weiteren Arbeiten angewendet, und in [9] konnten die Autoren zeigen, dass FlowNetC durch geringfügige Änderung der Trainingsparameter wesentlich besser funktionieren kann.

Die Autoren lösten das Problem mit dem Fehlen eines Datensatzes auf ziemlich elegante Weise: Sie kratzten 964 Bilder von Flickr zu den Themen "Stadt", "Landschaft", "Berg" in der Auflösung 1024 × 768 und verwendeten ihre Ernte 512 × 384 als Hintergrund, die dann einige warf Stühle aus einem offenen Satz gerenderter 3D-Modelle. Dann wurden verschiedene affine Transformationen unabhängig voneinander auf die Stühle und den Hintergrund angewendet, die verwendet wurden, um das zweite Bild in einem Paar und den optischen Fluss zwischen ihnen zu erzeugen. Das Ergebnis ist wie folgt:





Ein interessantes Ergebnis war, dass die Verwendung eines solchen synthetischen Datensatzes es ermöglichte, eine relativ gute Qualität für Daten aus einer anderen Domäne zu erzielen. Die Feinabstimmung der entsprechenden Daten hat natürlich mehr Qualitäten bewiesen (+ ft in der folgenden Tabelle):



Das Ergebnis auf echten Videos ist hier zu sehen:

SpyNet (2016)

In vielen nachfolgenden Artikeln versuchten die Autoren, die Qualität zu verbessern, indem sie das Problem der schlechten Erkennung plötzlicher Bewegungen lösten. Intuitiv wird die Bewegung vom Netzwerk nicht erfasst, wenn ihr Vektor das Empfangsfeld der Aktivierung deutlich überschreitet. Es wird vorgeschlagen, dieses Problem aufgrund von drei Dingen zu lösen: einer größeren Faltung, Pyramiden und dem "Verziehen" eines Bildes von einem Paar in einen optischen Strom. Alles in Ordnung.

Wenn wir also ein paar Bilder haben, in denen sich das Objekt stark verschoben hat (10+ Pixel), können wir das Bild einfach reduzieren (um das 6-fache oder mehr). Der absolute Wert des Versatzes nimmt erheblich ab, und das Netzwerk kann ihn mit größerer Wahrscheinlichkeit „fangen“, insbesondere wenn seine Windungen größer sind als der Versatz selbst (in diesem Fall werden 7x7-Windungen verwendet).



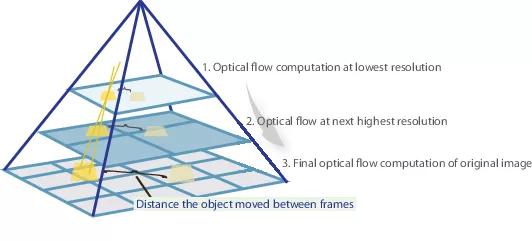
Beim Verkleinern des Bildes haben wir jedoch viele wichtige Details verloren. Daher sollten wir zur nächsten Ebene der Pyramide gehen, in der die Bildgröße bereits größer ist, und dabei die Informationen berücksichtigen, die wir zuvor erhalten haben, als wir den optischen Fluss bei einer kleineren Größe berechnet haben. Dies erfolgt unter Verwendung des Warping-Operators, der das erste Bild gemäß der verfügbaren Annäherung des optischen Flusses (erhalten auf der vorherigen Ebene) wiedergibt. Eine Verbesserung in diesem Fall besteht darin, dass das erste Bild, das gemäß der Annäherung des optischen Flusses "geschoben" wird, näher am zweiten liegt als das ursprüngliche, dh wir reduzieren erneut den absoluten Wert des optischen Flusses, den wir vorhersagen müssen (Rückruf, kleiner Wert) Bewegungen werden viel besser erkannt, da sie vollständig in einer Faltung enthalten sind. Aus mathematischer Sicht kann der Warping-Operator mit einem Bitmap-Bild I und einer Approximation des optischen Flusses V wie folgt beschrieben werden:

$$

$$w (I, V) = I_w, \; \; I_w (x) = I (x + V (x)),$$

wo $$$x = (i, j)$d.h. ein bestimmter Punkt im Bild $$$I$- das Bild selbst $$$V$- optischer Fluss $$$I_w$- das resultierende Bild, "eingewickelt" in den optischen Strom.

Wie kann man all dies in der CNN-Architektur anwenden? Wir legen die Anzahl der Pyramidenebenen fest $$$k$und einen Faktor, um den jedes nachfolgende Bild auf einem Niveau reduziert wird, das vom letzten beginnt $$$n$. Bezeichnen mit $$$d (*)$und $$$u (*)$die Downsampling- und Upsampling-Funktionen des Bildes oder des optischen Flusses um diesen Faktor.

Wir erhalten auch eine Reihe von CNN-ok { $$$G_0 ... G_k$}, eine für jede Ebene der Pyramide. Dann $$$G_i$-th Netzwerk akzeptiert ein paar Bilder mit $$$i$Pyramidenniveau und optischer Fluss berechnet am $$$G_ {i-1}$Niveau ( $$$G_0$akzeptiert stattdessen nur einen Tensor von Nullen). In diesem Fall senden wir eines der Bilder an die Verzerrungsschicht, um den Unterschied zwischen ihnen zu verringern, und wir sagen nicht den optischen Fluss auf dieser Ebene voraus, sondern den Wert, der zu dem erhöhten (hochgetasteten) optischen Fluss von der vorherigen Ebene addiert werden muss, um den optischen Fluss zu erhalten auf dieser Ebene. In der Formel sieht es ungefähr so ​​aus:

$$

$$v_k = G_k (I_k ^ 1, w (I_k ^ 2, u (V_ {k-1})), V_ {k-1})$$

Um den optischen Stream selbst zu erhalten, fügen wir einfach das Netzwerkprädikat und den erhöhten Stream der vorherigen Ebene hinzu:

$$

$$V_k = u (V_ {k-1}) + v_k.$$

Um die Grundwahrheit für das Netzwerk auf dieser Ebene zu erhalten, müssen wir die entgegengesetzte Operation ausführen: Subtrahieren Sie das Prädikat vom Ziel (auf die gewünschte Ebene reduziert) von der vorherigen Ebene der Pyramide. Schematisch sieht es so aus:



Der Vorteil dieses Ansatzes ist, dass wir jede Stufe unabhängig unterrichten können. Die Autoren begannen mit dem Training ab Stufe 0, jedes nachfolgende Netzwerk wurde mit den Parametern des vorherigen initialisiert. Da jedes Netzwerk $$$G_i$löst das Problem viel einfacher als die vollständige Berechnung des optischen Flusses in einem großen Bild, dann können die Parameter viel weniger gemacht werden. So sehr, dass jetzt das gesamte Ensemble auf mobile Geräte passen kann:



Das Ensemble selbst ist wie folgt (ein Beispiel für eine Pyramide mit 3 Ebenen):



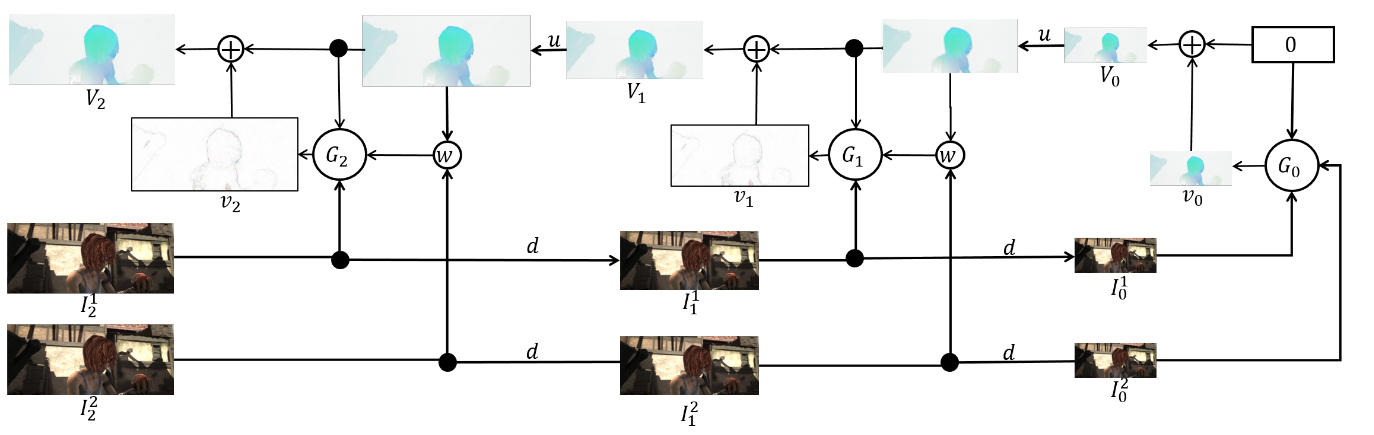
Es bleibt direkt über Architektur zu sprechen $$$G_i$vernetzen und Bilanz ziehen. Jedes Netzwerk $$$G_i$besteht aus 5 Faltungsschichten, von denen jede mit der ReLU-Aktivierung endet, mit Ausnahme der letzten (die den optischen Fluss vorhersagt). Die Anzahl der Filter auf jeder Ebene beträgt jeweils { $$$32, 64, 32, 16, 2$}. Die Eingänge des neuronalen Netzwerks (das Bild, das zweite Bild, das in den optischen Strom „eingewickelt“ ist, und der optische Strom selbst) verketten sich einfach entsprechend der Dimension der Kanäle, sodass ihr Eingangstensor 8 hat. Die Ergebnisse sind beeindruckend:

PWC-Net (2018)

Inspiriert vom Erfolg ihrer deutschen Kollegen beschlossen die Mitarbeiter von NVIDIA, ihre Erfahrungen (und Grafikkarten) einzusetzen, um das Ergebnis weiter zu verbessern. Ihre Arbeit basierte größtenteils auf Ideen des Vorgängermodells (SpyNet), daher wird sich PWC-Net auch mit Pyramiden befassen, jedoch mit Faltungspyramiden, jedoch nicht mit den Originalbildern - in der richtigen Reihenfolge.

Die Verwendung von Rohpixelintensitäten zur Berechnung des optischen Flusses ist nicht immer sinnvoll, da Eine starke Änderung der Helligkeit / des Kontrasts wird unsere Annahme brechen, dass sich Pixel ohne Änderungen von einem Bild zum nächsten bewegen und der Algorithmus solchen Änderungen nicht widersteht. In klassischen Algorithmen zur Berechnung des optischen Flusses werden verschiedene Transformationen verwendet, die diese Situation abschwächen. In diesem Fall haben die Autoren beschlossen, dem Modell die Möglichkeit zu geben, solche Transformationen selbst zu lernen. Daher werden anstelle der Bildpyramide in PWC-Net Faltungspyramiden verwendet (daher der erste Buchstabe in Pwc-Net), d. H. Nur Feature-Maps aus verschiedenen CNN-Layern, die hier als Feature-Pyramiden-Extraktor bezeichnet werden.

Dann ist fast alles wie in SpyNet, kurz bevor Sie bei CNN, dem so genannten optischen Flussschätzer, alles einreichen, was Sie brauchen, nämlich:

• Bild (in diesem Fall eine Feature-Map vom Feature-Pyramiden-Extraktor),
• der auf der vorherigen Ebene berechnete hochgetastete optische Fluss,
• das zweite Bild, „eingewickelt“ (erinnern Sie sich an die Verzerrungsschicht, daher der zweite Buchstabe in pWc-Net), in diesen optischen Strom,

Überlegen Sie zwischen dem „verpackten“ zweiten Frame und dem üblichen ersten (ich erinnere Sie noch einmal daran, dass hier anstelle von Rohbildern Feature-Karten mit Feature-Pyramiden-Extraktor verwendet werden), was als Kostenvolumen bezeichnet wird (daher der dritte Buchstabe in pwC-Net) und was im Wesentlichen bereits vorhanden ist zuvor betrachtete Korrelation zwischen zwei Bildern.



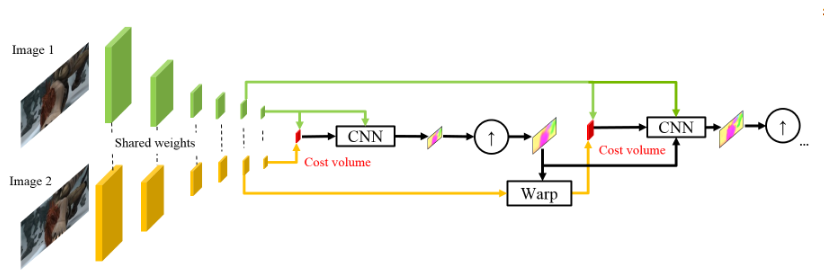
Der letzte Schliff ist das Kontextnetzwerk, das unmittelbar nach dem optischen Flussschätzer hinzugefügt wird und die Rolle der trainierten Nachbearbeitung für den berechneten optischen Strom spielt. Architektonische Details können unter dem Spoiler oder im Originalartikel eingesehen werden.


Die Ergebnisse sind noch beeindruckender:



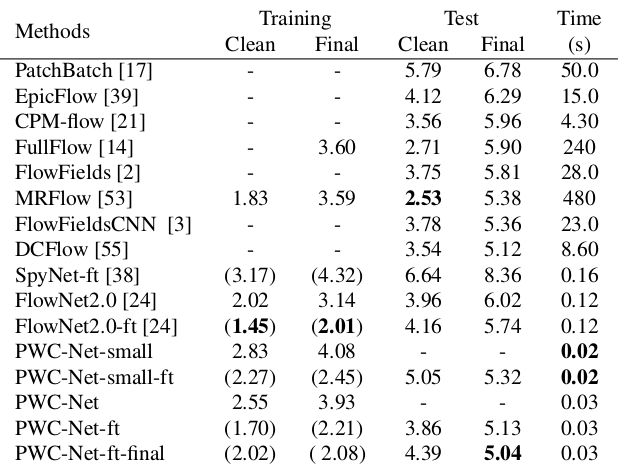
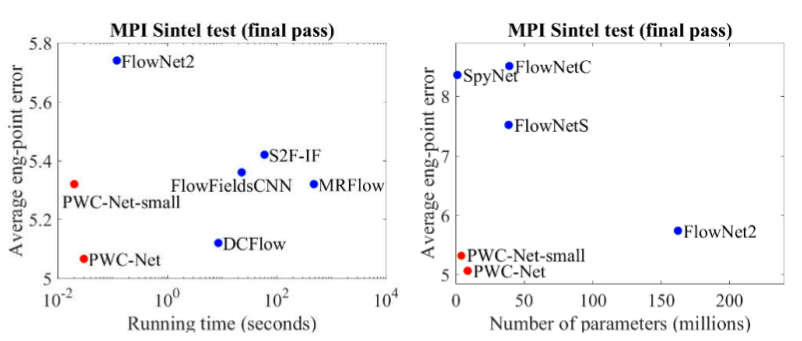
Im Vergleich zu anderen CNN-Methoden zur Berechnung des optischen Flusses erzielt PWC-Net ein Gleichgewicht zwischen Qualität und Anzahl der Parameter:



Es gibt auch eine hervorragende Präsentation der Autoren selbst, in der sie über das Modell selbst und ihre Experimente sprechen:

Fazit

Die Entwicklung von Architekturen, die das Problem der optischen Flusszählung lösen, ist ein wunderbares Beispiel dafür, wie der Fortschritt in CNN-Architekturen und deren Kombination mit klassischen Methoden das beste und beste Ergebnis liefert. Und während klassische CV-Methoden immer noch an Qualität gewinnen, geben die jüngsten Ergebnisse Hoffnung, dass dies behoben werden kann ...

Quellen und Links

1. FlowNet: Lernen des optischen Flusses mit Faltungsnetzwerken: Artikel , Code .
2. Optischer Fluss mit großer Verschiebung: Deskriptoranpassung bei der Schätzung der Variationsbewegung: Artikel .
3. Optische Flussschätzung unter Verwendung eines räumlichen Pyramidennetzwerks: Artikel , Code .
4. PWC-Net: CNNs für den optischen Fluss unter Verwendung von Pyramide, Verzerrung und Kostenvolumen: Artikel , Code .
5. Was Sie über den optischen Fluss wissen wollten, aber es war Ihnen peinlich zu fragen: Artikel .
6. Berechnung des optischen Flusses nach der Lucas-Canada-Methode. Theorie: Artikel .
7. Template Matching mit OpenCVP: Dock .
8. Quo Vadis, Aktionserkennung? Ein neues Modell und der Kinetik-Datensatz: Artikel .
9. FlowNet 2.0: Entwicklung der optischen Flussschätzung mit tiefen Netzwerken: Artikel , Code .