Guten Tag an alle!
In Bezug auf das Thema räumliche Vielfalt haben wir bereits die Probleme des Verblassens in Kommunikationskanälen angesprochen und warum ein solches Verblassen auftritt. Heute schlage ich vor, etwas ausführlicher über dieses Thema zu sprechen.
Darüber hinaus werden wir im heutigen Artikel leicht auf die Fragen der räumlichen Korrelation von MIMO-Kanälen eingehen, die traditionell im Verlauf des Kurses für Mobilkommunikation ( CSP ) von Professor Haardt erörtert werden. Daher wird eine solche Veröffentlichung meiner Meinung nach nicht überflüssig sein. Ich stelle sofort fest, dass die Bandbreite der Probleme nicht nur auf die mobile Kommunikation beschränkt ist.
Im Allgemeinen lade ich alle Interessierten zum Thema drahtlose Kommunikation zum Lesen ein und los geht's!
Colin Slater "Verblassende Erinnerungen" . Ja, alles auf ein Thema zu reduzieren ist wahrscheinlich übertrieben, aber mit einer solchen Metapher können Sie sich vorstellen, was der Empfänger nach allen möglichen Einflüssen auf das ursprüngliche Informationssignal empfängt ...
Worüber reden wir?
Beginnen wir mit der Tatsache, dass es in der Natur sogenannte multiplikative Rauschen gibt , die die empfangene Signalleistung beeinflussen - Fading .
Die Begriffe werden, wie Sie vielleicht vermutet haben, nicht direkt ins Russische und Englische übersetzt, aber dies ist nicht sehr wichtig.In der englischen Literatur impliziert der Begriff Fading einen gewissen Einfluss, der sozusagen dazu führt, dass unser Signal verblasst, "verblasst".
In unserer Literatur wird üblicherweise der Begriff Fading verwendet, und dies ist hauptsächlich auf den Mehrwegeffekt zurückzuführen: Wenn eine elektromagnetische Welle auf ihre durch Reflexionen und Beugung erzeugte Kopie trifft und sich gegenphasig befindet, heben sich die Wellen gegenseitig auf, dh der Kanal friert sozusagen ein .
Das Fading ist schnell und langsam ( schnelles und langsames Fading).
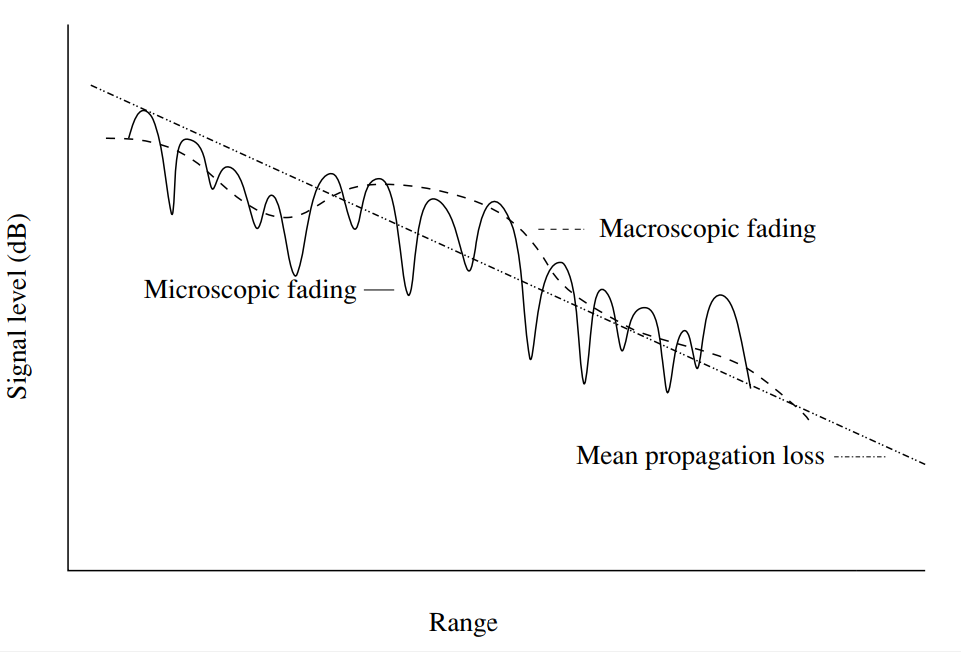
Abb. 1. Schwankungen der Signalleistung in Funkkanälen je nach Entfernung. Der durchschnittliche Ausbreitungsverlust steigt mit zunehmender Reichweite monoton an. Lokale Abweichungen können durch makroskopisches (langsames) und mikroskopisches (schnelles) Ausbleichen auftreten [1, S.14].
Ich gestehe sofort, heute werden wir nicht mit langsamem Fading arbeiten, aber wir werden ausführlich genug über schnelle sprechen.
Abb. 2. Darstellung des Schattierungseffekts: In der Regel tritt aufgrund der Schattierung (Shadowing) ein langsames Ausbleichen auf. Für die Simulation wird normalerweise die logarithmische Normalverteilung gewählt.
Wenn Sie etwas über langsames Fading und darüber, wie Sie Satellitenkanäle im Allgemeinen simulieren können, lesen möchten, lade ich Sie hierher ein !
Schnelles Ausbleichen
Schnelles Ausbleichen tritt in der Regel aus zwei Hauptgründen auf:
- aufgrund der bereits erwähnten Mehrwegeausbreitung und / oder
- aufgrund von Doppler-Frequenzverschiebungen .
Letztere sind für Satellitensysteme sehr auffällig, werden jedoch bei terrestrischer Kommunikation nicht immer berücksichtigt, da die Basisstationen in diesem Fall in der Regel stationär sind.
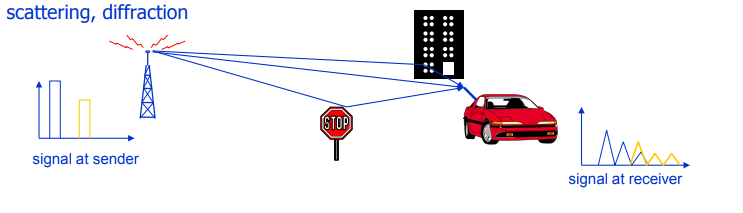
Abb. 3. Darstellung der Ursachen für das Ausbleichen. Besonderes Augenmerk wird auf Streuung und Beugung gelegt: Gerade aufgrund dieser Phänomene entsteht die sogenannte Mehrwegeausbreitung, die zu Intersymbolinterferenz ( ISI ) führt.
Aber das ist noch lange nicht alles.
Selektives Fading vs. Flaches Ausbleichen
Oben haben wir unsere Störung durch die Art des Ereignisses geteilt . Interferenzen können jedoch auch durch die Art der Auswirkung auf das übertragene Signal geteilt werden . Und hier brauchen wir das Konzept der Kanalselektivität .
Wir geben eine kleine Klassifikation nach [1, S. 14-18]. Schnelles Ausbleichen kann also sein:
- Selektiv
a. Frequenzselektiv
b. Zeitselektiv
c. Räumlich selektiv (dies bezieht sich auf das Problem der Ankunfts- und Abflugwinkel von EM-Wellen - heute werden wir dieses Problem nicht analysieren) - Flach - mehr in Richtung der Natur des langsamen Verblassens (ja, das ist so ein Paradoxon)
Was der letzte Begriff impliziert, wird aus dem Gegenteil erklärt.
Erstens, wenn die Breite des Spektrums des von uns übertragenen Signals die kohärente Bandbreite des Kanals überschreitet, dann sagen sie, dass es sich um frequenzselektive Interferenzen handelt.
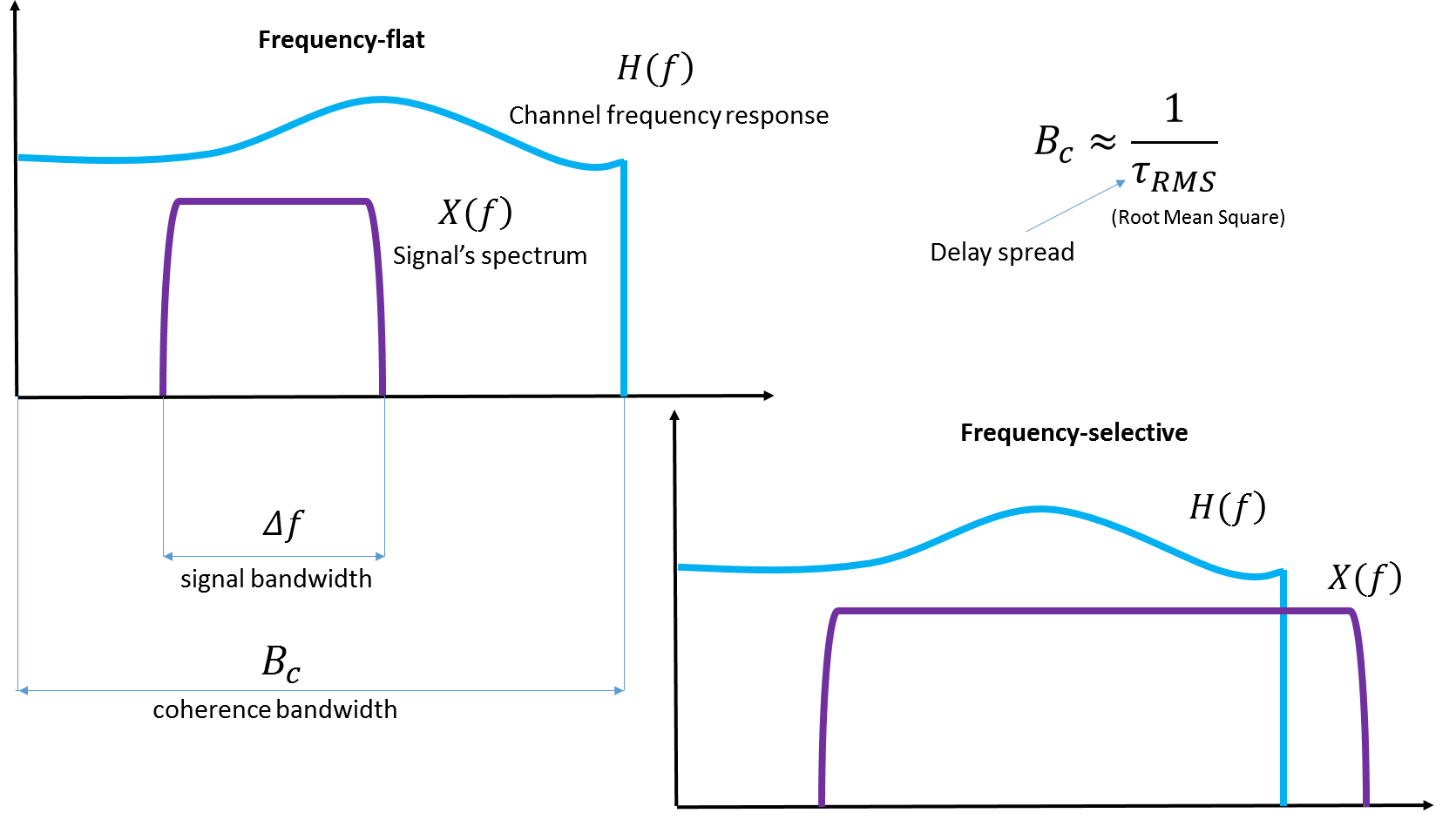
Abb. 4. Darstellung der kohärenten Bandbreite. Ich denke, es wird keine schlechte Idee sein, Illustrationen aus dem Wiki beizufügen, wenn er sie selbst dort hinzufügt.
Achten Sie auf die variable Verzögerungsspanne - die Verteilung der Verzögerungen. Diese Streuung in Verzögerungen zwischen dem Eintreffen verschiedener Kopien desselben Signals wird gemessen, wenn die Eigenschaften eines bestimmten realen Kanals bestimmt werden.
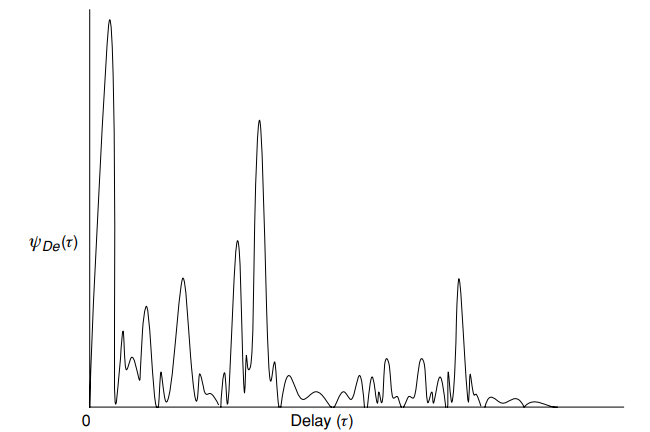
Abb. 5. Typisches Verzögerungsprofil (Leistungsprofil) )
- durchschnittliche Leistung als Funktion der Verzögerung 
[1, S. 16]
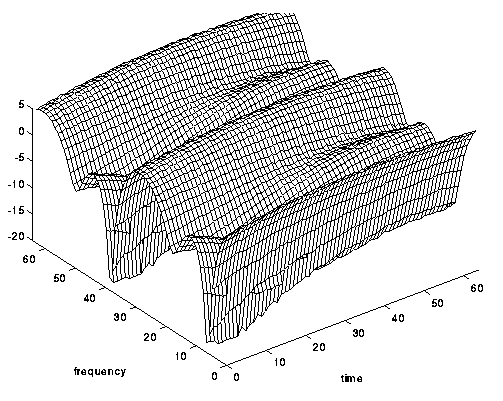
Abb. 6. Frequenzselektiver, aber nicht zeitselektiver Kanal .
Für jeden Bereich ist das kohärente Band unterschiedlich.Zum Beispiel für das S-Band (ich war interessiert, als ich nach Informationen über Satellitensysteme suchte) Bc = 0,5 - 2 MHz (Kanatas AG, Panagopoulos AD (Hrsg.). Funkwellenausbreitung und Kanalmodellierung für Erd - Weltraum - Systeme. - CRC Press, 2016 - S. 107).
Dies passt sehr gut zur Baudrate eines solchen Satelliten-Transceivers . Und es ist nicht überraschend: Die Symbolrate linearer Arten der digitalen Modulation (PSK, QAM, OFDM) stimmt mit dem vom Signal belegten Band überein (siehe Goldsmith A. Wireless Communications . - Stanford University, 2004. - S. 140, 326) Es wäre schön zu versuchen, das Signal maximal in das kohärente Band zu drücken. Frequenzen sind immer noch eine wertvolle Ressource.
Zweitens, wenn die Länge unseres Signals im Zeitbereich die Kanalkohärenzzeit überschreitet, heißt es, dass es sich um einen Kanal handelt, der zeitlich variiert.
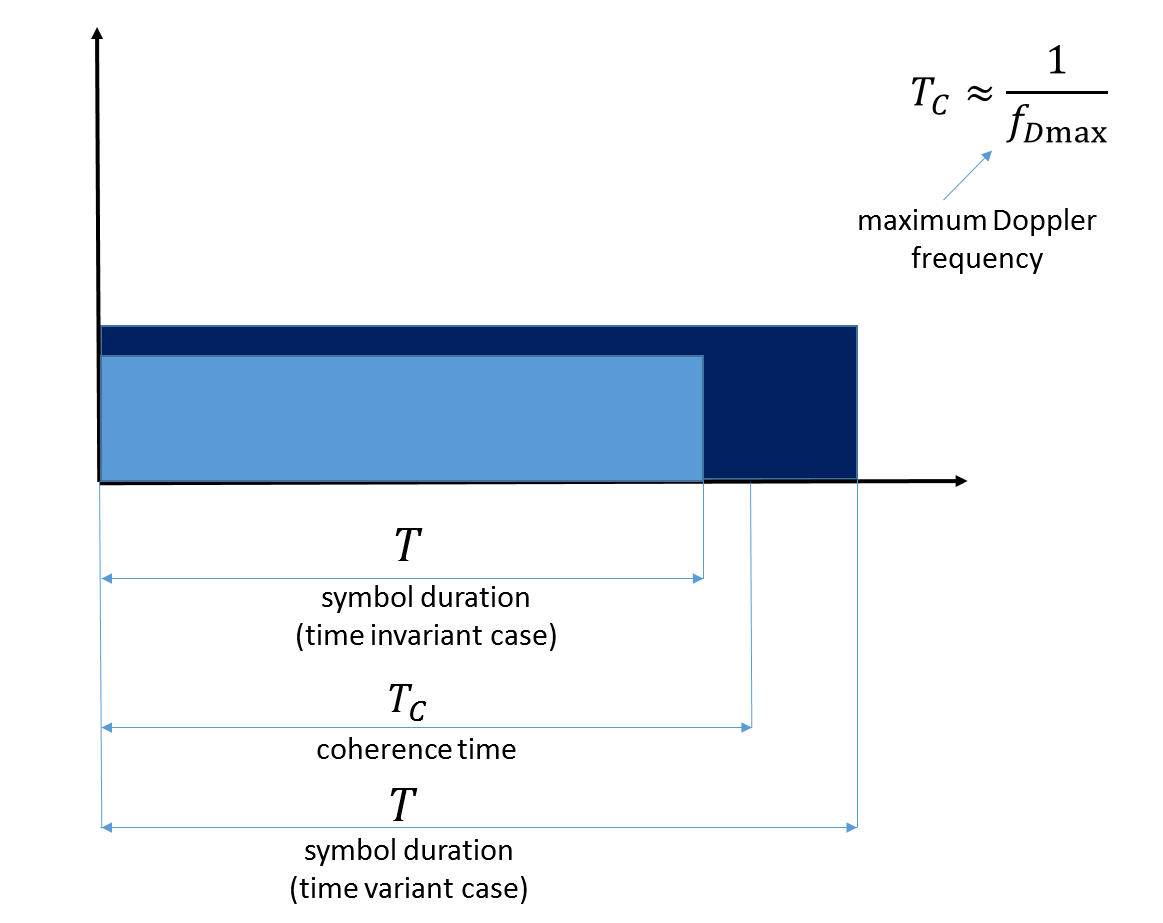
Abb. 7. Darstellung der Kohärenzzeit. Bitte beachten Sie, dass hier die maximale Dopplerfrequenz die Bewegung des mobilen Endgeräts selbst widerspiegelt.
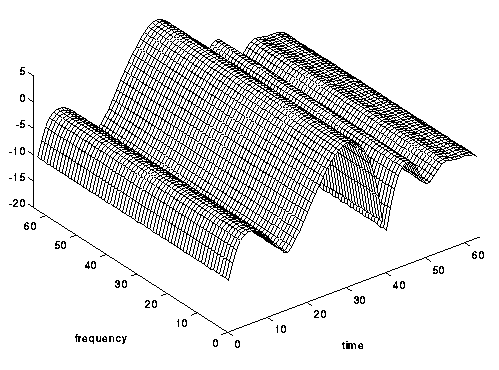
Abb. 8. Fast zeitlich unsichtbar, aber zeitselektiv: ein schnell abfallender Kanal.
Im wirklichen Leben muss man leider beides erwarten. Nun, und dementsprechend, wenn wir es irgendwie schaffen, das Obige zu vermeiden, werden wir zum einfachsten und bequemsten Fall kommen - Flat Fading [1, S. 14-18] [2, p. 88-92].
Der einfachste Fading-Kanal
Möglicherweise haben Sie bereits einen ähnlichen Weg gesehen, um einen flachen Kanal mit irgendwo verblassendem Bild zu simulieren:
h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg)))
Was ist gemeint:
- mangelnde Sichtverbindung (ein Fall, der für die terrestrische Kommunikation gerechtfertigt ist)
- Schmalbandkanal (Schmalbandkanal) - passt in das kohärente Band
- Es gibt auch keine Frequenzselektivität - passt in die kohärente Zeit
- fehlende Schattierung und Doppler-Frequenzverschiebungen
Das heißt, hier ist es persönlich: ein flacher Kanal mit Verblassen . Für einen Fall ohne Sichtlinie wird der Kanal auch Rayleigh genannt .
Lord Rayleigh
Woher kommt ein solches Modell?
Wenn wir über moderne Kommunikationssysteme sprechen, meinen wir höchstwahrscheinlich die Arbeit mit digitalen Signalen. Darüber hinaus arbeiten wir höchstwahrscheinlich auch mit Quadraturmodulationstypen ( I / Q ), dh mit komplexen Signalen.
Abb. 9. Die Signalkonstellation QPSK . Polarkoordinaten, Einheitskreis. Beispielsweise entspricht das Symbol 11 einer Koordinate, die ungefähr 0,7 + 0,7i entspricht .
Es ist logisch, die Auswirkung von Interferenzen sowohl auf die reale als auch auf die imaginäre Komponente anzunehmen. Darüber hinaus lohnt es sich, dem zentralen Grenzwertsatz zu folgen, um auch die Gaußsche Natur solcher Effekte anzunehmen. Wir schreiben die Formel [1, S. 39]:
wo )
und )
Sind normalverteilte Zufallsvariablen.
Am häufigsten wird ein Modell mit einer normalisierten Durchschnittsleistung verwendet:
Und das heißt )
.
Wenn wir unabhängige Verzerrungen der Komponenten der Signalhüllkurve annehmen: sowohl in Phase ( I - In Phase) als auch Quadratur ( Q - Quadratur), dann kann die Position der Zahl, mit der das ursprüngliche Symbol multipliziert wird (daher das multiplikative Rauschen), in Polarkoordinaten angegeben werden wörtlich berechnet nach dem Satz von Pythagoras:
wo )
und )
- Dies sind auch normalverteilte Zufallsvariablen. Für Nennleistung )
, )
.
Und hier haben wir die Formel des Rayleigh-Prozesses ! [2, S. 78]
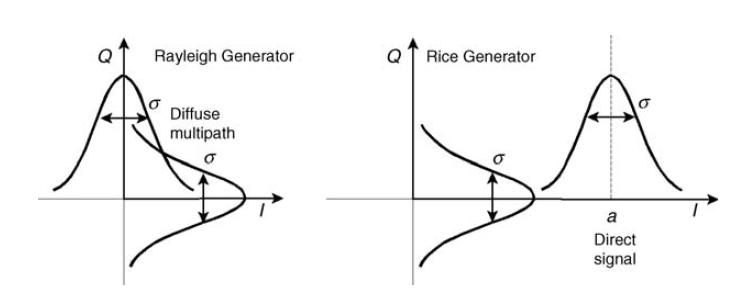
Abb. 10. Gaußsche Quadratgeneratoren zur Modellierung des Verblassens von Rayleigh und Reis [3, S.125]. Wir werden etwas später über den Reiskanal sprechen.
Lyrischer Exkurs.Persönlich mag ich das Beispiel der Waffensichtung sehr : Wenn zwei Kanonen ausreichend oft senkrecht zueinander schießen, ist die Verteilung der Treffer für jede einzelne normal und die Gesamtverteilung der Treffer ist Rayleigh. Ähnliches passiert mit unserer Einmischung.
Wenn wir den einfachsten Fall ohne räumliche Korrelation zwischen den Kanälen betrachten (sagen wir, wir haben mehrere räumliche Kanäle - MIMO ), dann sagen sie, dass der Kanal räumlich weiß ist - räumlich weiß . Und da alle Kanäle unabhängig sind, können nicht nur Zufallsvariablen, die nach Rayleigh verteilt sind, sondern auch Vektoren, Matrizen und Tensoren „erzeugt“ werden [3, S. 125]:
wo %20)
und %20)
Sind Matrizen, die aus normalverteilten Werten bestehen?
Woher kam 1/2 unter der Wurzel?Hier ist alles ganz einfach: Wie oben erwähnt, sollte die Kanalantwortleistung gleich Eins sein, d.h.
Hierzu wird der Skalierungsfaktor eingeführt 
.
Demonstrieren (zur Abwechslung Python nehmen):
import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)
Zusammenfassend :
Die Interferenzkomponente ohne direkte Sichtbarkeit kann als n-dimensionaler Vektor (abhängig von der Kanaldimension) unabhängig identisch verteilt ( IID - unabhängig identisch verteilt) gemäß dem komplexen Gaußschen Gesetz mit Kreissymmetrie und Nullmatte beschrieben werden. Erwartungszahlen ( ZMCSCG - zirkular symmetrische komplexe Gaußsche Zahlen mit dem Mittelwert Null).
Ein ganzer Zungenbrecher!
Fast der einfachste Fading-Kanal
Was ist, wenn es immer noch direkte Sicht gibt? Vielleicht gibt es in dieser Hinsicht bereits vorgefertigte mathematische Modelle?
Natürlich gibt es! Zum Beispiel dies [4] , verallgemeinert für den Fall mit mehreren Empfangs- und Sendeantennen (MIMO):
wo 
- Dies ist eigentlich die komplexe Hüllkurve der Impulsantwort des Kanals (oder der Kanalmatrix, wenn es sich um MIMO handelt ). 
Ist eine Komponente der direkten Sichtbarkeit (Sichtlinie) und 
- Dies ist eine Komponente des Mangels an direkter Sichtbarkeit (Non-Line-of-Sight), wir haben dies bereits berücksichtigt.
Beachten Sie die Variable K - dies ist der sogenannte Ricean-Faktor (Rician / Ricean-Faktor) - das Verhältnis der Leistung des direkten Ausbreitungspfads zur Leistung aller anderen Pfade. Er bestimmt, wie stark unser Kanal gestört wird.
Stephen O. "Steve" Rice
Laufzeit 
stellt die mathematische Erwartung der Kanalmatrix dar und kann basierend auf der Geometrie der Empfangs- und Sendearrays von Antennen modelliert werden:
wo )
und )
- Dies sind die Antworten der Empfangs- und Sendearrays von Antennen und 
und 
Sind die An- und Abflugwinkel (Abflugwinkel).
Die Faktoren sind im Allgemeinen symmetrisch und können durch die allgemeine Formel beschrieben werden:
wo 
Ist der Abstand zwischen Antennen (Antennenabstand) in Wellenlängen und 
- Dies ist die Anzahl der Elemente in der Antennenanordnung (Abb. 11).
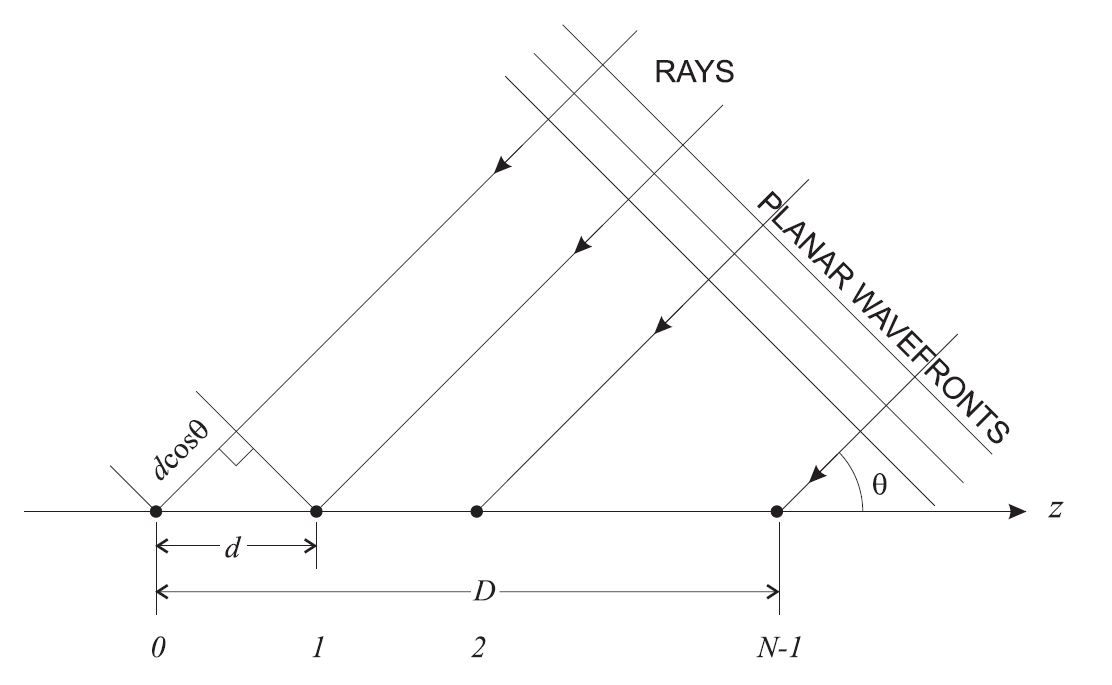
Abb. 11. Die Geometrie eines linearen Arrays . Für Massive MIMO wird die Geometrie natürlich anders sein. Mehr dazu lesen Sie zum Beispiel hier .
Nun, da das Modell zumindest etwas zerlegt ist, können Sie es vereinfachen.
Für den Fall von SISO (dem einfachsten und grundlegendsten) hat Formel (5) die Form:
für 1 Sende- und 1 Empfangsantenne %5Cmathbf%7Ba%7D_R(%5Ctheta_R)%20%3D%201)
.
Und das passt übrigens zum Modell in Abbildung 12.
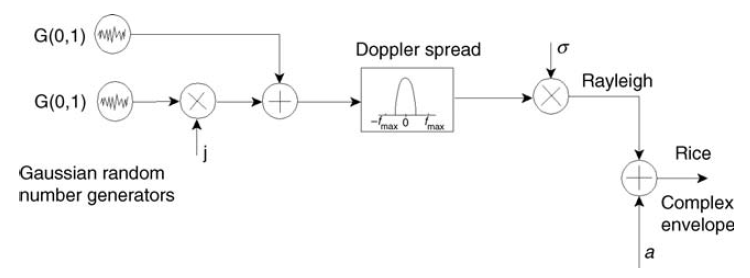
Abb. 12. Das Schema der Bildung des Reiskanals (Schmalbandsignal) [3, S.127]. Bei 
Der Kanal wird immer mehr in Rayleigh ausarten. Deshalb habe ich das Wort fast im Untertitel verwendet: Der Rayleigh-Kanal ist ein Sonderfall des Rice-Kanals. Dies ist auch aus Formel (5) ersichtlich.
Lassen Sie uns erklären: %7D%7D)
Ist der Rician-Skalenparameter und 
Ist ein Nicht-Zentralitätsparameter.
Wenn wir ein flaches Fading betrachten, wird angenommen, dass der Doppler-Spread-Block eine Antwort von 1 hat.Im Allgemeinen werden Sie zum Modellieren der Doppler-Ausbreitung höchstwahrscheinlich auf ein Jakes-Modell (U-Form) stoßen, das auf der Sum-of-Sinusoids-Technik basiert. Theoretisch sieht das Spektrum eines solchen Modells folgendermaßen aus:
Die Leistungsspektraldichte der Rayleigh-Dämpfung bei einer maximalen Doppler-Verschiebung von 10 Hz. Quelle
Im Leben jedoch nach [1, S. 15] ein solches Spektrum sieht noch weniger gleichmäßig aus:
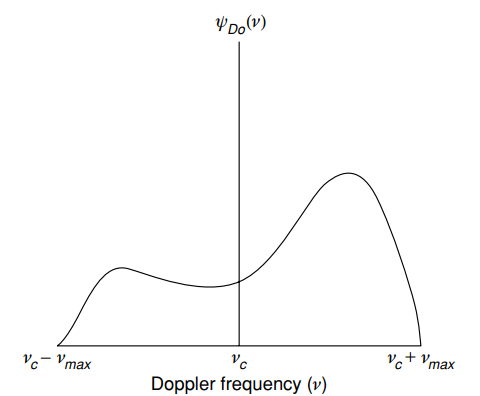
Typisches Doppler (Energie) Spektrum )
- Durchschnittsleistung als Funktion der Dopplerfrequenz )
[1, S. 15].
Erwartungen ... Realität.
Es gibt solche Schemata zum Kombinieren mit langsamem Fading.Dies gilt beispielsweise für das Corazza-Vatalaro-Modell (C & V) :
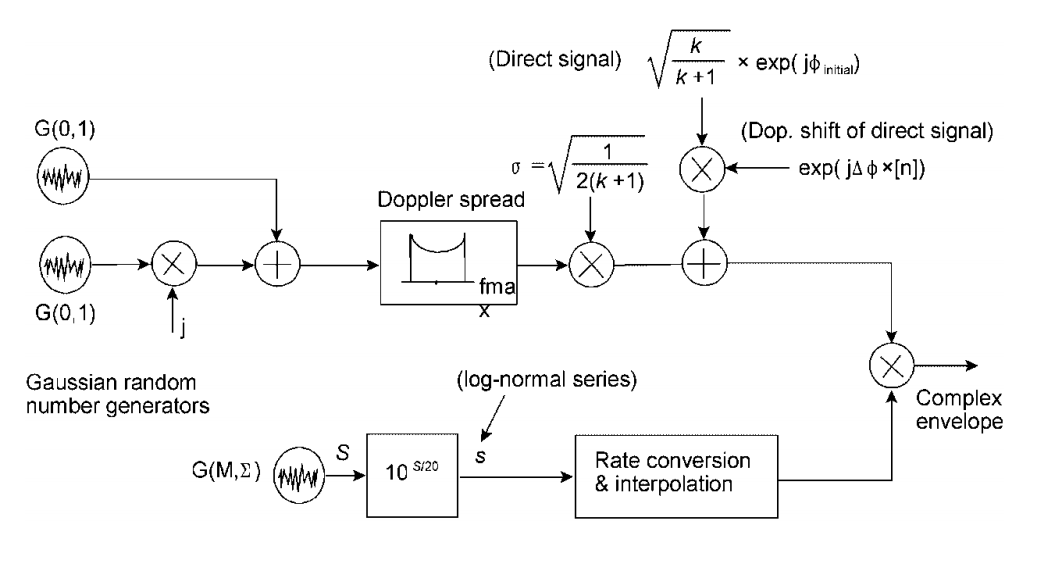
siehe Fontan, FP, Mayo, A., Marote, D., Prieto-Cerdeira, R., Mariño, P., Machado, F. & Riera, N. (2008). Überprüfung generativer Modelle für den mobilen Breitband-Satelliten-Ausbreitungskanal. Internationale Zeitschrift für Satellitenkommunikation und -vernetzung, 26 (4), 291-316.
Aber das ist eine ganz andere Geschichte ...
Modellierung des fast einfachsten Fading-Kanals in MatLab
Vergleichen wir die erhaltenen Berechnungen mit etwas, das bereits überprüft wurde. Zum Beispiel mit speziellen MatLab-Funktionen .
Um das Modell zu testen, generieren wir unsererseits eine zufällige binäre Nachricht (die Nachrichtenlänge beträgt 100.000 Bit), modulieren sie mit M-PSK oder M-QAM , multiplizieren den Fading-Prozess Element für Element, fügen weißes Gaußsches Rauschen hinzu, gleichen den Zero-Forcing-Equalizer aus, demodulieren und berechnen Bitfehlerverhältnis (BER - Bitfehlerverhältnis) (Abb. 13). Die Anzahl der Tests beträgt einhundert.
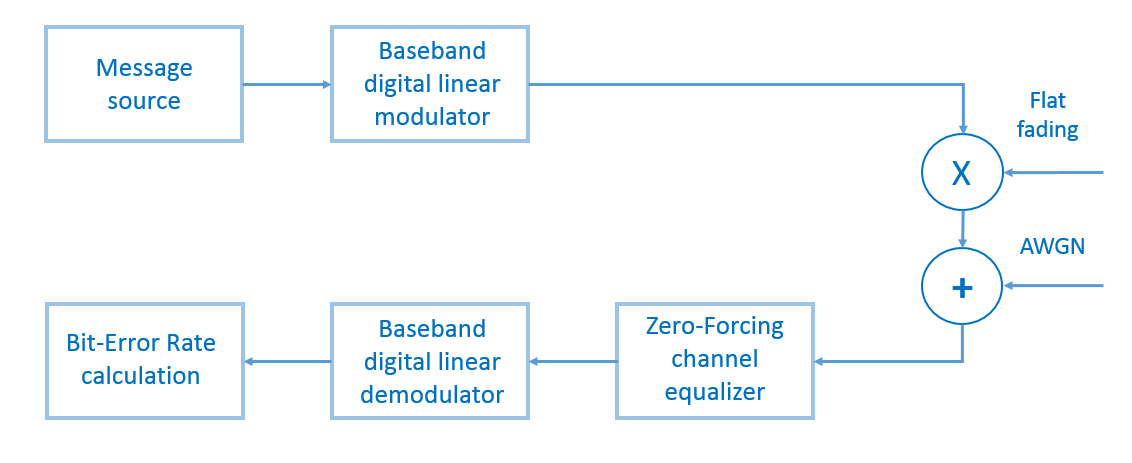
Abb. 13. Das Blockdiagramm des Modells des Übertragungssystems, das in unserem Skript beschrieben wird.
Das Skript kann hier eingesehen werden.Und hier herunterladen.
clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256];
Sie sollten so etwas bekommen:
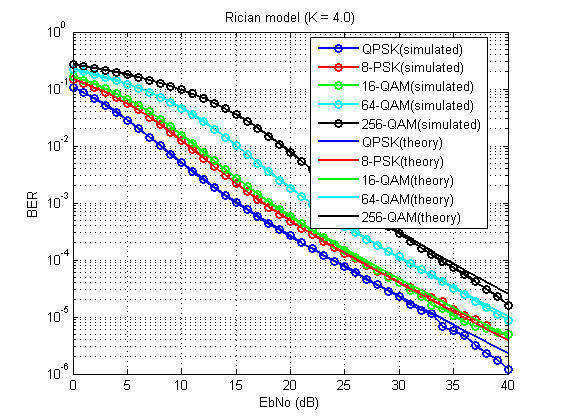
Abb. 14. Der Bitfehlerkoeffizient für das betrachtete Modell (K = 4,0).
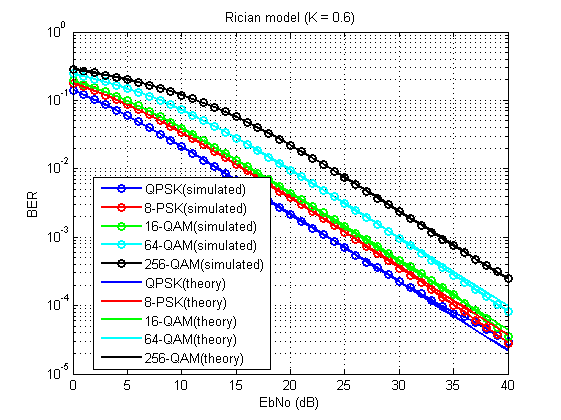
Abb. 15. Bitfehlerrate für das betrachtete Modell (K = 0,6).
Natürlich nicht ohne Mängel (aufgrund der begrenzten Anzahl von Durchschnittswerten), aber im Allgemeinen kann man sehen, dass es funktioniert!
Ok, aber wird es möglich sein, das Experiment auf den Fall von MIMO zu skalieren? Ja natürlich.Dazu nehmen wir eine Annahme an: Die Kanalmatrix besteht aus unabhängigen Ausbreitungspfaden, von denen jeder nach Rice verteilt wird.
Unter welchen Bedingungen ist das möglich?
Wie oben erwähnt, kann die Komponente IID in jeder Dimension erzeugt werden. Dies bedeutet, dass jeder räumlich weiße MIMO-Kanal ohne Sichtlinie als Satz von SISO-Kanälen modelliert werden kann (abhängig von der Kanalabmessung).
Da die Sichtlinienkomponente etwas komplizierter ist, müssen Sie die Position der Gitter berücksichtigen.
Betrachten Sie die Formel (5): Wenn unsere Matrix der Sichtlinienkomponente nur aus Einheiten besteht 
scheint es, dass die Raysov-Komponente auch räumlich weiß wird.
Um dies zu erreichen, schreiben wir die Sichtlinienkomponente detaillierter auf als in Formel (6):
)%20%20%5C%5C%0A.%20%5C%5C%0A.%20%5C%5C%0A.%5C%5C%0A%5Cexp(j(M_R-1)2%5Cpi%20dcos(%5Ctheta_R))%0A%5Cend%7Bbmatrix%7D%20%5Cbegin%7Bbmatrix%7D%20%0A1%20%26%20%5Cexp(j2%5Cpi%20dcos(%5Ctheta_T))%20%20%26%20.%20%26%20.%20%26%20.%20%26%0A%5Cexp(j(M_T-1)2%5Cpi%20dcos(%5Ctheta_T))%0A%5Cend%7Bbmatrix%7D%0A)
Es fällt auf, dass wenn 
dann besteht die Matrix aus einer Einheit. Geometrisch ist dies eine Situation, in der zwei Arrays von Elementen streng aufeinander ausgerichtet sind:
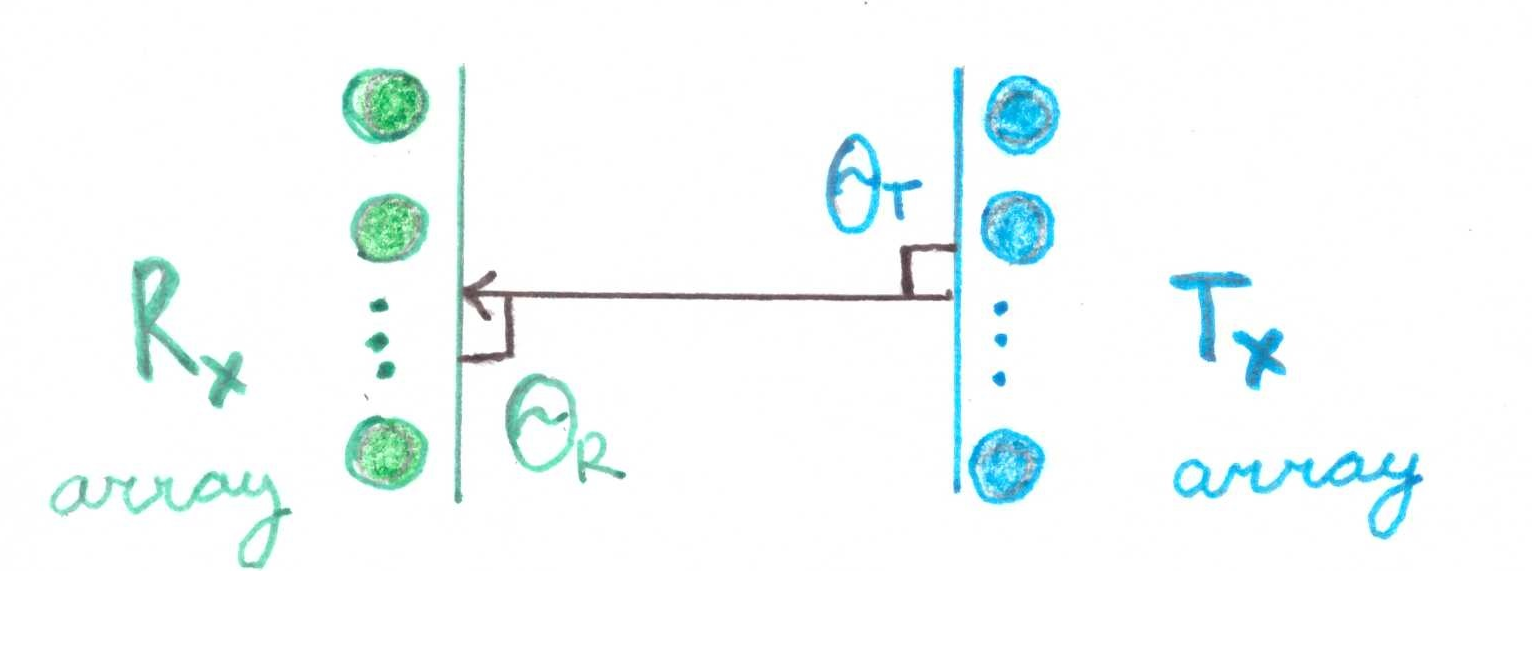
Lassen Sie uns eine kleine Mathe-Demonstration machen:
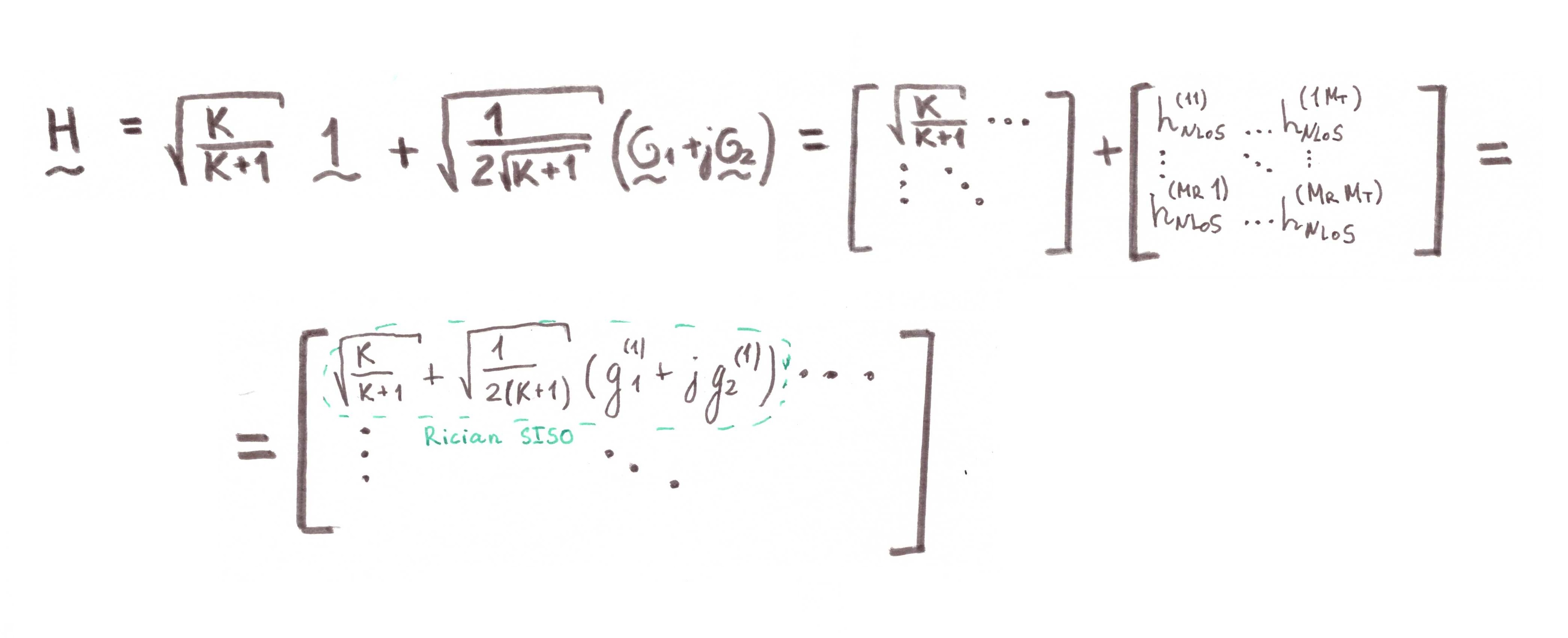
Für die Modellierung verwenden wir das Alamouti-Schema . Es sollte sich ungefähr so herausstellen:
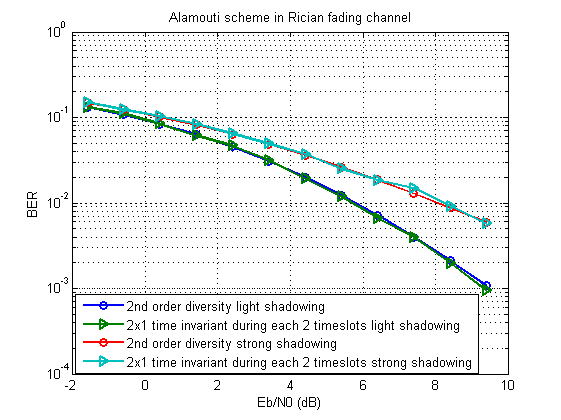
Das erweiterte Skript kann hier heruntergeladen werden .
Gut gemacht.
Fast der einfachste Fading-Kanal und räumliche Korrelation
Und jetzt, nachdem wir unsere Reise in die Welt der statistischen Berechnungen abgeschlossen haben, kommen wir der Realität ein wenig näher.
Oben haben wir den Fall betrachtet, in dem die Komponente des Mangels an Sichtlinie räumlich weiß war . Von realen Systemen sollte man jedoch immer noch eine gewisse Korrelation zwischen den Antennen und daher zwischen den Ausbreitungswegen der EM-Welle erwarten.
Wir führen eine neue Variable ein - die räumliche Korrelationsmatrix:
wobei vec eine Vektorisierungsoperation bezeichnet . Diese Matrix wirkt sich übrigens nur auf die Komponente des Mangels an Sichtlinie aus , und daher in diesem Fall 
.
Es ist anzunehmen, dass diese Matrix im wirklichen Leben zuerst durch Messungen bestimmt wird und erst dann zur Modellierung verwendet wird:
wo 
Ist die IID-Matrix ( w bedeutet räumlich weiß).
Beachten Sie, dass das Erhöhen einer Matrix auf eine Potenz nicht das Erhöhen auf eine Potenz jedes ihrer Elemente ist. Daher kann in unserem Fall die Funktion sqrt () in MatLab nicht verwendet werden. Verwenden Sie den Operator ^ .
Im Fall von Python können Sie den Exponentiationsoperator ** und die sqrt-Methode des beliebten numpy- Moduls nicht verwenden. Sie müssen die fraktional_matrix_power- Methode des scipy- Moduls verwenden.
Wenn Empfänger und Sender wie in Abbildung 16 ausreichend unabhängig voneinander sind, kann das Kronecker-Modell angewendet werden [1, S. 40], um die Anzahl der zu berechnenden Koeffizienten zu verringern:
wo 
bezeichnet eine Kronecker-Arbeit .
Leopold Kronecker
Wir betrachten die Komponenten der Ausdrucksmatrix separat:
%5ET%5Cright%5C%7D)
Ist die Korrelationsmatrix der Empfangsantennen,
Ist die Korrelationsmatrix der Sendeantennen
und 
- Dies ist die Anzahl der Empfangs- und Sendeantennen. Beide Matrizen sind positive semi-definitive hermitische Matrizen. Darüber hinaus ist der Rang der Matrix 
durch den Wert begrenzt %2C%20rank(%5Cmathbf%7BR%7D_R)))
.
Abb. 16.
Modell der Diffusoren bei nicht korrelierendem Empfänger und Sender. Grüne Punkte bedeuten Diffusoren, blaue und rote bedeuten Empfänger und Sender. Ich entschuldige mich für die Qualität, dies ist ein Screenshot einer Hausaufgabe der TU Ilmenau.
Die Kanalmatrix kann in diesem Fall wie folgt geschrieben werden:
In Situationen wie beispielsweise in Abbildung 17 müssen Sie jedoch weiterhin die vollständige Korrelationsmatrix verwenden (siehe Formel (9)).
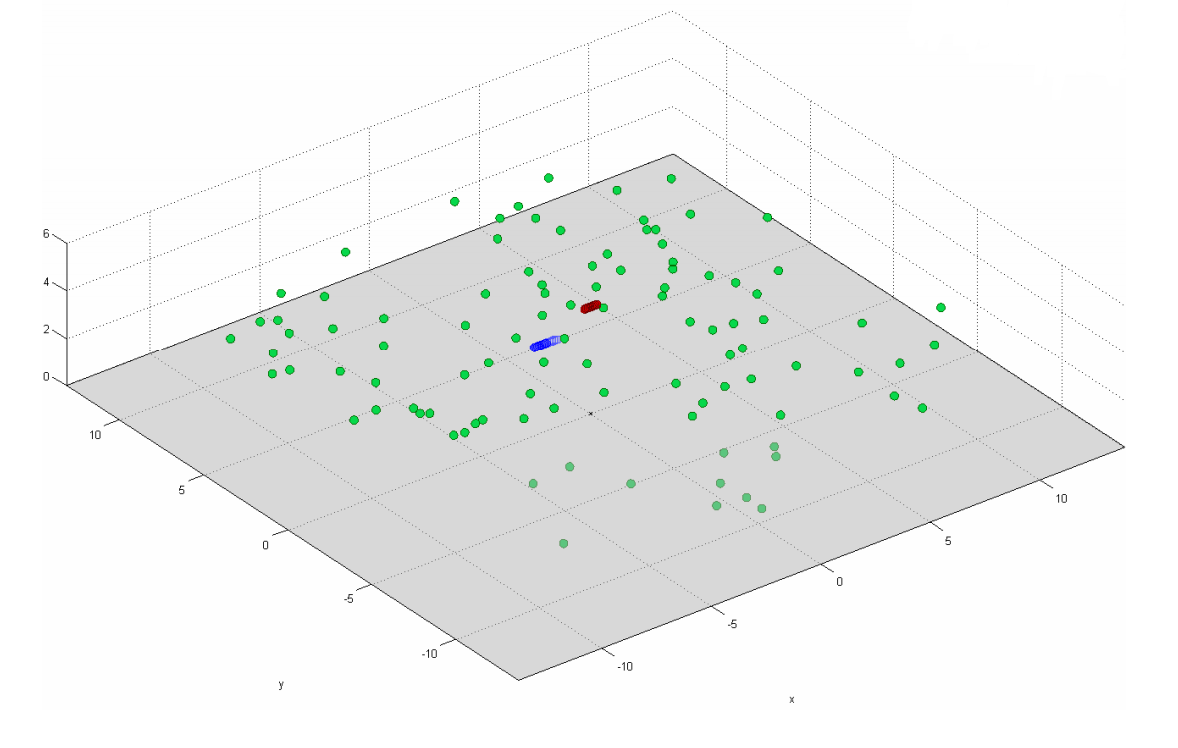
Abb. 17. Modell der Diffusoren bei Korrelation von Empfänger und Sender. Grüne Punkte bedeuten Diffusoren, blaue und rote bedeuten Empfänger und Sender.
Um das Gelernte zu konsolidieren und zu sehen, wie räumliche Korrelation das Leben kompliziert, versuchen wir, die Bandbreite der Kanäle zu berechnen. Zum Beispiel für MIMO 2x2.
Dazu nehmen wir die folgenden Fälle (wir meinen alle das gleiche flache Fading, der Einfachheit halber betrachten wir auch nur den Rayleigh-Kanal):
1) räumlich weißer Kanal;
2) Kronecker-Modell mit einer relativ schwachen Korrelation:
3) Kronecker-Modell mit relativ starker Korrelation:
In diesem Teil werden wir Python 3.4 verwenden . Die Funktion zur Berechnung der Bandbreite stammt aus einer meiner früheren Veröffentlichungen .
import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)
Definieren Sie die Hauptparameter des Systems:
Mr = 2
Wir starten die Simulation:
counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)
Zeichnen plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()
Wir bekommen:
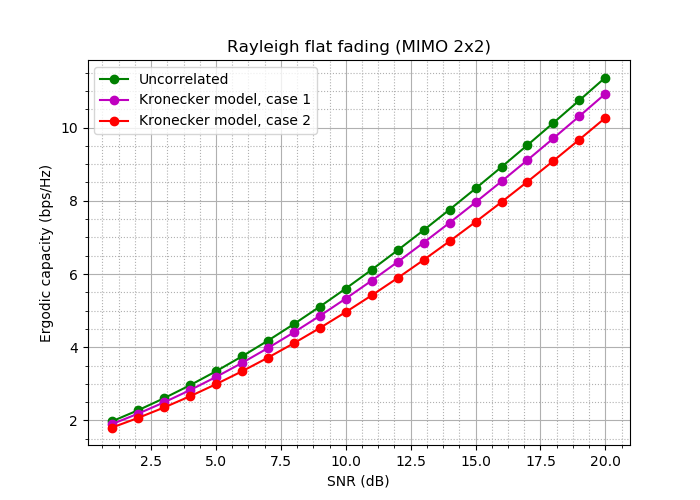
Abb. 18. Bandbreitenkurven für diese Experimente.
Nun, der Unterschied ist zwar nicht kritisch, aber!
Nachwort
Vielleicht hat einer der Leser bemerkt, dass fast alles, was wir heute (im Detail und im Vorbeigehen) untersucht haben, ziemlich gut mit den Parametern des Matlab-Objekts comm.MIMOChannel übereinstimmt . Diese Tatsache scheint mir sehr wichtig zu sein:
- Erstens systematisiert es das oben Beschriebene weiter.
- und zweitens wird betont, dass wir uns mit aktuellen Themen befassen.
Nun, und jetzt, wenn Sie solche Blöcke verwenden, wird hoffentlich klarer, warum und welche Stifte Sie drehen müssen.
Vielen Dank für Ihre Aufmerksamkeit!
PS
Ich werde hier einen Link zu den Folien zum Thema von Reiner S. Thomä (Ilmenau) hinzufügen, zu denen er uns damals Vorträge gehalten hat. Ich denke, jemand wird sich als nützlich erweisen!
Literatur
- Paulraj, Arogyaswami, Rohit Nabar und Dhananjay Gore. Einführung in die drahtlose Raum-Zeit-Kommunikation. Cambridge University Press, 2003.
- Goldschmied A. Drahtlose Kommunikation. - Cambridge University Press, 2005.
- Fontæn, Fernando Pærez und Perfecto Mariæo Espiæeira. Modellierung des drahtlosen Ausbreitungskanals: Ein Simulationsansatz mit Matlab. Vol. 5. John Wiley & Sons, 2008.
- Farrokhi, Farrokh R. et al. "Spektrale Effizienz von FDMA / TDMA-Funksystemen mit Sende- und Empfangsantennenarrays." IEEE-Transaktionen zur drahtlosen Kommunikation 1.4 (2002): 591-599.