Fraktale in irrationalen Zahlen. Teil 2

Teil 0: Fraktale in Primzahlen.
Teil 1: Fraktale in irrationalen Zahlen.



Der Artikel enthält Gif und kontrastierende Bilder. Epileptiker können einen epileptischen Anfall haben.

In einem früheren Artikel haben wir uns einen Algorithmus zur Visualisierung von Binärsequenzen angesehen. Erinnern wir uns.

Nehmen Sie die binäre Sequenz. Als Beispiel die ersten Bits einer fraktalen Sequenz, die in einem vorherigen Artikel besprochen wurden:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

0100110110010011001001101100

Wir zeichnen ein quadratisches Zellenfeld. Wir setzen die Bits an der oberen Grenze. Der Abstand zwischen den Bits beträgt zwei Zellen:



Zeichnen Sie für jedes Bit einen gestrichelten Pfad entlang der Diagonale (durch die Zelle). Zeichnen Sie für Nullen den ersten Strich nach rechts:



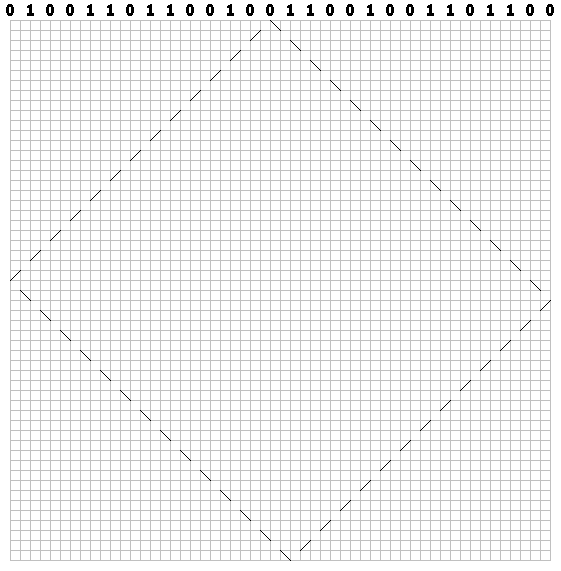
Für Einheiten - links:



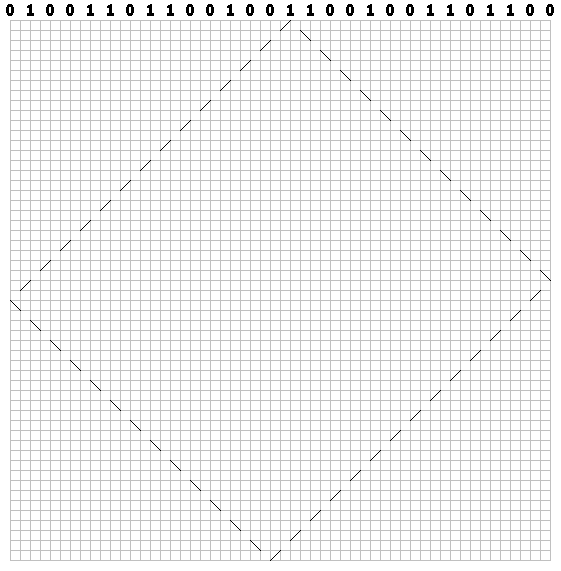
Zeichnen Sie für jedes Bit eine Flugbahn. Wir haben ein Billardmuster:



Ein identisches Muster (ohne diagonalen Defekt - die Sequenz ist unendlich, wir haben sie als endgültige Sequenz visualisiert) kann auf andere Weise erhalten werden. Invertiere jedes gerade Bit in der Sequenz:

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

Zeichnen Sie als nächstes für jedes Bit vertikale gestrichelte Linien:



Wir setzen die Bits links, zeichnen horizontale Linien:



Wir kombinieren:



Nach dem Schreiben des ersten Artikels blieben zwei Fragen ungelöst:

1. Ist es möglich, ein fraktales Muster für irrationale Zahlen zu zeichnen? Du kannst. Das Problem wurde in einem früheren Artikel behoben. Im Bild oben - Teil des fraktalen Musters für $$$\ sqrt {2}$ . Wenn Sie eine der Kurven in diesem Muster auswählen:



Holen Sie sich die bekannte fraktale Kurve - "Fibonacci Wort fraktal".

2. Die zweite Frage ist, ob es möglich ist, einen Algorithmus zu schreiben, der ein Muster malt:



Das zweite Problem wird in diesem Artikel behandelt. Wir werden die Muster mit Hilfe eines Webstuhls färben, dessen Arbeit wir mit JavaScript simulieren.



In der Abbildung oben - die einfachste Maschine. Es besteht aus zwei Rahmen, durch die die Fäden gespannt werden. Die Rahmen sind mit den Pedalen verbunden. Wenn Sie eines der Pedale drücken, steigt einer der Rahmen an. Die durch diesen Rahmen gezogenen Gewinde steigen an und ein Quergewinde wird in den resultierenden Spalt zwischen den Gewinden gespannt. Wenn Sie die geraden und ungeraden Fäden durch verschiedene Rahmen strecken, erhalten Sie eine Bindung in einem Schachbrettmuster:



In komplexeren Maschinen werden vier oder mehr Rahmen verwendet:


Ashford 4 Shaft Tischwebstuhl

Um nicht zu verwechseln, welches Pedal zu drücken ist, erstellen sie ein Diagramm.



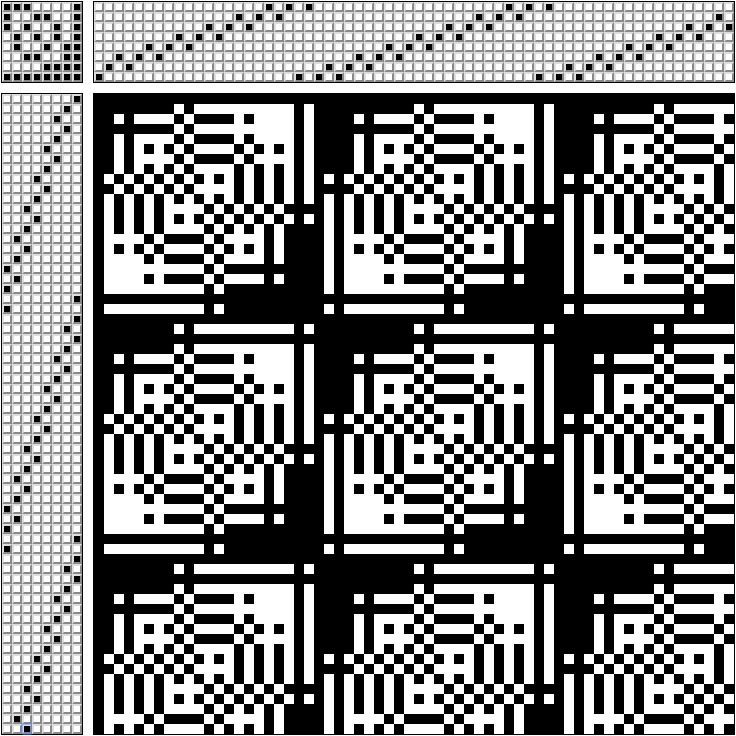
Im oberen rechten Teil des Musters wird angegeben, durch welche Rahmen die Fäden verlaufen (Muster für einen Webstuhl mit 8 Rahmen).

In der oberen linken Ecke - welche Pedale gleichzeitig geklemmt werden sollen (jedes Pedal ist nur mit einem eigenen Rahmen verbunden).

Im unteren linken Teil - in welcher Reihenfolge zu treten.

Im unteren rechten Teil - was für ein Gewebe bekommen wir. Wenn Sie den weißen Faden durch den schwarzen ziehen, erhalten Sie ein monochromes Muster.

Das Prinzip sofort zu „betreten“ mag ein wenig schwierig erscheinen. Das Bild unten zeigt, wie das Webmuster entsteht:



Lassen Sie uns ein Skript schreiben. Wir werden die Fäden mit dem eindimensionalen Array array2 durch die Frames strecken. In das eindimensionale Array Array1 schreiben wir die Sequenz der Pedalklemmung. In Array3 (8x8-Binärarray) schreiben wir, welche Pedale gleichzeitig geklemmt werden sollen.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

Skript (funktioniert in Google Chrome).

Mit Hilfe unseres improvisierten Webstuhls können wir eine Vielzahl von Mustern zeichnen:



Aber historisch gesehen hat die durchschnittliche Person nicht mehr als zwei Beine. Daher ist es zweckmäßig, nicht mehr als zwei Pedale gleichzeitig zu klemmen. Eines der beliebtesten Muster für einen Webstuhl ist wie folgt:



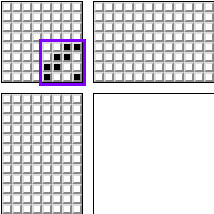
Für 4 Frames. Und seine Modifikation für 8 Frames:



Unerwarteterweise ähneln Muster (oder ein Fragment von Mustern), die mit dieser Vorlage erstellt wurden, unseren „Billard“ -Mustern. Außerdem sind diese Muster schattiert:



Sie können lernen, „Billard“ -Muster für einen Webstuhl auszuwählen. Ein Beispiel:



Zu Beginn des Artikels haben wir bereits ein Fragment dieses Musters gesehen.

Beenden Sie mit Webstühlen und schreiben Sie ein Skript, um binäre Sequenzen zu visualisieren. Wir können eines der Arrays loswerden - das Muster ist diagonal symmetrisch. Wie fülle ich das verbleibende Array? Grundstufe:



Wir nehmen die Sequenz für $$$\ sqrt {2}$ . Erstellen Sie ein Array. Schreiben Sie in das Nullelement des Arrays das Nullbit der Sequenz. Nehmen Sie alternativ jedes Bit der Sequenz. Wenn das n-te Bit = 1 ist, schreiben Sie in das Array a [n] = a [n-1] +1. Wenn bit = 0 - schreibe a [n] = a [n-1] -1

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ... \\ a_n = \ begin {Fälle} a_ {n-1} +1, Q_n = 1; \\ a_ {n-1} -1, Q_n = 0 \ end { Fälle}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

Wir prüfen:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

Tatsächlich haben wir bereits ein elementares Fraktal erhalten, aber wir werden weitermachen.

Als nächstes werden wir uns mit der Matrix befassen:



Fassen Sie zusammen $$$x$ und $$$y$ . Teilen Sie Modulo durch 4. Wenn das resultierende Ergebnis = 0 oder 1 ist - schreiben Sie in die Matrix true. Schreiben Sie für 2 und 3 false. Wir können auf eine Matrix verzichten (es ist nicht im Voraus bekannt, welche Maximal- und Minimalwerte ein [n] annimmt). Fassen Sie a [x] und a [y] zusammen. Fügen Sie dem resultierenden Betrag eine Zahl hinzu $$$C$ (um diese Fälle loszuwerden, wenn der Betrag eine negative Zahl ist). Teilen Sie Modulo durch 4. Malen Sie für die Werte 0 und 1 das Pixel mit Koordinaten über $$$x$ und $$$y$ .

Der endgültige Algorithmus benötigt nur wenige Zeilen:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

Visualisieren Sie unsere fraktalen Sequenzen.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Sie können das Skript leicht ändern, um ein RGB-Bild zu erhalten:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

Oben haben wir der Summe a [x] + a [y] eine Zahl hinzugefügt. $$$C$ . Wenn Sie diese Zahl nicht addieren, ist der Minimalwert der Summe = -8, der Maximalwert = 8 (für $$$x$ und $$$y$ von 0 bis 750). Wenn Sie entfernen $$$C$ - In einigen Fällen ist die Summe negativ und kein Vielfaches der 4. und in diesen Fällen wird das Pixel nicht übermalt (bleibt schwarz):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

Sie können sich vorstellen, dass sich ein Teil des Fraktals unterhalb einer imaginären Grenze befindet (unterhalb dieser Grenze sind nur negative Werte Vielfache von 4: -4, -8, -12, ...).

Wir können sehen, wo diese Grenze ist:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

Anstatt Modulo zu teilen, können wir die Summe mit einem bestimmten Wert vergleichen und dabei nur eine „Schicht“ des Fraktals übermalen. Nehmen Sie als Beispiel den Durchschnitt zwischen dem Minimal- und dem Maximalwert:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

Wenn Sie die Werte von Minimum auf Maximum ändern, können Sie sehen, wie sich die "Ebenen" in der Dynamik ändern:




Außerdem können wir „auf der Stirn“ ein [x] mit einem [y] vergleichen und auch ein fraktales Muster erhalten:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

Die folgende Reihenfolge:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Mittlere Schicht:



In der Dynamik:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Mittlere Schicht:



In der Dynamik:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Mittlere Schicht:



In der Dynamik:

$$

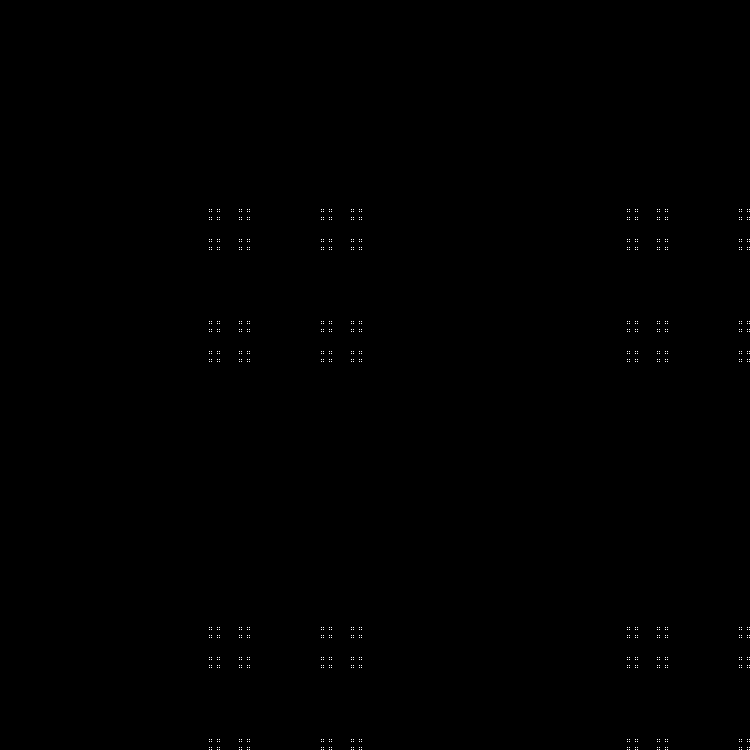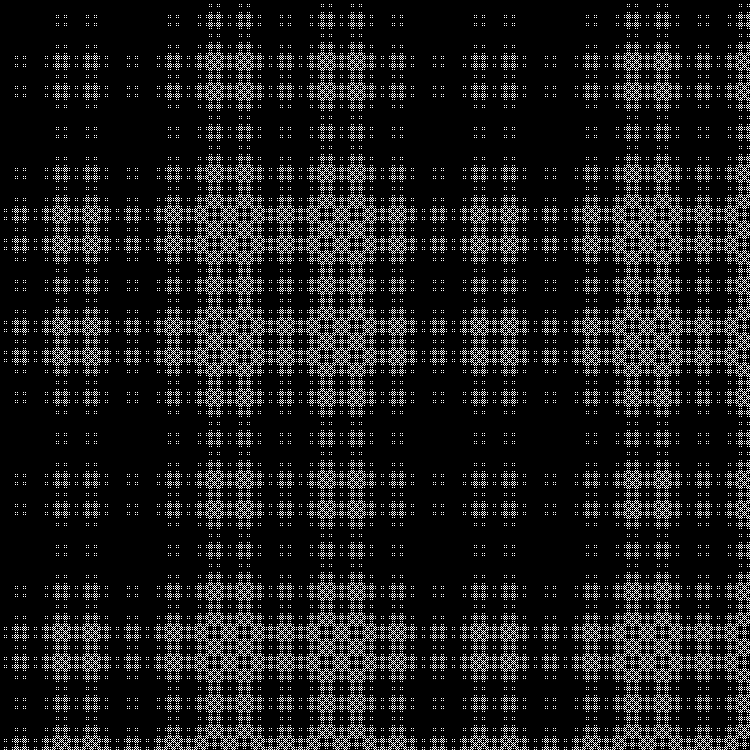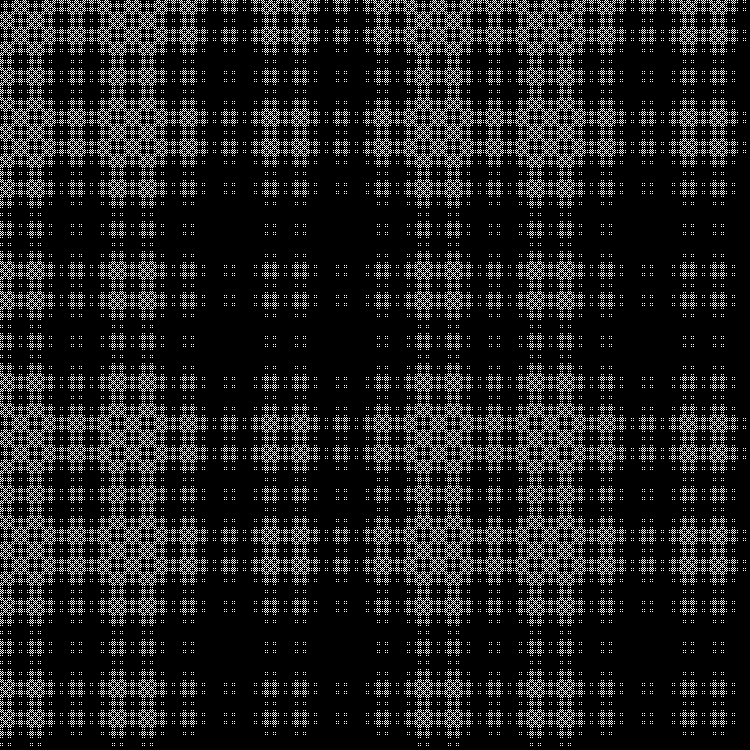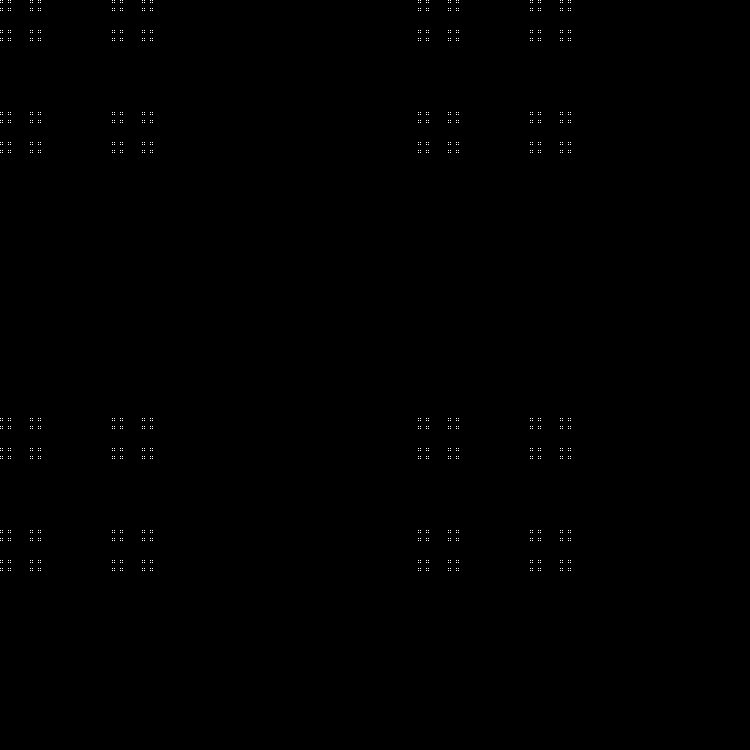
$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Mittlere Schicht:



In der Dynamik:



Nun, unser Lieblingsfraktal (ein Teil dieses Musters kann mit Billard gezeichnet werden, wobei die Seitengrößen den Fibonacci-Zahlen entsprechen):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Mittlere Schicht:



In der Dynamik:



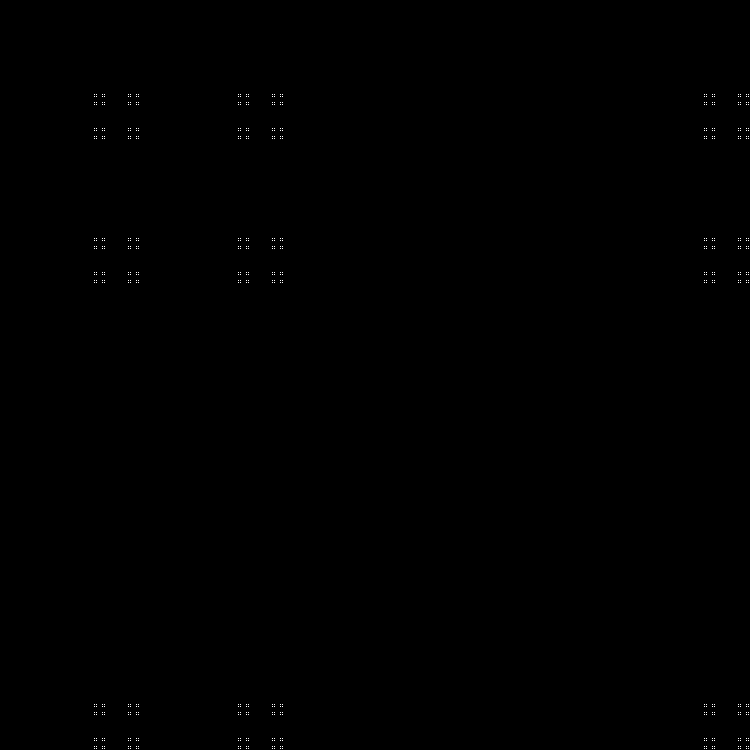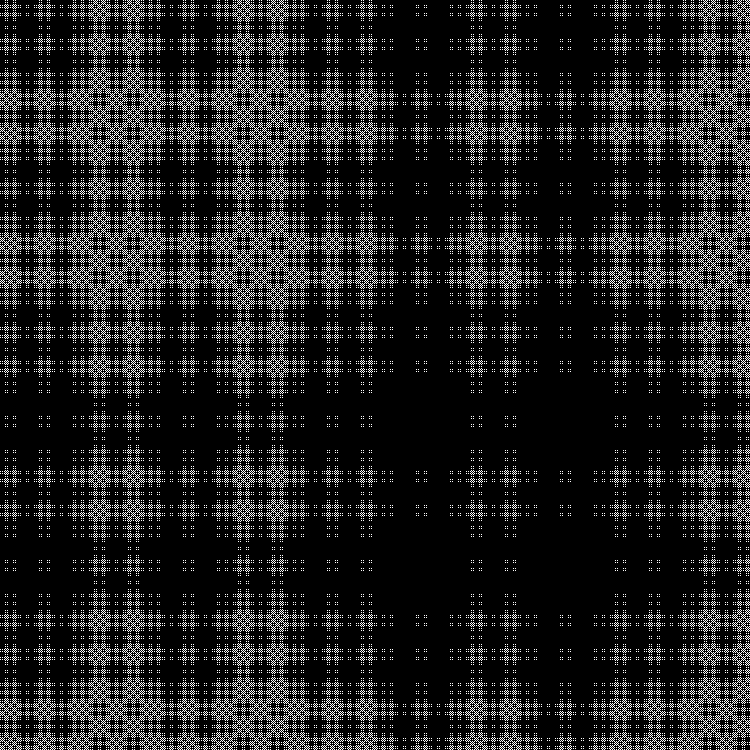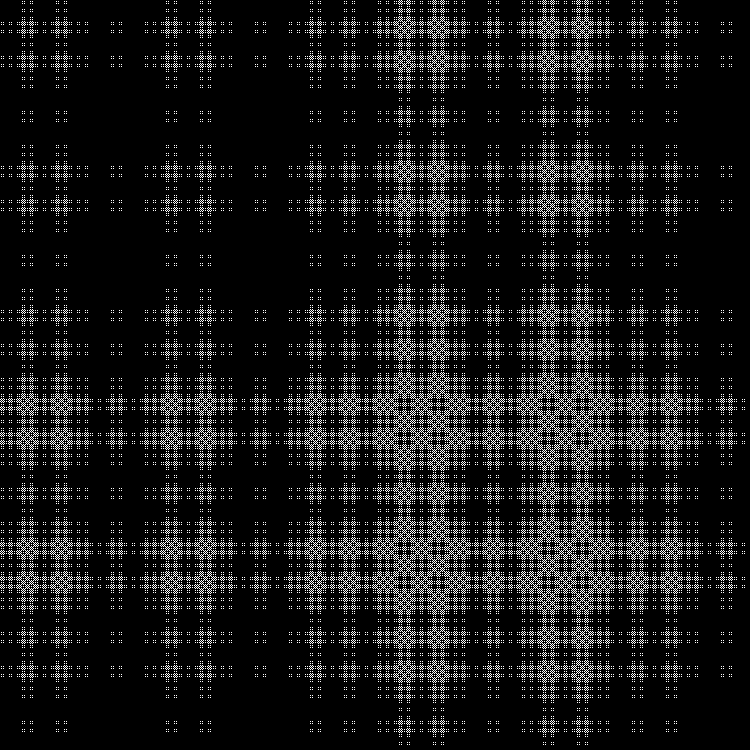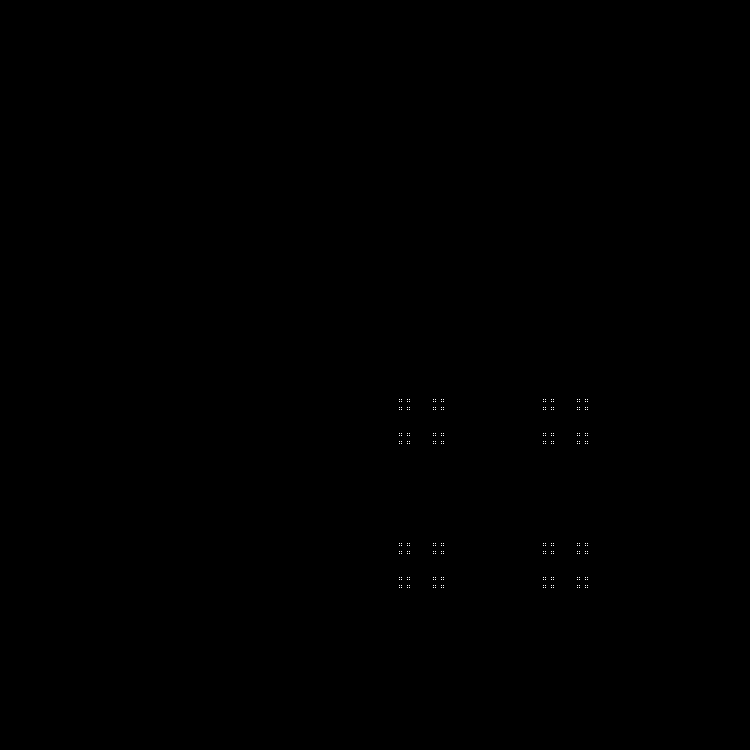
Eine weitere zu vervollständigende Sequenz:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Muster:



RGB:



Mittlere Schicht:



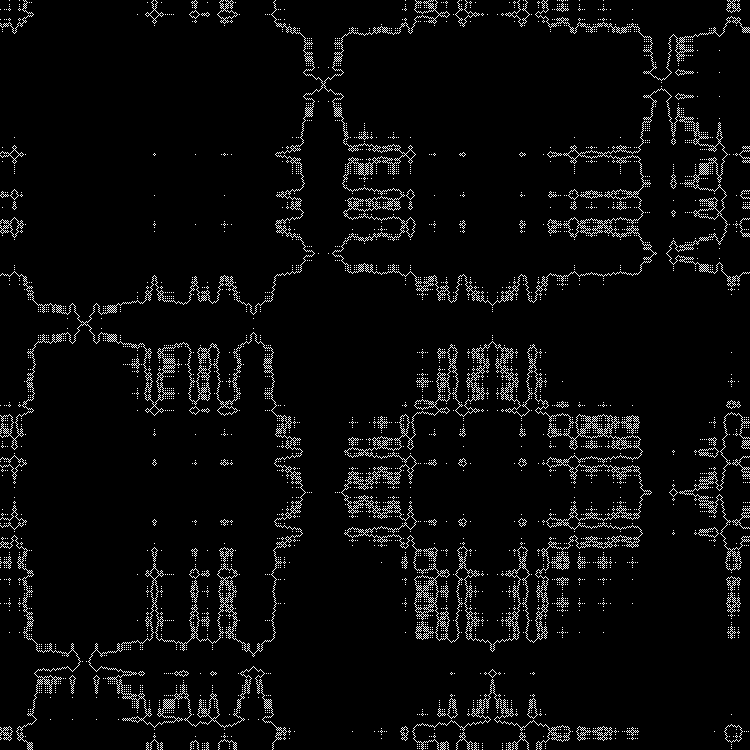
In der Dynamik:



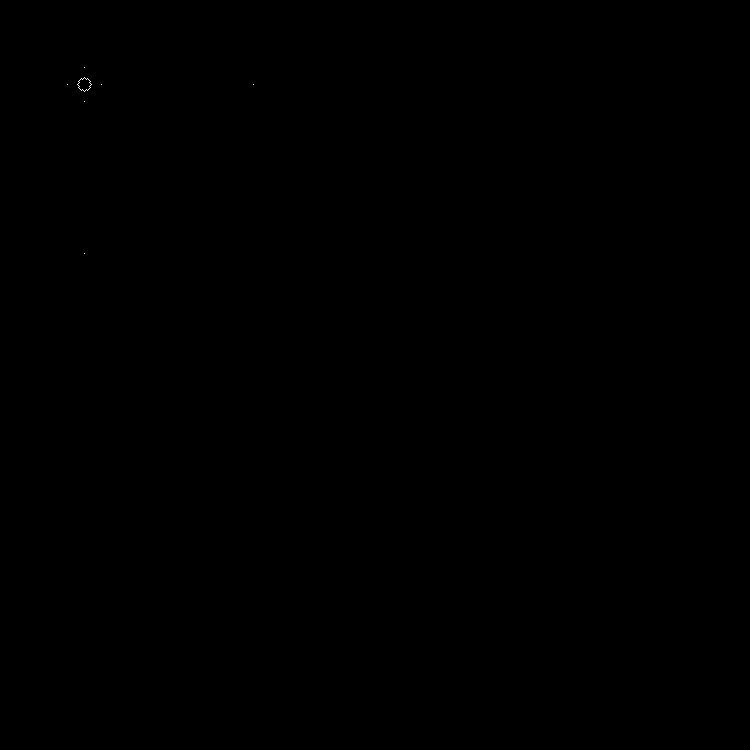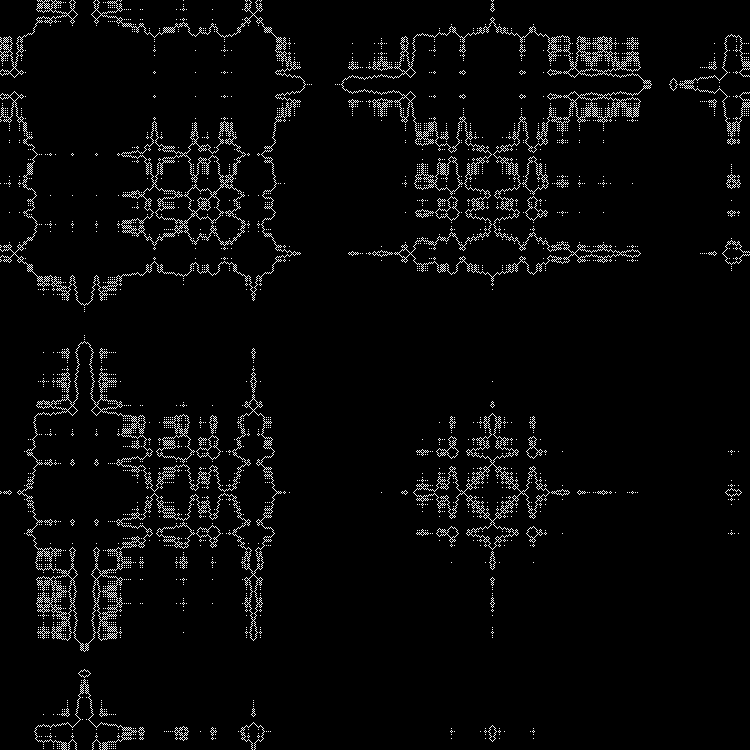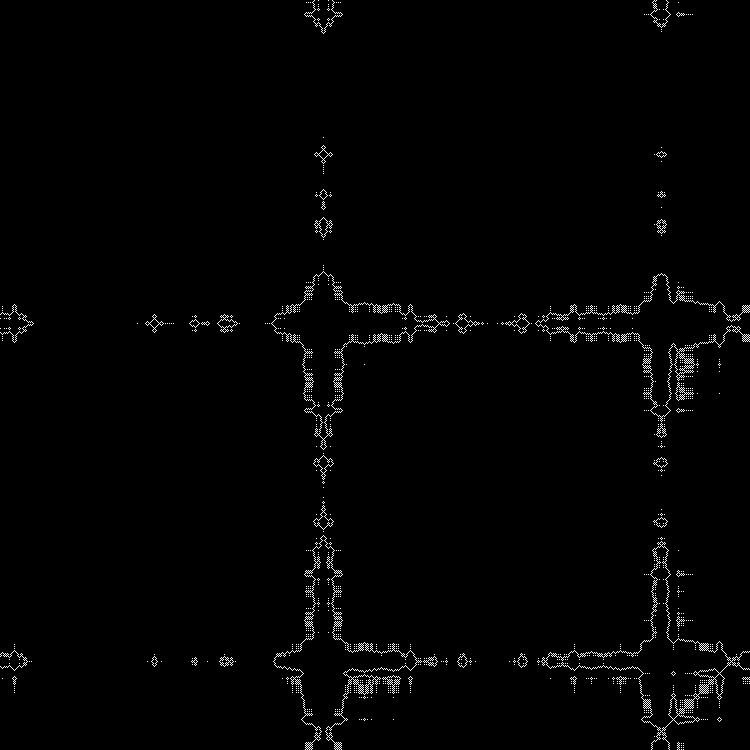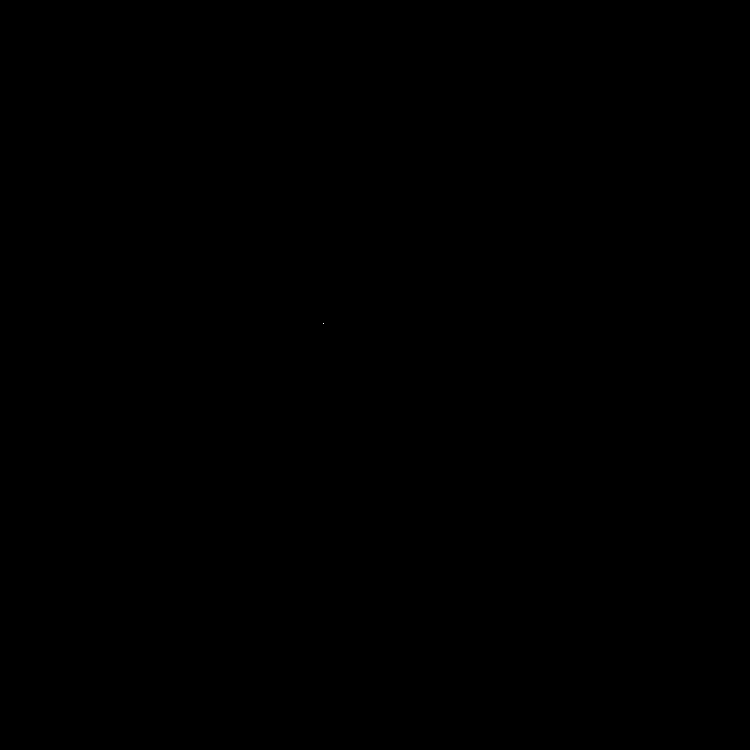
Andere Quadratwurzeln können in das Skript eingefügt werden . (Sie können in Bruchwerten fahren).

Im zweiten Skript können Sie die Sequenz manuell steuern.

Ein weiteres Skript für Billard. Mauskoordinaten - Billardabmessungen. Das Muster auf der linken Seite wird aus der Sequenz gebildet, die unter Verwendung des Restes der Teilung erhalten wurde (Details im vorherigen Artikel). Auf der rechten Seite - Parität $$$\ lfloor n \ frac {y} {x} \ rfloor$ .