Nicht-Mars-Pyramiden: Untersuchung der Form nanokristalliner Cluster unter einer Graphenschicht

Sehr viele Eigenschaften und damit die Methoden zur Verwendung von etwas hängen von der Form dieses Objekts ab. Alles ist sehr einfach und genauso logisch: Runde Räder rollen besser als quadratische Räder, und die Flügel eines Flugzeugs haben eine bestimmte Form, die die Aerodynamik verbessert. Sogar gewöhnliche Stifte haben die Form eines Sechsecks, so dass es bequemer ist, beim Schreiben in der Hand zu halten und nicht in der gesamten Wohnung unter allen Sofas und Schränken in der Pose der Person zu suchen, die Dark Souls zum ersten Mal ins Leben gerufen hat. Das Ändern der Form kann zu einer Änderung der Eigenschaften führen. Wenn diese Änderungen gesteuert werden, können Sie bestimmte Eigenschaften erhalten, die Sie benötigen. Genau das haben Wissenschaftler in der Studie getan, die wir heute betrachten. Sie erstellten ein Modell mit „konstanter Elastizität“ für nanokristalline Kupfercluster unter einer Graphenmembran. Wie und warum haben Wissenschaftler Kupfer mit Graphen „verschmiert“, welche Ergebnisse haben praktische Experimente gezeigt, stimmen sie mit vorläufigen Berechnungen überein und was bedeutet dieses „Sandwich“ im Nanometerbereich für die Wissenschaft? Antworten auf diese Fragen erwarten uns im Bericht der Forschungsgruppe. Lass uns gehen.

Studienbasis

Wie die Wissenschaftler selbst sagen, gibt es nichts Wichtigeres als die Struktur und Form funktioneller Kristalle (Wissenschaftler haben ihre eigenen Lebensprioritäten, wir werden nicht streiten). Während der Synthese dieser kleinen Objekte sind einige Abweichungen von der Gleichgewichtsstruktur möglich, die entweder ein sehr unangenehmes Minus oder ein großes Plus sein können. Wenn Sie die Essenz der Gleichgewichtsstruktur verstehen, können Sie lernen, diese Strukturen besser zu verstehen und sie folglich zu manipulieren.

Eine wichtige Rolle spielen dabei Nanokristalle (NCs), die in mehrere Klassen unterteilt sind: nicht unterstützte dreidimensionale Nanokristalle, die durch Flüssigphasensynthese erhalten wurden, und unterstützte drei- und zweidimensionale Nanokristalle, die durch Abscheidung auf der Substratoberfläche erhalten wurden.

Wenn wir unser Lieblingswort "Quantum" mit all dem verbinden, werden wir Folgendes herausfinden: für Quantenpunkte, d.h. Unterstützt von dreidimensionalen NCs, die durch Gitterfehlanpassung innerhalb der Heteroepitaxie * gebildet werden , spielt die Verformung eine äußerst wichtige Rolle bei der Formkontrolle.

Heteroepitaxie * ist eine Art von Epitaxie (das Wachstum eines kristallinen Materials auf einem anderen bei niedrigen Temperaturen), wenn sich die wachsende Schicht in ihrer chemischen Zusammensetzung vom Substrat unterscheidet.

In dieser Studie betrachten Wissenschaftler einen neuen Typ dreidimensionaler Nanokristalle (Cluster), die sich unter einem Schichtmaterial befinden. Somit werden diese Nanokristalle unter einer oder mehreren Monoschichten (oben) und einer Reihe von semi-infiniten Schichten (unten) komprimiert.

Warum machen Wissenschaftler das, fragen Sie? Sie werden antworten: Der Zweck dieser Studie ist die Entwicklung und Analyse eines Modells konstanter Elastizität (PE), das die Verformungsenergie der oberen Graphenschicht, die Adhäsion und die Oberflächenenergien von Cu (Kupfer), Graphen und Graphit kombiniert und es Ihnen ermöglicht, die Gleichgewichtsform der Oberfläche / eingekapselten Cluster zu steuern .

Den Wissenschaftlern gelang es, ein solches Modell zu erstellen, wonach sie seine Lebensfähigkeit nicht auf Papier, sondern in der Realität testeten. Welche Ergebnisse die Analyse ergab und welche Diskrepanzen zwischen Theorie und Praxis festgestellt wurden, werden wir weiter untersuchen.

Studienvorbereitung

Zu Beginn war es notwendig, Graphit für die Wechselwirkung mit Kupfernanoclustern vorzubereiten. Hierzu wurden durch Beschuss von Ar + Defekte auf seiner Oberfläche erzeugt. Danach kollidierten Cu-Atome mit der Oberfläche von Graphit, drangen in einige Defekte ein und befanden sich bereits unter der Oberfläche von Graphit. Während dieser Aktion wird das Graphitsubstrat auf 600-800 K erhitzt. Dieses Temperaturregime wird aus einem Grund gewählt: Die Cu-Inseln (Cluster) auf der Graphitoberfläche beginnen bei einer Temperatur von 550-600 K zu vergröbern, daher sollte das Aufbrechen der Cu-Cu-Bindung bei 600 leicht erreicht werden sollten K und höher. Infolgedessen bildeten sich in dieser Studie Kupferinseln bei einer Temperatur von 800 K.


Bild Nr. 1

In STM 1a sehen wir nicht die Pyramiden auf der Oberfläche des roten Planeten, sondern genau die Kupferinseln, deren STM-Profil in 1a 'dargestellt ist .

Wissenschaftler lenken unsere Aufmerksamkeit auf die Form dieser Kupferinsel: ein flaches Sechseck. Die Abflachung der Oberseite und dementsprechend der Unterseite zeigt an, dass der zentrale Teil der Insel durch die Substratschicht (unten) und die Graphenschicht (oben) begrenzt ist. Wir sehen auch Hänge, die einen Ring um eine flache Spitze bilden. Beobachtungen zufolge kann die Dicke der Kohlenstoffschicht auf diesen Inseln mehrere Graphenmonoschichten betragen, bis zu drei.

Als nächstes analysierten Wissenschaftler die Form dieser Insel ( 1b ). Es wurde deutlich, dass die Höhe (h) fast identisch mit der Breite des Rings (a) skaliert. Darüber hinaus sind die Steigungen (h / a), dh die Steigung der Seiten, bei verschiedenen Größen konstant. Der Durchmesser skaliert jedoch im Gegensatz zur Breite des Rings schlecht mit der Höhe, dh das Seitenverhältnis d / h ist nicht konstant. Grafik 1c zeigt das Verhältnis von Höhe und Breite des Rings, und Grafik 1d zeigt die Höhe und Breite der Spitze der Insel. Gleichzeitig wurden insgesamt rund 140 Kupferinseln analysiert.

Wie die tatsächliche Situation bei Kupfernanoformationen unter einer Graphenschicht aussieht, ist uns jetzt klar. Nach diesen Beobachtungen erstellten die Wissenschaftler ihr Modell der konstanten Elastizität (PE).

PE-Modell

Bei der Modellierung beschlossen die Wissenschaftler, die Approximation (Approximation) der Form der Kupferinsel anzuwenden, daher wurde die hexagonale Pyramide verwendet, aber die zylindrische. Ein Kupferzylinder wächst zwischen einer Membran aus einer / mehreren Graphenmonoschichten und einem Graphitsubstrat.

Es wird angenommen, dass das Graphitsubstrat starr ist und die Deckschicht (über den Kupferinseln) elastischen Zug- und Biegeverformungen unterliegt, die es ihr ermöglichen, sich an die wachsende Insel anzupassen.

Eine kleine Klarstellung der Begriffe: In Zukunft nennen Wissenschaftler die Inseln in ihrer Arbeit das Aggregat eines Cu-Clusters, einer deformierten Graphenmembran und eines Graphitsubstrats sowie Cluster - nur das zentrale Metallteil.

Ein wichtiges Element der Form der Inseln sind die Hänge der Seiten. Diese Steigungen sind viel kleiner als die der Cu-Ebenen mit niedrigem Index (111) oder (100), die natürlich an die Oberseite (111) des unterstützten Cu-Clusters angrenzen. Daraus folgt, dass der mit Kupfer gefüllte Ringraum aufgrund der Oberfläche mit hohem Index und Oberflächenenergie Cu keine energetisch realisierbare Konfiguration ist.

Ein weiteres wichtiges Merkmal ist das Vorhandensein von Ringfalten, von denen eine in der unteren linken Ecke bei 1a zu sehen ist. Solche Verformungen weisen darauf hin, dass die Membran (Deckschicht) dem Einfluss der Dehnung des darunterliegenden Materials nicht zugänglich ist, wodurch dessen Faltung begrenzt wird.

Die Energie des Systems (Π) kann als die Summe der elastischen Dehnungsenergien des verzerrten Graphenfilms (U _e ) und einer Kombination von Variablen modelliert werden, die die Grenzflächen- und Oberflächenkomponenten (IS - Grenzfläche / Oberfläche) der Gesamtenergie des Systems darstellen. Zu den Grenzflächen und Oberflächen gehören: reines Kupfer, Graphen - Graphit (GnGt), Kupfer - Graphen und Kupfer - Graphit (die Bezeichnung für beide ist CuG). Die folgenden IS-Energien entsprechen den oben genannten:

• Energiekosten im Zusammenhang mit der Oberflächenenergie von Cu, U _Cu und dem Verlust der Haftung Gn - Gt, U _GnGt ;
• Energieverringerung im Zusammenhang mit der Adhäsion von Cu-Gn und Cu-Gt, U _GnGt .

Zusammen werden sie mit dem allgemeinen Begriff U _{IS bezeichnet} . Unten ist die Formel für die Gesamtenergie:

Π = U _Cu + U _GnGt + U _CuG + U _e

Die Gleichgewichtsform wurde durch Minimieren von Π für ein festes Volumen (V) des Cu-Clusters erhalten.

Ferner wurden U _IS , d. H. Grenzflächen- und Oberflächenkomponenten der Gesamtenergie des Systems, berechnet. Jede solche Komponente kann ausgedrückt werden als die Summe der Produkte aus Oberflächenenergie (γ) oder Adhäsionsenergie (β) multipliziert mit der entsprechenden Fläche.


Tabelle Nr. 1: Formeln zur Berechnung von U _IS (links) und Eingabedaten (rechts).

Die Werte von γ und β wurden unter Verwendung der Dichtefunktionaltheorie erhalten. Eine (111) -Orientierung des Cu-Clusters wurde aus experimentellen Daten erhalten.

Anschließend ermittelten die Wissenschaftler den Wert von U _e mithilfe des Berechnungsmodells SLBT (Blistertest mit einem zylindrischen Stab mit flacher Oberseite), bei dem sich der zylindrische Stab durch das Loch in einer festen Oberfläche nach oben bewegt, gegen die elastische Membran drückt und diese verformt.

Die Membran erfährt Zug- und Biegeverformungen. Im SLBT-Modell werden diese beiden Arten der Verformung als unabhängige Beiträge angenähert. Die Berechnungen zeigten, dass die Biegeverformung unter Berücksichtigung der Größe der Versuchsstruktur recht gering ist, so dass die Modellierung der gesamten elastischen Membranenergie (U _e ) nur unter Berücksichtigung der Zugspannung möglich war.

Der Ringraum kann uneingeschränkt auf das Inselwachstum reagieren, aber die Haftung zwischen dem Teil des Graphens oben auf der Insel und Kupfer kann eine seitliche Ausdehnung des Graphens verhindern. Wenn die Dehnung frei verläuft, kann sich dieser Teil auch über der Oberseite der Insel frei verformen.

Aufgrund dieser Aussage wurde die Formel U _e abgeleitet (Nr. 5 in Tabelle 1). Daraus können wir verstehen, dass der Wert von U _e vom Poisson-Verhältnis (v), dem Längselastizitätsmodul (Y) und der Dicke von Graphen (t) abhängt. Der Wert von v betrug 0,165, Y - 1,1 TPa, da dies den experimentellen Werten der Defektdichte (7,3 ± 0,4) × 10 ³ & mgr; m ^{–2 entspricht} .

In Bezug auf die Dicke von Graphen wissen wir bereits, dass Graphen auf Inseln mehr als eine Monoschicht dick sein kann. Dies ermöglicht es uns, die Dicke der oberen Schicht der untersuchten Struktur unter Verwendung der Formel t = L · t _GML zu berechnen, wobei L die Anzahl der Graphenschichten und t _GML 0,34 nm ist (Zwischenschichtabstand in kristallinem Graphit).

Forschungsergebnisse

Und so. Wenn die Beobachtungsdaten aussortiert sind und auch der Berechnungsteil, ist es Zeit, die Ergebnisse der Analyse all dessen insgesamt zu beginnen.

Mit den Formeln U _IS und U _e sowie den Daten aus Tabelle 1 (rechts) wird Π zu einer Funktion von nur drei unabhängigen Parametern - a, h und d. Dieses Problem kann gelöst werden, indem der Clustervolumenwert V = πhd 2/4 genau eingestellt wird, wodurch wir entweder h oder d eliminieren können. Somit werden nur zwei Parameter erhalten und nicht drei: Π = Π (a, h) oder Π = Π (a, d). Für die Demonstration verwendeten die Wissenschaftler Π (a, h), und das Clustervolumen wurde aus den verwendeten Daten entnommen - _exp V _exp 〉 = ⁴ × ^{10 4} nm ³ (Bild Nr. 2).


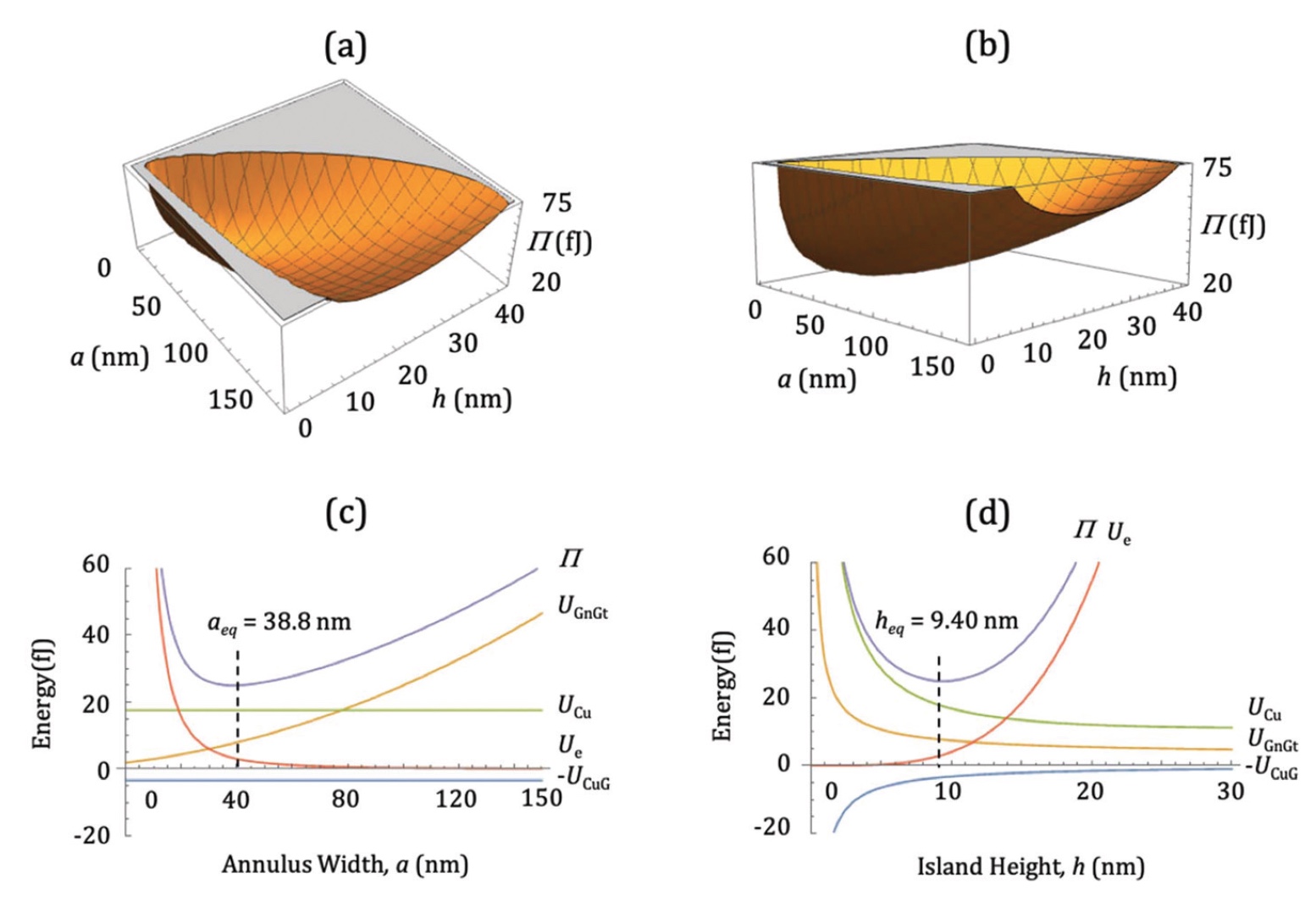Bild Nr. 2

Wissenschaftler bemerken einen äußerst wichtigen Punkt: Es gibt einen bestimmten Mindestwert von Π, der ein Gleichgewichtszustand ist. Mit einem solchen Minimum sagt das Modell der konstanten Elastizität die folgenden Werte voraus: a _Gleichung = 38,8 nm, h _Gleichung = 9,4 nm und d _Gleichung = 73,6 nm. In den Experimenten hatten die Inseln, die in Bezug auf V _exp nahe beieinander lagen, die folgenden Parameter: a _exp = 31 ± 11 nm, h _exp = 7,3 ± 2,6 nm und d _exp = 88 ± 21 nm. Wie wir sehen können, stimmen die theoretischen und praktischen Daten sehr gut überein.

Die Graphen 2c und 2d zeigen zwei orthogonale Schnitte durch Π (a, h), von denen jeder ein globales Minimum durchläuft.

Die obigen Prozesse können über den gesamten Bereich experimentell beobachteter Clustervolumina (1,8 × 10 ³ nm ³ ≤ V ≤ 6,9 × ^{5 5} nm ³ ) wiederholt werden. Daher ist es möglich, die vom Modell vorhergesagten und in Experimenten beobachteten Inselgrößen zu vergleichen. Für einen einfacheren Vergleich von Modell und Experiment wird das Verhältnis der Größen der Inseln und des Wertes von h verwendet (Bild Nr. 3).


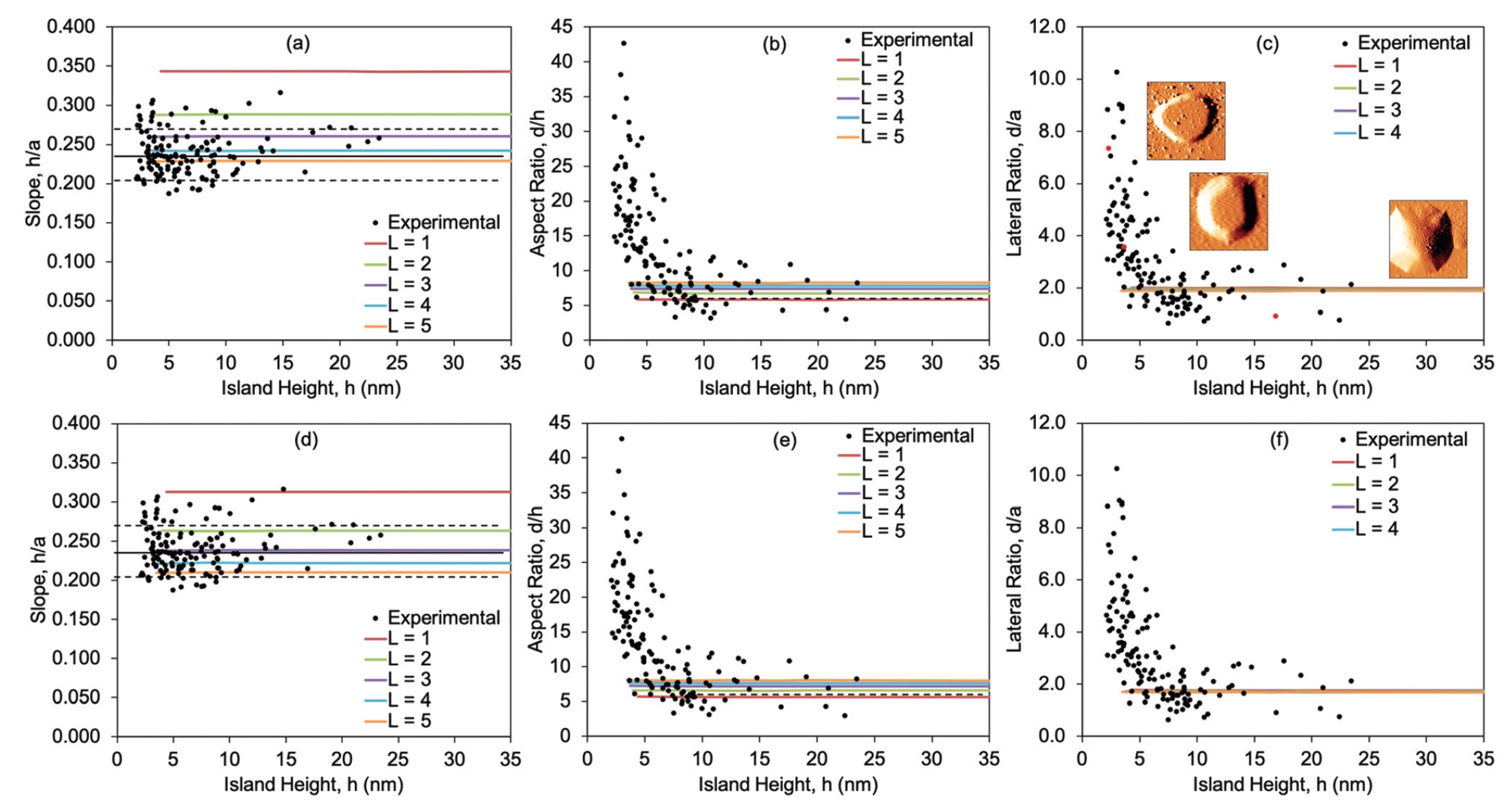Bild Nr. 3

Die obigen Grafiken zeigen h / a, d / h und d / a sowohl für das Modell als auch für das Experiment. Die Diagramme 3a - 3c sind ein Vergleich der experimentellen Daten und des SLBT-Modells, bei dem die Membranexpansion ohne Einschränkungen verläuft, und 3d - 3f sind bereits experimentelle Daten und ein Modell mit begrenzter Expansion.

Der h / a-Wert in den Experimenten ist konstant und beträgt im gesamten Bereich der Inselgrößen 0,24 ± 0,03. Theoretisch wurde das Volumen der Cluster 1 ≤ L ≤ 5 verwendet, und die beste Übereinstimmung zwischen den Indikatoren von Theorie und Praxis wurde bei L = 4 gefunden.

Beim Wert von d / h (und parallel zu d / a) werden ungewöhnliche Änderungen beobachtet. Wie aus Grafik 3b ersichtlich ist, beginnt der experimentelle Wert von d / h bei 40, beginnt dann aber mit zunehmendem Wert von h stark abzunehmen. Wenn h ≤ 10 nm erreicht, wird der d / h-Wert auf 7,3 ± 2,8 ausgeglichen (horizontale gestrichelte Linie bei 3b). Das theoretische Modell zeigte d / h-Werte im Bereich von 5,6 bis 8,0 für L = 1 ... 5.

Bei einem festen SLBT-Modell ist die Leistung dem kostenlosen SLBT-Modell sehr ähnlich. Der einzige signifikante Unterschied besteht darin, dass für jeden Wert von L das h / a-Verhältnis im festen Modell etwas geringer ist als im freien Modell. Somit zeigt sich die beste Übereinstimmung zwischen Theorie und Praxis bei einem festen SLBT-Modell bei L = 3.

Für eine detailliertere Untersuchung der Studie empfehle ich dringend, dass Sie sich den Bericht der Forschungsgruppe ansehen.

Nachwort

Was haben wir gemeinsam? Wissenschaftler haben ein theoretisches Modell erstellt, das hervorragend mit experimentellen Daten übereinstimmt. Dieses Modell zeigt, dass die Form von nanokristallinen Kupferclustern zumindest bei Skalen, bei denen die Biegebeanspruchung nicht sehr stark ist, bestehen bleibt. Die Forscher fanden auch heraus, dass die Delaminierung im Ringraum eine Reaktion auf die Verschiebung der Membran (Deckschicht) ausschließlich im zentralen Bereich (dem Innenumfang des Rings) ist und die Eigenschaften von Graphen / Graphit und nicht von Kupfer selbst widerspiegelt.

Darüber hinaus wurde festgestellt, dass ähnliche oben beschriebene Beobachtungen für Systeme gelten, in denen ein Metallcluster nahe der Oberfläche eines dreidimensionalen Schichtmaterials oder unter einer getragenen zweidimensionalen Membran eingebettet ist, jedoch nur unter der Bedingung einer Gleichgewichtsform. In diesem Fall ist es notwendig (und möglicherweise, wie die Ergebnisse zeigten), die mechanischen Eigenschaften der Membran, die Adhäsion und die Oberflächenenergien zu verwenden, um die Gleichgewichtsform des eingekapselten Körpers, d. H. Metallcluster (in dieser Arbeit Kupfer), vorherzusagen. Dieses Prinzip funktioniert auch in die entgegengesetzte Richtung - man kann die Energie und die mechanischen Eigenschaften durch Messen der Clustergrößen herausfinden. Wissenschaftler geben ein kurzes Beispiel: Durch Messen von h und a und Kenntnis der mechanischen Eigenschaften der Membran ist es möglich, die Adhäsionsenergie des Membransubstrats zu bestimmen.

Diese Arbeit kann am besten in modernen Technologien verwendet werden, die auf Schichtmaterialien beruhen - Graphit oder seinen Derivaten wie Graphen. Und wenn wir berücksichtigen, dass die Tendenz zu einer Verringerung der physikalischen Abmessungen elektronischer Geräte noch nicht abnimmt, dann haben solche Studien einen hohen Preis, und deshalb werden wir auf neue schockierende Entdeckungen und erstaunliche Experimente warten.

Vielen Dank für Ihre Aufmerksamkeit, bleiben Sie neugierig und haben Sie eine gute Arbeitswoche, Jungs!

Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Ihren Freunden empfehlen, einen Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).

VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s bis zum Sommer kostenlos, wenn Sie für einen Zeitraum von sechs Monaten bezahlen, können Sie hier bestellen.

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel Dodeca-Core Xeon E5-2650v4 128 GB DDR4 6 x 480 GB SSD 1 Gbit / s 100 TV von 249 US-Dollar in den Niederlanden und den USA! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?