Einführung

Über das Projekt

Das Projekt „Absoluter Wechselkurs“ befasst sich mit der Analyse gepaarter Wechselkurse, der Allokation absoluter Wechselkurse und deren Analyse. Im Rahmen des Projekts wurde eine Methode zur Umrechnung von Paarkursen in absolute Wechselkurse erhalten. Hierzu wird die absolute Währung ABS definiert. Alle verfügbaren Währungen werden in ABS ausgedrückt.

Eine ausführliche Beschreibung der Technologie finden Sie im Artikel „Von Währungspaaren zu absoluten Wechselkursen“ .

Über das Problem

Dieser Artikel befasst sich mit dem Problem einer qualitativen Analyse der Kohärenz von Wechselkursen.
Die Notwendigkeit, die Beziehung zwischen Währungen zu untersuchen, beruht auf den Anforderungen für die Auswahl von Finanzinstrumenten im Anlageportfolio und der Fähigkeit, das Verhalten von Währungen anhand von Daten zu anderen damit verbundenen Währungen vorherzusagen.

Es ist ratsam, Instrumente mit hoher multidirektionaler Konnektivität in das Anlageportfolio aufzunehmen. Dies reduziert das Gesamtrisiko des Portfolios.

Und wenn Sie Tools mit einem hohen Grad an Verbundenheit finden, können Sie anhand des Verhaltens einiger das Verhalten anderer vorhersagen.

Über das Experiment

Methodenauswahl

Als Ausgangsdaten für das Experiment gibt es Datenreihen mit absoluten Wechselkursen (siehe Quelldatei. Blatt „Absolute Wechselkurse“ ).



Um die Konnektivität einer Reihe numerischer Daten zu untersuchen, verwenden Sie am besten die Pearson-Korrelation (siehe Korrelation - Wikipedia ).

Der Korrelationskoeffizient hat einen Wertebereich von "-1" bis "+1". Große negative Werte weisen auf eine starke multidirektionale Beziehung hin. Große positive Werte zeigen eine starke unidirektionale Konnektivität an. Die Nähe des Koeffizienten zu „0“ zeigt das Fehlen einer Kommunikation an.

Was willst du bekommen?

Der Zweck des Experiments besteht darin, Währungsgruppen mit einem hohen Grad an Verbundenheit zu erhalten. Darüber hinaus ist auch das Zeichen der Kommunikation von Interesse.

Veranstaltungort

Alle Berechnungen werden im Wolfram Mathematica-System durchgeführt (siehe Wolfram Mathematica - Wikipedia ). Und wir werden Wolfram.Cloud kostenlose Cloud-Ressourcen verwenden.

Mit der angegebenen Ressource können Sie Online-Notizbücher mit Berechnungen erstellen und Zugriff für die allgemeine Anzeige gewähren. Das Notizbuch dieses Experiments befindet sich hier .

Planen

Wir werden Berechnungen nach folgendem Plan durchführen.

Zuerst berechnen wir die Korrelationsmatrix. Spalten und Zeilen der Matrix entsprechen den einzelnen Währungen. Am Schnittpunkt von Spalte und Zeile befindet sich der Paarkorrelationskoeffizient.

Als nächstes wählen wir Währungspaare mit den stärksten Bindungen aus. Platzieren Sie die ausgewählten Paare in der Grafik (siehe Grafik (Mathematik) - Wikipedia ).

Die Knoten des Diagramms sind Währungen. Die Kanten des Diagramms zeigen die Beziehung zwischen den Währungen an. Die Farbe der Rippe zeigt das Bindungszeichen an. Grün zeigt eine positive Beziehung an und Rot zeigt eine negative Beziehung an.

Die angegebene Abfolge von Berechnungen wird sowohl für absolute Kurse als auch für deren Änderungen durchgeführt. Eine Analyse der Beziehung zwischen absoluten Kursen ermöglicht es Ihnen, langsame Prozesse (mehr als einen Tag) zu untersuchen. Eine Analyse der Beziehung zwischen Änderungen der absoluten Wechselkurse ermöglicht es uns, die schnellen Verbindungen zwischen Währungen (eines Tages) zu untersuchen.

Ergebnisse

Probentiefe

Die Quelldatei enthält Daten der letzten 150 Tage. Demnach wird die Berechnung durchgeführt.

Währungswolke

Das Experiment umfasste 45 Währungen.



Eine vollständige Liste der Währungen finden Sie auf dem Blatt „Währungsübersicht“ der Quelldatei .

Absolute Ratenkorrelation

Oben (siehe Plan) war geplant, die Korrelationsmatrix für absolute Raten zu berechnen. Das Ergebnis ist in der Abbildung unten dargestellt.



Hier entspricht Rot einer positiven Verbindung und Blau einer negativen. Zum Verständnis wird eine Abstufungsskala angegeben. Unten und links befinden sich die Währungsticker (Kurznamen).

Diagramm der absoluten Ratenabhängigkeit

Die Korrelationsmatrix ermöglichte die Unterscheidung von zwei Währungsgruppen mit einem hohen Grad an Verbundenheit. Dazu wurden Paare mit einer Korrelation von mehr als 0,9 ausgewählt und in den Graphen übertragen.



Die erste Gruppe sammelte Währungen mit einer hohen Abhängigkeit vom US-Dollar. Hier sind die Währungen von vier arabischen Ländern, die mit Öl handeln, dem Hongkong-Dollar und dem US-Dollar selbst. Alle Abhängigkeiten sind positiv (unidirektional).

Die zweite Gruppe sammelte europäische Währungen. Im Zentrum steht der Euro selbst und um ihn herum die Währungen Polens, Rumäniens und Dänemarks. Alle Abhängigkeiten sind positiv (unidirektional).

Relative Änderungen der absoluten Raten

Für weitere Untersuchungen haben wir die Reihe der relativen Änderungen der absoluten Raten berechnet. Die Formel für die Berechnungen lautet wie folgt.



Die Differenz zwischen aufeinanderfolgenden Werten wird mit dem früheren der beiden korreliert. Somit erhalten wir eine relative Änderung der absoluten Rate.

Korrelation der relativen Änderungen der absoluten Raten

Für absolute Kurse erhalten wir eine Korrelationsmatrix für relative Messungen von absoluten Kursen. Wir geben eine grafische Darstellung der Matrix.



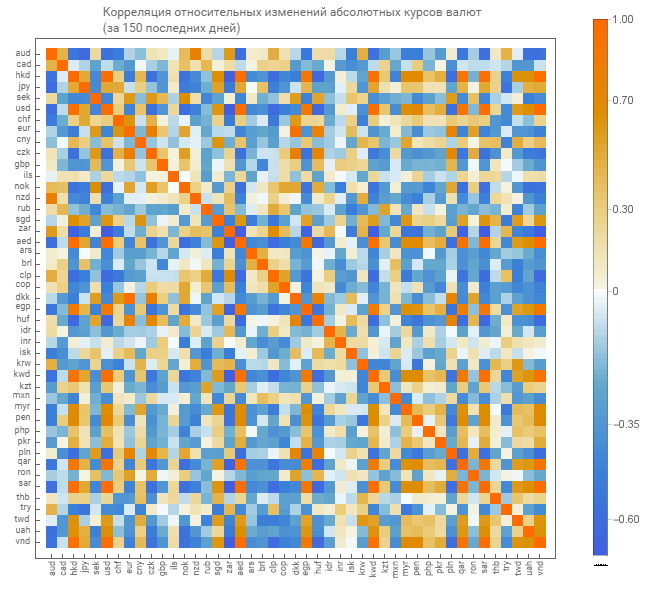
Es gibt bereits eine Matrix hellerer Töne. Was auf einen geringeren Grad an Verbundenheit hinweist.

Abhängigkeitsdiagramm der relativen Änderungen der absoluten Raten

Aus der Korrelationsmatrix der relativen Änderungen wählen wir Währungspaare mit einem hohen Grad an Verbundenheit aus. Nur der Stichprobenpegel beträgt hier bereits 0,6 (hier und darüber wurde dieser Koeffizient aus der Berücksichtigung einer kleinen Anzahl von Paaren für die Ausgabe in den Graphen ausgewählt).



Bei relativen Veränderungen erhielten 3 Währungsgruppen. Die obere Gruppe kombinierte die Währungen von Australien und Neuseeland. Die untere Gruppe sammelte europäische Währungen. Die mittlere Gruppe um den Hongkong-Dollar kombinierte die Währungen der USA, Vietnams, fünf arabischer Länder - Ölexporteure, Südafrika und Peru.

Darüber hinaus gibt es ein interessantes Merkmal in der hohen negativen Abhängigkeit vom südafrikanischen Rand.

Schlussfolgerungen

Als Ergebnis des Experiments gelang es uns, Folgendes zu erhalten.

Das Einfügen der Korrelationsmatrixdaten in einen mathematischen Graphen ist eine gute Visualisierungspraxis für die Korrelationsmatrix. Eine weitere Anwendung dieser Methode vereinfacht das Verständnis der Beziehungen in der Gruppe der Zahlenreihen.

Es wird eine formale Methode zur Clusterbildung von Devisenmärkten gefunden. Es war möglich, die Märkte Europas, Amerikas mit Asien und Ozeanien formal zu unterscheiden. Diese Methode kann den Weg zur Aufdeckung der gegenseitigen Einflüsse zwischen den Märkten verschiedener Länder erheblich verkürzen und ein gutes Instrument für einen Finanzanalysten werden.

Die Aufnahme des südafrikanischen Rand in das Anlageportfolio zusammen mit dem US-Dollar wird die Risiken eines solchen Portfolios verringern.

Katalog der Artikel