Eine universelle Methode zur Lösung von Problemen am Beispiel des Puzzles "12 Münzen, 3 Wägungen"

Bei der Lösung hilft es:

1) Abnahme der Entropie (Maß für die Unsicherheit) und Antworten auf Fragen:

• Was haben Sie im vorherigen Schritt gelernt?
• Was reduziert die Unsicherheit?
• Welche Informationen haben wir?
• Was müssen Sie noch wissen?

Fragen sind für jede Aufgabe, jedes Projekt geeignet. Antworten auf diese Fragen tragen dazu bei, das Risiko zu verringern, dass Fristen nicht eingehalten werden, das Budget überschritten wird und die Vorgesetzten aufholen.

2) Zersetzung. Der Ansatz von einfach bis komplex. Wenn Sie eine Lösung für die einfachsten Fälle vorbereiten und diese dann zur Lösung des Problems verwenden (den Algorithmus teilen und erobern), ist dies einfacher, als die gesamte Situation in Ihrem Kopf darzustellen.

Die Divide- und Conquer-Algorithmen unterteilen eine Aufgabe in zwei oder mehr Unteraufgaben desselben Typs, die jedoch kleiner als elementare Aufgaben sind, und kombinieren ihre Lösungen, um eine Antwort auf das ursprüngliche Problem zu erhalten.

Stellen Sie Fragen zur Zersetzung. Welches würdest du vorschlagen?

Welche Fragen haben Sie zur Zersetzung formuliert? Irgendwelche Übereinstimmungen?

1) Was ist die elementarste Situation? Was können wir in einem Wägen tun?

Bei einer Wägung können wir feststellen, welche Münze schwerer ist, ob das Gewicht der Münzen gleich ist.

2) Wenn wir 2 Münzen haben und, wie Sie wissen, Fälschungen härter oder leichter sind. Wie kann man eine Fälschung in einem Gewicht bestimmen?

Es ist notwendig, die Münzen zu wiegen und abhängig vom Pfeil der Waage die Fälschung zu bestimmen.

3) Wenn wir 2 Münzen haben und es nicht bekannt ist, dass Fälschungen schwieriger oder einfacher sind, wie kann man Fälschungen in einem Gewicht bestimmen?

Nach dem Wiegen einer der 2 präsentierten Münzen mit der dritten Münze, über die bekannt ist, dass es sich um eine echte handelt.

4) Wenn wir 3 Münzen haben und, wie Sie wissen, Fälschung härter oder leichter ist. Wie kann man eine Fälschung in einem Gewicht bestimmen?

Es ist notwendig, zwei dieser Münzen zu vergleichen. Wenn sie gleich sind, ist die dritte Münze falsch.

5) Wenn wir 3 Münzen haben und es unbekannt ist, ist Fälschung schwieriger oder einfacher. Ist es möglich, eine Fälschung in einem Gewicht zu bestimmen?

Leider gibt es keine.

6) Wenn wir 4 Münzen haben und unbekannte Fälschungen härter oder leichter sind, können wir die Fälschung in einem Wiegen bestimmen?

Leider gibt es keine.

7) Wenn wir 4 Münzen haben und es nicht bekannt ist, dass Fälschung härter oder leichter ist, wie viele Wägungen können Sie Fälschung bestimmen?

Für zwei Wägungen.

Als nächstes sammeln wir aus elementaren Fällen Situationen von 8, 9, 10, 11 und 12 Münzen. Wie sehen Sie die Lösung?

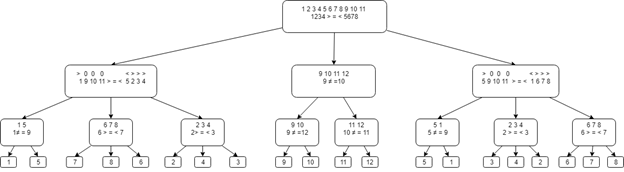
Unten finden Sie die vollständige Lösung.

Erster Schritt: Teilen Sie die Münzen in 3 Gruppen zu je 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.

Vergleichen Sie die ersten beiden Gruppen. Drei Optionen sind möglich:

1. die erste Gruppe ist schwerer;
2. die zweite Gruppe ist schwerer;
3. sind gleich.

1) Wenn die Gruppen gleich sind, befindet sich die gefälschte Münze in der dritten Gruppe. Es ist notwendig, eine gefälschte Münze mit 4 Münzen in zwei Wägungen zu finden.



Teilen Sie die dritte Gruppe in zwei Teile: 9 10 11 12

Vergleiche 9 und 10:

• Wenn sie gleich sind, dann die gefälschte Münze in der zweiten Gruppe - vergleiche 9 und 11. Wenn 9 und 11 gleich sind, dann die gefälschte - 12, wenn nicht -11
• Wenn sie nicht gleich sind, dann falsch in der ersten Gruppe - vergleiche 10 und 12. Wenn 10 und 12 gleich sind - falsch - 9, wenn nicht - 10.

Also haben wir eine gefälschte Münze gefunden.

2) Betrachten Sie den zweiten Fall. Wenn die erste Gruppe schwerer als die zweite ist, weisen wir der ersten Gruppe das Zeichen ">", der zweiten Gruppe das Zeichen "<" und der dritten Gruppe das Zeichen "0" zu.



Wir teilen die Münzen in die gewogenen Gruppen 1 9 10 11 und 5 2 3 4 ein. Drei Optionen sind möglich:

• Sind gleich. Die gefälschte Münze gehört zu den Zahlen: 6 7 8. Vergleichen Sie 6 und 7, wenn sie gleich sind, ist die Fälschung 8, wenn 6 größer ist, die Fälschung - 7, wenn 7 größer ist, die Fälschung - 6, da in diesem Fall die gefälschte Münze einfacher ist.
• Die erste Gruppe ist schwerer, dann ist die gefälschte Münze entweder 1 oder 5. Vergleichen Sie 1 und 9, wenn sie gleich sind - die gefälschte Münze - 5, wenn nicht - 1.
• Die erste Gruppe ist einfacher, dann Fälschung unter den Münzen 2 3 4, da bekannt ist, dass 9, 10 und 11 echt sind, und die zweite Gruppe nur durch die Münzen 2, 3 und 4 aufgewogen werden kann. Vergleichen Sie 2 und 3, wenn sie gleich sind, Fälschung 4, Wenn 2 schwerer ist, ist Fake 2, andernfalls ist 3rd Fake.

3) Der Fall, in dem die zweite Gruppe schwerer als die erste ist, ähnelt der zweiten.


Das allgemeine Diagramm des Entscheidungsbaums ist unten dargestellt.

Wenn eine Aufgabe zur Überarbeitung oder zum Debuggen eintrifft, empfiehlt es sich, den obigen Ansatz anzuwenden:

1. Entscheiden Sie, was gegeben wird?
2. Welche elementaren Fälle / Aufgaben können zerlegt werden?
3. Was ist unbekannt, um das Problem zu lösen? Welche Experimente müssen durchgeführt werden, um die Entropie zu reduzieren?
4. Ausführen.
5. Ist das Problem gelöst? Nein? Kehren Sie zu Schritt 1 zurück.

Erfolgreiche Lösungen.